泡利矩阵(一)
〇、厄米矩阵
厄米矩阵(Hermitian Matrix),也称为自共轭矩阵(Self-adjoint Matrix),是线性代数中的一个重要概念。它是指一个复数域上的方阵,其转置矩阵与共轭矩阵相等。
具体来说,设A为一个n×n的复数矩阵,如果满足A的转置矩阵A等于A的共轭矩阵A*,即A^T = A*,则矩阵A被称为厄米矩阵。
换句话说,厄米矩阵的每个元素a_ij满足两个条件:
- 共轭对称性:a_ij = a_ji*,即矩阵元素关于主对角线对称,并且共轭关系成立。
- 实数性:对于主对角线上的元素,a_ii = a_ii*,即主对角线上的元素是实数。
厄米矩阵在量子力学和数学物理等领域中具有重要的应用。在量子力学中,厄米矩阵用于描述量子系统的物理量(如能量、角动量等)的观测值。厄米矩阵的性质保证了它的特征值都是实数,且对应的特征向量是正交的(由两个不等的特征值保证),这与量子力学中观测物理量时的实验结果相符。
厄米矩阵还具有一些重要的性质,例如它的特征值都是实数、它可以对角化为实对角矩阵、它的特征向量可以构成(施密特正交化)一组正交完备的基等。
总结来说,厄米矩阵是一种特殊的复数方阵,具有共轭对称性和实数性质,它在量子力学和数学物理等领域中扮演着重要的角色。
一、酉矩阵或幺正矩阵
幺正矩阵(Unitary Matrix)是线性代数中的一个重要概念,它是指一个复数域上的方阵,其共轭转置矩阵与逆矩阵相等,也称为酉矩阵。
具体来说,设U为一个n×n的复数矩阵,如果满足U的共轭转置矩阵U†等于U的逆矩阵U(-1),即U^† = U^(-1),则矩阵U被称为幺正矩阵。
换句话说,幺正矩阵的每个元素u_ij满足两个条件:
- 单位正交性:U^†U = UU^† = I,其中I是单位矩阵。
- 行列式模长为1:|det(U)| = 1,即幺正矩阵的行列式的模长等于1。
幺正矩阵在量子力学和数学物理等领域中具有重要的应用。在量子力学中,幺正矩阵用于描述量子系统的幺正演化,它保持向量的内积和模长不变,从而保持量子态的归一性和相对相位关系。幺正矩阵也用于描述量子门操作,即量子计算中的基本逻辑门,如Hadamard门、CNOT门等。
幺正矩阵还具有一些重要的性质,例如它的特征值的模长都等于1,它可以对角化为对角矩阵,且其特征向量构成一组正交完备的基等。
总结来说,幺正矩阵是一种特殊的复数方阵,具有单位正交性和行列式模长为1的性质。它在量子力学和数学物理中被广泛应用,用于描述量子系统的演化和操作。
二、幺正矩阵的性质
酉矩阵(Unitary Matrix)具有许多重要的性质,这些性质在线性代数和量子力学中起着关键的作用。以下是酉矩阵的主要性质:
-
正交性:酉矩阵的转置矩阵和共轭矩阵相等,即U^† = U^T。这意味着酉矩阵的每一列都是一个单位向量且两两正交。
-
逆矩阵:酉矩阵的逆矩阵也是酉矩阵,即U†的逆矩阵等于U,即(U†)^(-1) = U。
-
行列式性质:酉矩阵的行列式的模长等于1,即|det(U)| = 1。这意味着酉矩阵保持了线性空间的体积。
-
特征值性质:酉矩阵的特征值的模长都等于1。这表示酉矩阵的特征值处于复数单位圆上,它们对应的特征向量是正交的。
-
对角化:任何一个n×n的酉矩阵都可以对角化为一个对角矩阵,其对角线上的元素都是复数单位模长为1的特征值。
-
内积保持:对于两个向量x和y,酉矩阵U保持它们的内积不变,即(x, y) = (Ux, Uy)。
-
幺正演化:酉矩阵用于描述量子系统的幺正演化,保持量子态的归一性和相对相位关系。
这些性质使得酉矩阵在量子力学中具有重要的应用。酉矩阵用于描述量子系统的演化和操作,例如量子门操作和量子态的变换。在量子计算和量子信息领域,酉矩阵被广泛应用于量子电路设计和量子算法的实现。
三、张量
张量(Tensor)是线性代数和多线性代数中的一个重要概念,用于描述多维数组的扩展。在一维情况下,张量可以被视为向量。然而,在更高维度的情况下,张量可以具有更复杂的结构。
形式上,一个r阶张量可以表示为一个具有r个指标的多维数组,每个指标对应于一个维度。每个维度可以具有不同的长度。
例如,一个2阶张量可以表示为一个矩阵,其中有两个指标(行和列)。一个3阶张量可以表示为一个立方体或一个由多个矩阵组成的集合,其中有三个指标(行、列和高度)。
张量具有一些重要的性质和运算规则,包括张量的加法、乘法、收缩等。根据运算规则和性质,可以定义张量的转置、逆、对称性等概念。
总结来说,张量是用于表示多维数组的扩展概念。它在线性代数、多线性代数和各种科学领域中都具有重要的应用,是描述和处理多维数据的有力工具。
四、希尔伯特空间
希尔伯特空间(Hilbert Space)是数学中的一个重要概念,它是一个完备的内积空间。希尔伯特空间在量子力学和函数分析等领域中具有重要的应用。
一个希尔伯特空间H是一个向量空间,其中定义了一个内积运算,满足以下性质:
- 线性性:对于任意的向量x, y, z ∈ H和任意的标量a, b,有内积的线性性质:⟨ax + by, z⟩ = a⟨x, z⟩ + b⟨y, z⟩。
- 共轭对称性:对于任意的向量x, y ∈ H,有共轭对称性:⟨x, y⟩ = ⟨y, x⟩,其中表示复数的共轭。
- 正定性:对于任意的非零向量x ∈ H,有正定性:⟨x, x⟩ > 0,且当且仅当x = 0时等号成立。
在希尔伯特空间中,我们可以定义向量的模长(或范数),即向量x的模长为∥x∥ = √⟨x, x⟩。这个模长定义了希尔伯特空间的度量结构。
希尔伯特空间的一个重要特性是完备性。一个向量序列{xn}在希尔伯特空间H中是收敛的,当且仅当存在一个向量x ∈ H,使得序列{xn}收敛于x。这意味着希尔伯特空间中的任何柯西序列都收敛于一个向量。
希尔伯特空间在量子力学中起着重要的作用,量子态可以视为希尔伯特空间中的向量,量子力学中的算符可以表示为希尔伯特空间上的线性算符。希尔伯特空间为量子力学提供了一个数学框架,用于描述和分析量子系统的态和算符。
总结来说,希尔伯特空间是一个完备的内积空间,具有线性性、共轭对称性和正定性。它在量子力学和函数分析等领域中广泛应用,用于描述和分析向量、算符和量子系统的态。
五、张量积
张量积(Tensor Product)是线性代数中的一种运算,用于将两个向量空间的向量组合成一个更大的向量空间。
设V和W是两个向量空间,分别由基向量{v₁, v₂, …, vₙ}和{w₁, w₂, …, wₘ}生成。那么它们的张量积V ⊗ W定义为由所有可能的对积向量(vᵢ ⊗ wⱼ)组成的向量空间生成。
具体来说,张量积的定义如下:
- V ⊗ W = Span{(vᵢ ⊗ wⱼ) | 1 ≤ i ≤ n, 1 ≤ j ≤ m}
其中,⊗ 表示张量积运算,vᵢ ⊗ wⱼ表示向量vᵢ和wⱼ的张量积。张量积的结果是一个新的向量空间,其维度为V的维度乘以W的维度。
张量积有以下性质:
-
分配律:对于向量空间V, W, X,有(V ⊗ (W + X)) = (V ⊗ W) + (V ⊗ X)和((V + W) ⊗ X) = (V ⊗ X) + (W ⊗ X)。
-
结合律:对于向量空间V, W, X,有(V ⊗ (W ⊗ X)) = ((V ⊗ W) ⊗ X)。
-
基向量的张量积:如果V由基向量{v₁, v₂, …, vₙ}生成,W由基向量{w₁, w₂, …, wₘ}生成,那么它们的基向量的张量积为{(vᵢ ⊗ wⱼ) | 1 ≤ i ≤ n, 1 ≤ j ≤ m},生成了V ⊗ W。
张量积在多线性代数、量子力学和计算机科学等领域中有广泛应用。在量子力学中,张量积用于描述多粒子系统的态空间,以及计算复合系统的态和操作。在计算机科学中,张量积被用于构建神经网络模型和处理多维数据。
总结来说,张量积是将两个向量空间的向量组合成一个更大的向量空间的运算。它具有分配律和结合律等性质,用于描述多粒子系统、构建神经网络和处理多维数据。
六、泡利矩阵
泡利矩阵(Pauli Matrices)是一组重要的2×2复数矩阵,在量子力学和量子信息理论中经常使用。它们由物理学家维尔纳·泡利(Werner Pauli)在20世纪早期引入,以描述自旋系统的性质。
泡利矩阵一共有三个,分别记为σ₁、σ₂和σ₃。它们的具体定义如下:
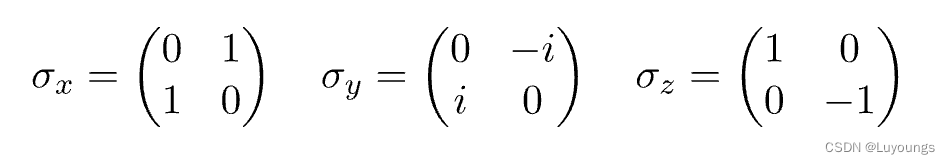
其中,i是虚数单位。这里的0和1代表2×2单位矩阵的元素。
这些矩阵具有以下性质:
- Hermite性:泡利矩阵是厄米矩阵,即它们与自身的共轭转置相等。
- 幺正矩阵。
- 幂等性:每个泡利矩阵的平方等于单位矩阵,即σ₁² = σ₂² = σ₃² = I,其中I是2×2单位矩阵。
- 对易性:任意两个不同的泡利矩阵之间是对易的,即[σᵢ, σⱼ] = 0,其中[i, j]表示i不等于j。
- 归一性:泡利矩阵的模长为1,即|σ₁| = |σ₂| = |σ₃| = 1。
泡利矩阵在量子力学中有广泛的应用。它们是描述自旋1/2粒子的自旋矩阵,用于计算自旋态的变换和测量。它们也是构成量子比特的基本门操作的泡利算符。在量子计算和量子信息理论中,泡利矩阵用于描述量子比特的操作和态的变换,以及构建量子门和量子算法。
总之,泡利矩阵是一组重要的2×2复数矩阵,用于描述自旋系统和量子比特的性质,在量子力学和量子信息理论中起着重要的作用。
七、克罗内克函数
在数学中,Kronecker delta(以 Leopold Kronecker 命名)是两个变量的函数,通常只是非负整数。 如果变量相等,则函数为1,否则为0:
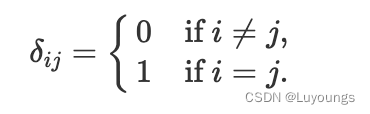
相关文章:
泡利矩阵(一)
〇、厄米矩阵 厄米矩阵(Hermitian Matrix),也称为自共轭矩阵(Self-adjoint Matrix),是线性代数中的一个重要概念。它是指一个复数域上的方阵,其转置矩阵与共轭矩阵相等。 具体来说,…...

通用支付系统设计
支付永远是一个公司的核心领域,因为这是一个有交易属性公司的命脉。那么,支付系统到底长什么样,又是怎么运行交互的呢?抛开带有支付牌照的金融公司的支付架构,下述链路和系统组成基本上符合绝大多数支付场景。其实整体可以看成是…...

metaRTC+ZLMediaKit实现webrtc的推拉流
概述 ZLMediaKit是一个基于C11的高性能运营级流媒体服务框架,是一个支持webrtc SFU的优秀的流媒体服务器系统。 metaRTC新版本支持whip/whep协议,支持whip/whep协议的ZLMediaKit推拉流。 信令通信 ZLMediaKit新版本支持whip和whep协议,支…...
【JavaSE】Java基础语法(八)
文章目录 🍓1. 类和对象🍹🍹1.1 类和对象的关系🍹🍹1.2 类的定义 🍓2. 对象内存图🍹🍹2.1 单个对象内存图🍹🍹2.2 多个对象内存图2.3 多个对象指向相同内存图…...
Java如何配置环境变量
Java如何配置环境变量 0. 前言1. 下载Java2. 配置环境变量2.1新建 Java_Home2.2 编辑Path情况1情况2 3. 验证安装 0. 前言 本节记录如何配置Java环境变量,用自己重装过的系统实操 操作系统:Windows10 专业版 Java版本:jdk1.7.0_07 1. 下载…...

android 12.0SystemUI 状态栏下拉快捷添加截图快捷开关
1.概述 在12.0的系统产品rom定制化开发中,对SystemUI的定制需求也是挺多的,在下拉状态栏中 添加截图快捷开关,也是常有的开发功能,下面就以添加 截图功能为例功能的实现 2.SystemUI 状态栏下拉快捷添加截图快捷开关的核心代码 frameworks/base/packages/SystemUI/res/va…...
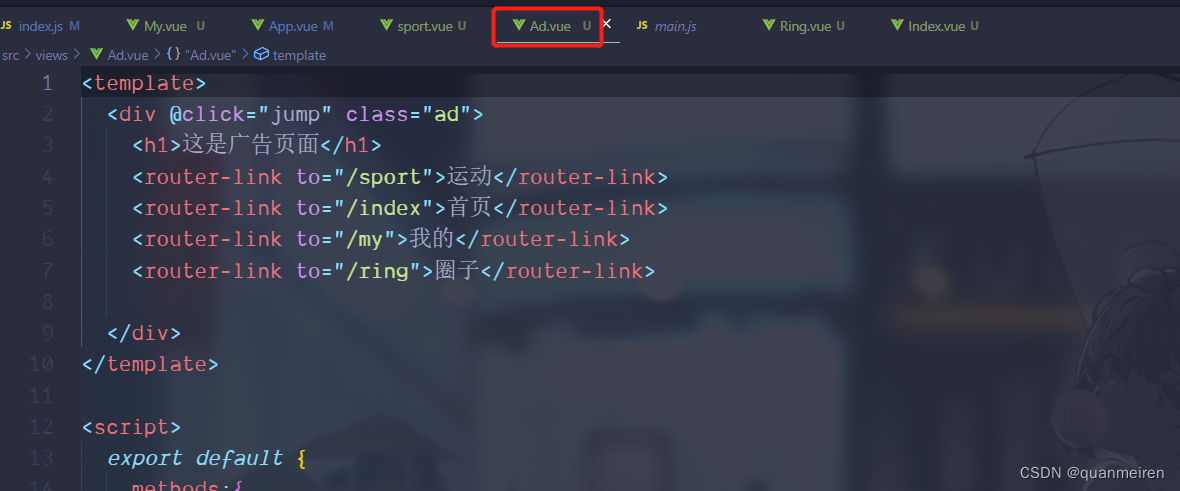
【无标题】 Vue 路由库Router 【重点】 - 安装 - 基本使用 - 路由配置 - 路由模式 - 路由传递参数 - 路由内置对象 - 路由守卫
0.0 课程介绍 Vue 路由库Router 【重点】 安装基本使用路由配置路由模式路由传递参数路由内置对象路由守卫 Vue的内置API 【掌握】 ref Vue.set Vue.nextTick Vue.filter Vue.component Vue.use Vue.directive 1.0 Vue的路由Router 【重点】 1.1 路由作用 进行页面…...
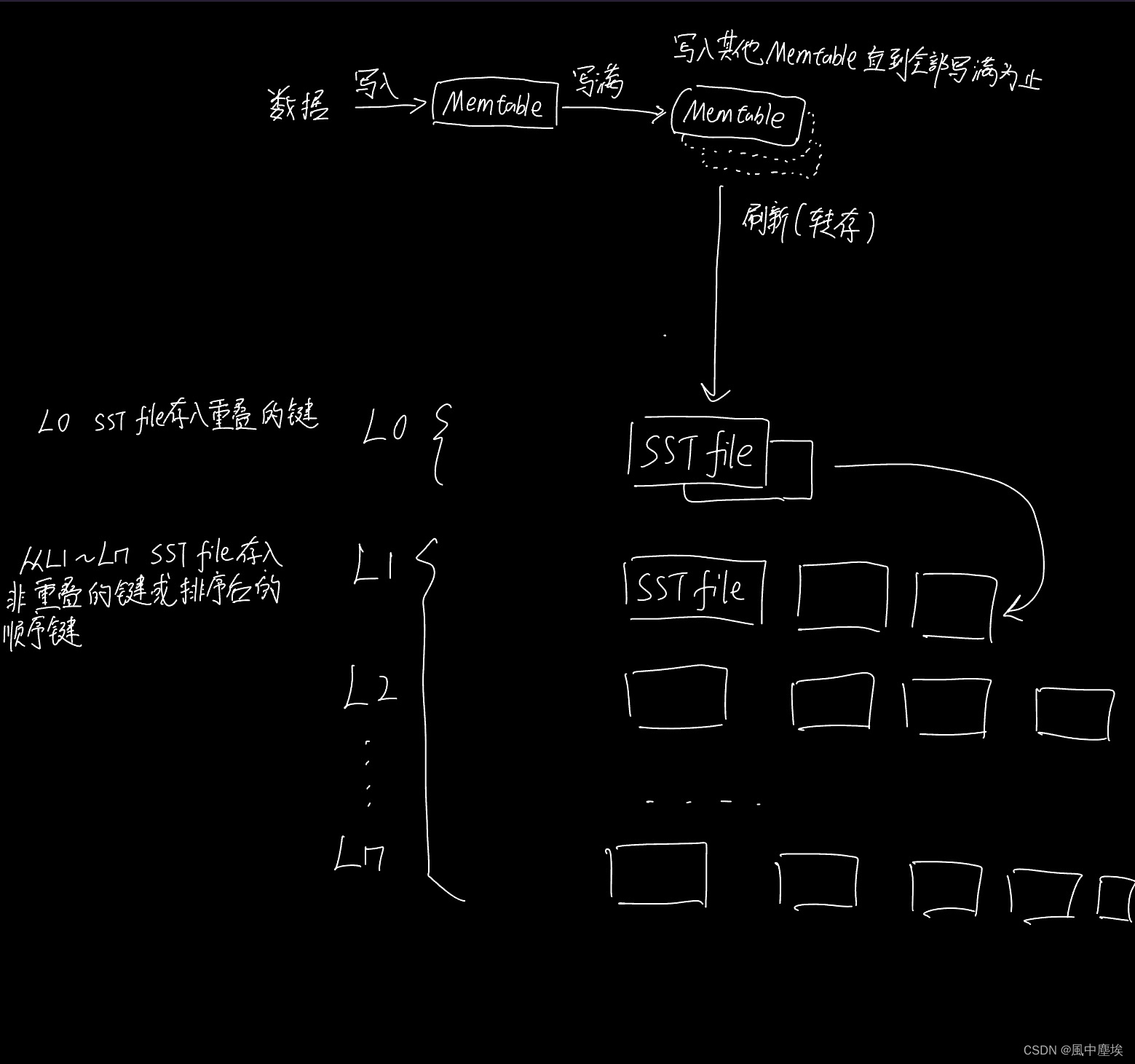
RocksDB笔记 -- 整体架构
RocksDB是由Facebook开发的存储引擎, 它最初的目标是用于快速存储, 特别是Flash存储. 一个基于C开发keys-values存储引擎库. 整体架构 RocksDB由这三个基本结构组成: memtable, sstfile 和 logfile. 其中: memtable是一个内存数据结构, 新的写入会插入到memtable中, 同时可选…...
设计模式之单例模式入门介绍
一、设计模式概念 设计模式是被广泛使用的软件开发中的一种解决方案,它提供了一套被验证过的、可重用的设计思想,帮助开发人员更加高效地开发出可维护、易扩展的软件系统。 设计模式可以分为三类:创建型模式、结构型模式和行为型模式。 1.1…...

RHCE 作业三
1.基于域名访问网站 [rootserver ~]# setenforce 0 [rootserver ~]# systemctl stop firewalld [rootserver ~]# systemctl disable firewalld [rootserver ~]# yum install httpd -y [rootserver ~]# systemctl start httpd [rootserver ~]# syst…...
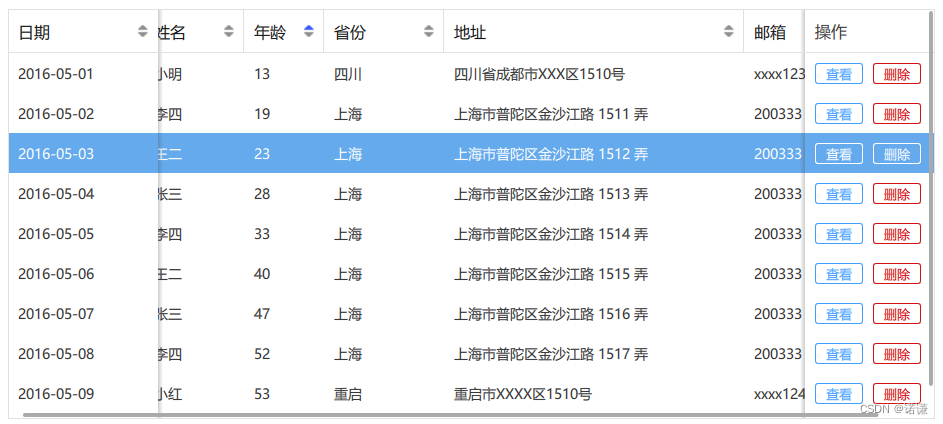
90.qt qml-Table表格组件(支持表头表尾固定/自定义颜色/自定义操作按钮/插入排序)
众所周知,qml table在目前版本还很废,qt5的table完全就没法用,在之前章节就写过: 88.qt qml-TableView学习(一)_诺谦的博客-CSDN博客 所以本章便参考VUE-Element的Table外观组件实现一个可排序可操作的Table组件. 1.组件介绍 GIF如下所示: 排序支持数字和字符串排序。 …...

android 12.0SystemUI屏蔽某个app的通知
1.概述 在12.0的产品开发中,对于系统的通知部分,要求根据app包名来过滤掉一部分通知,就是在接收到系统通知时,根据包名判断是否需要接收通知的功能,首选要分析通知流程,然后实现功能 2.SystemUI屏蔽某个app的通知相关代码 frameworks\base\packages\SystemUI\src\com\…...
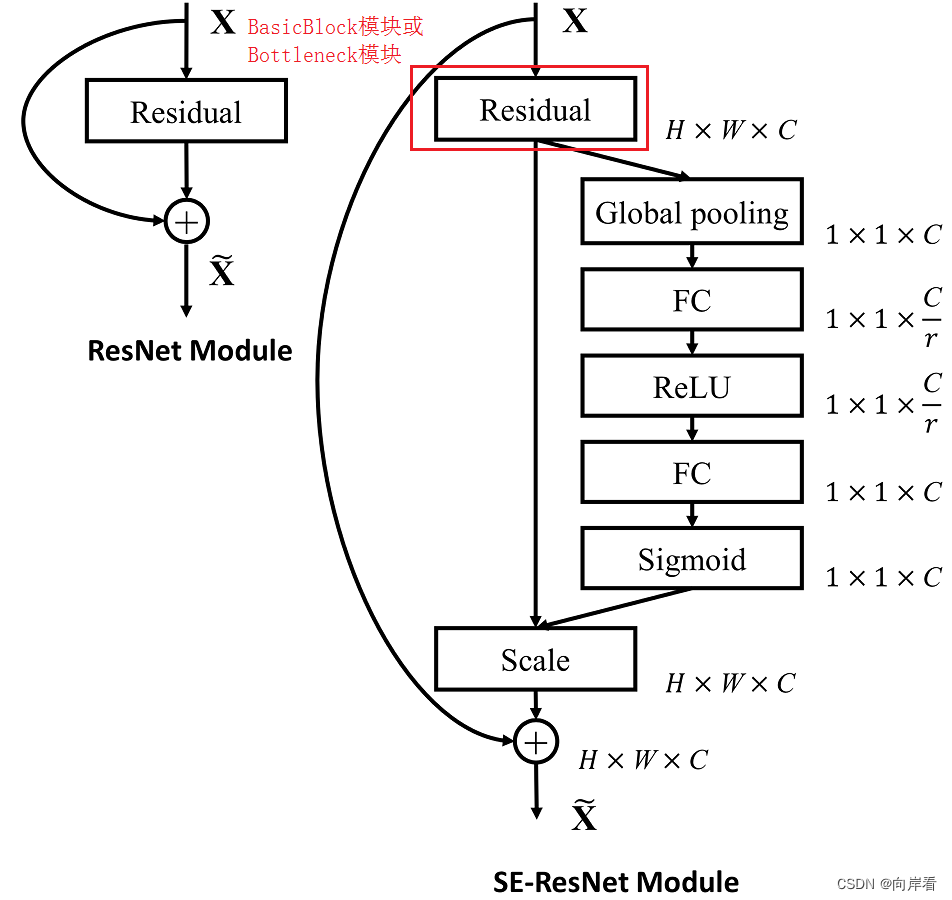
注意力机制(一)SE模块(Squeeze-and-Excitation Networks)论文总结和代码实现
Squeeze-and-Excitation Networks(压缩和激励网络) 论文地址:Squeeze-and-Excitation Networks 论文中文版:Squeeze-and-Excitation Networks_中文版 代码地址:GitHub - hujie-frank/SENet: Squeeze-and-Excitation Ne…...
L2-001 紧急救援(dijkstra算法练习)
作为一个城市的应急救援队伍的负责人,你有一张特殊的全国地图。在地图上显示有多个分散的城市和一些连接城市的快速道路。每个城市的救援队数量和每一条连接两个城市的快速道路长度都标在地图上。当其他城市有紧急求助电话给你的时候,你的任务是带领你的…...
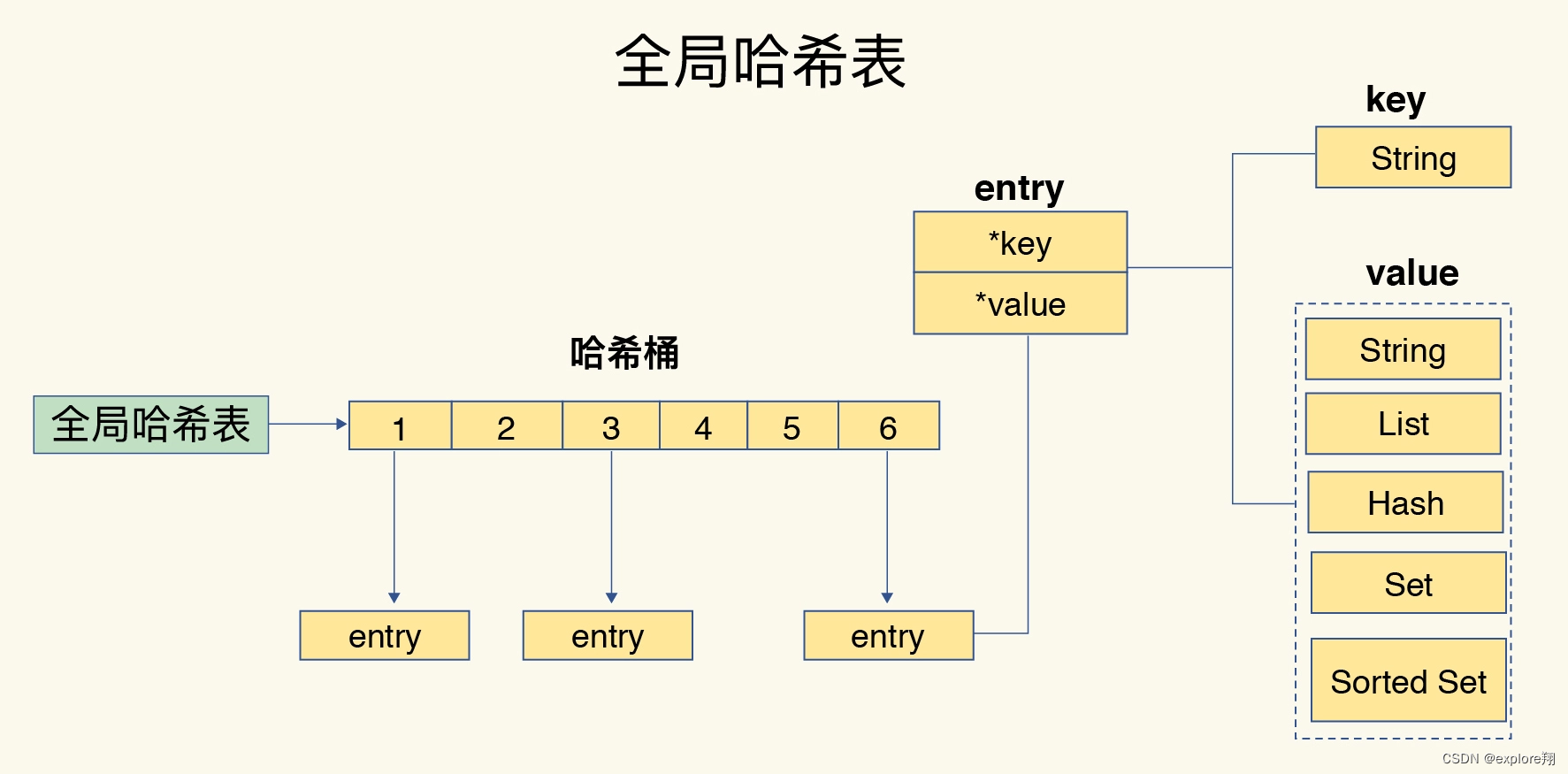
redis问题汇总
redis的优点 读写性能优异。十万/s的量级; 支持数据持久化。AOF,RDB 支持丰富的数据类型; 支持集群,可以实现主从复制,哨兵机制迁移,扩容等 缺点: 因为是基于内存的,所以虽然redis本身有key过期…...

调用华为API实现情感分析
作者介绍 王新华,男,西安工程大学电子信息学院,2022级研究生 研究方向:人工智能与模式识别 电子邮件:996514274qq.com 魏小双,女,西安工程大学电子信息学院,2022级研究生 研究方向…...

C# 静态构造函数
静态构造函数用于初始化任何静态数据,或执行仅需要执行一次的特定操作。在创建第一个实例或引用任何静态成员之前,将自动调用它。 静态构造函数是在构造函数方法前面添加了static关键字之后形成的,并且没有修饰符(public,private),没有参数。…...

【C++】哈希表特性总结及unordered_map和unordered_set的模拟实现
✍作者:阿润菜菜 📖专栏:C 文章目录 前言一、哈希表的特性 - 哈希函数和哈希冲突1 哈希函数2. 哈希冲突 二、闭散列的实现 -- 开放地址法1. 定义数据结构2.insert()3.Find()4. Erase()5.仿函数处理key值不能取模无法映射 --- BKDRHash 三、开…...
)
Qt在Linux内核中的应用及解析(qtlinux内核)
Qt是跨平台开发的一种工具,尤其适合在Linux内核中的应用开发中使用。Qt能够让开发者在Linux桌面上开发出强大的图形化应用程序,为Linux系统用户提供更加人性化、实用、智能化的服务。本文将从Qt在Linux内核中的应用场景、应用程序开发中的具体使用、以及…...
Xpdf 阅读器源码编译后查看文件中文乱码问题解决
经查阅,是由于缺少中文字体包: 第一步:下载所需要的字体包 下载https://dl.xpdfreader.com/xpdf-t1fonts.tar.gz 包含下载中文字体包(非嵌入字体) http://ftp.gnu.org/gnu/non-gnu/chinese-fonts-truetype/gkai00mp…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
