L2-001 紧急救援(dijkstra算法练习)
作为一个城市的应急救援队伍的负责人,你有一张特殊的全国地图。在地图上显示有多个分散的城市和一些连接城市的快速道路。每个城市的救援队数量和每一条连接两个城市的快速道路长度都标在地图上。当其他城市有紧急求助电话给你的时候,你的任务是带领你的救援队尽快赶往事发地,同时,一路上召集尽可能多的救援队。
输入格式:
输入第一行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0 ~ (N−1);M是快速道路的条数;S是出发地的城市编号;D是目的地的城市编号。
第二行给出N个正整数,其中第i个数是第i个城市的救援队的数目,数字间以空格分隔。随后的M行中,每行给出一条快速道路的信息,分别是:城市1、城市2、快速道路的长度,中间用空格分开,数字均为整数且不超过500。输入保证救援可行且最优解唯一。
输出格式:
第一行输出最短路径的条数和能够召集的最多的救援队数量。第二行输出从S到D的路径中经过的城市编号。数字间以空格分隔,输出结尾不能有多余空格。
输入样例:
4 5 0 3
20 30 40 10
0 1 1
1 3 2
0 3 3
0 2 2
2 3 2
输出样例:
2 60
0 1 3首先:最简单的就是无脑DFS搜索全部情况返回最优解
#include<bits/stdc++.h>
using namespace std;
const int maxn = 510;
int N, M, S, D, A, B, C, road = 0, love, mind = 1 << 20;//路径 救援数
vector<int>sove(maxn);
int MAP[maxn][maxn];
deque<int>ans;
deque<int>s;
bool vis[maxn][maxn];
void DFS(int str, int end, int d, int sum)//起始 结尾 路径 救援数
{if (str == end && mind >= d){ //达到目的地 if(mind > d){road = 0;ans = s;mind = d;love = sum;}else if(d == mind && love < sum){love = sum;ans = s;}road++;return;}else if(str == end)return;for (int i = 0; i < N; i++){if (MAP[str][i] && !vis[str][i]){vis[str][i] = true;s.push_back(i);DFS(i, end, d + MAP[str][i], sum + sove[i]);vis[str][i] = false;s.pop_back();}}
}int main()
{cin >> N >> M >> S >> D;for (int i = 0; i < N; i++){cin >> sove[i];}for (int i = 0; i < M; i++){cin >> A >> B >> C;MAP[A][B] = MAP[B][A] = C;}DFS(S, D, 0, sove[S]);cout << road << " " << love << endl << S;while (!ans.empty()){cout << " " << ans.front();ans.pop_front();}return 0;
}但是缺陷也是比较明显的,如果图中各节点的联通网十分密集的话,那我们递归的深度就很容易导致系统栈被压爆,从而得不出答案
那么就得涉及到最短路径算法了,常见的Dijkstra或者Floyd
当然也有Bellman 和 SPFA但是对于这题效果不如dijkstra
简单的科普Dijkstra和Floyd算法
最短路径(Dijkstra算法和Floyd算法)_法苏ovo的博客-CSDN博客
基于Floyd大多是处理任意俩点最短路径(并且效率较低)而我们这题侧重于单源路径,就采用Dijikstra进行解题
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
const int maxn = 510;
int N, M, S, D, A, B, len;
vector<int>p(maxn), pre(maxn, -1), num(maxn), per(maxn), dis(maxn, INT_MAX);
// 各点的救援队数量 前置结点 从起点到该点的最短路数量 从起点到该点最短路的救援队数量 从起点到该点的最短距离
bool vis[maxn];
struct edge
{int to, len;edge(int a, int b) : to(a), len(b) {};
};
vector<edge>e[maxn];
struct q_node
{int id, dis;q_node(int a, int b) :id(a), dis(b) {};bool operator< (const q_node& s)const{return dis > s.dis;}
};
void printf_path(int x)
{if (pre[x] == -1) return;printf_path(pre[x]);printf(" %d", x);
}
void dijkstra()
{dis[S] = 0, num[S] = 1, per[S] = p[S];priority_queue<q_node>Q;Q.emplace(S, dis[S]);while (!Q.empty()){auto x = Q.top();Q.pop();if (vis[x.id])continue;vis[x.id] = true;for (int i = 0; i < e[x.id].size(); i++){auto y = e[x.id][i];//枚举邻居if (dis[y.to] == dis[x.id] + y.len)num[y.to] += num[x.id];if (dis[y.to] > dis[x.id] + y.len)num[y.to] = num[x.id];if ((dis[y.to] == dis[x.id] + y.len && per[y.to] < per[x.id] + p[y.to]) || dis[y.to] > dis[x.id] + y.len){per[y.to] = per[x.id] + p[y.to];pre[y.to] = x.id;dis[y.to] = dis[x.id] + y.len;Q.emplace(y.to, dis[y.to]);}}}
}
int main()
{cin >> N >> M >> S >> D;for (int i = 0; i < N; i++)cin >> p[i];while (M--){cin >> A >> B >> len;e[A].emplace_back(B, len);e[B].emplace_back(A, len);}dijkstra();cout << num[D] << " " << per[D] << endl << S;printf_path(D);return 0;
}Dijkstra算法练习
公交线路 (nowcoder.com)
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1010;
int n,m,s,t,A,B,len;
struct edge
{int form,to,len;edge(int a,int b,int c) : form(a),to(b),len(c){};
};
vector<edge>e[maxn];
vector<int>dis(maxn,0x3f3f3f3f),pre(maxn);
bool vis[maxn];
struct q_node
{int id,dis;q_node(int a,int b):id(a),dis(b){};bool operator < (const q_node& s)const{return dis > s.dis;}
};
void dijkstra()
{dis[s] = 0;priority_queue<q_node>Q;Q.emplace(s,dis[s]);while(!Q.empty()){auto x = Q.top();Q.pop();if(vis[x.id])continue;vis[x.id] = true;for(int i = 0;i < e[x.id].size();i++){auto y = e[x.id][i];if(vis[y.to])continue;if(dis[y.to] > x.dis + y.len){dis[y.to] = x.dis + y.len;pre[y.to] = x.id;Q.emplace(y.to,dis[y.to]);}}}
}
int main()
{cin.tie(0)->sync_with_stdio(false);cin >> n >> m >> s >> t;while(m--){cin >> A >> B >> len;e[A].emplace_back(A,B,len);e[B].emplace_back(B,A,len);}dijkstra();dis[t] == 0x3f3f3f3f ? cout << -1 << endl : cout << dis[t] << endl;return 0;
}相关文章:

L2-001 紧急救援(dijkstra算法练习)
作为一个城市的应急救援队伍的负责人,你有一张特殊的全国地图。在地图上显示有多个分散的城市和一些连接城市的快速道路。每个城市的救援队数量和每一条连接两个城市的快速道路长度都标在地图上。当其他城市有紧急求助电话给你的时候,你的任务是带领你的…...
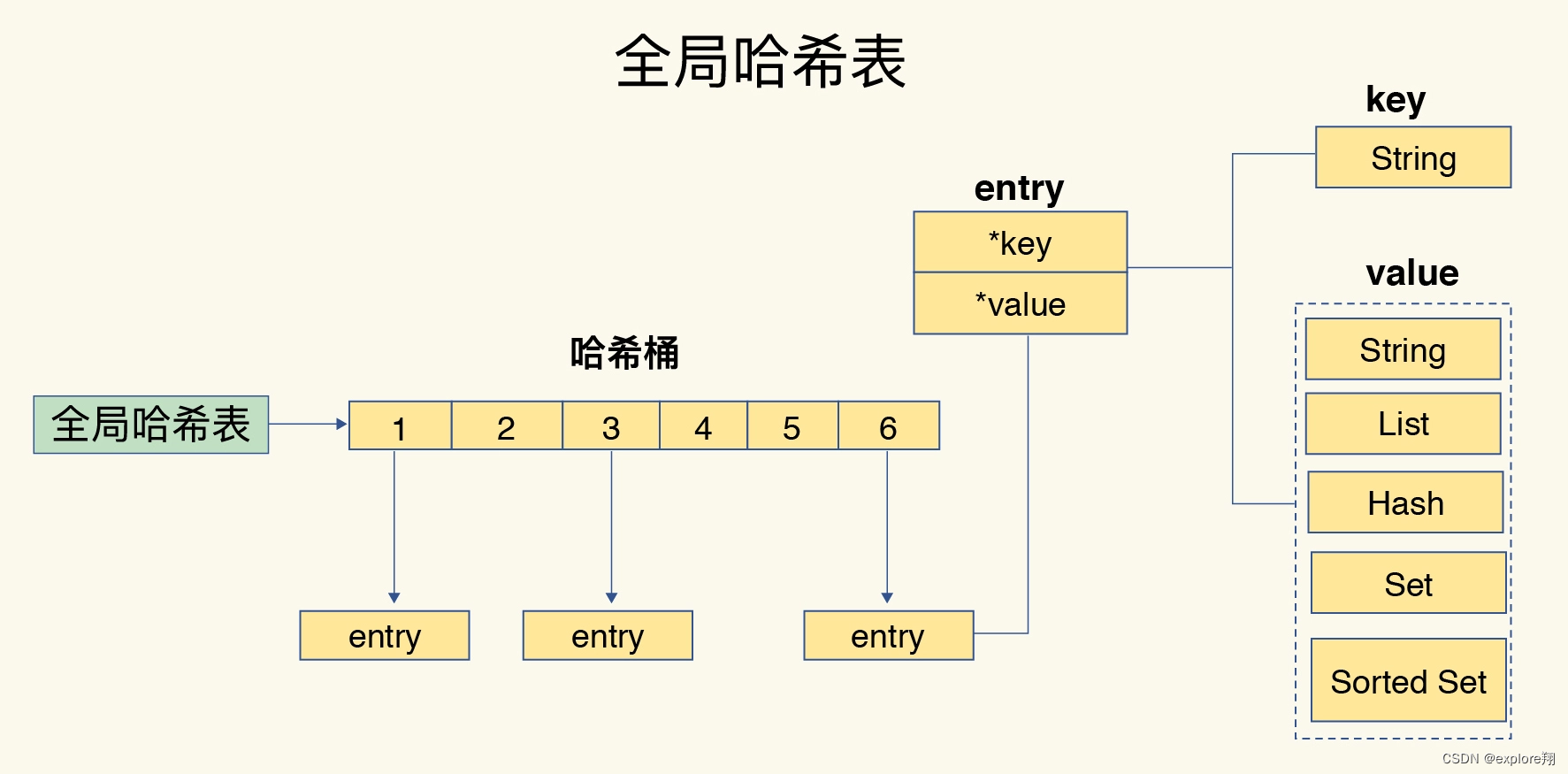
redis问题汇总
redis的优点 读写性能优异。十万/s的量级; 支持数据持久化。AOF,RDB 支持丰富的数据类型; 支持集群,可以实现主从复制,哨兵机制迁移,扩容等 缺点: 因为是基于内存的,所以虽然redis本身有key过期…...

调用华为API实现情感分析
作者介绍 王新华,男,西安工程大学电子信息学院,2022级研究生 研究方向:人工智能与模式识别 电子邮件:996514274qq.com 魏小双,女,西安工程大学电子信息学院,2022级研究生 研究方向…...

C# 静态构造函数
静态构造函数用于初始化任何静态数据,或执行仅需要执行一次的特定操作。在创建第一个实例或引用任何静态成员之前,将自动调用它。 静态构造函数是在构造函数方法前面添加了static关键字之后形成的,并且没有修饰符(public,private),没有参数。…...

【C++】哈希表特性总结及unordered_map和unordered_set的模拟实现
✍作者:阿润菜菜 📖专栏:C 文章目录 前言一、哈希表的特性 - 哈希函数和哈希冲突1 哈希函数2. 哈希冲突 二、闭散列的实现 -- 开放地址法1. 定义数据结构2.insert()3.Find()4. Erase()5.仿函数处理key值不能取模无法映射 --- BKDRHash 三、开…...
)
Qt在Linux内核中的应用及解析(qtlinux内核)
Qt是跨平台开发的一种工具,尤其适合在Linux内核中的应用开发中使用。Qt能够让开发者在Linux桌面上开发出强大的图形化应用程序,为Linux系统用户提供更加人性化、实用、智能化的服务。本文将从Qt在Linux内核中的应用场景、应用程序开发中的具体使用、以及…...
Xpdf 阅读器源码编译后查看文件中文乱码问题解决
经查阅,是由于缺少中文字体包: 第一步:下载所需要的字体包 下载https://dl.xpdfreader.com/xpdf-t1fonts.tar.gz 包含下载中文字体包(非嵌入字体) http://ftp.gnu.org/gnu/non-gnu/chinese-fonts-truetype/gkai00mp…...
)
Java - AQS-CountDownLatch实现类(二)
前言 在Java中,AbstractQueuedSynchronizer(简称AQS)是一个用于实现同步器的抽象类,它为实现各种类型的同步器(如锁、信号量等)提供了基本的框架。AQS通过一个双向队列(等待队列)和…...

rsut基础
这篇文章是实战性质的,也就是说原理部分较少,属于经验总结,rust对于模块的例子太少了。rust特性比较多(悲),本文的内容可能只是一部分,实现方式也不一定是这一种。 关于 rust 模块的相关内容&a…...

高压放大器和示波器的关系是什么
高压放大器和示波器是电子工程领域中常见的两种设备,它们在实际的电路设计、测试和分析中都扮演着重要的角色。下面安泰电子将从定义、功能、应用场景等方面为您介绍高压放大器和示波器的关系。 图:ATA-7000系列高压放大器 一、高压放大器的定义及功能 高…...
5个超实用视频素材网站,免费下载~
推荐几个高清无水印的视频素材网站,重点是可以免费下载使用,建议收藏! 菜鸟图库 https://www.sucai999.com/video.html?vNTYxMjky 可以称之为最大素材库,在这里你可以找到设计、办公、图片、视频、音频等各种素材。视频素材就有…...
(BoW、N-gram、tf-idf))
【NLP模型】文本建模(1)(BoW、N-gram、tf-idf)
目录 一、说明 二、BoW模型产生发展 2.1 产生和历史 2.2 原理介绍 三、具体实现...

Java——网络编程套接字
目录 一、网络编程基础 1.1 为什么需要网络编程?——丰富的网络资源 二、什么是网络编程? 三、网络编程中的基本概念 3.2 请求和响应 3.3 客户端和服务端 常见的客户端服务端模型 四、Socket套接字 五、通信模型 5.1 Java数据报套接字通信模型 5.2 Java流…...
160套小程序源码
源码列表如下: AppleMusic (知乎日报) 微信小程序 d artand 今日更新求职招聘类 医药网 口碑外卖点餐 城市天气 外卖小程序 定位天气 家居在线 微信小程序-大好商城,wechat-weapp 微信小程序的掘金信息流 微信跳一跳小游戏源码 微票源码-demo 急救应急处…...

有效项目进度管理的 10 条规则
项目进度管理是项目中比较关键的方面之一,因为它将决定事情的进展方式、进展速度以及是否会取得进展。换句话说,它可以让你较好地控制项目,帮助你预测不可预测的情况,并使所有相关团队能够高效地协同工作。 以下是有效项目进度管…...
javaWebssh服装租赁店信息管理系统台myeclipse开发mysql数据库MVC模式java编程计算机网页设计
一、源码特点 java ssh服装租赁店信息管理系统是一套完善的web设计系统(系统采用ssh框架进行设计开发),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要 采用B/S模式开发。开发环境为TO…...
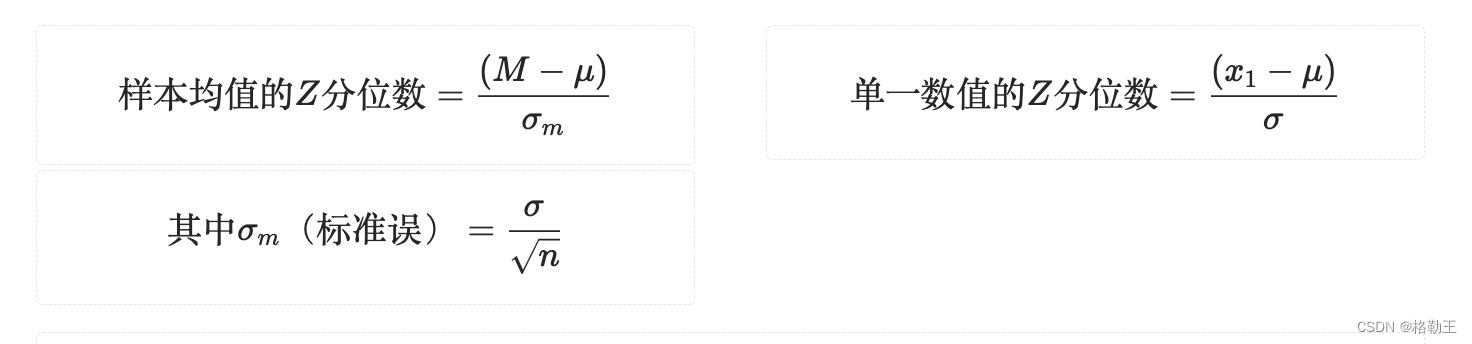
概率论:样本与总体分布,Z分数与概率
参考书目:《行为科学统计精要》(第八版)——弗雷德里克J格雷维特 数据及其样本的分布 描述一组数据分布 描述一组样本数据的分布 描述样本数据的均值和整体数据一样,但是样本标准差的公式除以了n-1,这里引入自由度的…...
【JavaSE】Java基础语法(十二):ArrayList
文章目录 1. ArrayList的构造方法和添加方法2. ArrayList类常用方法3. ArrayList存储学生对象并遍历 集合和数组的区别 : 共同点:都是存储数据的容器不同点:数组的容量是固定的,集合的容量是可变的 1. ArrayList的构造方法和添加方法 ArrayL…...

c++—封装:运算符重载、友元
1. 友元 (1)友元函数 ①是一种允许非类成员函数访问类的私有成员的一种机制;可以把一个函数指定为类的友元,也可以把整个类指定为另一个类的友元; ②友元函数在类作用域外定义,但需要在类体中进行声明&…...
【K8s】安全认证与DashBoard
文章目录 一、概述1、客户端2、认证、鉴权与准入控制 二、认证管理1、认证方式2、HTTPS证书认证 三、授权管理1、授权与RBAC2、Role 与 ClusterRole3、RoleBinding 与 ClusterRoleBinding4、案例:创建一个只能管理dev空间下Pods资源的账号 四、准入控制五、DashBoar…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...
