C语言数据结构——树、堆(堆排序)、TOPK问题
🐶博主主页:@ᰔᩚ. 一怀明月ꦿ
❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C++,数据结构
🔥座右铭:“不要等到什么都没有了,才下定决心去做”
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀
目录
树
树的概念
树的表示
二叉树
二叉树概念:
特殊的二叉树
二叉树的性质
二叉树的存储结构
2. 链式存储
堆
二叉树的顺序结构
堆的概念及结构
堆排序
堆排序的实现
建堆
堆排序
TOPK
树
树的概念
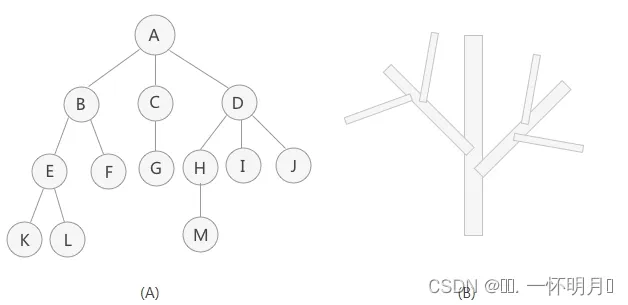
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
图1
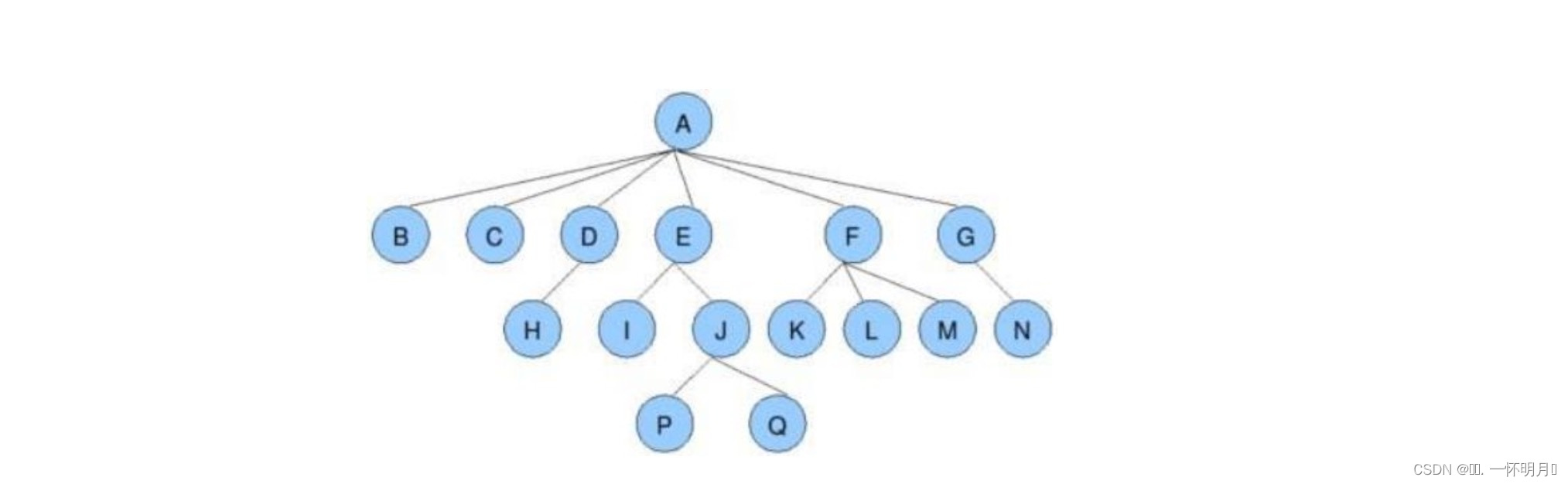
图2
节点的度:一个节点含有的子树的个数称为该节点的度;如图2:A的度为6
叶节点(终端节点):度为0的节点称为叶节点;如图2:B、C、H、I...等为叶节点
父节点(双亲节点):若一个节点含有子节点,则这个节点称为其子节点的父节点;如图2:A是B的父节点
子节点(孩子节点):一个节点含有的子树的根节点称为该节点的子节点;如图2:B是A的子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点;如图2:B、C是兄弟节点
树的度:一颗树中,最大的节点的度称为树的度;如图2:树的度为6
节点的层次:从根开始定义起,根为第一层,根的子节点为第二层,依次类推
树的高度(树的深度):树中节点的最大层次;如图2:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如图2:H、I互为堂兄弟节点
节点祖先:从根到该节点所经分支上的所有节点;如图2;A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙;如图2:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林
树的表示
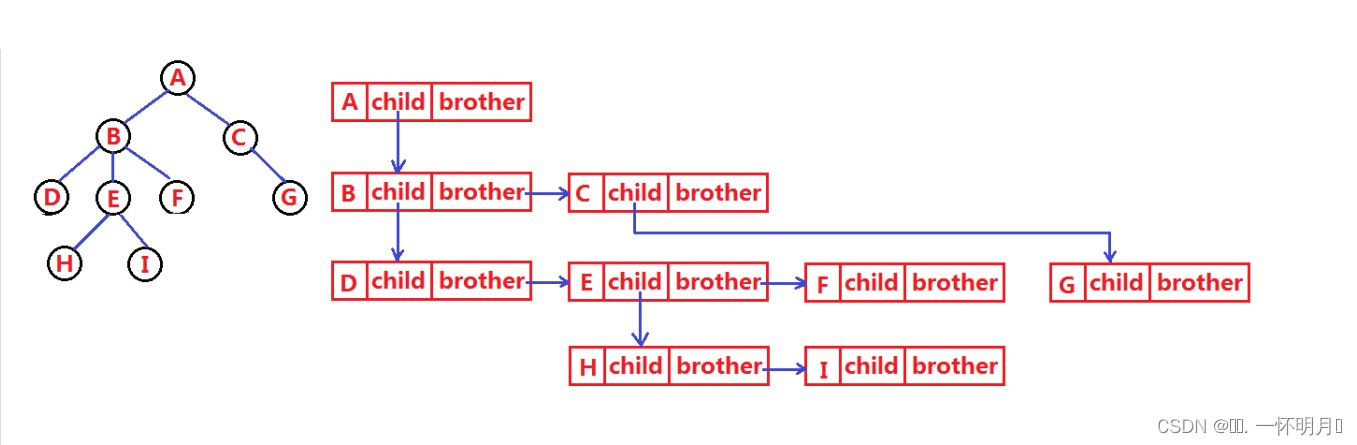
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法,即左孩子右兄弟表示法。
typedef int DataType; struct Node { struct Node* _firstChild1; // 第一个孩子结点 struct Node* _pNextBrother; // 指向其下一个兄弟结点 DataType _data; // 结点中的数据域 };
图3
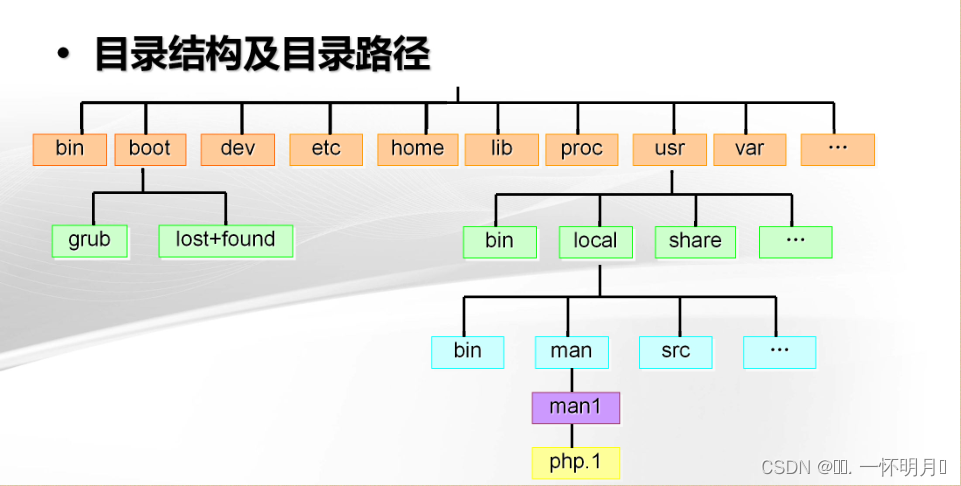
树在实际中的运用:表示文件系统的目录树结构
图4
二叉树
二叉树概念:
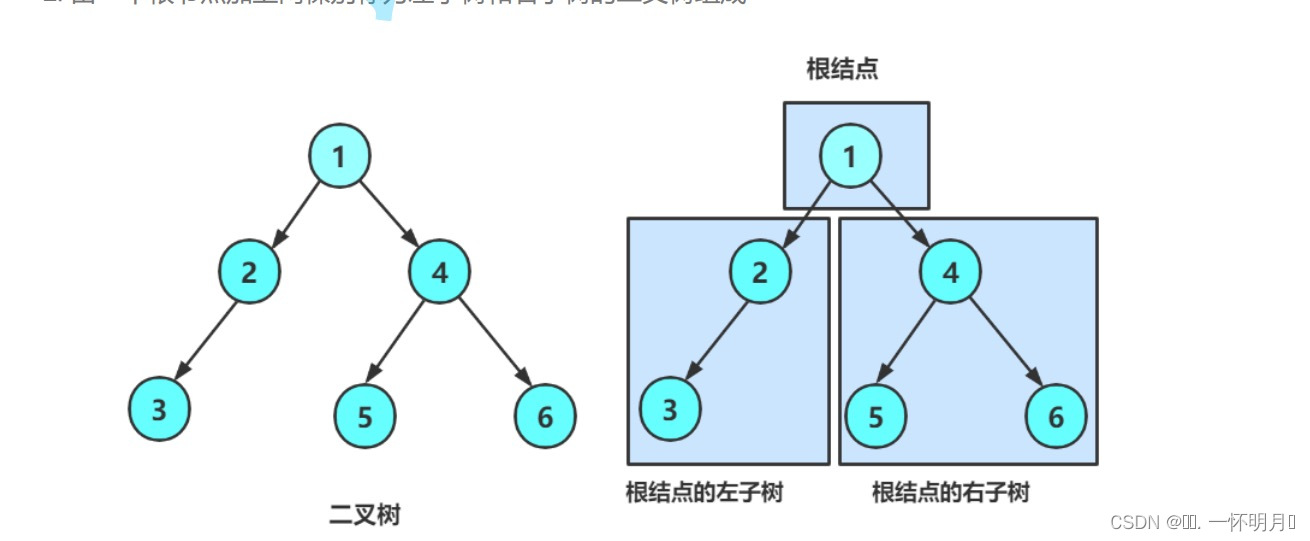
二叉树(Binary Tree)是n(n>=0)个结点的有限集合,该集合或者空集(称为空二叉树),或者由一个根节点和两颗互不相交的,分别称为根节点的左子树和右子树的二叉树组成。
图5
(1)二叉树的最大度为2;
(2)每个结点最多有两棵子树;
(3)左子树和右子树是有顺序的;
(4)即使树中某结点只有一颗子树,也要区分左右;
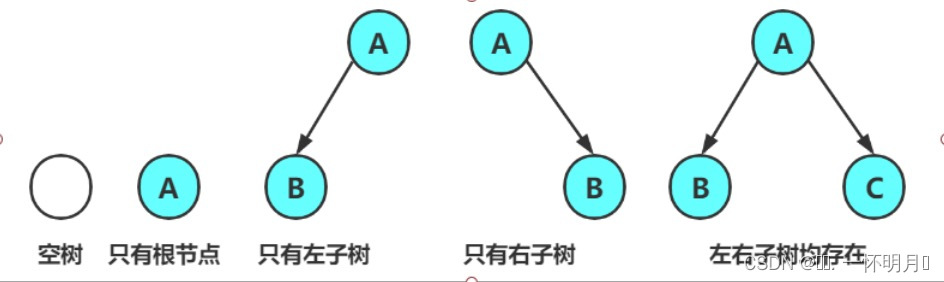
注意:对于任意的二叉树都是由以下几种情况复合而成的:
图6
特殊的二叉树
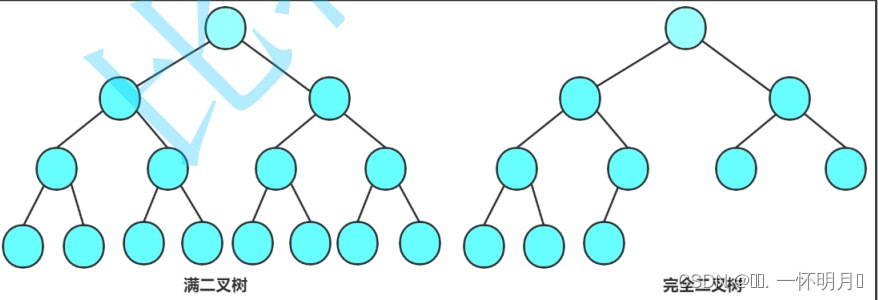
1.满二叉树:一个二叉树,如果每一层的节点数都达到了最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为k,且节点总数是2^k-1,则它是满二叉树。
2.完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为k的,有n个节点的二叉树,当且仅当每一个节点都与深度为k的满二叉树中编号从1至n的节点————对应时称之完全二叉树。要注意满二叉树是一种特殊的完全二叉树。
图7
二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1.
3. 对任何一棵二叉树, 如果度为0其叶结点个数为n0, 度为2的分支结点个数为 n2,则有n0=n2+1
4. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log2^(n+1) (是log以2为底,n+1为对数)
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
(1. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
(2. 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
(3. 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
1.顺序存储
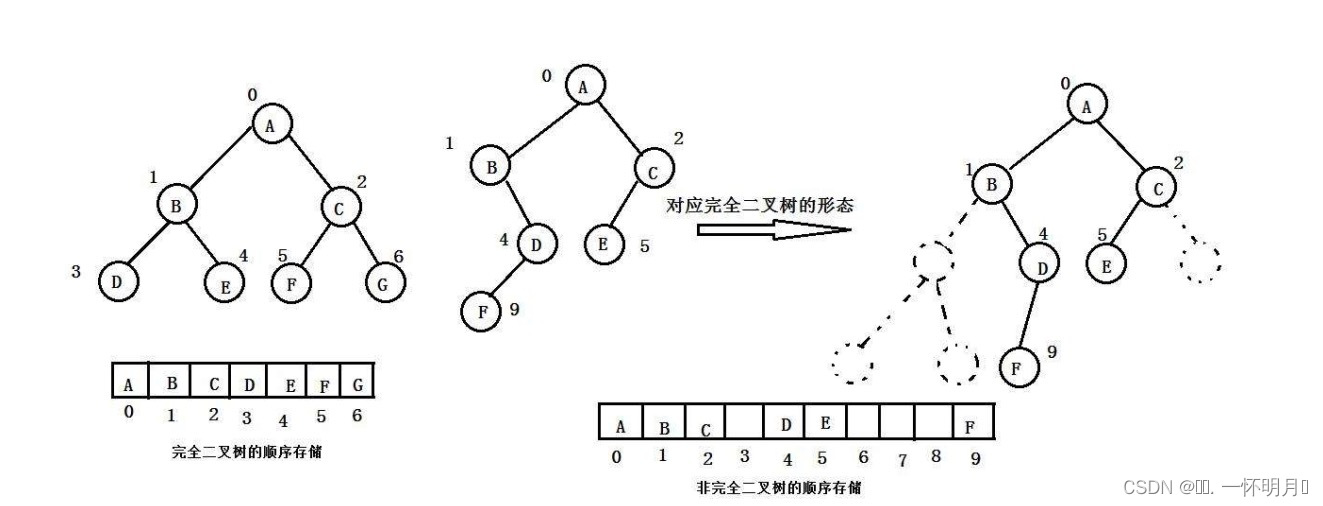
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树
图8
2. 链式存储
...
堆
二叉树的顺序结构
普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段
堆的概念及结构
如果有一个关键码的集合K = {k0,k1,k2,...,k[n-1] },把它的所有元素按完全二叉树的顺序存储方式存储
在一个一维数组中,并满足: Ki<=K[2*i+1] 且Ki<=K[2*i+2](Ki>=K[2*i+1] 且Ki>=K[2*i+2]),i=0,1,2...n
则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树
图9
堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,他的时间复杂度是O(N*logN)相较于冒泡排序(O(N*N))他的时间效率非常高。
堆排序的实现
1.将无序序列构建成一个堆,根据升序(降序)需求选择大根堆(小根堆)
2.将堆顶元素与末尾元素交换,将最大元素(最小元素)“沉”到数组末端
3.重新调整结构使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序
建堆
建堆有着两种建堆的方法,向上调整建堆和向下调整建堆,不管是建大根堆还是小根堆这两种方法都可以。
向上调整:
这里是准备建小根堆,Swap是交换函数(交换两个变量的值),判断最后一个孩子节点child的值是否比其父节点parent的值小,如果child的值比parent的值小,就交换父子节点的值,然后孩子节点child的位置移到父节点parent的位置,父节点parent移到父节点的父节点,然后再次判断孩子节点child的值与父节点parent的值的大小,直到child移到了根节点,如果child的值比parent的值如果大,就不用交换并且说明本次调整完成。
void AdjustUP(int* a,int n) {int child=n-1;int parent=(child-1)/2;while(child>0){if(a[child]<a[parent]){Swap(&a[child], &a[parent]);child=parent;parent=(child-1)/2;}else{break;}} }向下调整:
这里是准备建小根堆,判断父节点parent的值是否比其孩子节点child(一般父节点都有两个孩子节点,这里的孩子节点是两个中较小的那个)的值小,如果child的值比parent的值小,就交换父子节点的值,然后父节点parent的位置移到孩子节点child的位置,孩子节点child移到孩子节点的孩子节点的位置,然后再次判断孩子节点child的值与父节点parent的值的大小,直到child的值大于元素个数,如果child的值比parent的值如果大,就不用交换并且说明本次调整完成。
void AdjustDown(int* a,int n,int parent) {int child=parent*2+1;while(child<n){if(child+1<n&&a[child]>a[child+1]){child++;}if(a[child]<a[parent]){Swap(&a[child], &a[parent]);parent=child;child=parent*2+1;}else{break;}} }向上调整建堆:
向上建堆是从第二层开始直到第h层,所以其时间复杂度为O(N*logN)
for(int i=1;i<n;i++){AdjustUP(a, i);}向下调整建堆:
向下建堆是从第h-1层直到第一层,所以其时间复杂度为O(N)
for(int i=(n-1-1)/2;i>=0;i--){AdjustDown(a, n,i);}堆排序
由于有两种建堆方式,向上调整建堆和向下调整建堆,所以就有两种堆排序方式。
HeapSort_UP(向上建堆排序):
//时间复杂度为O(N*logN) void HeapSort_UP(int* a,int n) {//向上建堆是从第二层开始直到第h层,所以其时间复杂度为O(N*logN)for(int i=1;i<n;i++){AdjustUP(a, i);}int end=n-1;//建堆完成后,需要进行向下调整其时间复杂度为O(N*logN)while(end>0){Swap(&a[0], &a[end]);AdjustDown(a, end,0);end--;} }HeapSort_Down(向下建堆排序):
//时间复杂度为N*logN void HeapSort_Down(int* a,int n) {//向下建堆是从第h-1层直到第一层,所以其时间复杂度为O(N)for(int i=(n-1-1)/2;i>=0;i--){AdjustDown(a, n,i);}int end=n-1;//建堆完成后,需要进行向下调整其时间复杂度为O(N*logN)while(end>0){Swap(&a[0], &a[end]);AdjustDown(a, end,0);end--;} }总结:向上建堆从第二层开始直到第h层,向下建堆是从第h-1层直到第一层,虽然它们经历的层数相同,但是向上建堆中第一层不用调整,向下建堆中第h层不用调整(h为最后一层),第一层的元素只有一个,第h层元素有2^(h-1)个。所以他们的时间复杂度不同,向上建堆为O(N*logN),向下建堆为O(N),尽量使用向下建堆的方式来实现堆排序。
TOPK
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素,将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。例如:我们这里实现在1000000个数中找出5个最大的数,为了方便实现我们使用rand()生成1000000个数。为了贴近实战项目,我们会将这1000000个数据写到文件中,然后文件中读取。
#include<stdio.h> #include<stdlib.h> #include<time.h> void Swap(int* e1,int* e2) {int temp=*e1;*e1=*e2;*e2=temp; } void AdjustDown(int* a,int n,int parent) {int child=parent*2+1;while(child<n){if(child+1<n&&a[child]>a[child+1]){child++;}if(a[child]<a[parent]){Swap(&a[child], &a[parent]);parent=child;child=parent*2+1;}else{break;}} } void CreatData(void) {//system("pwd\n");int n=1000;srand((unsigned int)time(NULL));const char* file="data.txt";FILE* fout=fopen(file, "w");for(int i=0;i<n;i++){int x=rand()%1000000;fprintf(fout, "%d\n",x);}fclose(fout); } void PrintTopk(int k) {const char* file="data.txt";FILE* fin=fopen(file, "r");int* kminheap=(int*)malloc(sizeof(int)*k);for(int i=0;i<k;i++){fscanf(fin,"%d",&kminheap[i]);}//建小堆,for(int i=(k-1-1)/2;i>=0;i--){AdjustDown(kminheap, k, i);}int val=0;while(!feof(fin)){fscanf(fin, "%d",&val);if(val>kminheap[0]){kminheap[0]=val;AdjustDown(kminheap, k, 0);}}for(int i=0;i<k;i++){printf("%d ",kminheap[i]);} } int main() {//CreatData();PrintTopk(5);return 0; }
🌸🌸🌸如果大家还有不懂或者建议都可以发在评论区,我们共同探讨,共同学习,共同进步。谢谢大家! 🌸🌸🌸
相关文章:

C语言数据结构——树、堆(堆排序)、TOPK问题
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章,「初学」C,数据结构 🔥座右铭:“不要等到什么都没…...
springboot+vue 刘老师
课程内容 前端:vue elementui 后端:springboot mybatisplus 公共云部署 ------boot-------- 热部署 不用devtools,交给jrebel工具 RequestMapping 参数 value 路径 method 方法consumes 请求媒体类型 如 application/jsonproduces …...

学生网上考试报名系统的设计与实现
技术栈: MySQL、Maven、SpringBoot、Spring、SpringMVC、MyBatis、HikariCP、fastjson、slf4j系统功能:用户角色: (1)登录:用户在登录界面输入正确的账户名和密码,点击登录,系统将与…...

Jmeter实现分布式并发
Jmeter实现分布式并发,即使用远程机执行用例。 环境: VMware Fusion Windows系统是win7。 操作过程 1、Master在jmeter.properties添加remote_hosts 2、Slave在jmeter.properties添加server_port 同时把remote_hosts修改为和主机(Master…...

动态xml文件配置 hibernate validator 约束校验
父文章 入参校验产品化 schema_个人渣记录仅为自己搜索用的博客-CSDN博客 一般都是通过 注解进行校验, 很少看到 通过配置来进行校验. 自己再通过谷歌找到了官网文档hibernate validator constraint from xml Hibernate Validator 8.0.0.Final - Jakarta Bean Validation Re…...
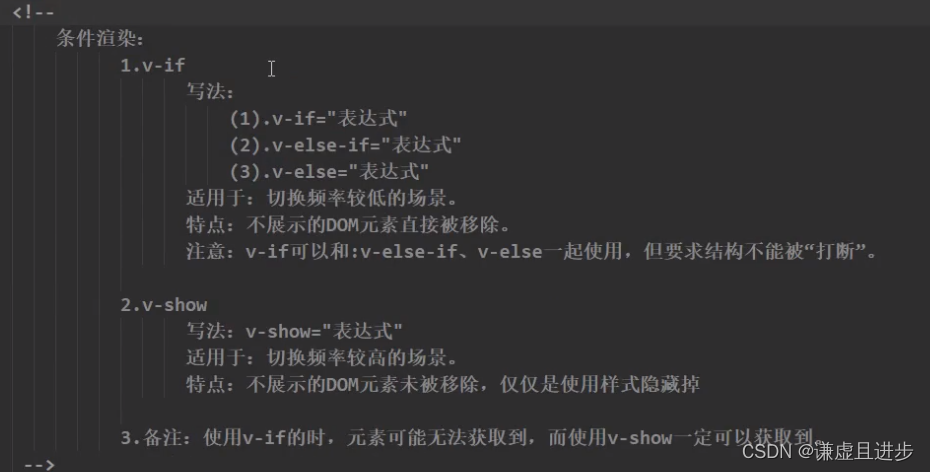
Vue绑定class样式与style样式
1,回顾HTML的class属性 答:任何一个HTML标签都能够具有class属性,这个属性可能只有一个值,如class"happs",也有可能存在多个属性值,如class"happs good blue",js的原生DOM针…...
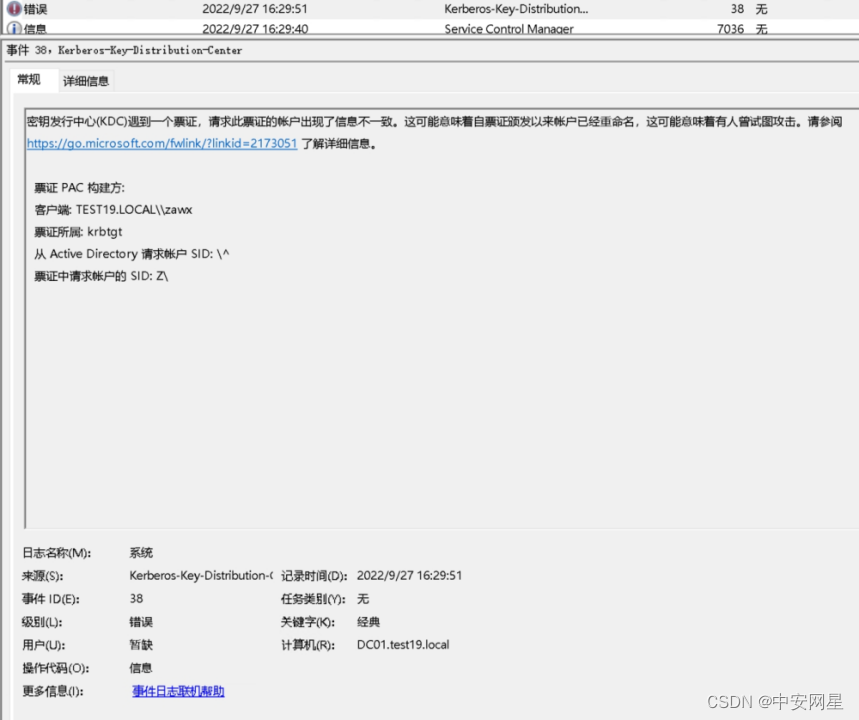
集权攻击系列:如何利用PAC新特性对抗黄金票据?
黄金票据简介 黄金票据是一种常见的域内权限维持手段,这种攻击主要是利用了Kerberos认证过程中TGT票据由KRBTGT用户的hash加密的特性,在掌握KRBTGT用户密码之后可以通过签发一张高权限用户的TGT票据,再利用这个TGT向KDC获取域内服务的ST来实…...
(未完全解析))
同程面试(部分)(未完全解析)
一面 Java直接内存有了解吗?为什么Java NIO的效率更高?Netty用到很多NIO,来了一个请求后Netty是怎么分发的,它里面有哪些角色?粘包、拆包怎么解决?为什么建立TCP连接是三次握手,而不是四次&…...

讯飞星火_VS_文心一言
获得讯飞星火认知大模型体验授权,第一时间来测试一下效果,使用申请手机号登录后,需要同意讯飞SparkDesk体验规则,如下图所示: 同意之后就可以进行体验了,界面如下: 讯飞星火效果体验 以下Promp…...

Java的集合
1. HashMap排序题,上机题。 已知一个HashMap<Integer,User>集合, User有name(String)和age(int)属性。请写一个方法实现对HashMap 的排序功能,该方法接收 HashMap<Intege…...

addr2line 使用,定位kernel panic 代码位置
在kernel崩溃时,方便定位代码。 需要打开kernel配置CONFIG_DEBUG_INFO。 需要有System.map和vmlinux文件,一般在out目录。 一般panic的时候会有给出panic的指针,如下down_write。 el1_data说明发生异常了,进入和entry.S文件&a…...

OpenAI目前所有模型介绍
目录 概述 GPT-4 (limted beta) GPT-3.5 GPT-3 各类模型介绍 DALLE Beta Whisper Beta Embeddings Moderation Codex (deprecated) 概述 模型描述GPT-4 Limited beta 一组在 GPT-3.5 上改进的模型,可以理解并生成自然语言或代码GPT-3.5一组在 GPT-3 上改…...

【P43】JMeter 吞吐量控制器(Throughput Controller)
文章目录 一、吞吐量控制器(Throughput Controller)参数说明二、测试计划设计2.1、Total Executions2.2、Percent Executions2.3、Per User 一、吞吐量控制器(Throughput Controller)参数说明 允许用户控制后代元素的执行的次数。…...

方正书版命令详解
方正书版常用的排版符包括: 空格:表示文字之间的间距,不同字号的文字需要适当调整空格大小。 省略号:用于省略一段文字,通常用三个点表示(…)。 破折号:用于表示强调或者断句&…...
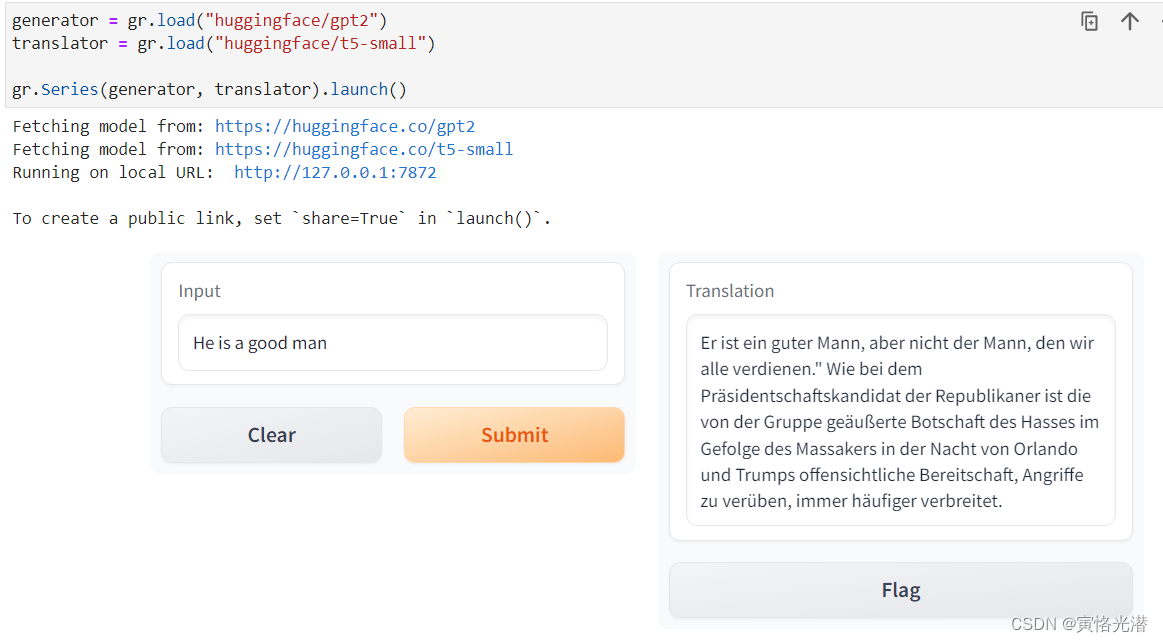
Gradio的web界面演示与交互机器学习模型,高级接口特征《6》
大多数模型都是黑盒,其内部逻辑对最终用户是隐藏的。为了鼓励透明度,我们通过简单地将Interface类中的interpretation关键字设置为default,使得向模型添加解释变得非常容易。这允许您的用户了解输入的哪些部分负责输出。 1、Interpret解释 …...
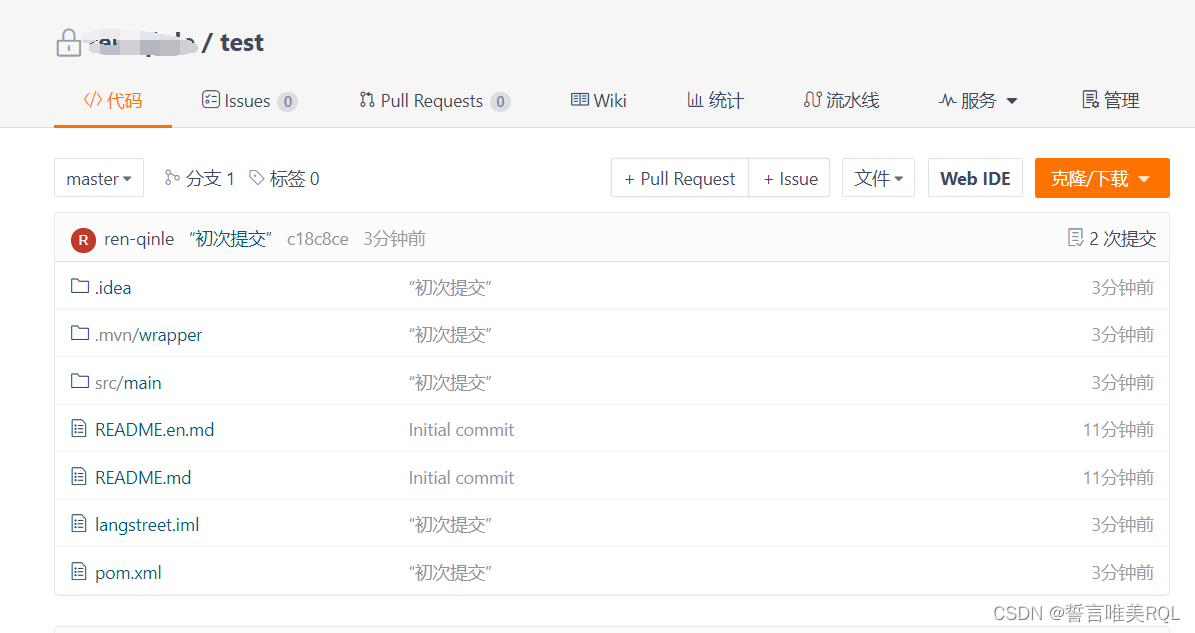
本地项目上传到Git(Gitee)仓库
一、步骤解答(详细图解步骤见第二大点) 1、打开我们的项目所在文件夹,我们发现是不存在.git文件 2、在你的项目文件夹外层【鼠标右击】弹出菜单,在【鼠标右击】弹出的菜单中,点击【Git Bash Here】,弹出运…...

Android 12.0屏蔽掉SystemUI的某些通知提示音
1.概述 在12.0的系统开发中,在系统SystemUI中会发一些通知的声音,但是同时也会在开机的时候,会有一些通知的声音,特别是不想要的一些通知的声音, 这些对于产品还是有一些影响的,所以为了产品体验,就需要屏蔽掉一些开机的通知的声音 2.屏蔽某些通知的提示音的核心代码 …...

测试计划模板二
XXX测试计划 文档作者: 编写日期: 项目经理: 批准日期: 文档模板修改纪录表 日期 修改人 修改内容描述...

华为OD机试真题B卷 Java 实现【分奖金】,附详细解题思路
一、题目描述 公司老板做了一笔大生意,想要给每位员工分配一些奖金,想通过游戏的方式来决定每个人分多少钱。按照员工的工号顺序,每个人随机抽取一个数字。按照工号的顺序往后排列,遇到第一个数字比自己数字大的,那么…...
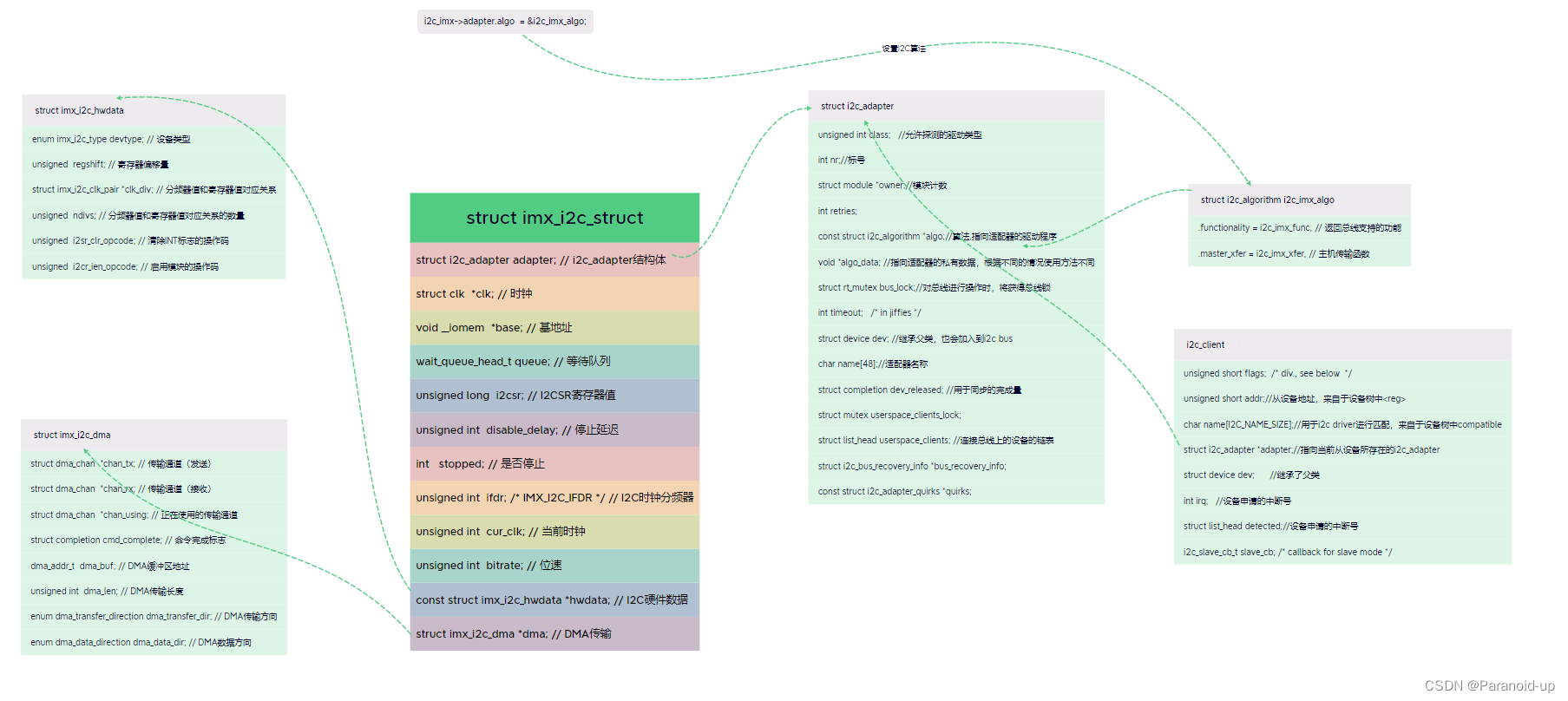
IMX6ULL平台I2C数据结构分析
IMX6ULL平台I2C数据结构分析 文章目录 IMX6ULL平台I2C数据结构分析i2c_clienti2c_adapterimx_i2c_structimx_i2c_hwdataimx_i2c_dma 在 i.MX 平台的 I2C 驱动中,存在多个相关的结构体,它们之间的联系和在内核中的作用如下: struct i2c_client…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...