【刷题之路】LeetCode 面试题 03.02. 栈的最小值
【刷题之路】LeetCode 面试题 03.02. 栈的最小值
- 一、题目描述
- 二、解题
- 1、方法1——“辅助栈”
- 1.1、思路分析
- 1.2、代码实现
一、题目描述
原题连接: 面试题 03.02. 栈的最小值
题目描述:
请设计一个栈,除了常规栈支持的pop与push函数以外,还支持min函数,该函数返回栈元素中的最小值。执行push、pop和min操作的时间复杂度必须为O(1)。
示例:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
二、解题
1、方法1——“辅助栈”
1.1、思路分析
既然题目应经明确要求了,min操作的时间复杂度必须为O(1),那我们想用遍历的方法来找到最小值的想法也就不现实了,那我们应该怎样解决这个O(1)的问题呢?
我们可以借助一个辅助的栈minStack,来存储当前栈中最小的值当我们每次执行push时候,就相应的将当前栈中最小的值也入到minStack中。即minStack的栈顶元素就是当前栈中最小的值:

具体的操作是:
1、当栈为空时,统一将新压入栈的元素压入到Stack和minStack。
2、当栈不为空时,如果新压入栈的元素小于minStack栈顶的元素,就将新的元素压入minStack中,否则则继续将minStack的栈顶元素压入minStack。
然后当我们要执行min操作时,就直接返回minStack的栈顶元素及可。
而当我们执行Pop弹栈操作时,则需要让Stack和minStack同步弹栈,以确保在任何情况下minStack的栈顶元素都为Stack中的最小值。
有的朋友可以会有疑问:难道要在栈中再嵌套定义一个子栈,然后执行各项操作的时候同时对这个子栈在执行相应的接口?
其实么这个必要,我们只需要在栈中额外定义一个存储结构来存储当前栈中的最小值即可。就比如我们选用数组来实现栈,那我们就再额外定义一个数组来存储栈中的最小值,比如下面这样:
typedef struct {int *data;int size; // 当前栈中的数据个数int capacity; // 当前栈的容量int *minStack; // 数组模拟一个栈,存储对应的最小值
} MinStack;
然后其实size和capacity是可以被data和minStack共用的,因为它们是同步Push和Pop操作的。
1.2、代码实现
有了以上思路,那我们写起代码来也就水到渠成了:
初始化工作:
typedef struct {int *data;int size;int capacity;int *minStack; // 数组模拟一个栈,存储对应的最小值
} MinStack;MinStack* minStackCreate() {MinStack *stack = (MinStack*)malloc(sizeof(MinStack));if (NULL == stack) {perror("malloc fail!\n");exit(-1);}stack->data = NULL;stack->minStack = NULL;stack->size = 0;stack->capacity = 0;return stack;
}
压栈接口Push:
因为data和minStack是同并且共用size和capacity的,所以在增容时候也需要同步增容data和minStack。
void minStackPush(MinStack* obj, int x) {// 先检查是否需要增容if (obj->size == obj->capacity) {int newCapacity = obj->capacity == 0 ? 10 : 2 * obj->capacity;int *temp1 = (int*)realloc(obj->data, newCapacity * sizeof(int));if (NULL == temp1) {perror("realloc fail!\n");exit(-1);}int *temp2 = (int*)realloc(obj->minStack, newCapacity * sizeof(int));if (NULL == temp2) {perror("realloc fail!\n");exit(-1);} obj->data = temp1;obj->minStack = temp2;obj->capacity = newCapacity;}if (obj->size == 0) {obj->minStack[obj->size] = x;} else {int min = x < obj->minStack[obj->size - 1] ? x : obj->minStack[obj->size - 1];obj->minStack[obj->size] = min;}obj->data[obj->size] = x;obj->size++;
}
弹栈Pop接口:
void minStackPop(MinStack* obj) {assert(obj->size != 0);obj->size--;
}
取栈顶Top接口:
int minStackTop(MinStack* obj) {assert(obj->size != 0);return obj->data[obj->size - 1];
}
求最小值min接口:
int minStackGetMin(MinStack* obj) {assert(obj->size != 0);return obj->minStack[obj->size - 1];
}
释放free接口:
void minStackFree(MinStack* obj) {free(obj->data);free(obj->minStack);obj->data = NULL;obj->minStack = NULL;obj->size = 0;obj->capacity = 0;
}
相关文章:

【刷题之路】LeetCode 面试题 03.02. 栈的最小值
【刷题之路】LeetCode 面试题 03.02. 栈的最小值 一、题目描述二、解题1、方法1——“辅助栈”1.1、思路分析1.2、代码实现 一、题目描述 原题连接: 面试题 03.02. 栈的最小值 题目描述: 请设计一个栈,除了常规栈支持的pop与push函数以外&am…...

如何处理图片排重(精准排重,相似排重)
图片相似度对比 1、需求 假如有一个图片池,存有1亿图片。给一张目标图片,在图片池中做匹配。 判断一张图片是否在图片池中出现过。(完全一样)判断有没有相似的出现过。比如两张图相似度90,两张图片是在描述一件事情。 …...

盐城北大青鸟“北大青鸟杯”IT精英挑战赛设中心评审隆重开赛
为积极响应北大青鸟总部开展第十届“北大青鸟杯”全国IT精英挑战赛的号召,成就学员们的IT梦想,“北大青鸟杯”IT精英挑战赛(设计组)盐城卓晨中心评审于2023年5月25日下午1:00在人才大厦306教室正式开赛! 赛前&a…...
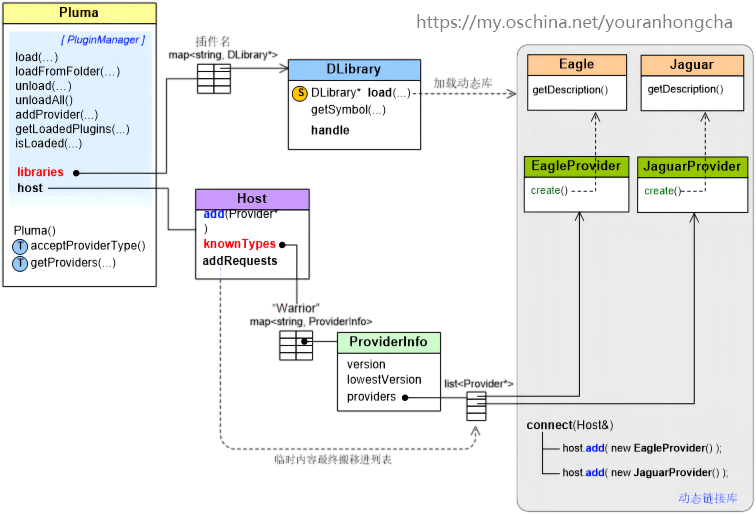
Pluma 插件管理框架
1. 概述 Pluma 是一个用 C 开发的可用于管理插件的开源架构,其官网地址为:http://pluma-framework.sourceforge.net/。该架构是个轻量级架构,非常易于理解。 Pluma 架构有以下基本概念: 1)插件的外在行为体现为一个…...
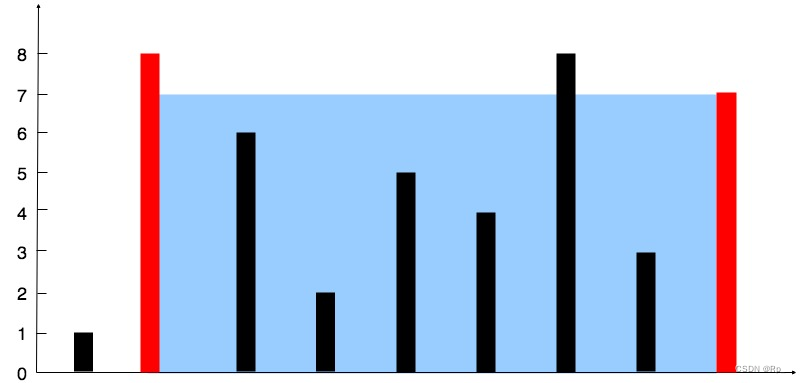
Leetcode11 盛最多水的容器
Leetcode11 盛最多水的容器 来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/container-with-most-water/description 博主Github:https://github.com/GDUT-Rp/LeetCode 题目: 给定一个长度为 n…...

Java
FileOutputStream写数据的3种方式 void write(int b) //一次写一个字节的数据 void write(byte[] b) //一次写一个字节数组数据 void write(byte[] b, int off,int len) //一次写一个字节数组的部分数据 参数一:数组;参数二:起始索引 0;参数三:个数换行: windows:“\r\n” lin…...
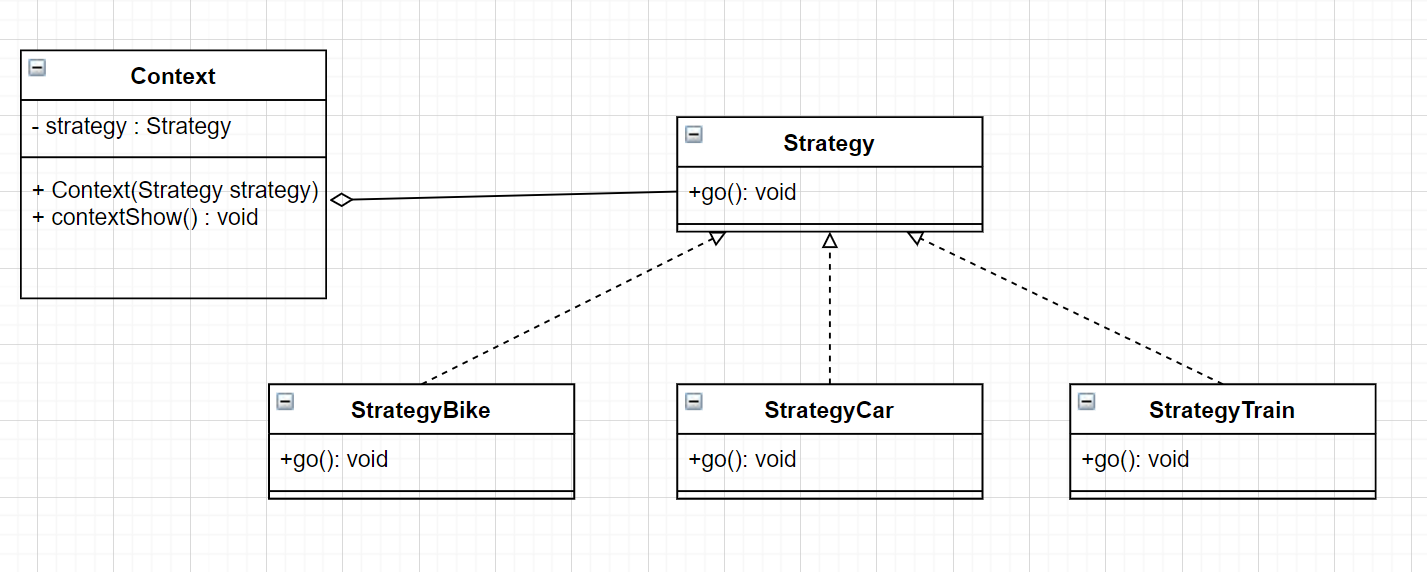
第十四章行为性模式—策略模式
文章目录 命令模式解决的问题结构实例存在的问题适用场景 JDK源码解析 行为型模式用于描述程序在运行时复杂的流程控制,即描述多个类或对象之间怎样相互协作共同完成单个对象无法单独完成的任务,它涉及算法与对象间职责的分配。行为型模式分为类行为模式…...
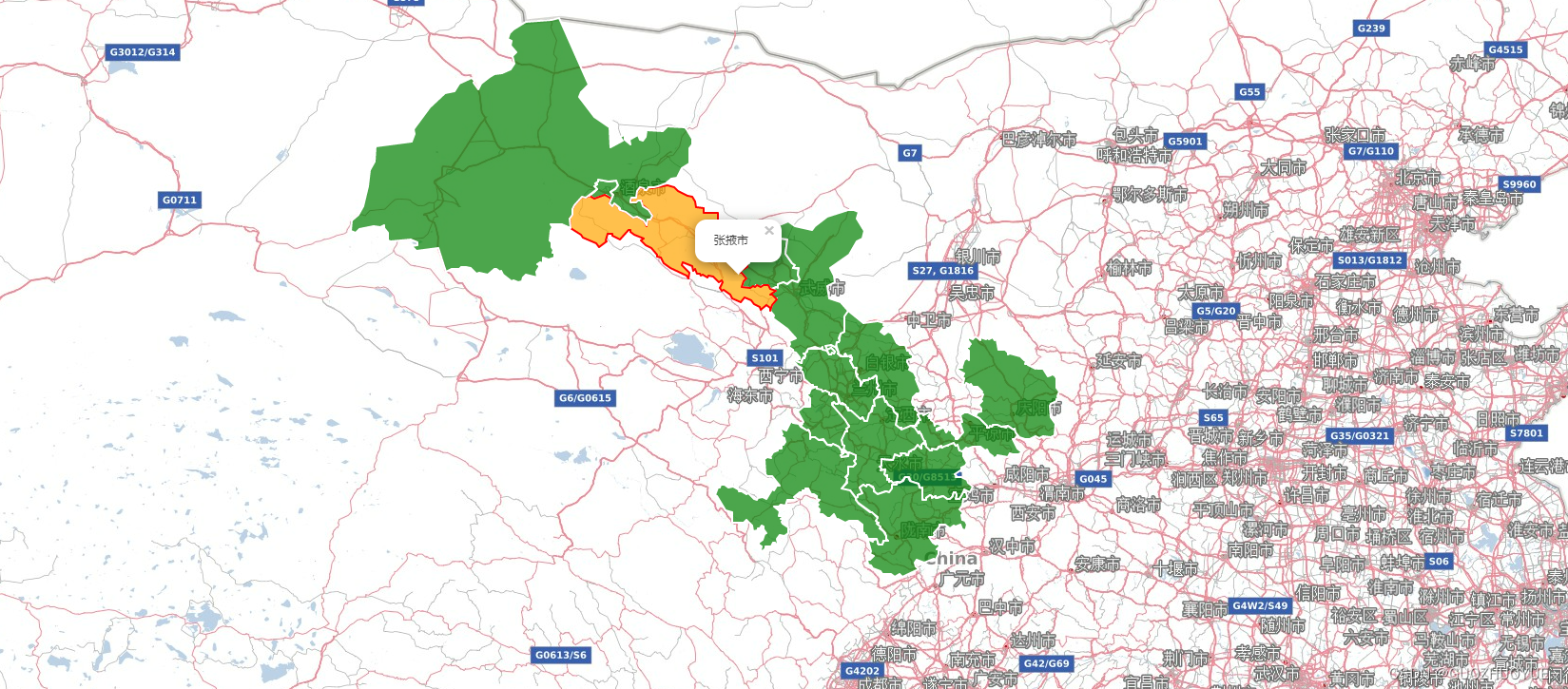
Leaflet基本用法
使用 阿里云地理工具 获取相应的地理JSON数据,用于对地图边界绘制。 如何使用leaflet? 这里用HTML5进行操作; 因为我是用的是Leaflet库,所以要引入JavaScript 和 CSS 文件(可参考官网https://leafletjs.com/&#x…...
Unity | HDRP高清渲染管线学习笔记:示例场景解析
目录 一、HDRP入门 1.HDRP设置 1.1 HDRP配置文件中的全部设置项 1.1.1 Rendering下的Lit Shader Mode 1.1.2 Lighting 下的Volumetrics(体积光)和Screen Space Reflection(屏幕空间反射) 2.离线渲染VS实时渲染 3.Volume组件 …...
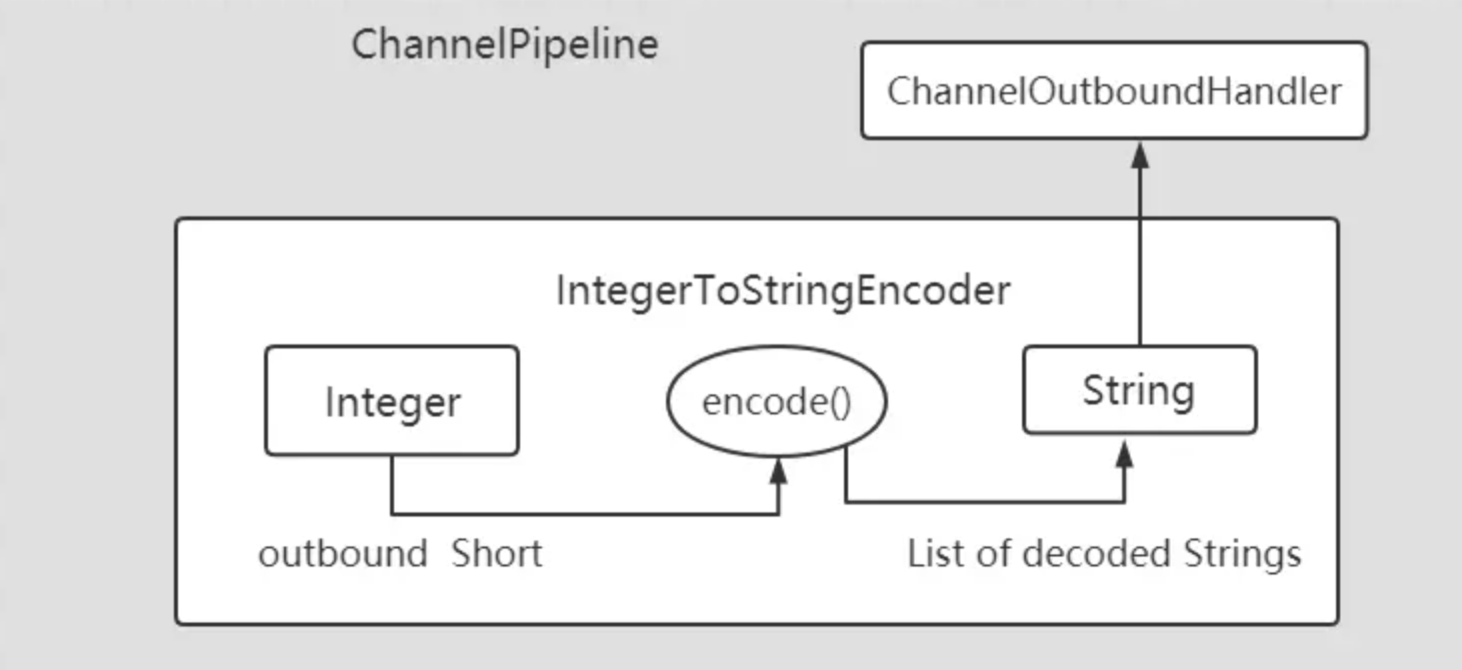
【Netty】Netty 编码器(十三)
文章目录 前言一、MessageToByteEncoder 抽象类二、MessageToMessageEncoder 抽象类总结 前言 回顾Netty系列文章: Netty 概述(一)Netty 架构设计(二)Netty Channel 概述(三)Netty ChannelHan…...

Netty和Tomcat的区别、性能对比
文章目录 一、Netty和Tomcat有什么区别?二、为什么Netty受欢迎?三、Netty为什么并发高 ? 一、Netty和Tomcat有什么区别? Netty和Tomcat最大的区别就在于通信协议,Tomcat是基于Http协议的,他的实质是一个基…...

chatgpt赋能python:Python函数调用局部变量-深入了解
Python函数调用局部变量-深入了解 函数调用局部变量是Python中的一个重要概念,特别是在大型项目中,其中多个函数共享相同变量时。在本文中,我们将深入探讨Python函数调用局部变量,并为您介绍一些实用技巧。 什么是Python函数调用…...

Android 12.0 NavigationBarView 导航栏 左边显示的修改
1.概述 在12.0定制化开发中,要求导航栏左边显示的定制化,这时需要了解导航栏的显示控制方向,然后修改显示方向 在10.0以后关于导航栏显示位置都是在DisplayPolicy.java中处理的所以查询相关的设置方法,然后修改导航栏显示方向2.NavigationBarView 导航栏 左边显示的修改的…...

Mybatis源码细节探究:二级缓存Cache对象是在什么时候创建的?
给自己的每日一句 不从恶人的计谋,不站罪人的道路,不坐亵慢人的座位,惟喜爱耶和华的律法,昼夜思想,这人便为有福!他要像一棵树栽在溪水旁,按时候结果子,叶子也不枯干。凡他所做的尽…...

【数据库】无效数据:软件测试对无效数据的处理
目录 一、无效数据的常见场景 (1)测试阶段 (2)测试方法 二、无效数据的概念 三、无效数据的影响 四、无效数据的识别 五、无效数据的处理方法 (1)拒绝无效数据 ① 拒绝无效数据的概念 ② 拒绝…...

高精度电压源如何设计出来的
高精度电压源是一种用于提供高精度电压的电子设备,通常用于测量和控制系统。高精度电压源的设计是一个复杂的过程,需要考虑多个因素,包括电路设计、元件选型、测量误差、稳定性等。下面将从电路设计和元件选型两个方面,详细介绍高…...

混合属性mix-blend-mode不生效
下面的ABCDE是混合图层,box是他们的父级,一般浏览器支持都没什问题需要注意的是,确保父元素不是透明的, 我使用的时候发现给父元素rgba设置透明度这种方式没啥作用,还得是纯色,没去深究,设置纯色…...

测试计划编写说明
第1章 引言 1.1目的 简述本计划的目的,旨在说明各种测试阶段任务、人员分配和时间安排、工作规范等。 测试计划在策略和方法的高度说明如何计划、组织和管理测试项目。测试计划包含足够的信息使测试人员明白项目需要做什么是如何运作的。另外,清晰的文档结构能使任何一个读…...

Android 12.0Recent列表不显示某个app
1.概述 在12.0 的产品定制化开发中,在点击导航栏最近任务列表时,如果做到不显示某个app 呢 一种做法是在app中直接处理 一种做法是在framework中处理 接下来看这两种处理方法 1, app中处理 为该应用AndroidManifest xml文件中主MainActivity设置属性 android:excludeFromR…...

力扣sql中等篇练习(二十七)
力扣sql中等篇练习(二十七) 1 连续两年有3个及以上订单的产品 1.1 题目内容 1.1.1 基本题目信息 1.1.2 示例输入输出 1.2 示例sql语句 # Write your MySQL query statement below WITH T as (SELECT t.product_id,t.d,count(order_id) numFROM(SELECT order_id,product_id,…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
