【线性规划模型】
线性规划模型:原理介绍和预测应用
引言
线性规划是运筹学中一种重要的数学优化方法,被广泛应用于各个领域,包括工业、经济、物流等。
线性规划模型的原理
线性规划模型的目标是在一组线性约束条件下,寻找一组变量的最优解,使得目标函数达到最大或最小。线性规划模型可以用以下形式表示:
max/min Z = c1x1 + c2x2 + ... + cnxn
subject to:
a11x1 + a12x2 + ... + a1nxn <= b1
a21x1 + a22x2 + ... + a2nxn <= b2
...
am1x1 + am2x2 + ... + amnxn <= bm
x1, x2, ..., xn >= 0
其中,Z是目标函数,c1, c2, …, cn是目标函数的系数,x1, x2, …, xn是决策变量,a11, a12, …, amn是约束条件的系数,b1, b2, …, bm是约束条件的边界值。
线性规划模型的解可以通过线性规划算法来获得,例如单纯形法、内点法等。这些算法通过不断迭代改进解的质量,直到达到最优解。
实战:销售决策问题
假设一家电子产品制造商生产两种产品:手机和平板电脑。该公司的目标是最大化利润。每个手机的利润为$20,每个平板电脑的利润为$30。该公司的生产能力有限,每天只能生产100个手机和80个平板电脑。此外,该公司还需要满足市场需求,每天至少需要生产60个手机和40个平板电脑。我们的目标是确定生产多少手机和平板电脑才能实现最大利润。
首先,我们定义决策变量:
- x1:生产的手机数量
- x2:生产的平板电脑数量
其次,我们可以设置目标函数和约束条件:
max Z = 20x1 + 30x2
subject to:
x1 <= 100
x2 <= 80
x1 >= 60
x2 >= 40
x1, x2 >= 0
接下来,我们可以使用Python中的线性规划库来求解这个问题。下面是使用PuLP库的代码示例:
from pulp import *# 创建问题
problem = LpProblem("Sales Decision", LpMaximize)# 定义决策变量
x1 = LpVariable("x1", lowBound=0)
x2 = LpVariable("x2", lowBound=0)# 定义目标函数
problem += 20*x1 + 30*x2, "Objective"# 定义约束条件
problem += x1 <= 100
problem += x2 <= 80
problem += x1 >= 60
problem += x2 >= 40# 求解问题
status = problem.solve()# 打印结果
print(f"Status: {LpStatus[status]}")
print(f"Optimal Solution: x1 = {value(x1)}, x2 = {value(x2)}")
print(f"Maximum Profit: ${value(problem.objective)}")
运行代码后,我们可以得到以下结果:
Status: Optimal
Optimal Solution: x1 = 100.0, x2 = 80.0
Maximum Profit: $4400.0

这意味着,在生产100个手机和80个平板电脑时,该公司可以实现最大利润为$4400。
lingo代码更为简单:
model:max = 20*x1 + 30*x2;x1 <= 100;x2 <= 80;x1 >= 60;x2 >= 40;
end
结论
线性规划模型可以应用于各个领域的决策问题。通过定义目标函数和约束条件,我们可以使用线性规划算法来求解最优解。
参考文献:
- Wikipedia - Linear programming
相关文章:

【线性规划模型】
线性规划模型:原理介绍和预测应用 引言 线性规划是运筹学中一种重要的数学优化方法,被广泛应用于各个领域,包括工业、经济、物流等。 线性规划模型的原理 线性规划模型的目标是在一组线性约束条件下,寻找一组变量的最优解&…...

android 12.0卸载otg设备开机不加载otg设备
1.概述 在12.0定制化开发过程中,客户有功能需求,通过系统属性值控制是否加载挂载otg设备,当设置为卸载模式时,要求不能挂载otg设备,开机也不能挂载otg设备 2.卸载otg设备开机不加载otg设备的核心代码 frameworks/base/services/core/java/com/android/server/StorageMan…...

通过 Wacom 的 Project Mercury 提高远程办公效率
过去几年中,我们的工作方式发生了翻天覆地的变化。疫情加快了对远程办公和协作的采纳,导致人们更加依赖技术来联系团队和提高工作效率。 但是,那些依靠专门硬件和软件来完成工作的创作者呢?艺术家、设计师和开发人员需要使用专门…...
Linux-0.11 文件系统namei.c详解
Linux-0.11 文件系统namei.c详解 模块简介 namei.c是整个linux-0.11版本的内核中最长的函数,总长度为700行。其核心是namei函数,即根据文件路径寻找对应的i节点。 除此以外,该模块还包含一些创建目录,删除目录,创建目…...
计算机网络学习笔记
<!-- GFM-TOC --> 计算机网络体系结构 传输层:TCP和UDP 什么是三次握手? 什么是四次挥手? TCP如何实现流量控制? TCP的拥塞控制是怎么实现的? TCP如何最大利用带宽? TCP与UDP的区别 TCP如何保…...

Pod相关操作命令
Pod相关操作命令 Pod setup # CocoaPods 将信息下载到~/.cocoapods/repos 目录下。如果安装 CocoaPods 时不执行此命令,在初次执行pod intall 命令时,系统也会自动执行该指令 pod --version # 检查 CocoaPods 是否安装成功及其版本号 pod repo update #…...
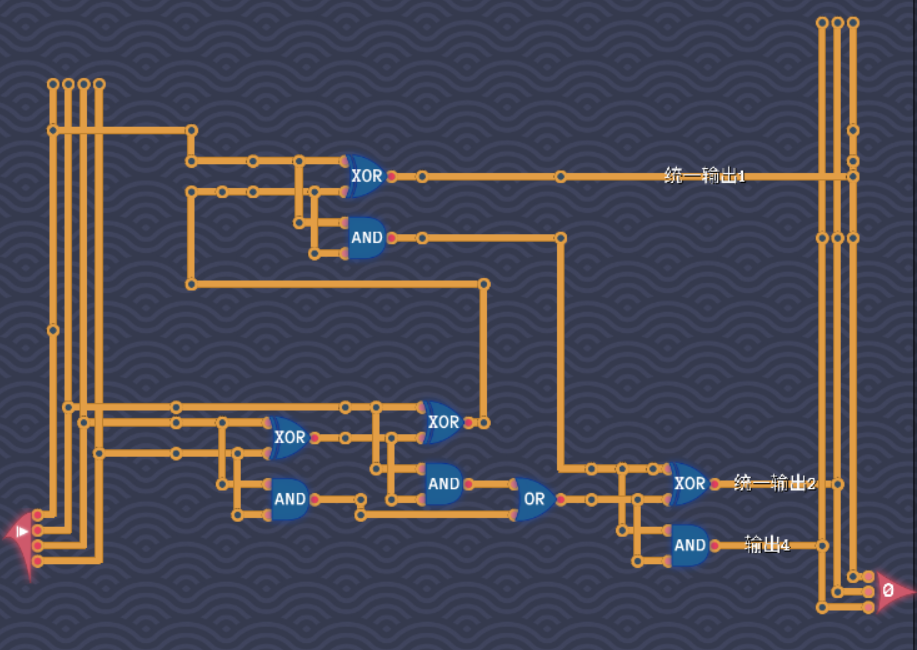
图灵完备游戏:信号计数 解法记录
使用1个全加器 2个半加器完成。这关的思想主旨在于如何把输出4,输出2,输出1的情况统一在一根导线上。 首先用一个全加器来完成输入2-4这三个引脚的计数,因为全加器输出范围二进制是00 - 11,而输入正好有两个引脚数位是2和1&…...

数据结构图的基础概念
1、图的概念 图(Graph):是由顶点的有穷非空集合和顶点之间边的集合组成。顶点(Vertex):图中的数据元素。边(Edge):顶点之间的逻辑关系,边可以是有向的或无向的,也可以带有权重(可以表示距离,花费等…...

一场九年前的“出发”:奠基多模态,逐鹿大模型
原创:谭婧 全球AI大模型的技术路线,没有多少秘密,就那几条路线,一只手都数得过来。 而举世闻名的GPT-4浑身上下都是秘密。 这两件事并不矛盾。为什么呢? 这就好比,回答“如何制造一台光刻机?”。…...

什么是url跳转漏洞?
什么是url跳转漏洞 简介原因:如何防止 简介 URL跳转漏洞是一种Web应用程序安全问题,指的是在应用程序处理URL跳转时,由于程序员的疏忽或设计不当,攻击者可能通过构造恶意URL来实现对应用程序的攻击。 原因: 跳转条件…...

生物学经典blast比对算法,R语言和Python如何实现?
Blast比对算法原理与实现方式 做生物的同学肯定听说过blast比对这个方法,一般在NCBI等网站上可以在线进行比对,也可以在本地服务器进行比对,那么blast算法究竟是怎么实现对不同序列的比对呢? 本文分享经典blast算法的基础原理&…...

Android 开机动画支持mp4格式视频播放
前 言 Android系统在启动的过程中,最多可以出现三个画面,每一个画面都用来描述一个不同的启动阶段。无论是哪一个画面,它们都是在一个称为帧缓冲区(frame buffer,简称fb)的硬件设备上进行渲染的。 自定义…...

软考A计划-试题模拟含答案解析-卷十
点击跳转专栏>Unity3D特效百例点击跳转专栏>案例项目实战源码点击跳转专栏>游戏脚本-辅助自动化点击跳转专栏>Android控件全解手册点击跳转专栏>Scratch编程案例 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&am…...

Kafka入门(安装和SpringBoot整合)
文章目录 一、Docker安装Kafka1. 创建网络2. 安装zookeeper3. 安装Kafka 二、Kafka介绍1. Kafka简介 三、SpringBoot整合Kafka1. 引入pom依赖2. application.propertise配置3. Hello Kafka(Producer)4. Consumer Kafka5. 带回调的生产者6. 自定义分区器7. kafka事务提交8. 指定…...

gitLab相关命令
gitLab相关命令 1) 远程仓库相关命令 git clone 远程仓库地址 #检出仓库git remote -v #查看远程仓库git remote add [name][url] #添加远程仓库,git remote add origin 远程仓库地址git remote rm [name] #删除远程仓库,git remote rm origingit remo…...

一些查看日志时的常用命令
文章目录 1、grep -r 搜索内容 *2、l * 关键字 *3、tail -f 文件名4、tail -n X 文件名5、cat 文件名 | grep "关键字" -C X同理可得,-A同理可得,-B 一些查看日志时的常用命令 1、grep -r 搜索内容 * 作用:在一堆文件里࿰…...
和作用域(scope)及垃圾回收)
Javascript 的执行环境(execution context)和作用域(scope)及垃圾回收
执行环境有全局执行环境和函数执行环境之分,每次进入一个新执行环境,都会创建一个搜索变量和函数的作用域链。函数的局部环境不仅有权访问函数作用于中的变量,而且可以访问其外部环境,直到全局环境。全局执行环境只能访问全局执行…...

CRDT协同算法
CRDT的英文全称是Conflict-free Replicated Data Type,最初是由协同文本编辑和移动计算而发展的,现在还被用作在线聊天系统、音频分发平台等等。当前CRDT算法在富文本编辑器领域的协同依旧是典型的场景,常用于作为实现文档协同的底层算法&…...

近代中国的三次思想文化运动
1、戊戌变法中维新派顽固派论战 第一次思想解放潮流是1898年维新派与顽固势力的论战。论战的内容有:要不要变法,要不要兴民权、实行君主立宪,要不要提倡西学、改变教育制度。此次论争是资本主义思想同封建主义思想的正面交锋,此后…...

《地铁上的面试题》--目录
第一部分:基础 数据结构与算法 1.1 数组和链表 1.2 栈和队列 1.3 树和图 1.4 排序和搜索算法 1.5 动态规划和贪心算法 操作系统 2.1 进程与线程 2.2 内存管理 2.3 文件系统 2.4 进程同步与通信 2.5 虚拟化和容器化技术 计算机网络 3.1 TCP/IP协议 3.2 HTTP和HTTPS…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
