cf1750E Bracket Cost
前言:
好久没训练了,来做道计数题找找感觉。**期末毁我青春
大意:
定义对于一个括号串 s的值,为通过最小次数以下操作使 s 实现括号匹配的操作次数。
- 选择一个子串,循环右移一位。
- 在任意一个位置插入一个任意括号。
求一个括号串的所有非空子串的值的和。
思路:
显然先分析对于一个串的情况
不难发现,操作1其实就是把子串的末尾提到前面,对于其它的字符不会有任何影响
我们令L表示串内左括号的数量,R表示右括号的数量,x表示串内已经匹配的括号对的数量
然后这里就有一个比较显然的操作思路:
假定L>=R,对于每一个没有匹配的左括号,如果我们能找到一个尚未匹配的右括号,则它一定在该左括号的前面,所以我们直接取以它们为端点的字串,执行操作1,这就实现了一个匹配。由于操作一只会对字串的端点产生影响,所以这不会破坏任何已有结构。如果这个左括号找不到尚未匹配的右括号,我们就直接执行操作2即可。
注意到每次操作都不会浪费,都达到了对应操作所能消去的最多的括号数,所以该操作是最优的,此时总操作次数是L-x
同理,R>=L时,总操作次数就是R-x
总结一下,对于一个字符串,其操作此时就是max{L,R}-1
所以我们得到答案就是
先求x
很套路地考虑每一个匹配的贡献,有多少个字串可以包含它。取左端点l,右端点r,则贡献就是l*(n-r+1),整体用一个栈就能实现匹配+求和的过程了
考虑max(L,R),可以做如下转化:,L+R的求和是比较简单的,就是类似于上一个的求法,考虑每一个位置的贡献。|L-R|,其实就是区间和的绝对值
取sum表示字符串的前缀和(左括号取1,右括号取-1),对sum排序之后(注意要把sum0也加进去)
不难发现这个的求和可以转化为
也就是
两部分求完之后除以2即可
整体时间复杂度nlogn
code
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
#define endl '\n'
const ll N=2e5+10;
ll n;
string s;
ll sum[N];
void solve()
{cin>>n;for(int i=0;i<=n+5;++i) sum[i]=0;cin>>s;s=" "+s;for(int i=1;i<=n;++i){if(s[i]=='(') sum[i]=sum[i-1]+1;else sum[i]=sum[i-1]-1;}sort(sum,sum+1+n);ll tot=0;for(int i=1;i<=n;++i) tot+=i*(n-i+1);for(int i=1;i<=n;++i) tot+=i*sum[i];for(int i=0;i<=n-1;++i) tot-=(n-i)*sum[i];tot/=2;//cout<<tot<<' ';stack<ll> st;for(int i=1;i<=n;++i){if(s[i]=='(') st.push(i);else{if(st.empty()) continue;int id=st.top();tot-=id*(n-i+1);st.pop();}}cout<<tot<<endl;
}
signed main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);ll t;cin>>t;while(t--)solve();return 0;
}相关文章:
cf1750E Bracket Cost
前言: 好久没训练了,来做道计数题找找感觉。**期末毁我青春 大意: 定义对于一个括号串 s的值,为通过最小次数以下操作使 s 实现括号匹配的操作次数。 选择一个子串,循环右移一位。在任意一个位置插入一个任意括号。 求一个括…...
Vue+springboot医院住院挂号登记收费系统7ui9s
医院信息管理系统的开发过程中,采用B / S架构,主要使用java语言进行开发,结合最新流行的springboot框架。使用Mysql数据库和idea开发环境。该医院信息管理系统包括用户、医生和管理员。其主要功能包括用户管理、医生管理、医生信息管理、预约…...

大前端之Koa2学习
Koa2框架介绍 Koa2是一个基于Node.js的Web框架,它使用了ES6的语法和async/await特性,使得编写异步代码更加简单和优雅。Koa2的核心思想是中间件,它允许开发者将应用程序拆分成小的、可重用的部分,从而使得代码更加模块化和易于维…...

Qml实现Dock浮动、停靠功能
纯Qml实现Dock浮动、停靠功能 效果展示github地址:介绍环境Demo代码参数说明API说明 效果展示 Qml Dock效果演示 github地址: https://github.com/longtwilight/QmlDock 介绍 这是一个使用纯qml实现的Dock组件,它支持停靠、浮动、窗体分离、窗体独立、大小调整等…...

最新版本 Stable Diffusion 开源 AI 绘画工具之微调模型篇
✨ 目录 🎈 模型种类🎈 变分自动编码器 / VAE🎈 美学梯度 / Aesthetic Gradients🎈 大型语言模型的低阶自适应 / LoRA🎈 超网络模型 / Hypernetwork🎈 微调模型 / LyCORIS 🎈 模型种类 当你打开…...

路径规划算法:基于哈里斯鹰优化的路径规划算法- 附代码
路径规划算法:基于哈里斯鹰优化的路径规划算法- 附代码 文章目录 路径规划算法:基于哈里斯鹰优化的路径规划算法- 附代码1.算法原理1.1 环境设定1.2 约束条件1.3 适应度函数 2.算法结果3.MATLAB代码4.参考文献 摘要:本文主要介绍利用智能优化…...
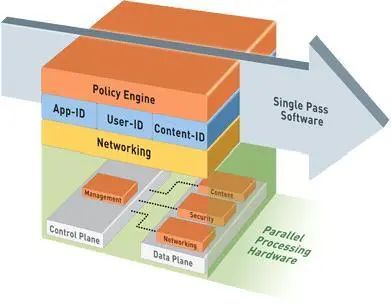
Web 应用程序防火墙 (WAF) 相关知识介绍
Web应用程序防火墙 (WAF) 如何工作? Web应用防护系统(也称为:网站应用级入侵防御系统。英文:Web Application Firewall,简称:WAF)。利用国际上公认的一种说法:Web应用防火墙是通过执…...

docker快速部署hue+hue集成hive
首先需要安装hive,hive的安装在HIVE的安装与配置_EEEurekaaa!的博客-CSDN博客 安装完成之后,使用脚本命令启动hdfs和hive的相关服务。 一、安装docker # 安装yum-config-manager配置工具 $ yum -y install yum-utils # 设置yum源 $ yum-co…...

基于java SpringBoot和Vue uniapp的校园信息交流小程序
随着信息社会的网络化和计算机科学的广泛普及和迅速普及应用,具有综合智能的我国校园信息教育网络已成为推动中小学科学教育及其实践科学发展的信息技术手段。迅速推进了信息化改革,改善了高校信息交流的网络环境,提高了信息教育平台的管理水…...

数据包伪造替换、会话劫持、https劫持之探索和测试
(一)数据包替换攻击 该攻击过程如下:伪造服务器响应客户端的数据包。监听客户端的数据包,用预先伪造的数据包,伪装成服务器返回的数据发送给客户端。 因为攻击者跟目标在同一个局域网,所以攻击者发送的数…...

正则表达式集合
目录 一、校验数字的表达式 1. 数字 2. n位的数字 3. 至少n位的数字 4. m-n位的数字 5. 零和非零开头的数字 6. 非零开头的最多带两位小数的数字 7. 带1-2位小数的正数或负数 8. 正数、负数、和小数 9. 有两位小数的正实数 10. 有1~3位小数的正实数 11. 非零的正整…...

Django框架中models对象转换为json的方法
在django框架中输出api接口时一般都是输出json数据但是通过orm获取的数据库数据一般都是object所以需要转换成json数据,一般有一下3种情况 1.models对象使用“all()”时 from django.http import HttpResponse from django.core import serializers from TestMode…...

利用Servlet编写第一个“hello world“
利用Servlet编写第一个"hello world" 🔎创建 Maven 项目🔎引入依赖🔎创建目录🔎编写代码🔎打包代码🔎部署🔎程序验证🔎结尾 🔎创建 Maven 项目 Maven 是一个构…...

python 爬虫之js逆向爬虫详解
随着网站前端技术的不断发展,越来越多的网站采用JS进行渲染,并加上了一些反爬机制,导致传统的爬虫技术有些力不从心。本文将为大家介绍如何进行JS逆向爬虫,并且不少于1000字。 一、JS逆向爬虫的介绍 JS逆向是一种分析反爬机制的…...

SpringBoot:WebSocket实现消息撤回、图片撤回
下面只是讲述一下实现思路,代码基本没有哈!有时间单独发表一篇关于websocket的相关操作的博客。 1. 消息撤回、图片撤回 个人觉得关于撤回,需要下述几个过程: 发送的消息的标签上可以定义一个属性,这个属性的值应该是…...

输出指定日期区间内的所有天、周、月
部分方法需要依赖hutool工具包。 <dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>4.5.10</version> </dependency>需求:输出2023-04-17到2023-05-23期间所有的天、周、月。…...

【线性规划模型】
线性规划模型:原理介绍和预测应用 引言 线性规划是运筹学中一种重要的数学优化方法,被广泛应用于各个领域,包括工业、经济、物流等。 线性规划模型的原理 线性规划模型的目标是在一组线性约束条件下,寻找一组变量的最优解&…...

android 12.0卸载otg设备开机不加载otg设备
1.概述 在12.0定制化开发过程中,客户有功能需求,通过系统属性值控制是否加载挂载otg设备,当设置为卸载模式时,要求不能挂载otg设备,开机也不能挂载otg设备 2.卸载otg设备开机不加载otg设备的核心代码 frameworks/base/services/core/java/com/android/server/StorageMan…...

通过 Wacom 的 Project Mercury 提高远程办公效率
过去几年中,我们的工作方式发生了翻天覆地的变化。疫情加快了对远程办公和协作的采纳,导致人们更加依赖技术来联系团队和提高工作效率。 但是,那些依靠专门硬件和软件来完成工作的创作者呢?艺术家、设计师和开发人员需要使用专门…...
Linux-0.11 文件系统namei.c详解
Linux-0.11 文件系统namei.c详解 模块简介 namei.c是整个linux-0.11版本的内核中最长的函数,总长度为700行。其核心是namei函数,即根据文件路径寻找对应的i节点。 除此以外,该模块还包含一些创建目录,删除目录,创建目…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
