【数据结构】第七周
目录
稀疏矩阵快速转置
三元组的矩阵加法
九宫格数独游戏
数组主元素
螺旋数字矩阵
蛇形矩阵
数组循环右移K位
稀疏矩阵快速转置【问题描述】 稀疏矩阵的存储不宜用二维数组存储每个元素,那样的话会浪费很多的存储空间。所以可以使用一个一维数组存储其中的非零元素。这个一维数组的元素类型是一个三元组,由非零元素在该稀疏矩阵中的位置(行号和列号对)以及该元组的值构成。而矩阵转置就是将矩阵行和列上的元素对换。 请你实现一个快速的对稀疏矩阵进行转置的算法。 (注意:我看到部分同学提交的代码是简单转置+排序,请务必修改为快速转置算法哦。) 【输入形式】 输入的第一行是两个整数r和c(r<200, c<200, r*c <= 12500),分别表示一个包含很多0的稀疏矩阵的行数和列数。接下来有r行,每行有c个整数,用空格隔开,表示这个稀疏矩阵的各个元素。 【输出形式】 输出为读入的稀疏矩阵的转置矩阵。输出共有c行,每行有r个整数,每个整数后输出一个空格。请注意行尾输出换行。 【样例输入】 6 7 【样例输出】 0 0 -3 0 0 15 【提示】 第二组测试数据行列较大,注意空间开大一点哦。 |
#include<iostream>
using namespace std;
int text[1000][1000];
#define MAX 10001struct tr{int row;int col;int e;
};
struct ts{tr data[MAX];int m,n,len;
};void create(ts &a,int x,int y)
{a.len=0;for(int i=0;i<x;i++){for(int j=0;j<y;j++){if(text[i][j]!=0){a.data[a.len].row=i;a.data[a.len].col=j;a.data[a.len].e=text[i][j];a.len++;}}}
}
void tran(ts &a,ts &b,int x,int y)
{int tmp,Col;int t=0;int num[1000]={0};int position[1000];for(int i=0;i<a.len;i++)num[a.data[i].col]++;position[0]=0;for(int i=1;i<y;i++){position[i]=position[i-1]+num[i-1];}for(int i=0;i<a.len;i++){Col=a.data[i].col;tmp=position[Col];b.data[tmp].row=a.data[i].col;b.data[tmp].col=a.data[i].row;b.data[tmp].e=a.data[i].e;position[Col]++; }for(int i=0;i<y;i++){for(int j=0;j<x;j++){if(b.data[t].row==i&&b.data[t].col==j){cout<<b.data[t].e<<" ";t++;}else{cout<<"0 ";}}cout<<endl;}
}
int main()
{ts a,b;int i,j,x,y;cin>>x>>y;for(i=0;i<x;i++){for(j=0;j<y;j++)cin>>text[i][j];}create(a,x,y);tran(a,b,x,y);
}
三元组的矩阵加法【问题描述】 以三元组表存储的稀疏矩阵A、B非零元个数分别为m和n。试编写程序,完成A+B。 【输入形式】 第一排为分别为A、B元素的个数,以下各排分别输入对应的三元组,头m组为A中的元素,接下来为B的元素,同一个矩阵的元素按照行递增排列,第一行规定为1,同一行的元素按照列递增排列,第一列规定为1 【输出形式】 为相应的三元组,以回车分开,如果结果全部为0,则输出 -1 -1 -1 【样例输入】 2 1 1 2 3 1 3 4 1 3 3 【样例输出】 1 2 3 1 3 7 | 40 |
#include<iostream>
#include<algorithm>
using namespace std;
typedef struct{int row,col;int e;
}matrix;
bool cmp(matrix x,matrix y)
{if(x.row<y.row) return 1;else if(x.row==y.row&&x.col<y.col) return 1;else return 0;
}
int main()
{matrix a[500],b[500];int x,y,cnt=0;cin>>x>>y;for(int i=0;i<x;i++)cin>>a[i].row>>a[i].col>>a[i].e;for(int i=0;i<y;i++)cin>>b[i].row>>b[i].col>>b[i].e;int k=x;for(int i=0;i<y;i++){int flag = 1,j;for(j=0;j<x;j++){if(a[j].row==b[i].row&&a[j].col==b[i].col){flag = 0;a[j].e+=b[i].e;}}if(flag){a[k].e=b[i].e;a[k].row=b[i].row;a[k++].col=b[i].col;}}sort(a,a+k,cmp);for(int i=0;i<k;i++){if(a[i].e!=0)cnt++;}if(cnt==0){cout<<"-1 -1 -1"<<endl;return 0;}else{for(int i=0;i<k;i++){if(a[i].e!=0)cout<<a[i].row<<" "<<a[i].col<<" "<<a[i].e<<endl;}}return 0;
}
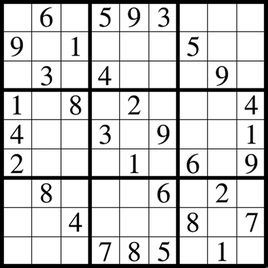
九宫格数独游戏【问题描述】
【输入形式】 【样例输出】 |
#include<iostream>
#include<cstring>
using namespace std;
int a[10][10];
bool row[10][10],col[10][10],g[10][10];void display()
{for(int i=1;i<=9;i++){for(int j=1;j<=9;j++)cout<<a[ i ][ j ]<<" ";cout<<endl;}
}
void dfs( int x ,int y)
{if(a[ x ][ y ] != 0){if( x == 9 &&y == 9)display();if( y == 9 )dfs( x + 1 , 1);elsedfs( x , y + 1 );}else{for( int i = 1 ; i <= 9 ; i++ ){if(row[x][i] && col[y][i] && g[(x-1)/3*3+(y-1)/3+1][i]){a[x][y] = i;row[x][i] = 0;col[y][i] = 0;g[(x-1)/3*3+(y-1)/3+1][i] = 0;if( x == 9 && y==9 )display();if( y==9 )dfs( x + 1, 1 );elsedfs( x , y + 1);a[x][y]=0;row[ x ][ i ]=1;col[ y ][ i ]=1;g[(x-1)/3*3+(y-1)/3+1][i]=1;}}}
}int main()
{memset(row,1,sizeof(row));memset(col,1,sizeof(col));memset(g,1,sizeof(g));for(int i=1;i<=9;i++){for(int j=1;j<=9;j++){cin>>a[i][j];if(a[i][j]>0){row[ i ][ a[i][j] ]=0;col[ j ][ a[i][j] ]=0;g[(i-1)/3*3+(j-1)/3+1][a[i][j]]=0;}}}dfs(1,1);return 0;
}
数组主元素【问题描述】这是一道2013年考研真题,已知一个整数序列A长度为N,其中若存在a,且a的个数大于N/2,则称a为A的主元素 例如:3 5 5 3 5 7 5 5,其主元素为5 又如:3 5 5 3 5 1 5 7,其中没有主元素。 假设元素保存在一个一维数组中,请设计一个尽可能高效的算法,找出主元素。若存在主元素则输出该元素否则输出 要求时间复杂度为O(N),请注意穷举法时间复杂度是O(N^2),排序再遍历查找的时间复杂度是O(N*logN+N) 【输入形式】 一个整数数组,以0作为结束输入 【输出形式】 主元素,若没有则输出-1 【样例输入】 3 5 5 3 5 7 5 5 0 【样例输出】 5 【样例说明】长度为8,共有5个‘5’ |
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{int a[100];int len=0,i=0;int sc;while(1){cin>>sc;if(sc==0) break;else a[i++]=sc;}len=i;
// for(int i=0;i<len;i++)
// cout<<a[i]<<" ";if(len==0) return 0;sort(a,a+len);
// cout<<endl;
// for(int i=0;i<len;i++)
// cout<<a[i]<<" ";int start=0,rail=0;int kk=a[len/2];for(int i=0;i<len;i++){if(a[i]==kk){start=i;break;}}for(int i=len-1;i>=0;i--){if(a[i]==kk){rail=i;break;}}
// cout<<endl<<start<<" "<<rail<<endl;int cnt=rail-start+1;if(cnt>(len/2)){cout<<kk;}else{cout<<"-1";}return 0;
}
螺旋数字矩阵
【问题描述】 编写一个程序,对任意输入的正整数n(n不大于10),产生并显示n阶螺旋式数字方阵。如n=3 要显示的方阵为
1 2 3
8 9 4
7 6 5
【输入形式】输入一个数n
【输出形式】产生n阶螺旋数字矩阵,数字以空格隔开
【样例输入】3
【样例输出】
1 2 3
8 9 4
7 6 5
【样例说明】注意输出的数字以空格隔开
#include<iostream>
#include<cstring>
using namespace std;
int dirx[4]={0,1,0,-1};
int diry[4]={1,0,-1,0};
int map[12][12];
int a[12][12];
int main()
{memset(map,sizeof(map),0);int n;cin>>n;for(int j=0;j<n+2;j++){map[0][j]=1;map[j][0]=1;map[n+1][j]=1;map[j][n+1]=1;}int num=n*n;int kk=1;a[1][1]=1;map[1][1]=1;int last=0;int i=1,j=1;while(--num){if(map[i+dirx[last]][j+diry[last]]==0){ i=i+dirx[last];j=j+diry[last];a[i][j]=++kk;map[i][j]=1;continue;}else{if(last==3) last=0;else last++;num++;continue;}}for(i=1;i<=n;i++){for(j=1;j<=n;j++)cout<<a[i][j]<<" ";cout<<endl;}} 蛇形矩阵【问题描述】蛇形矩阵是由1开始的自然数依次排列成的,按对角线方向依次递增 例如n=5时: 1 2 6 7 15 【输入形式】n 【输出形式】蛇形矩阵 【样例输入】5 【样例输出】 1 2 6 7 15 3 5 8 14 16 4 9 13 17 22 10 12 18 21 23 11 19 20 24 25 | 1.00 |
#include<bits/stdc++.h>
using namespace std;
int main()
{int a[20][20] = { 0 };int n = 0, m = 1;int i = 0, j = 0, flag = 0;cin>>n; while (m <= n * n){while (i >= 0 && (m <= n * n) && j <= n - 1){a[i][j] = m++;i--;j++;}flag++;if (flag < n)i++;else if (flag == n){i += 2;j--;}else{i += 2;j--;}while (j >= 0 && (m <= n * n) && i <= n - 1){a[i][j] = m++;i++;j--;}flag++;if (flag < n)j++;else if (flag == n){j += 2;i--;}else{i--;j += 2;}}for (int i = 0; i < n; i++){for (int j = 0; j < n; j++)printf("%d ", a[i][j]);cout<<endl;}return 0;
} 数组循环右移K位【问题描述】将一个数组中的元素循环右移K位,要求只使用一个元素大小的附加存储空间,时间复杂度为O(n)。 【样例输入】 1 2 3 4 5 6 7 8 0 2 【样例输出】 7 8 1 2 3 4 5 6 【提示】0代表输入结束 |
#include <iostream>
using namespace std;
void reverse(int start, int end, int a[], int temp)
{while (start < end){temp = a[start];a[start] = a[end];a[end] = temp;start++;end--;}
}
void move(int n, int len, int a[])
{//先把前len-step位逆置reverse(0, len - n - 1, a, a[len]);//再把后step位逆置reverse(len - n, len - 1, a, a[len]);//最后总体逆置reverse(0, len - 1, a, a[len]);
}
int main()
{ios::sync_with_stdio(false);int a[1000];int i = 0;while (1){cin >> a[i];if (a[i] == 0)break;i++;}int len = i;int step;cin >> step;step = step % len;move(step, len, a);for (int i = 0; i < len; i++)cout << a[i] << " ";
}相关文章:
【数据结构】第七周
目录 稀疏矩阵快速转置 三元组的矩阵加法 九宫格数独游戏 数组主元素 螺旋数字矩阵 蛇形矩阵 数组循环右移K位 稀疏矩阵快速转置 【问题描述】 稀疏矩阵的存储不宜用二维数组存储每个元素,那样的话会浪费很多的存储空间。所以可以使用一个一维数组存…...

人体三维重构论文集合:awesome 3d human reconstruction
A curated list of related resources for 3d human reconstruction. Your contributions are welcome! Contents papers AIGCnerf or pifugeo fusionphoto3D human whole body3D human...

揭秘Redis持久化原理,探索fork与Copy-on-Write的魔法!
大家好,我是小米,今天我将和大家一起探索Redis持久化原理中的两个关键概念:fork和Copy-on-Write。这两个概念对于理解Redis的数据持久化机制至关重要。让我们一起来揭开这些技术的神秘面纱吧! Redis持久化简介 在开始之前&#…...

应届生如何提高职场竞争能力
摘要: 应届生面对竞争激烈的职场,需要不断提高自身的职业素养和竞争能力,才能在激烈的竞争中脱颖而出。本文从积极心态的培养、专业知识的优化、职业规划的制定、团队协作的加强和自我拓展的开展五个方面,提出了提高应届生职场竞争…...
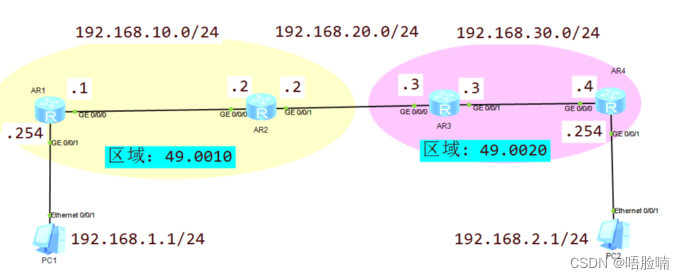
ISIS 实验
(1)拓扑图 2)需求: -实现PC1和PC2的通信 3)配置步骤: -配置接口IP地址 -开启ISIS---类似于在OSPF中创建进程 -配置NET地址---类似于在OSPF中创建区域,指定Router-id -在接口上启用ISIS--类似于在OSPFv2中用ne…...

国产系统:麒麟之人大金仓数据库部署
一、基本信息和资源 1.1 查看服务器信息 [root7PGxjKPL4 ~]# cat /etc/*release Kylin Linux Advanced Server release V10 (Sword) DISTRIB_IDKylin DISTRIB_RELEASEV10 DISTRIB_CODENAMEjuniper DISTRIB_DESCRIPTION"Kylin V10" DISTRIB_KYLIN_RELEASEV10 DISTRI…...
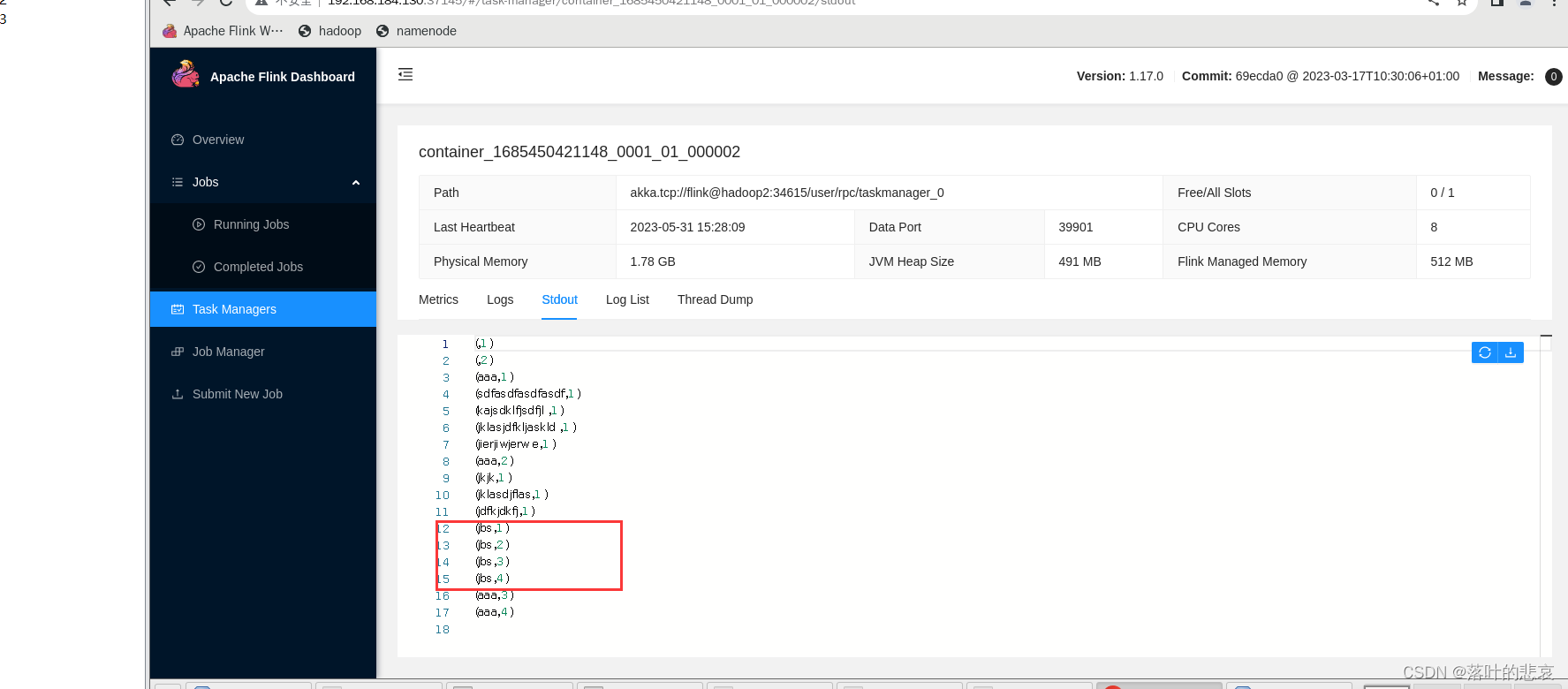
flink1.17.0 集成kafka,并且计算
前言 flink是实时计算的重要集成组件,这里演示如何集成,并且使用一个小例子。例子是kafka输入消息,用逗号隔开,统计每个相同单词出现的次数,这么一个功能。 一、kafka环境准备 1.1 启动kafka 这里我使用的kafka版本…...

【华为OD机试】数组组成的最小数字【2023 B卷|100分】
【华为OD机试】-真题 !!点这里!! 【华为OD机试】真题考点分类 !!点这里 !! 题目描述: 给定一个整型数组,请从该数组中选择3个元素组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述: 一行用半角逗号分割的字符串记录的整型数…...

Exponential Loss 中的关于indicator 函数的一个恒等式
− x y 2 I ( x ≠ y ) − 1 -xy2\mathbf{ I}(x \ne y)-1 −xy2I(xy)−1 其中 I \mathbf{ I} I 是 indicator 函数, 定义域 为True ,函数值为 1 反之为 0 x,y 都 可以取值 {-1,1} 证明过程见下表: xy左式右式-1-1-1-111-1-1-11111-111...
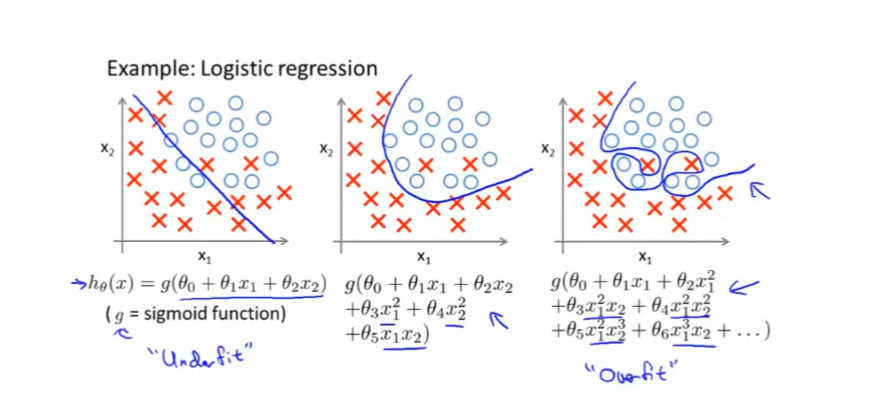
【机器学习】浅析过拟合
过度拟合 我们来想象如下一个场景:我们准备了10000张西瓜的照片让算法训练识别西瓜图像,但是这 10000张西瓜的图片都是有瓜梗的,算法在拟合西瓜的特征的时候,将西瓜带瓜梗当作了一个一般性的特征。此时出现一张没有瓜梗的西瓜照片…...
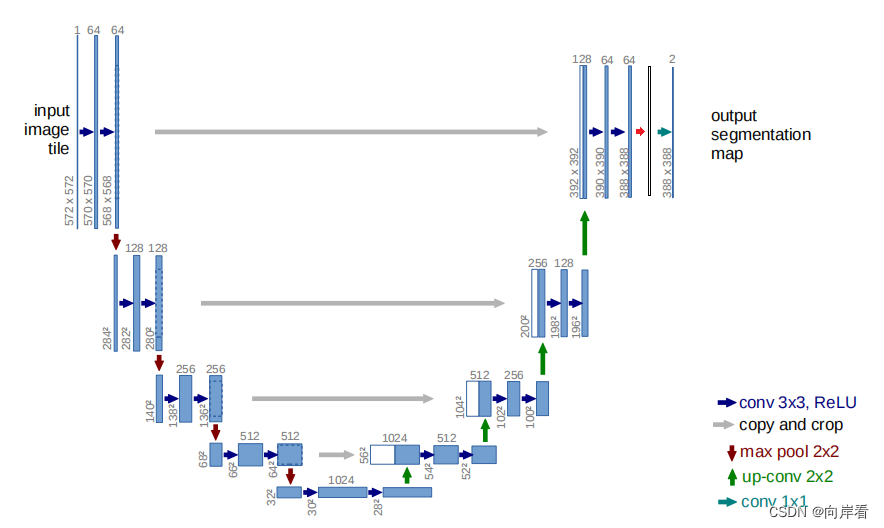
尝试在UNet的不同位置添加SE模块
目录 (1)se-unet01(在卷积后,下采样前,添加SE模块) (2)se-unet02(在卷积后,上采样前,添加SE模块) (3)se-un…...
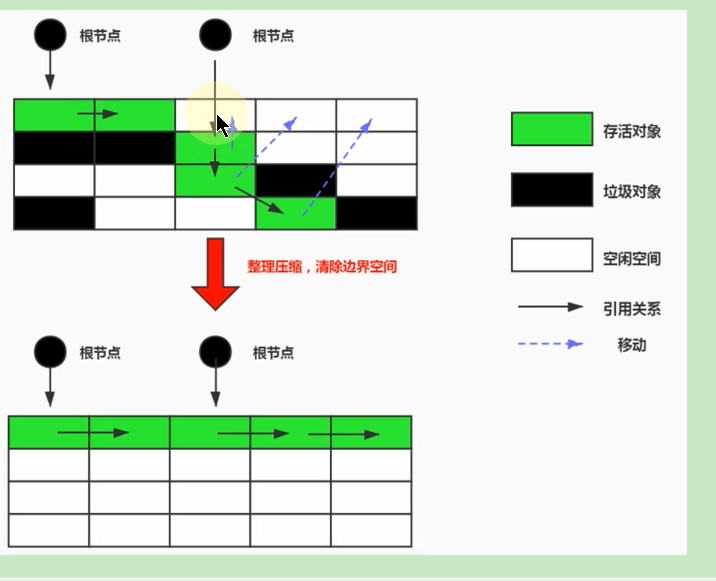
JVM垃圾回收篇之相关概念和算法
垃圾回收相关概念 什么是垃圾 垃圾就是指在运行程序中没有任何指针指向的对象,这个对象就是需要被回收掉的垃圾,如果不及时进行清理,越积越多就会导致内存溢出. 为什么需要GC 不进行回收,早晚会导致内存溢出,Java自动管理垃圾回收,不需要开发人员手动干预,这就有可能导致开…...
(学习日记)2023.04.27
写在前面: 由于时间的不足与学习的碎片化,写博客变得有些奢侈。 但是对于记录学习(忘了以后能快速复习)的渴望一天天变得强烈。 既然如此 不如以天为单位,以时间为顺序,仅仅将博客当做一个知识学习的目录&a…...

亚马逊CPC广告每日该怎么调整?
01 CPC广告需要每日调整吗? 其实,亚马逊广告是不建议每天都做过多调整的。 为什么呢?调整太频繁了,看不到每天调整的结果是不是? 什么时候需要调整呢? 就是广告指标,比如说曝光、点击、转化率情…...
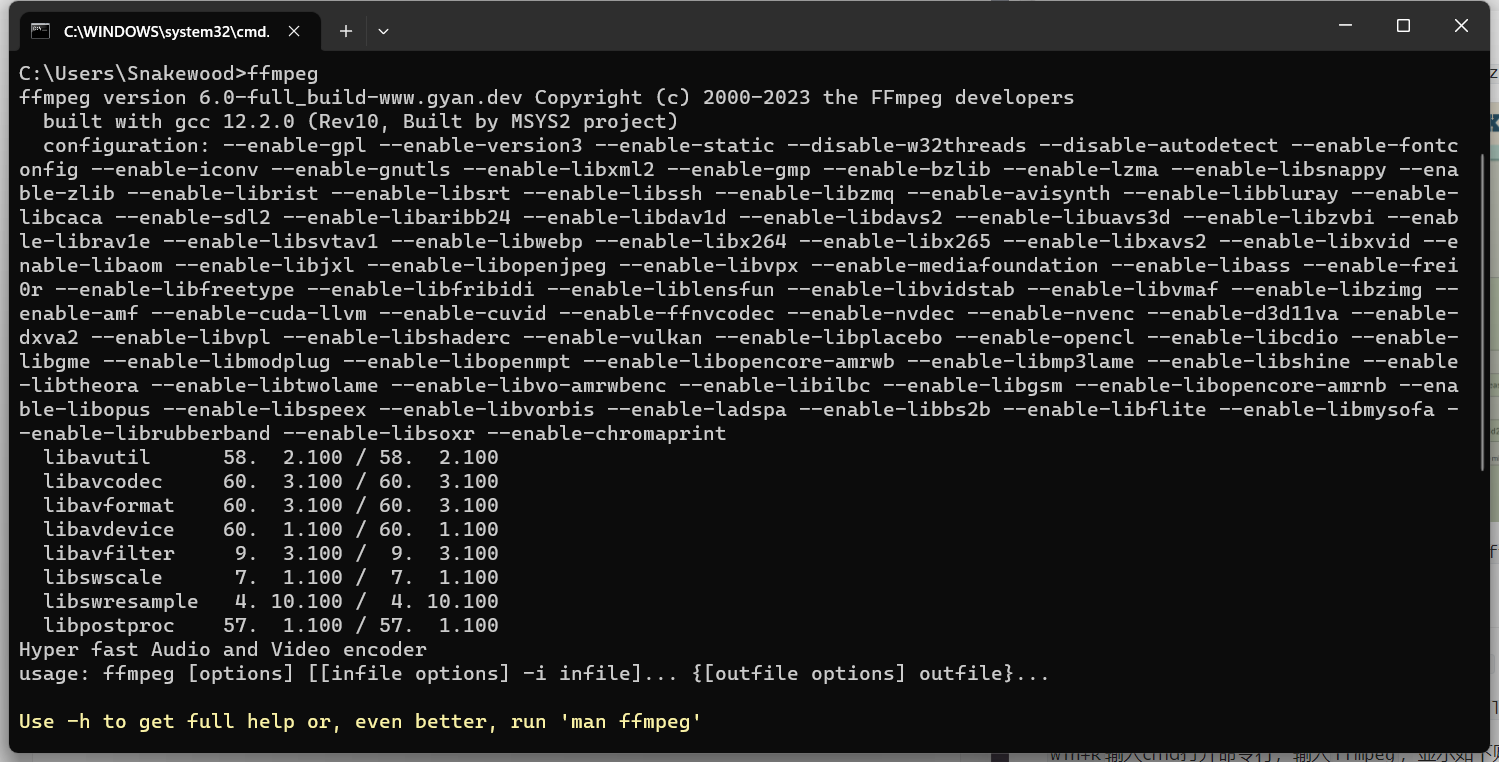
ffmpeg下载及ffmpy3安装使用
ffmpeg下载及ffmpy3安装使用 1.下载ffmpeg 进入网址:https://www.gyan.dev/ffmpeg/builds/ 在release builds中下载ffmpeg-release-full.7z 下载好后解压到自己想存放的目录,例如:D:\Tool\ffmpeg-6.0-full_build 2.配置环境变量 右键此电…...

设计模式之~原型模式
定义:用原型实例指导创建对象的种类,并且通过拷贝这些原型创建新的对象。原型模式其实就是从一个对象再创建另外一个可定制的对象,而且不需知道任何创建的细节。 优点: 一般在初始化的信息不发生变化的情况下,克隆是最…...

多传感器融合SLAM --- 8.LIO-SAM基础知识解读
目录 1 惯性测量单元简介及预积分 1.1 IMU 器件介绍及选型建议 1.2 IMU状态传递方程...

多模态大模型时代下的文档图像智能分析与处理
多模态大模型时代下的文档图像智能分析与处理 0. 前言1. 人工智能发展历程1.1 传统机器学习1.2 深度学习1.3 多模态大模型时代 2. CCIG 文档图像智能分析与处理论坛2.1 文档图像智能分析与处理的重要性和挑战2.2 文档图像智能分析与处理高峰论坛2.3 走进合合信息 3. 文档图像智…...
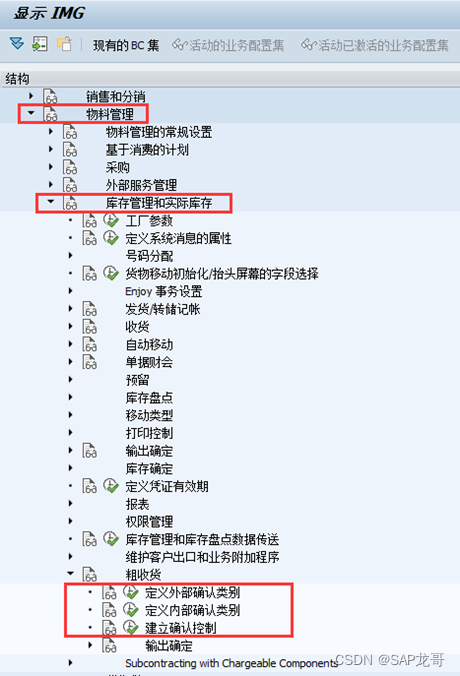
SAP-MM-内向外向交货单
1、内向&外向交货单概念 外向交货(outbound delivery)是用在客户与企业之间的交货单,而内向交货(inbound delivery)则是用在供应商与企业之间的交货单;换言之,外向交货多用于SD 模块&#…...

Mysql - date、datetime、timestamp 的区别
date、datetime 的区别 顾名思义,date 日期,datetime 日期时间,所以 date 是 datetime 的日期部分MySQL 以 格式检索和显示 datetime 值 YYYY-MM-DD hh:mm:ss datetime 支持的日期时间范围 1000-01-01 00:00:00 ~ 9999-12-31 23:59:59 d…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
