平面最近点对(分治算法)
文章目录
- 平面最近点对(分治算法)
- Solution
- 流程
- 完整模板代码
平面最近点对(分治算法)
文章首发于我的个人博客:欢迎大佬们来逛逛
平面最近点对(加强版) - 洛谷
给你一些点,求两点之间距离最小的两个点之间的最短距离。
分治算法是解决这类问题的关键。
Solution
首先将所有的点按照 x x x 为第一关键字, y y y 为第二关键字进行排序。
排序后如下:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pGAMATS2-1685532860870)(%E5%B9%B3%E9%9D%A2%E6%9C%80%E8%BF%91%E7%82%B9%E5%AF%B9%EF%BC%88%E5%88%86%E6%B2%BB%E7%AE%97%E6%B3%95%EF%BC%89%204c3ad0a0ba5c4743aed687f933a3e85a/Untitled.png)]
我们可以将所有的点分治:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7vB6twgs-1685532860871)(%E5%B9%B3%E9%9D%A2%E6%9C%80%E8%BF%91%E7%82%B9%E5%AF%B9%EF%BC%88%E5%88%86%E6%B2%BB%E7%AE%97%E6%B3%95%EF%BC%89%204c3ad0a0ba5c4743aed687f933a3e85a/Untitled%201.png)]
在这些点中我们用一条分割线来隔开,如果我们一直分割,则到最后 l + 1 = r l+1=r l+1=r 的时候,就表明划分到了最后的两个点,因此直接计算两个点之间的**距离;**如果最后只有一个点,即 l = r l=r l=r ,则我们规定此距离为无穷大。
因此我们得到两个点之间距离之后再回溯,寻找相对于这两个点有没有更优的点对出现,则更新,继续回溯。最后结束的时候,我们一定可以得到所有点的距离最短的距离。
树型图表示如下:
- 首先递归到 [ 1 , 2 ] [1,2] [1,2] 发现此时只有 p 1 和 p 2 p1 和p2 p1和p2 两个点,因此我们计算他们的最短距离,假设为 3
- 接着进入 [ 3 , 3 ] [3,3] [3,3] 此时只有一个点,因此规定距离为无穷大
- 然后我们回溯到 [ 1 , 3 ] [1,3] [1,3] ,取两个孩子节点的最小值,为3;但是此时并没有结束,我们获得的 3 只是分割线两侧分别计算的最优解,我们此时还需要得到去除分割线之后的所有点的之间的最短距离,更新为 p 1 和 p 3 p1 和 p3 p1和p3 之间的距离,为 2.
- 然后递归到 [ 4 , 5 ] [4,5] [4,5] 区间,得到 p 4 和 p 5 p4 和 p5 p4和p5 之间距离为 2.5。
- 然后回溯到 根节点 [ 1 , 5 ] [1,5] [1,5] ,得到分割线两侧的点之间的最优解,为2;接着计算去除分割线之后的两点之间的最优解,得到 1.2 ,为 p 3 和 p 4 p3 和 p4 p3和p4 之间的距离
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QEeXFBNB-1685532860871)(%E5%B9%B3%E9%9D%A2%E6%9C%80%E8%BF%91%E7%82%B9%E5%AF%B9%EF%BC%88%E5%88%86%E6%B2%BB%E7%AE%97%E6%B3%95%EF%BC%89%204c3ad0a0ba5c4743aed687f933a3e85a/Untitled%202.png)]
如何计算去除分割线之后的区间的两点的最短距离?
我们称之为 跨中线处理
- 首先由目标区间 [ l , r ] [l,r] [l,r] 得到所有 x x x 的差值小于 d d d 的点集合。
- 将这些点按照 y y y 值排序
- 最后直接两两之间暴力枚举 y y y 值的差值小于 d d d 的点对距离
流程
因此我们很轻松的得到分治求平面最近点对的流程:
- 首先将所有的点按照 x x x 和 y y y 为第一第二关键字排序。
- 然后递归分治所有的点,递归到终点时计算点的距离,回溯返回局部最优解。
- 然后计算全局最优解,即跨中线处理。
时间复杂度: O ( n l o g 2 n ) O(nlog^2n) O(nlog2n)
使用归并排序会降低为 O ( n l o g n ) O(nlogn) O(nlogn)
完整模板代码
#include<bits/stdc++.h>
#if 0#define int long long
#endifconst int N=200010;
int n;
struct point{double x,y;
}A[N],B[N],T[N];
double get_dis(const point& a,const point& b){return std::sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
double solve(int l,int r){//分治if (l==r){ //只有一个点return 1e9;}if (l+1==r){ //有两个点则算距离return get_dis(A[l],A[r]);}int mid=l+r>>1;double d=std::min(solve(l,mid),solve(mid+1,r)); //跨中线处理int k=0;for (int i=l;i<=r;i++){if (fabs(A[i].x-A[mid].x)<d){B[++k]=A[i];}}//按照y值排序std::sort(B+1,B+1+k,[&](const point& a,const point& b){return a.y<b.y;});for (int i=1;i<k;i++){//枚举两个点进行距离的更新for (int j=i+1;j<=k && B[j].y-B[i].y<d;j++){d=std::min(d,get_dis(B[i],B[j]));}}return d;
}
signed main(){std::cin>>n;for (int i=1;i<=n;i++){std::cin>>A[i].x>>A[i].y;}//1. 按照x为第一关键字,y为第二关键字排序std::sort(A+1,A+1+n,[&](const point& a,const point& b){if (a.x==b.x) return a.y<b.y;return a.x<b.x;});printf("%.4lf\n",solve(1,n));return 0;
}
相关文章:
)
平面最近点对(分治算法)
文章目录 平面最近点对(分治算法)Solution流程完整模板代码 平面最近点对(分治算法) 文章首发于我的个人博客:欢迎大佬们来逛逛 平面最近点对(加强版) - 洛谷 给你一些点,求两点之…...

【基于前后端分离的博客系统】Servlet版本
🎉🎉🎉点进来你就是我的人了博主主页:🙈🙈🙈戳一戳,欢迎大佬指点! 欢迎志同道合的朋友一起加油喔🤺🤺🤺 目录 一. 项目简介 1. 项目背景 2. 项目用到的技…...

在线Excel绝配:SpreadJS 16.1.1+GcExcel 6.1.1 Crack
前端:SpreadJS 16.1.1 后端: GcExcel 6.1.1 全能 SpreadJS 16.1.1此版本的产品中包含以下功能和增强功能。 添加了各种输入掩码样式选项。 添加了在保护工作表时设置密码以及在取消保护时验证密码的支持。 增强了组合图以将其显示为仪表图。 添加了…...

一个轻量的登录鉴权工具Sa-Token 集成SpringBoot简要步骤
Sa-Token 集成SpringBoot简要步骤 1.1 简单介绍 Sa-Token是一个轻量级Java权限认证框架。 主要解决的问题如下: 登录认证 权限认证 单点登录 OAuth2.0 分布式Session会话 微服务网关鉴权等一系列权限相关问题。 1.2 登录认证 设计思路 对于一些登录之后…...
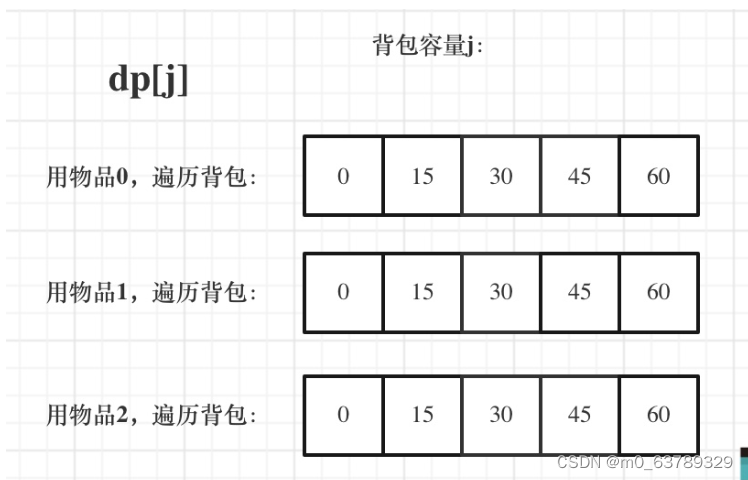
day 44 完全背包:518. 零钱兑换 II;377. 组合总和 Ⅳ
完全背包:物品可以使用多次 完全背包1. 与01背包区别 518. 零钱兑换 II1. dp数组以及下标名义2. 递归公式3. dp数组如何初始化4. 遍历顺序:不能颠倒两个for循环顺序5. 代码 377. 组合总和 Ⅳ:与零钱兑换类似,但是是求组合数1. dp数组以及下标名义2. 递归…...
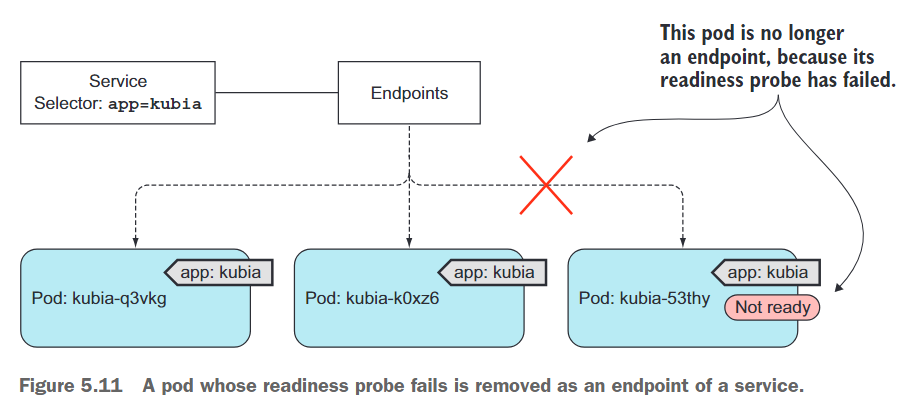
K8s in Action 阅读笔记——【5】Services: enabling clients to discover and talk to pods
K8s in Action 阅读笔记——【5】Services: enabling clients to discover and talk to pods 你已了解Pod以及如何通过ReplicaSets等资源部署它们以确保持续运行。虽然某些Pod可以独立完成工作,但现今许多应用程序需要响应外部请求。例如,在微服务的情况…...

牛客网DAY2(编程题)
圣诞节来啦!请用CSS给你的朋友们制作一颗圣诞树吧~这颗圣诞树描述起来是这样的: 1. "topbranch"是圣诞树的上枝叶,该上枝叶仅通过边框属性、左浮动、左外边距即可实现。边框的属性依次是:宽度为100px、是直线、颜色为gr…...
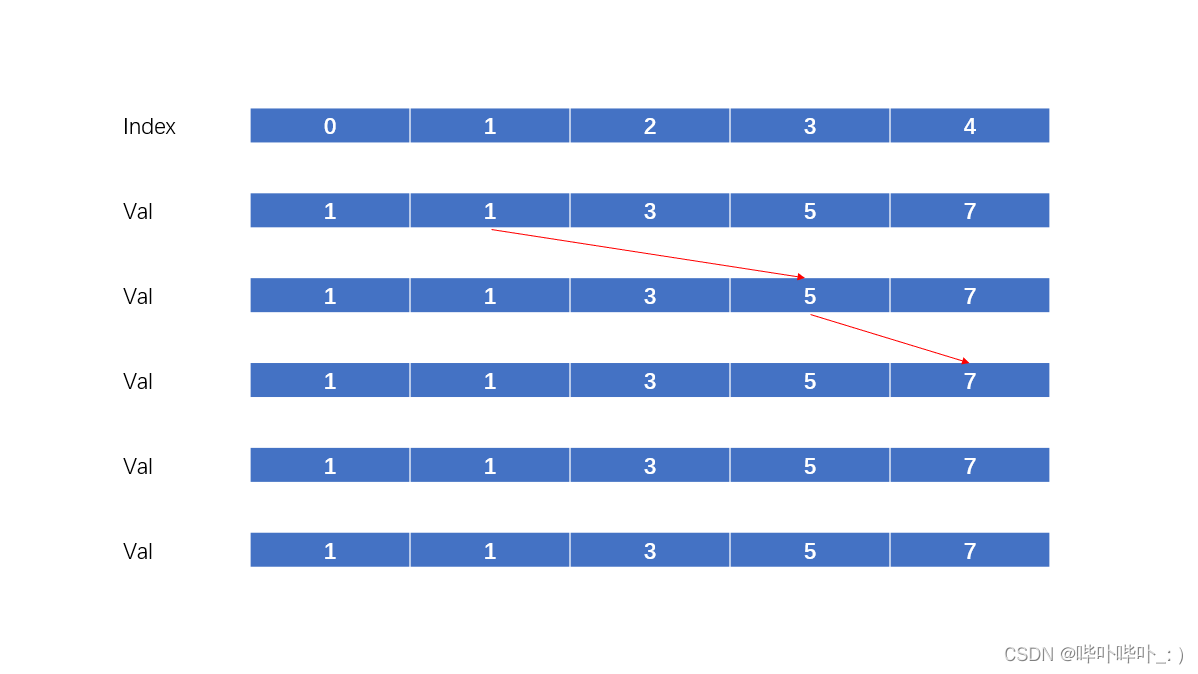
Java经典笔试题—day14
Java经典笔试题—day14 🔎选择题🔎编程题🍭计算日期到天数转换🍭幸运的袋子 🔎结尾 🔎选择题 (1)定义学生、教师和课程的关系模式 S (S#,Sn,Sd,Dc,SA )(其属性分别为学号、姓名、所…...

一个帮助写autoprefixer配置的网站
前端需要用到postcss的工具,用到一个插件叫autoprefixer,这个插件能够给css属性加上前缀,进行一些兼容的工作。 如何安装之类的问题在csdn上搜一下都能找到(注意,vite是包含postcss的,不用在项目中安装pos…...
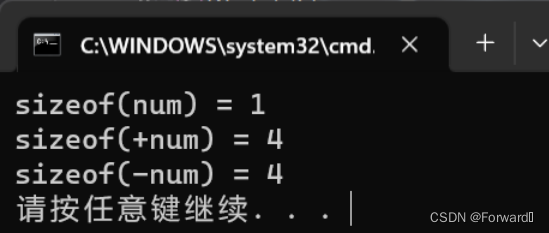
C语言中的类型转换
C语言中的类型转换 隐式类型转换 整型提升 概念: C语言的整型算术运算总是至少以缺省(默认)整型类型的精度来进行的为了获得这个精度,表达式中字符和短整型操作数在使用之前被转换为普通整型,这种转换成为整型提升 如…...
)
String底层详解(包括字符串常量池)
String a “abc”; ,说一下这个过程会创建什么,放在哪里? JVM会使用常量池来管理字符串直接量。在执行这句话时,JVM会先检查常量池中是否已经存有"abc",若没有则将"abc"存入常量池,否…...

C++ 里面lambda和函数指针的转换
问题说明 原始问题,代码如下会编译报错: using DecisionFn bool(*)();class Decide { public:Decide(DecisionFn dec) : _dec{dec} {} private:DecisionFn _dec; };int main() {int x 5;Decide greaterThanThree{ [x](){ return x > 3; } };retur…...

前端Rust开发WebAssembly与Swc插件快速入门
前言 现代前端对速度的追求已经进入二进制工具时代,Rust 开发成为每个人的必修课。 一般我们将常见的前端 Rust 开发分为以下几类,难度由上至下递增: 开发 wasm 。 开发 swc 插件。 开发代码处理工具。 我们将默认读者具备最简单的 Rus…...

【C++ 学习 ⑧】- STL 简介
目录 一、什么是 STL? 二、STL 的版本 三、STL 的 6 大组件和 13 个头文件 四、学习 STL 的 3 个境界 五、STL 的缺陷 参考资料: STL教程:C STL快速入门(非常详细) (biancheng.net)。 C STL是什么,有…...
论文笔记--Deep contextualized word representations
论文笔记--Deep contextualized word representations 1. 文章简介2. 文章概括3 文章重点技术3.1 BiLM(Bidirectional Language Model)3.2 ELMo3.3 将ELMo用于NLP监督任务 4. 文章亮点5. 原文传送门 1. 文章简介 标题:Deep contextualized word representations作者…...

【MySQL高级篇笔记-性能分析工具的使用 (中) 】
此笔记为尚硅谷MySQL高级篇部分内容 目录 一、数据库服务器的优化步骤 二、查看系统性能参数 三、统计SQL的查询成本:last_query_cost 四、定位执行慢的 SQL:慢查询日志 1、开启慢查询日志参数 2、查看慢查询数目 3、慢查询日志分析工具…...

大学生数学建模题论文
大学生数学建模题论文篇1 浅论高中数学建模与教学设想 论文关键词:数学建模 数学 应用意识 数学建模教学 论文摘要:为增强学生应用数学的意识,切实培养学生解决实际问题的能力,分析了高中数学建模的必要性,并通过对高中…...

论文阅读 —— 滤波激光SLAM
文章目录 FAST-LIO2FAST-LIOIMUR2LIVER3LIVEEKFLINS退化摘要第一句 FAST-LIO2 摘要: 本文介绍了FAST-LIO2:一种快速、稳健、通用的激光雷达惯性里程计框架。 FAST-LIO2建立在高效紧耦合迭代卡尔曼滤波器的基础上,有两个关键的新颖之处&#…...

JavaScript键盘事件
目录 一、keydown:按下键盘上的任意键时触发。 二、keyup:释放键盘上的任意键时触发。 三、keypress:在按下并释放能够产生字符的键时触发(不包括功能键等)。 四、input:在文本输入框或可编辑元素的内容…...

opengl灯光基础:2.1 光照基础知识
光照: 光照以不同的方式影响着我们看到的世界,有时甚至是以很戏剧化的方式。当手电筒照射在物体上时,我们希望物体朝向光线的一侧看起来更亮。我们所居住的地球上的点,在中午朝向太阳时候被照得很亮,但随着地球的自转…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
