【算法竞赛进阶指南】141.周期 题解 KMP 最小循环节
题目描述
一个字符串的前缀是从第一个字符开始的连续若干个字符,例如 abaab 共有 5 5 5 个前缀,分别是 a,ab,aba,abaa,abaab。
我们希望知道一个 N N N 位字符串 S S S 的前缀是否具有循环节。
换言之,对于每一个从头开始的长度为 i i i( i > 1 i>1 i>1)的前缀,是否由重复出现的子串 A A A 组成,即 A A A … A AAA…A AAA…A ( A A A 重复出现 K K K 次, K > 1 K>1 K>1)。
如果存在,请找出最短的循环节对应的 K K K 值(也就是这个前缀串的所有可能重复节中,最大的 K K K 值)。
输入格式
输入包括多组测试数据,每组测试数据包括两行。
第一行输入字符串 S S S 的长度 N N N。
第二行输入字符串 S S S。
输入数据以只包括一个 0 0 0 的行作为结尾。
输出格式
对于每组测试数据,第一行输出 Test case # 和测试数据的编号。
接下来的每一行,输出具有循环节的前缀的长度 i i i 和其对应 K K K,中间用一个空格隔开。
前缀长度需要升序排列。
在每组测试数据的最后输出一个空行。
数据范围
2 ≤ N ≤ 1000000 2 \le N \le 1000000 2≤N≤1000000
输入样例:
3
aaa
4
abcd
12
aabaabaabaab
0
输出样例:
Test case #1
2 2
3 3Test case #2Test case #3
2 2
6 2
9 3
12 4
题意重述
编写一个程序,对于每一个前缀子串 s i s_i si,找出它的最短循环节的重复次数。 s i s_i si 的最短循环节是指连续组合能恰好构成 s i s_i si 的最短的子串。例如,对于字符串 “aabaabaa”,“aab” 不是其最短循环节,因为它无法恰好构成原串。
注意,在以下叙述中,下标从1开始。
算法
通过KMP算法可以求得next数组,对于每一个前缀子串 s i s_i si,其最短循环节的长度就是 i − next [ s i ] i - \text{next}[s_i] i−next[si]。
为什么呢?
首先看图,上下两条线表示同一个字符串,重合的部分表示KMP匹配(前后缀相等的最大长度)。
上面的1就是下面的1(完全相同的部分),而下面的1等于上面的2(前后缀匹配),上面的2等于下面的2,而下面的2等于上面的3…
所以上面的1,2,3,4,5和下面的1,2,3,4,5完全相同。
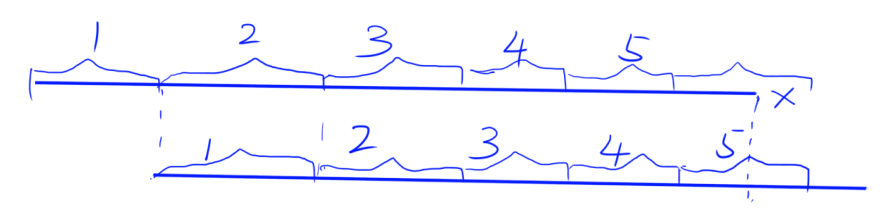
在不严格要求“恰好”构成时,每一小段都可以视作原串的循环节。然后,我们可以证明,这样的小段就是原串的最短循环节。
那么,如何证明呢?
反证: 假设该小段字符串T不是最短循环节,则原串中必然存在T’作为最短循环节。那么对于T’,可以按照上图的方式,将上下两串划分为一个个由T’组成的部分。
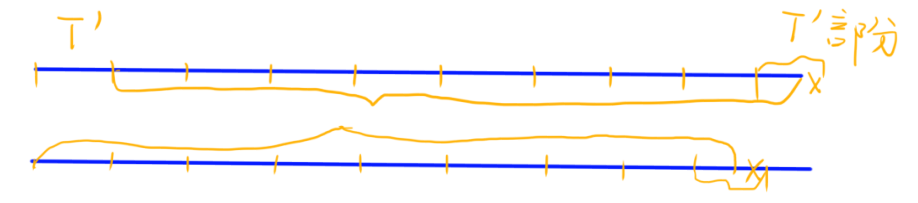
此时矛盾出现:如果可以用更小的T’划分,则根据图示,原串的KMP匹配长度就是 n − len ( T ′ ) n - \text{len}(T') n−len(T′)。这个长度 n − len ( T ′ ) n - \text{len}(T') n−len(T′) 超过了 n − len ( T ) n - \text{len}(T) n−len(T),而 n − len ( T ) n - \text{len}(T) n−len(T) 是原串的最大前后缀匹配长度。所以假设是错误的,也就是说,T确实是最短循环节。
当不严格要求“恰好”构成时, n − len ( T ) = n − next [ n ] n - \text{len}(T) = n - \text{next}[n] n−len(T)=n−next[n] 就是最短循环节的长度。对于每一个前缀子串 s i s_i si,其最短循环节的长度就是 i − next [ i ] i - \text{next}[i] i−next[i]。那么,当我们严格要求恰好构成时,又会是怎样呢?
我们可以证明一个引理,一个字符串的任何循环节(除最短循环节外)都是最短循环节的倍数。也就是说,不存在其他可能的模式使得原串能够恰好由其循环构成。因此,如果原串长度能被 l e n ( T ) len(T) len(T) 整除,则存在最短循环节且为 s [ 1 ∼ l e n ( T ) ] s[1\sim len(T)] s[1∼len(T)],如果不能被整除,则不存在(按题目的要求,不能“恰好”构成就是为不存在)。
引理证明:
反证: 假设原串存在一个子串T’,它不是最短循环节,也不是最短循环节的循环构成(倍数),但是可以循环构成原串。(有点绕)
这就意味着 l e n ( T ′ ) > l e n ( T ) len(T') > len(T) len(T′)>len(T),且 l e n ( T ′ ) len(T') len(T′) 不是 l e n ( T ) len(T) len(T) 的倍数。根据循环节的定义,T 和 T’ 都可以构成原串。即原串可以写为 T T . . . T A TT...TA TT...TA(T出现 m 次)或 T ′ T ′ . . . T ′ B T'T'...T'B T′T′...T′B(T’出现 n 次)。这里的 A 和 B 可能是空串,或者长度不足一个 T 或 T’ 的部分。满足 m × l e n ( T ) = n × l e n ( T ′ ) m \times len(T) = n \times len(T') m×len(T)=n×len(T′)。
于是我们可以找到一个更小的循环节,其长度为d,因为
s j = s j + l e n ( T ) = s j + 2 l e n ( T ) = ⋯ = s j + x l e n ( T ) = s j + x l e n ( T ) − l e n ( T ′ ) = s j + x l e n ( T ) − 2 l e n ( T ′ ) = ⋯ = s j + x l e n ( T ) − y l e n ( T ′ ) = s j + d s_j=s_{j+len(T)}=s_{j+2len(T)}= \cdots =s_{j+xlen(T)}=s_{j+xlen(T)-len(T')}=s_{j+xlen(T)-2len(T')}=\cdots =s_{j+xlen(T)-ylen(T')}=s_{j+d} sj=sj+len(T)=sj+2len(T)=⋯=sj+xlen(T)=sj+xlen(T)−len(T′)=sj+xlen(T)−2len(T′)=⋯=sj+xlen(T)−ylen(T′)=sj+d
此处的 j j j 可以从几乎任意位置开始,只要字符串的长度足够长以支持所描述的周期 (如果不支持,那么表示从j开始的后续部分无法使用T’进行重复构成,这样的情况则不需要讨论。)。
但这与T是最短循环节的假设产生矛盾,假设不成立。故不存在一种循环节使得它既不是最短循环节,也不是最短循环节的倍数。
看明白了,请给我点赞,谢谢(*^▽^*)。
时间复杂度 O ( n ) \mathcal{O}(n) O(n)
KMP+线性扫描, O ( n ) \mathcal{O}(n) O(n)。
C++ 代码
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e6 + 10;
char s[N]; int ne[N];int main(){int T = 1;int n;while(scanf("%d", &n), n){printf("Test case #%d\n", T ++);scanf("%s", s + 1);for(int i = 2, j = 0; i <= n; ++ i){while(j && s[i] != s[j + 1]) j = ne[j];if(s[i] == s[j + 1]) j ++;ne[i] = j;}for(int i = 1; i <= n; ++ i){int t = i - ne[i];if(i > t && i % t == 0){ // i>t保证循环节至少出现2次printf("%d %d\n", i, i / t);}}puts("");}
}相关文章:

【算法竞赛进阶指南】141.周期 题解 KMP 最小循环节
题目描述 一个字符串的前缀是从第一个字符开始的连续若干个字符,例如 abaab 共有 5 5 5 个前缀,分别是 a,ab,aba,abaa,abaab。 我们希望知道一个 N N N 位字符串 S S S 的前缀是否具有循环节。 换言之…...

【Springboot 入门培训 】#19 Spring Boot 组件扫描与bean生命周期
目录 1 什么是组件扫描2 何时使用组件扫描3 扫描整个包basePackages与 includeFilters4 Spring boot 的 Bean 生命周期4.1 生命周期4.2 Bean 生命周期4.3 周期各个阶段 首先,我想先为你介绍一下“Spring”,这是一个开放源代码的设计模式解决方案和轻量级…...

Linux printf 函数输出问题
printf 函数并不会直接将数据输出到屏幕,而是先放到缓冲区中,只有一下三种情况满足,才会输出到屏幕。 1) 缓冲区满 2) 强制刷新缓冲区 fflush 3) 程序结束时 1 #include<stdio.h>2 #include<st…...
皮卡丘Unsafe Fileupload
1.不安全的文件上传漏洞概述 文件上传功能在web应用系统很常见,比如很多网站注册的时候需要上传头像、上传附件等等。当用户点击上传按钮后,后台会对上传的文件进行判断 比如是否是指定的类型、后缀名、大小等等,然后将其按照设计的格式进行…...
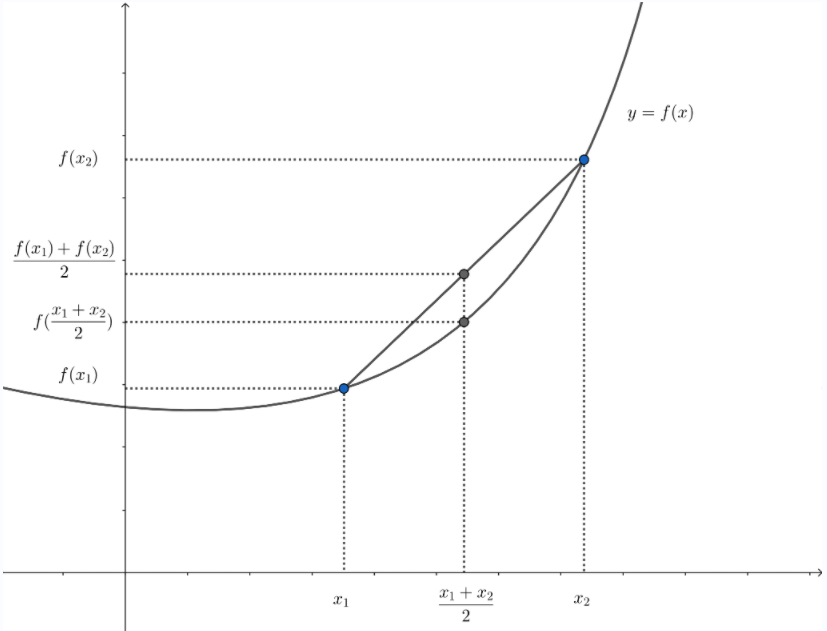
最优化简明版(上)
引言 本文简单地介绍一些凸优化(Convex Optimization)的基础知识,可能不会有很多证明推导,目的是能快速应用到机器学习问题上。 凸集 直线与线段 设 x 1 ≠ x 2 x_1 \neq x_2 x1x2为 R n \Bbb R^n Rn空间中的两个点,那么具有下列形…...

MySQL的一些介绍
1. SQL的select语句完整的执行顺序 SQL Select语句完整的执行顺序: 1、from子句组装来自不同数据源的数据; 2、where子句基于指定的条件对记录行进行筛选; 3、group by子句将数据划分为多个分组; 4、使用聚集函数进行计算&am…...

unity发布webGL后无法预览解决
众所周知,unity发布成webgl后是无法直接预览的。因为一般来说浏览器默认都是禁止webgl运行的。 直接说我最后的解决方法:去vscode里下载一个live server ,安装好。 下载vscode地址Visual Studio Code - Code Editing. Redefined 期间试过几种方法都不管…...
Flume和Kafka的组合使用
一.安装Kafka 1.1下载安装包 通过百度网盘分享的文件:复制链接打开「百度网盘APP 即可获取」 链接:https://pan.baidu.com/s/1vC6Di3Pml6k1KMbnK0OE1Q?pwdhuan 提取码:huan 也可以访问官网,下载kafka2.4.0的安装文件 1.2解…...
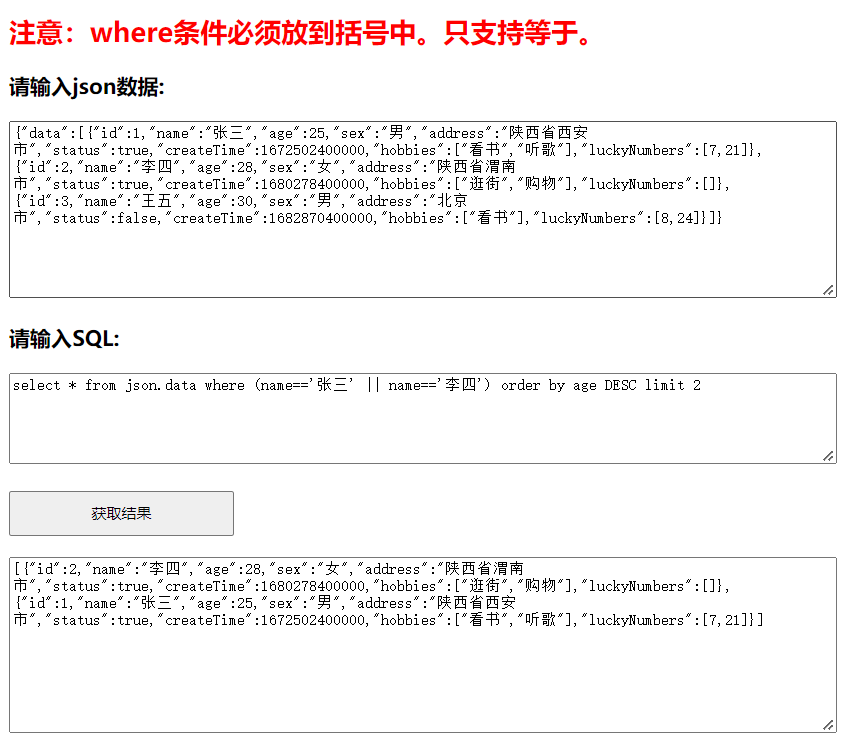
JSONSQL:使用SQL过滤JSON类型数据(支持多种数据库常用查询、统计、平均值、最大值、最小值、求和语法)...
1. 简介 在开发中,经常需要根据条件过滤大批量的JSON类型数据。如果仅需要过滤这一种类型,将JSON转为List后过滤即可;如果相同的条件既想过滤数据库表中的数据、也想过滤内存中JSON数据,甚至想过滤Elasticsearch中的数据ÿ…...
Linux输入输出重定向
目录 Linux输入输出重定向 Linux中的默认设备 输入输出重定向定义 输入输出重定向操作符 实用形式 标准输入、标准输出、标准错误 输出重定向案例 案例1 --- 输出重定向(覆盖) 案例2 --- 输出重定向(追加) 案例3 --- 错误…...
使用kettle进行数据统计
1.使用kettle设计一个能生成100个取值范围为0到100随机整数的转换。 为了完成该转换,需要使用生成记录控件、生成随机数控件、计算器控件及字段选择控件。控件布局如下图所示 生成记录控件可以在限制框内指定生成记录的个数,具体配置如图所示 生成随机数…...

线程的取消和清理
一、线程的取消 意义:随时杀掉一个线程 int pthread_cancel(pthread_t thread); 注意:线程的取消要有取消点才可以,不是说取消就取消,线程的取消点主要是阻塞的系统调用 二、运行段错误调试 可以使用gdb调试 使用gdb 运行代…...

day8 -- 全文本搜索
brief InnoDB存储引擎从MySQL 5.6开始支持全文本搜索。具体来说,MySQL使用InnoDB存储引擎的全文本搜索功能称为InnoDB全文本搜索(InnoDB Full-Text Search)。InnoDB全文本搜索支持标准的全文本搜索查询语法和多语言分词器,因此可…...

C语言:if-else语句
嗨,今天咱们讲讲C语言控制语句里的条件选择,主要总结下if else语句。 咱们生活里经常会有这样的场景,明天该怎么穿呢,得考虑下具体的天气。如果是晴天,温度还不错,可以穿T恤;如果是阴天…...

C语言---函数
1、函数是什么 学习库函数网站: https://cplusplus.com/reference/http://en.cppreference.comhttp://zh.cppreference.com 我们参考文档,学习几个库函数 2、库函数 3、自定义函数 自定义函数和库函数一样,有函数名,返回值类…...
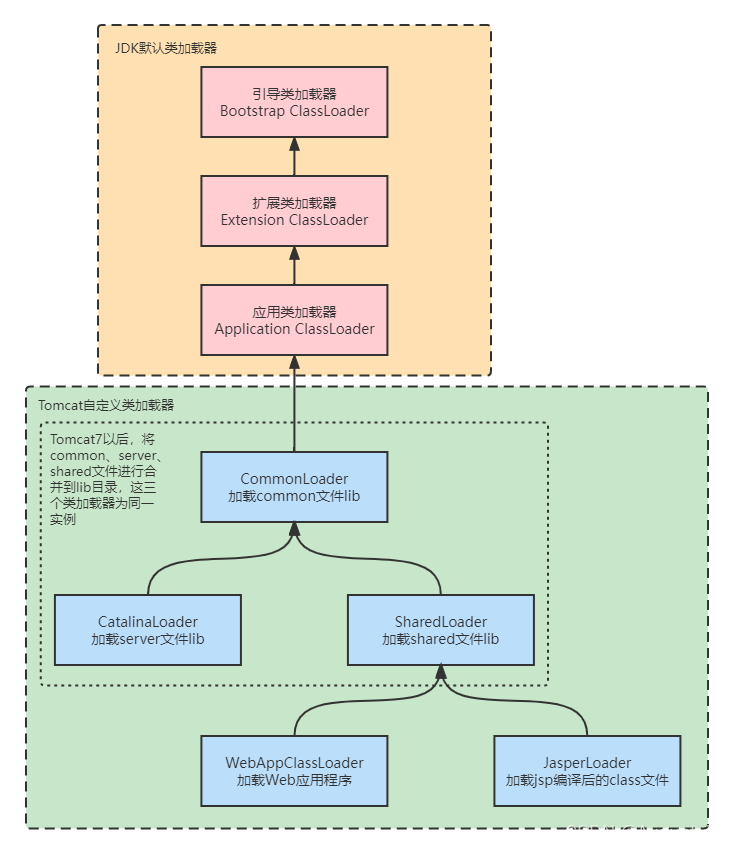
【JVM】什么是双亲委派机制?
一、为什么会有这种机制? 类加载器将.class类加载到内存中时,为了避免重复加载(确保Class对象的唯一性)以及JVM的安全性,需要使用某一种方式来实现只加载一次,加载过就不能被修改或再次加载。 二、什么是双…...

Vulkan Tutorial 7 纹理贴图
目录 23 图像 图片库 暂存缓冲区 纹理图像 布局转换 将缓冲区复制到图像上 准备纹理图像 传输屏障掩码 清除 24 图像视图和采样器 纹理图像视图 采样器 Anisotropy 设备特征 25 组合图像采样器 更新描述符 纹理坐标系 着色器 23 图像 添加纹理将涉及以下步骤&am…...

LinkedBlockingQueue阻塞队列
➢ LinkedBlockingQueue阻塞队列 LinkedBlockingQueue类图 LinkedBlockingQueue 中也有两个 Node 分别用来存放首尾节点,并且里面有个初始值为 0 的原子变量 count 用来记录队列元素个数,另外里面有两个ReentrantLock的独占锁,分别用来控制…...

面试-Redis 常见问题,后续面试遇到新的在补充
面试-Redis 1.谈谈Redis 缓存穿透,击穿,雪崩及如何避免 缓存穿透:是指大量访问请求在访问一个不存在的key,由于key 不存在,就会去查询数据库,数据库中也不存在该数据,无法将数据存储到redis 中…...

2023年上半年数据库系统工程师上午真题及答案解析
1.计算机中, 系统总线用于( )连接。 A.接口和外设 B.运算器、控制器和寄存器 C.主存及外设部件 D.DMA控制器和中断控制器 2.在由高速缓存、主存和硬盘构成的三级存储体系中,CPU执行指令时需要读取数据,那么DMA控制器和中断CPU发出的数据地…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...

联邦学习带宽资源分配
带宽资源分配是指在网络中如何合理分配有限的带宽资源,以满足各个通信任务和用户的需求,尤其是在多用户共享带宽的情况下,如何确保各个设备或用户的通信需求得到高效且公平的满足。带宽是网络中的一个重要资源,通常指的是单位时间…...

AWSLambda之设置时区
目标 希望Lambda运行的时区是东八区。 解决 只需要设置lambda的环境变量TZ为东八区时区即可,即Asia/Shanghai。 参考 使用 Lambda 环境变量...

Unity VR/MR开发-开发环境准备
视频讲解链接: 【XR马斯维】UnityVR/MR开发环境准备【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...
