最优化简明版(上)
引言
本文简单地介绍一些凸优化(Convex Optimization)的基础知识,可能不会有很多证明推导,目的是能快速应用到机器学习问题上。
凸集
直线与线段
设 x 1 ≠ x 2 x_1 \neq x_2 x1=x2为 R n \Bbb R^n Rn空间中的两个点,那么具有下列形式的点
y = θ x 1 + ( 1 − θ ) x 2 , θ ∈ R y= \theta x_1 + (1-\theta)x_2,\, \theta \in \Bbb R y=θx1+(1−θ)x2,θ∈R
组成一条穿越 x 1 x_1 x1和 x 2 x_2 x2的直线。
如果参数 θ \theta θ的值在 0 0 0到 1 1 1之间变动,就构成了 x 1 x_1 x1和 x 2 x_2 x2之间的线段。
仿射集合
如果通过集合 C ⊆ R n C \subseteq \Bbb R^n C⊆Rn中任意两个不同点的直线仍然在集合 C C C中,那么称集合 C C C是仿射的。
可以扩展到多个点的情况,如果 θ 1 + ⋯ + θ k = 1 \theta_1+ \cdots + \theta_k=1 θ1+⋯+θk=1,我们称具有 θ 1 x 1 + ⋯ + θ k x k \theta_1 x_1 + \cdots + \theta_k x_k θ1x1+⋯+θkxk形式的点为 x 1 , ⋯ , x k x_1,\cdots, x_k x1,⋯,xk的仿射组合。
凸集
首先来了解下什么是凸集(Convex Set)。
集合 C C C被称为凸集,如果 C C C中任意两点间的线段仍然在 C C C中,即对于任意 x 1 , x 2 ∈ C x_1,x_2 \in C x1,x2∈C和满足 0 ≤ θ ≤ 1 0\leq \theta \leq 1 0≤θ≤1的 θ \theta θ都有
θ x 1 + ( 1 − θ ) x 2 ∈ C (1) \theta x_1 + (1-\theta)x_2 \in C \tag{1} θx1+(1−θ)x2∈C(1)
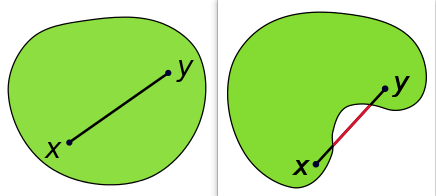
直观上来看,凸集的形状是饱满的,即没有凹进去的地方。
我们称
θ x 1 + ( 1 − θ ) x 2 (2) \theta x_1 + (1-\theta)x_2 \tag{2} θx1+(1−θ)x2(2)
为点 x 1 , x 2 x_1,x_2 x1,x2的凸组合,类似地,可以推广到多个点:
θ 1 x 1 + ⋯ + θ k x k (3) \theta_1 x_1 + \cdots + \theta_kx_k \tag{3} θ1x1+⋯+θkxk(3)
为点 x 1 , ⋯ , x k x_1,\cdots,x_k x1,⋯,xk的一个凸组合,其中 θ 1 + ⋯ + θ k = 1 \theta_1 + \cdots + \theta_k=1 θ1+⋯+θk=1且 θ i ≥ 0 , i = 1 , ⋯ , k \theta_i \geq 0, \, i=1,\cdots,k θi≥0,i=1,⋯,k。
一个集合是凸集也可以说集合包含其中所有点的凸组合。
我们称集合 C C C中所有点的凸组合的集合为其凸包,记作 conv C \text{conv} \,C convC。
多个凸集的交集也是凸集,这意味着如果每个不等式或等式约束条件定义的集合都是凸集,那么这些条件联合起来定义的集合仍然是凸集。
基于凸集的概念可以定义凸函数。
凸函数
函数 f : R n → R f : \Bbb R^n \rightarrow \Bbb R f:Rn→R是凸的,如果函数的定义域( dom f \text{dom}\, f domf)是凸集,且对于任意 x 1 , x 2 ∈ dom f x_1,x_2 \in \text{dom}\, f x1,x2∈domf和任意的 0 ≤ θ ≤ 1 0 \leq \theta \leq 1 0≤θ≤1,有
f ( θ x 1 + ( 1 − θ ) x 2 ) ≤ θ f ( x 1 ) + ( 1 − θ ) f ( x 2 ) (4) f(\theta x_1 + (1-\theta)x_2) \leq \theta f(x_1) + (1-\theta) f(x_2) \tag{4} f(θx1+(1−θ)x2)≤θf(x1)+(1−θ)f(x2)(4)
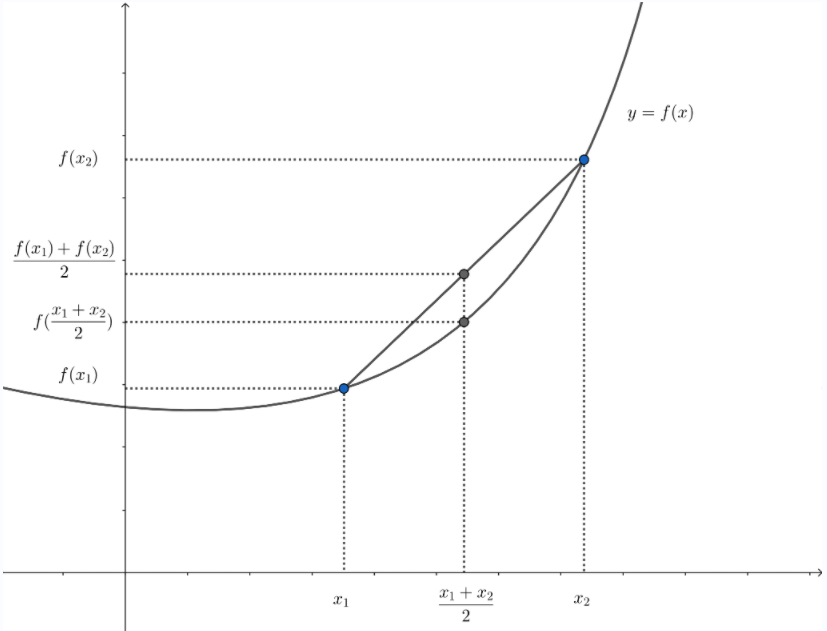
如图2(取 θ = 1 2 \theta=\frac{1}{2} θ=21),从几何意义上看,式 ( 4 ) (4) (4)的不等式成立意味着点 ( x 1 , f ( x 1 ) ) (x_1,f(x_1)) (x1,f(x1))和 ( x 2 , f ( x 2 ) ) (x_2,f(x_2)) (x2,f(x2))之间的线段,即从 x 1 x_1 x1到 x 2 x_2 x2的弦,在函数 f f f的图像上方。
反之,如果式 ( 4 ) (4) (4)中的函数为 ≥ \geq ≥,则称为凹函数。如果 f f f是凸函数,那么 − f -f −f就是凹函数。注意,还有很多函数是非凸也非凹的。
凸函数的一个很好的性质是,它只有一个局部极小值点,同时也是全局最小值点。
凸优化问题
优化问题
我们用
minimize f 0 ( x ) s.t. f i ( x ) ≤ 0 , i = 1 , … , m h i ( x ) = 0 , i = 1 , … , p (5) \begin{aligned} &\text{minimize}\quad &&f_0(x)\\ &\text{s.t.}\quad &&f_i(x) \leq 0,\quad i=1,\dots,m\\ &&&h_i(x) = 0,\quad i=1,\dots,p \end{aligned} \tag{5} minimizes.t.f0(x)fi(x)≤0,i=1,…,mhi(x)=0,i=1,…,p(5)
描述在所有满足 f i ( x ) ≤ 0 , i = 1 , ⋯ , m f_i(x) \leq 0,\, i=1,\cdots,m fi(x)≤0,i=1,⋯,m及 h i ( x ) = 0 , i = 1 , ⋯ , p h_i(x)=0,\,i=1,\cdots,p hi(x)=0,i=1,⋯,p的 x x x中寻找极小化 f 0 ( x ) f_0(x) f0(x)的 x x x的问题,即优化问题。
-
x ∈ R n x \in \Bbb R^n x∈Rn为优化变量;
-
函数 f 0 : R n → R f_0 : \Bbb R^n \rightarrow \Bbb R f0:Rn→R为目标函数;
-
不等式 f i ( x ) ≤ 0 f_i(x) \leq 0 fi(x)≤0称为不等式约束,相应的函数 f i : R n → R f_i: \Bbb R^n \rightarrow \Bbb R fi:Rn→R称为不等式约束函数;
-
方程组 h i ( x ) = 0 h_i(x) =0 hi(x)=0称为等式约束,相应的函数 h i : R n → R h_i: \Bbb R^n \rightarrow \Bbb R hi:Rn→R称为等式约束函数。
如果没有约束,即 m = p = 0 m=p=0 m=p=0,我们称问题 ( 5 ) (5) (5)为无约束问题。
对目标和所有约束函数有定义的点的集合
D = ⋂ i = 0 m dom f i ∩ ⋂ i = 1 p dom h i \mathcal D = \bigcap_{i=0}^m \text{dom}\, f_i \cap \bigcap_{i=1}^p \text{dom}\, h_i D=i=0⋂mdomfi∩i=1⋂pdomhi
称为优化问题 ( 5 ) (5) (5)的定义域。当点 x ∈ D x \in \cal D x∈D满足约束 f i ( x ) ≤ 0 , i = 1 , ⋯ , m f_i(x) \leq 0,\, i=1,\cdots,m fi(x)≤0,i=1,⋯,m和 h i ( x ) = 0 , i = 1 , ⋯ , p h_i(x)=0,\, i=1,\cdots, p hi(x)=0,i=1,⋯,p时, x x x是可行的。当问题 ( 5 ) (5) (5)至少有一个可行点时,我们称为可行的,否则称为不可行。所有可行点的集合称为可行集或约束集。
如果 x ∗ x^* x∗是可行的并且 f 0 ( x ∗ ) = p ∗ f_0(x^*)=p^* f0(x∗)=p∗最优值,我们称 x ∗ x^* x∗为最优点。如果问题存在最优解,我们称最优质是课的或可达的,称问题可解。
如果 x x x可行且 f i ( x ) = 0 f_i(x)=0 fi(x)=0,我们称约束 f i ( x ) ≤ 0 f_i(x)\leq 0 fi(x)≤0的第 i i i个不等式在 x x x处起作用。如果 f i ( x ) < 0 f_i(x) < 0 fi(x)<0,则约束 f i ( x ) ≤ 0 f_i(x) \leq 0 fi(x)≤0不起作用。我们称约束是冗余的,如果去掉它不改变可行集。
凸优化
凸优化问题是形如
minimize f 0 ( x ) s.t. f i ( x ) ≤ 0 , i = 1 , … , m a i T x = b i , i = 1 , ⋯ , p (6) \begin{aligned} &\text{minimize}\quad &&f_0(x)\\ &\text{s.t.}\quad &&f_i(x) \leq 0,\quad i=1,\dots,m\\ &&&a_i^Tx = b_i,\quad\, i=1,\cdots,p \end{aligned} \tag{6} minimizes.t.f0(x)fi(x)≤0,i=1,…,maiTx=bi,i=1,⋯,p(6)
的问题,其中 f 0 , ⋯ , f m f_0,\cdots,f_m f0,⋯,fm为凸函数,对比优化问题 ( 5 ) (5) (5),凸优化问题有三个附加的要求:
- 目标函数必须是凸的;
- 不等式约束函数必须是凸的;
- 等式约束函数 h i ( x ) = a i T − b i h_i(x) = a^T_i - b_i hi(x)=aiT−bi必须是仿射的;
立即可以看到一个重要的性质:凸优化问题的可行集是凸的。
带约束的优化问题
拉格朗日乘子法
拉格朗日乘子法(Lagrange Multiplier Method)用于求解带等式约束条件的函数极值(优化问题)。假设有如下极值问题
minimize f ( x ) s.t. h i ( x ) = 0 , i = 1 , … , p (7) \begin{aligned} &\text{minimize}\quad &&f(x)\\ &\text{s.t.}\quad &&h_i(x) = 0,\quad i=1,\dots,p\\ \end{aligned} \tag{7} minimizes.t.f(x)hi(x)=0,i=1,…,p(7)
拉格朗日乘子法构造如下拉格朗日乘子函数
L ( x , λ ) = f ( x ) + ∑ i = 1 p λ i h i ( x ) (8) L(x,\lambda) = f(x) + \sum_{i=1}^p \lambda_i h_i(x) \tag{8} L(x,λ)=f(x)+i=1∑pλihi(x)(8)
其中 λ \lambda λ为新引入的自变量,称为拉格朗日乘子((Lagrange Multiplier)。构造了该函数之后,去掉了对优化变量的等式约束。对拉格朗日乘子函数的所有自变量求偏导,并令其为 0 0 0。包括对 x x x求导、对 λ \lambda λ求导。得到下面的方程组:
∇ x f ( x ) + ∑ i = 1 p λ i ∇ x h i ( x ) = 0 h i ( x ) = 0 (9) \begin{aligned} \nabla_x f(x) + \sum_{i=1}^p \lambda_i \nabla_x h_i(x) &= 0 \\ h_i(x) &= 0 \end{aligned} \tag{9} ∇xf(x)+i=1∑pλi∇xhi(x)hi(x)=0=0(9)
求解该方程组即可得到函数的候选极值点。
拉格朗日对偶
对偶是求解最优化问题的一种手段,它将一个最优化问题转换为另一个更容易求解的问题,这两个问题是等价的。
对于如下带等式约束和不等式约束的优化问题:
minimize f ( x ) s.t. g i ( x ) ≤ 0 , i = 1 , … , m h i ( x ) = 0 , i = 1 , … , p (10) \begin{aligned} &\text{minimize}\quad &&f(x)\\ &\text{s.t.}\quad &&g_i(x) \leq 0,\quad i=1,\dots,m\\ &&&h_i(x) = 0,\quad i=1,\dots,p \end{aligned} \tag{10} minimizes.t.f(x)gi(x)≤0,i=1,…,mhi(x)=0,i=1,…,p(10)
仿照拉格朗日乘子法构造广义拉格朗日乘子函数
L ( x , λ , μ ) = f ( x ) + ∑ i = 1 m λ i g i ( x ) + ∑ i = 1 p μ i h i ( x ) (11) L(x,\lambda,\mu ) = f(x) + \sum_{i=1}^m \lambda_i g_i(x) + \sum_{i=1}^p \mu_i h_i(x) \tag{11} L(x,λ,μ)=f(x)+i=1∑mλigi(x)+i=1∑pμihi(x)(11)
称 λ \lambda λ和 μ \mu μ为拉格朗日乘子,特别要求 λ i ≥ 0 \lambda_i \geq 0 λi≥0。接下来将上面的问题转化为所谓的原问题,其最优化解为 p ∗ p^* p∗。
p ∗ = min x max λ , μ , λ i ≥ 0 L ( x , λ , μ ) = min x θ P ( x ) (12) p^* = \min_x \, \max_{\lambda,\mu,\lambda_i \geq 0} L(x,\lambda, \mu) = \min_x \theta_P(x) \tag{12} p∗=xminλ,μ,λi≥0maxL(x,λ,μ)=xminθP(x)(12)
上式第一个等号右边的含义是先固定变量 x x x,将其看成常数,让拉格朗日函数对乘子变量 λ \lambda λ和 μ \mu μ求极大值;消掉(确定了)变量 λ \lambda λ和 μ \mu μ之后,再对变量 x x x求极小值。
为了简化表述,定义如下极大值问题
θ P ( x ) = max λ , μ , λ i ≥ 0 L ( x , λ , μ ) (13) \theta_P(x) =\max_{\lambda,\mu,\lambda_i \geq 0} L(x,\lambda, \mu) \tag{13} θP(x)=λ,μ,λi≥0maxL(x,λ,μ)(13)
这是一个对变量 λ \lambda λ和 μ \mu μ求函数 L L L的极大值的问题,将 x x x看成常数。这样,原始问题被转化为先对变量 λ \lambda λ和 μ \mu μ求极大值,再对 x x x求极小值。
这个原问题和我们要求解的原始问题有同样的解,下面给出证明。对于任意的 x x x,分两种情况讨论。
(1)如果 x x x是不可行解,对于某些 i i i有 g i ( x ) > 0 g_i(x) > 0 gi(x)>0,即 x x x违反了不等式约束条件,我们让拉格朗日乘子 λ i = + ∞ \lambda_i = +\infty λi=+∞,最终使得目标函数 θ P ( x ) = + ∞ \theta_P(x) = +\infty θP(x)=+∞。如果对于某些 i i i有 h i ( x ) ≠ 0 h_i(x) \neq 0 hi(x)=0,即违反了等式约束,我们可以让 μ i = + ∞ ⋅ sgn ( h i ( x ) ) \mu_i = +\infty \cdot \text{sgn}(h_i(x)) μi=+∞⋅sgn(hi(x)),从而使得 θ P ( x ) = + ∞ \theta_P(x) = +\infty θP(x)=+∞。
即对于任意不满足等式或不等式约束条件的 x x x, θ P ( x ) \theta_P(x) θP(x)的值是 + ∞ +\infty +∞。
(2)如果 x x x是可行解,这时 θ P ( x ) = f ( x ) \theta_P(x) = f(x) θP(x)=f(x)。因为有 h i ( x ) = 0 h_i(x) =0 hi(x)=0且 g i ( x ) ≤ 0 g_i(x) \leq 0 gi(x)≤0,而我们要求 λ i ≥ 0 \lambda_i \geq 0 λi≥0,因为 θ P ( x ) \theta_P(x) θP(x)的极大值就是 f ( x ) f(x) f(x)。为了达到这个极大值,我们让 λ i \lambda_i λi和 μ i \mu_i μi为 0 0 0,函数 f ( x ) + ∑ i = 1 p μ i h i ( x ) f(x) + \sum_{i=1}^p \mu_i h_i(x) f(x)+∑i=1pμihi(x)的极大值就是 f ( x ) f(x) f(x)。
综上两种情况,问题 θ P ( x ) \theta_P(x) θP(x)和我们要优化的原始问题的关系可以表述为
θ P ( x ) = { f ( x ) g i ( x ) ≤ 0 , h i ( x ) = 0 + ∞ else \theta_P(x) = \begin{cases} f(x) & g_i(x) \leq 0, h_i(x) = 0\\ +\infty & \text{else} \end{cases} θP(x)={f(x)+∞gi(x)≤0,hi(x)=0else
即 θ P ( x ) \theta_P(x) θP(x)是原始优化问题的无约束版本。对于任何不可行的 x x x,有 θ P ( x ) = + ∞ \theta_P(x) = +\infty θP(x)=+∞,从而使得原始问题的目标函数趋向于无穷大,排除掉 x x x的不可行区域,只剩下可行的 x x x组成的区域。
这样我们要求解的带约束优化问题被转化成了对 x x x不带约束的优化问题,并且二者等价。
下面定义对偶问题与其最优解 d ∗ d^* d∗。
d ∗ = max λ , μ , λ i ≥ 0 min x L ( x , λ , μ ) = max λ , μ , λ i ≥ 0 θ D ( λ , μ ) (14) d^* = \max_{\lambda,\mu,\lambda_i \geq 0}\, \min_x L(x,\lambda, \mu) = \max_{\lambda,\mu,\lambda_i \geq 0} \theta_D(\lambda, \mu) \tag{14} d∗=λ,μ,λi≥0maxxminL(x,λ,μ)=λ,μ,λi≥0maxθD(λ,μ)(14)
这里先固定拉格朗日乘子 λ \lambda λ和 μ \mu μ,调整 x x x让拉格朗日函数对 x x x求极小值;然后调整 λ \lambda λ和 μ \mu μ对函数求极大值。
原问题和对偶问题只是改变了求极大值和极小值的顺序,每次操控的变量是一样的。如果原问题和对偶问题都存在最优解,则对偶问题的最优值不大于原问题的最优值,即
d ∗ = max λ , μ , λ i ≥ 0 min x L ( x , λ , μ ) ≤ min x max λ , μ , λ i ≥ 0 L ( x , λ , μ ) = p ∗ (15) d^* =\max_{\lambda,\mu,\lambda_i \geq 0}\, \min_x L(x,\lambda, \mu) \leq \min_x \, \max_{\lambda,\mu,\lambda_i \geq 0} L(x,\lambda, \mu) = p^* \tag{15} d∗=λ,μ,λi≥0maxxminL(x,λ,μ)≤xminλ,μ,λi≥0maxL(x,λ,μ)=p∗(15)
证明,假设原问题的最优解为 x 1 , λ 1 , μ 1 x_1,\lambda_1,\mu_1 x1,λ1,μ1,对偶问题的最优解为 x 2 , λ 2 , μ 2 x_2,\lambda_2,\mu_2 x2,λ2,μ2,由于原问题是先对 ( λ , μ ) (\lambda,\mu) (λ,μ)取极大值,有
L ( x 1 , λ 1 , μ 1 ) ≥ L ( x 1 , λ 2 , μ 2 ) L(x_1,\lambda_1,\mu_1) \geq L(x_1,\lambda_2,\mu_2) L(x1,λ1,μ1)≥L(x1,λ2,μ2)
这里固定 x 1 x_1 x1。
而对偶问题先对 x x x取极小值,有
L ( x 2 , λ 2 , μ 2 ) ≤ L ( x 1 , λ 2 , μ 2 ) L(x_2,\lambda_2,\mu_2) \leq L(x_1,\lambda_2,\mu_2) L(x2,λ2,μ2)≤L(x1,λ2,μ2)
这类变化的只是 x x x。上面两个式子中右边都是一样的,从而有
L ( x 1 , λ 1 , μ 1 ) ≥ L ( x 2 , λ 2 , μ 2 ) L(x_1,\lambda_1,\mu_1) \geq L(x_2,\lambda_2,\mu_2) L(x1,λ1,μ1)≥L(x2,λ2,μ2)
这一结论称为弱对偶定理(Weak Duality)。
原问题最优值和对偶问题最优值的差 p ∗ − d ∗ p^*-d^* p∗−d∗称为对偶间隙。如果原问题和对偶问题有相同的最优解,那么我们就可以把求解原问题转化为求解对偶问题,此时对偶间隙为0,这种情况称为强对偶。
但要满足怎样的条件才能使得 d ∗ = p ∗ d^*=p^* d∗=p∗呢,就是下面阐述的KKT条件。
KKT条件
KKT(Karush-Kuhn-Tucker)条件用于求解带有等式和不等式约束的优化问题,是拉格朗日乘子法的推广。
对于如下带等式约束和不等式约束的优化问题:
minimize f ( x ) s.t. g i ( x ) ≤ 0 , i = 1 , … , m h i ( x ) = 0 , i = 1 , … , n (16) \begin{aligned} &\text{minimize}\quad &&f(x)\\ &\text{s.t.}\quad &&g_i(x) \leq 0,\quad i=1,\dots,m\\ &&&h_i(x) = 0,\quad i=1,\dots,n \end{aligned} \tag{16} minimizes.t.f(x)gi(x)≤0,i=1,…,mhi(x)=0,i=1,…,n(16)
与拉格朗日对偶的做法类似,为其构造拉格朗日乘子函数消掉等式和不等式约束:
L ( x , λ , μ ) = f ( x ) + ∑ i = 1 m μ i g i ( x ) + ∑ i = 1 n λ i h i ( x ) (17) L(x,\lambda,\mu ) = f(x) + \sum_{i=1}^m \mu_i g_i(x) + \sum_{i=1}^n \lambda_i h_i(x) \tag{17} L(x,λ,μ)=f(x)+i=1∑mμigi(x)+i=1∑nλihi(x)(17)
λ \lambda λ和 μ \mu μ称为KKT乘子。
KKT条件包括:
- ∇ x L ( x , λ , μ ) = 0 \nabla_x L(x,\lambda,\mu) = \pmb 0 ∇xL(x,λ,μ)=0
- g i ( x ) ≤ 0 g_i (x) \leq 0 gi(x)≤0
- h i ( x ) = 0 h_i(x) =0 hi(x)=0
- μ i ≥ 0 \mu_i \geq 0 μi≥0
- μ i g i ( x ) = 0 \mu_ig_i(x) =0 μigi(x)=0
其中第三个条件 h i ( x ) = 0 h_i(x) =0 hi(x)=0等式约束和第二个条件 g i ( x ) ≤ 0 g_i (x) \leq 0 gi(x)≤0不等式约束是本身应该满足的约束;第一个条件 ∇ x L ( x , λ , μ ) = 0 \nabla_x L(x,\lambda,\mu) = \pmb 0 ∇xL(x,λ,μ)=0和拉格朗日乘子法相同。
第四个条件称为对偶可行性条件;
第五个条件称为互补松弛条件,而且当一个变量取非零值时,另一个变量必须取零。
KKT条件是取得极值的必要条件,但如果一个优化问题是凸优化问题,则KKT条件是取得极小值的充分条件。
Slater条件
Slater条件:一个凸优化问题如果存在一个候选 x x x使得所有不等式约束都是严格满足的,即对于所有的 i i i都有 g i ( x ) < 0 g_i(x) < 0 gi(x)<0,也就是说,在不等式约束区域内部至少有一个可行点,则存在 ( x ∗ , λ ∗ , μ ∗ ) (x^*,\lambda^*,\mu^*) (x∗,λ∗,μ∗)使得它们同时为原问题和对偶问题的最优解,即
p ∗ = d ∗ = L ( x ∗ , λ ∗ , μ ∗ ) p^*=d^*= L(x^*,\lambda^*,\mu^*) p∗=d∗=L(x∗,λ∗,μ∗)
Slater条件是强对偶成立的充分条件而不是必要条件。
小结
Slater条件和KKT条件都是用来判断最优化问题是否有解的条件。它们之间的关系可以总结如下:
- Slater条件是一种充分条件,当最优化问题满足Slater条件时,会保证强对偶性成立,并且原始问题和对偶问题都存在最优解。具体来说,Slater条件要求不等式约束条件 g i ( x ) ≤ 0 g_i(x) \leq 0 gi(x)≤0 和等式约束条件 h i ( x ) = 0 h_i(x)=0 hi(x)=0 满足严格可行性,即存在一个 x x x使得所有的不等式约束条件 g i ( x ) < 0 g_i(x) < 0 gi(x)<0 均严格成立。
- KKT条件是一组必要条件,可以用于判断某个点是否为最优解。对于有约束的最优化问题,其KKT条件包括互补松弛条件、不等式约束条件的拉格朗日乘子大于等于零以及梯度为零。若最优化问题的解满足KKT条件,则该解是最优解的必要条件。
需要注意的是,Slater条件只是强对偶性的一种充分条件,而不是必要条件。也就是说,如果一个问题不满足Slater条件,仍然有可能存在最优解以及强对偶性。而KKT条件则是最优解的必要条件,但不一定是充分条件,也就是说,一个满足KKT条件的点并不一定是最优解。
因此,在实际求解问题时,我们通常需要结合Slater条件和KKT条件来进行判断,以保证得到的解是可行的、正确的,并且满足约束条件。
最优化方法
梯度下降法
梯度下降法(gradient descent)或最速下降法是求解无约束最优化问题的一种最常用的方法,它的优点是实现简单。梯度下降法是一种迭代算法,每一步需要求解目标函数的梯度向量。
假设 f ( x ) f(x) f(x)是 R n \Bbb R^n Rn是具有一阶连续偏导数的函数。要求解的无约束最优化问题是
min x ∈ R n f ( x ) (18) \min_{x \in \Bbb R^n} f(x) \tag{18} x∈Rnminf(x)(18)
x ∗ x^* x∗表示目标函数 f ( x ) f(x) f(x)的极小值点。
梯度下降法通过选择适当的初值 x ( 0 ) x^{(0)} x(0),不断迭代,更新 x x x的值,进行目标函数的极小化,直到收敛。由于负梯度方向是使函数值下降最快的方向,在迭代的每一步,以负梯度方向更新 x x x的值,从而达到减少函数值的目的。
由于 f ( x ) f(x) f(x)具有一阶连续偏导数,若第 k k k次迭代值为 x ( k ) x^{(k)} x(k),则可将 f ( x ) f(x) f(x)在 x ( k ) x^{(k)} x(k)附近进行一阶泰勒展开:
f ( x ) = f ( x ( k ) ) + g k T ( x − x ( k ) ) (19) f(x) = f(x^{(k)}) + g_k^T(x-x^{(k)}) \tag{19} f(x)=f(x(k))+gkT(x−x(k))(19)
在人工智能高等数学中我们知道在 x = a x=a x=a点的泰勒展开式为:
g ( x ) = f ( a ) + f ′ ( a ) 1 ! ( x − a ) + f ′ ′ ( a ) 2 ! ( x − a ) 2 + f 3 ( a ) 3 ! ( x − a ) 3 + . . . + f n ( a ) n ! ( x − a ) n (20) g(x) = f(a) + \frac{f^\prime(a)}{1!}(x-a) + \frac{f^{\prime\prime}(a)}{2!}(x-a)^2 + \frac{f^3(a)}{3!}(x-a)^3 + ... + \frac{f^n(a)}{n!}(x-a)^n \tag{20} g(x)=f(a)+1!f′(a)(x−a)+2!f′′(a)(x−a)2+3!f3(a)(x−a)3+...+n!fn(a)(x−a)n(20)
这里去掉了高阶项就得到了公式 ( 19 ) (19) (19), g k = g ( x ( k ) ) = ∇ f ( x ( k ) ) g_k=g(x^{(k)})=\nabla f(x^{(k)}) gk=g(x(k))=∇f(x(k))为 f ( x ) f(x) f(x)在 x ( k ) x^{(k)} x(k)的梯度,即一阶偏导。
求出第 k + 1 k+1 k+1次迭代值 x ( k + 1 ) x^{(k+1)} x(k+1):
x ( k + 1 ) ← x ( k ) + λ k p k (21) x^{(k+1)} \leftarrow x^{(k)} + \lambda_k p_k \tag{21} x(k+1)←x(k)+λkpk(21)
其中, p k p_k pk是搜索方向,取负梯度方向 p k = − ∇ f ( x ( k ) ) p_k= -\nabla f(x^{(k)}) pk=−∇f(x(k)), λ k \lambda_k λk是步长,这里由一维搜索确定,即找到 λ k \lambda_k λk使得
f ( x ( k ) + λ k p k ) = min λ ≥ 0 f ( x ( k ) + λ p k ) (22) f(x^{(k)} + \lambda_k p_k) = \min_{\lambda \geq 0} f(x^{(k)} + \lambda p_k) \tag{22} f(x(k)+λkpk)=λ≥0minf(x(k)+λpk)(22)
一维搜索是一种优化算法,也被称为线性搜索。在机器学习中,一维搜索通常是用来确定如何更新模型参数的步长或学习率,以最小化训练数据上的损失函数。
一维搜索可以简单理解为在某个方向上寻找一个合适的步长,使得当前位置向这个方向前进这个步长之后,能够使目标函数(或者损失函数)达到最小值。其实现过程通常是沿着负梯度方向进行搜索,并通过逐步缩小搜索范围和增加精度等方法,找到一个近似的最优解。
因为一维搜索只在一个方向上进行搜索,在复杂的高维问题中很少直接使用,通常会作为其他更复杂优化算法的辅助手段。
梯度下降法算法如下:
输入: 目标函数 f ( x ) f(x) f(x),梯度函数 g ( x ) = ∇ f ( x ) g(x) = \nabla f(x) g(x)=∇f(x),计算精度 ϵ \epsilon ϵ;
输出: f ( x ) f(x) f(x)的极小点 x ∗ x^* x∗。
(1) 取初值 x ( 0 ) ∈ R n x^{(0)} \in \Bbb R^n x(0)∈Rn,令 k = 0 k=0 k=0。
(2) 计算 f ( x ( k ) ) f(x^{(k)}) f(x(k))。
(3) 计算梯度 g k = g ( x ( k ) ) g_k=g(x^{(k)}) gk=g(x(k)),当 ∣ ∣ g k ∣ ∣ < ϵ ||g_k|| < \epsilon ∣∣gk∣∣<ϵ时,停止迭代,令 x ∗ = x ( k ) x^*=x^{(k)} x∗=x(k);否则,令 p k = − g ( x ( k ) ) p_k=-g(x^{(k)}) pk=−g(x(k)),求 λ k \lambda_k λk使
f ( x ( k ) + λ k p k ) = min λ ≥ 0 f ( x ( k ) + λ p k ) f(x^{(k)} + \lambda_k p_k) = \min_{\lambda \geq 0} f(x^{(k)} + \lambda p_k) f(x(k)+λkpk)=λ≥0minf(x(k)+λpk)
(4) 置 x ( k + 1 ) = x ( k ) + λ k p k x^{(k+1)}=x^{(k)} + \lambda_kp_k x(k+1)=x(k)+λkpk,计算 f ( x ( k + 1 ) ) f(x^{(k+1)}) f(x(k+1))
当 ∣ ∣ f ( x ( k + 1 ) ) − f ( x ( k ) ) ∣ ∣ < ϵ ||f(x^{(k+1)}) - f(x^{(k)})|| < \epsilon ∣∣f(x(k+1))−f(x(k))∣∣<ϵ或 ∣ ∣ x ( k + 1 ) − x ( k ) ∣ ∣ < ϵ ||x^{(k+1)} - x^{(k)}|| < \epsilon ∣∣x(k+1)−x(k)∣∣<ϵ时,停止迭代,令 x ∗ = x ( k + 1 ) x^*=x^{(k+1)} x∗=x(k+1)。
(5) 否则,置 k = k + 1 k=k+1 k=k+1,转(3)。
当目标函数是凸函数时,梯度下降法的解释全局最优解。但一般情况下,其解不保证是全局最优解。且收敛速度也未必是很快的。
如果是无约束优化问题,想要收敛速度快的话,可以考虑牛顿法或拟牛顿法。
牛顿法和拟牛顿法都是求解无约束最优化问题的常用方法,具有收敛速度快的优点。牛顿法是迭代算法,每一步需要求解目标函数的海森矩阵的逆矩阵,计算比较复杂,而且有时候海森矩阵不一定存在逆阵。拟牛顿法通过正定矩阵近似海森矩阵的逆矩阵或海森矩阵,简化了这一计算过程。
相关文章:

最优化简明版(上)
引言 本文简单地介绍一些凸优化(Convex Optimization)的基础知识,可能不会有很多证明推导,目的是能快速应用到机器学习问题上。 凸集 直线与线段 设 x 1 ≠ x 2 x_1 \neq x_2 x1x2为 R n \Bbb R^n Rn空间中的两个点,那么具有下列形…...

MySQL的一些介绍
1. SQL的select语句完整的执行顺序 SQL Select语句完整的执行顺序: 1、from子句组装来自不同数据源的数据; 2、where子句基于指定的条件对记录行进行筛选; 3、group by子句将数据划分为多个分组; 4、使用聚集函数进行计算&am…...

unity发布webGL后无法预览解决
众所周知,unity发布成webgl后是无法直接预览的。因为一般来说浏览器默认都是禁止webgl运行的。 直接说我最后的解决方法:去vscode里下载一个live server ,安装好。 下载vscode地址Visual Studio Code - Code Editing. Redefined 期间试过几种方法都不管…...
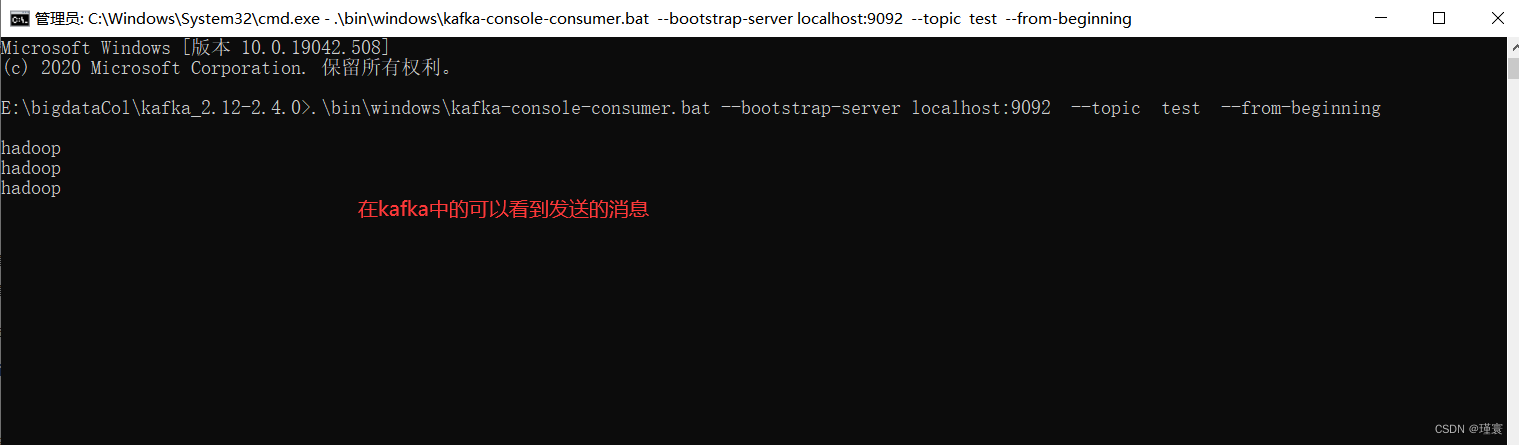
Flume和Kafka的组合使用
一.安装Kafka 1.1下载安装包 通过百度网盘分享的文件:复制链接打开「百度网盘APP 即可获取」 链接:https://pan.baidu.com/s/1vC6Di3Pml6k1KMbnK0OE1Q?pwdhuan 提取码:huan 也可以访问官网,下载kafka2.4.0的安装文件 1.2解…...
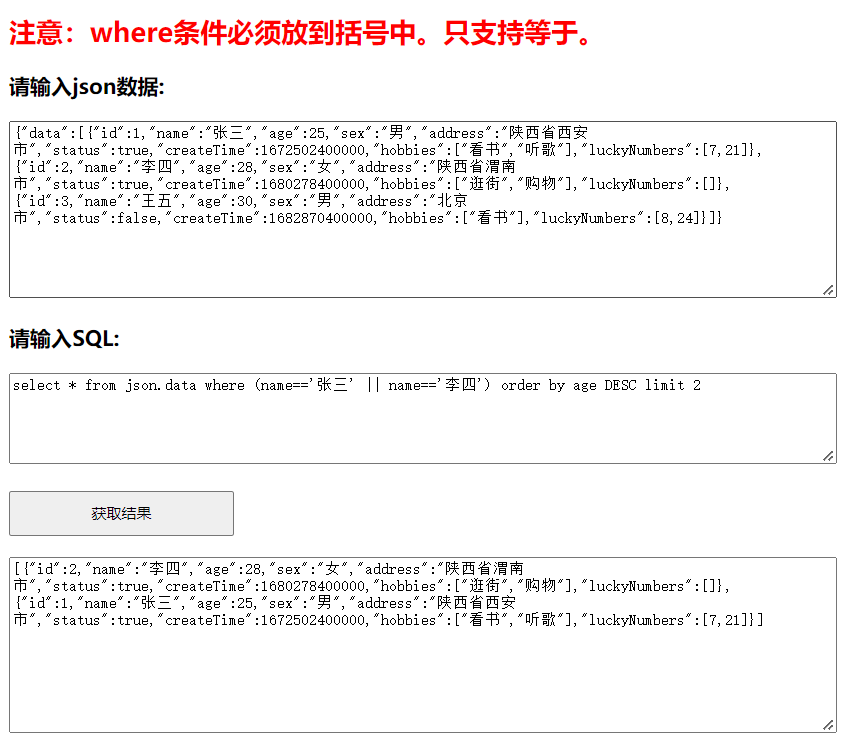
JSONSQL:使用SQL过滤JSON类型数据(支持多种数据库常用查询、统计、平均值、最大值、最小值、求和语法)...
1. 简介 在开发中,经常需要根据条件过滤大批量的JSON类型数据。如果仅需要过滤这一种类型,将JSON转为List后过滤即可;如果相同的条件既想过滤数据库表中的数据、也想过滤内存中JSON数据,甚至想过滤Elasticsearch中的数据ÿ…...
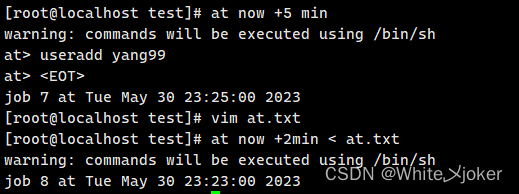
Linux输入输出重定向
目录 Linux输入输出重定向 Linux中的默认设备 输入输出重定向定义 输入输出重定向操作符 实用形式 标准输入、标准输出、标准错误 输出重定向案例 案例1 --- 输出重定向(覆盖) 案例2 --- 输出重定向(追加) 案例3 --- 错误…...
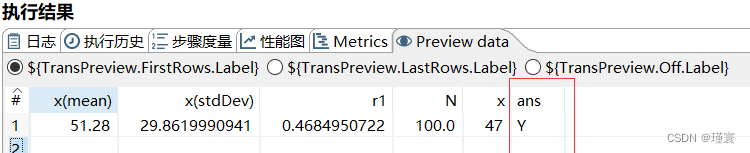
使用kettle进行数据统计
1.使用kettle设计一个能生成100个取值范围为0到100随机整数的转换。 为了完成该转换,需要使用生成记录控件、生成随机数控件、计算器控件及字段选择控件。控件布局如下图所示 生成记录控件可以在限制框内指定生成记录的个数,具体配置如图所示 生成随机数…...

线程的取消和清理
一、线程的取消 意义:随时杀掉一个线程 int pthread_cancel(pthread_t thread); 注意:线程的取消要有取消点才可以,不是说取消就取消,线程的取消点主要是阻塞的系统调用 二、运行段错误调试 可以使用gdb调试 使用gdb 运行代…...

day8 -- 全文本搜索
brief InnoDB存储引擎从MySQL 5.6开始支持全文本搜索。具体来说,MySQL使用InnoDB存储引擎的全文本搜索功能称为InnoDB全文本搜索(InnoDB Full-Text Search)。InnoDB全文本搜索支持标准的全文本搜索查询语法和多语言分词器,因此可…...

C语言:if-else语句
嗨,今天咱们讲讲C语言控制语句里的条件选择,主要总结下if else语句。 咱们生活里经常会有这样的场景,明天该怎么穿呢,得考虑下具体的天气。如果是晴天,温度还不错,可以穿T恤;如果是阴天…...

C语言---函数
1、函数是什么 学习库函数网站: https://cplusplus.com/reference/http://en.cppreference.comhttp://zh.cppreference.com 我们参考文档,学习几个库函数 2、库函数 3、自定义函数 自定义函数和库函数一样,有函数名,返回值类…...
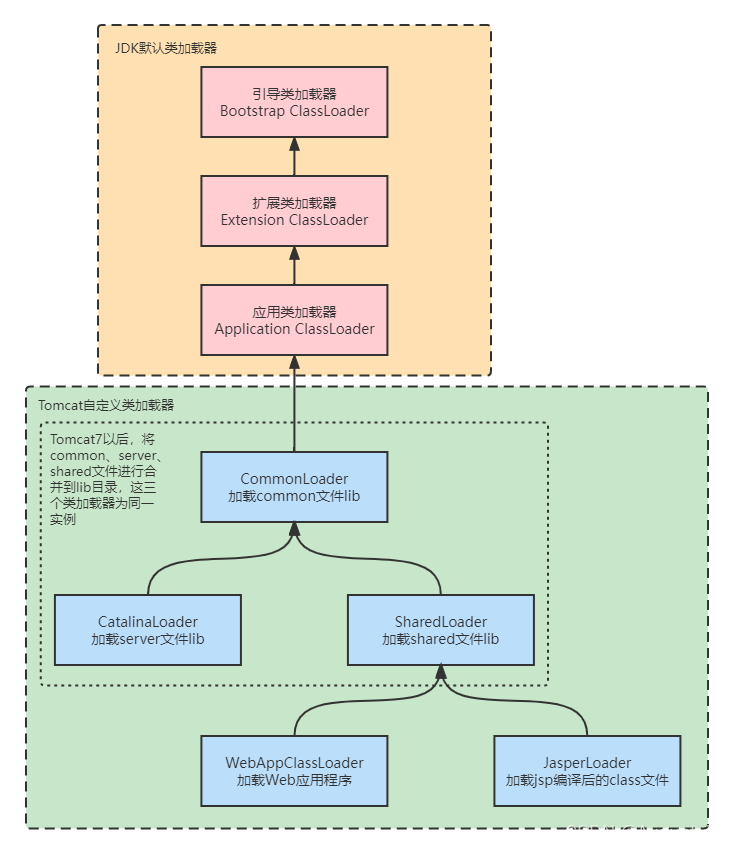
【JVM】什么是双亲委派机制?
一、为什么会有这种机制? 类加载器将.class类加载到内存中时,为了避免重复加载(确保Class对象的唯一性)以及JVM的安全性,需要使用某一种方式来实现只加载一次,加载过就不能被修改或再次加载。 二、什么是双…...

Vulkan Tutorial 7 纹理贴图
目录 23 图像 图片库 暂存缓冲区 纹理图像 布局转换 将缓冲区复制到图像上 准备纹理图像 传输屏障掩码 清除 24 图像视图和采样器 纹理图像视图 采样器 Anisotropy 设备特征 25 组合图像采样器 更新描述符 纹理坐标系 着色器 23 图像 添加纹理将涉及以下步骤&am…...

LinkedBlockingQueue阻塞队列
➢ LinkedBlockingQueue阻塞队列 LinkedBlockingQueue类图 LinkedBlockingQueue 中也有两个 Node 分别用来存放首尾节点,并且里面有个初始值为 0 的原子变量 count 用来记录队列元素个数,另外里面有两个ReentrantLock的独占锁,分别用来控制…...

面试-Redis 常见问题,后续面试遇到新的在补充
面试-Redis 1.谈谈Redis 缓存穿透,击穿,雪崩及如何避免 缓存穿透:是指大量访问请求在访问一个不存在的key,由于key 不存在,就会去查询数据库,数据库中也不存在该数据,无法将数据存储到redis 中…...

2023年上半年数据库系统工程师上午真题及答案解析
1.计算机中, 系统总线用于( )连接。 A.接口和外设 B.运算器、控制器和寄存器 C.主存及外设部件 D.DMA控制器和中断控制器 2.在由高速缓存、主存和硬盘构成的三级存储体系中,CPU执行指令时需要读取数据,那么DMA控制器和中断CPU发出的数据地…...

设计模式概念
设计模式是软件工程领域中常用的解决问题的经验总结和最佳实践。它们提供了一套被广泛接受的解决方案,用于处理常见的设计问题,并促进可重用、可扩展和易于维护的代码。 设计模式的主要目标是提高软件的可重用性、可扩展性和灵活性,同时降低…...

arcpy批量对EXCE经纬度L进行投点,设置为wgs84坐标系,并利用该点计算每个区域内的核密度
以下是在 ArcPy 中批量对 Excel 经纬度 L 进行投点,设置为 WGS84 坐标系,并利用该点计算每个区域内的核密度的详细步骤: 1. 准备数据: 准备包含经纬度信息的 Excel 数据表格,我们假设文件路径为 "C:/Data/locations.xlsx&qu…...
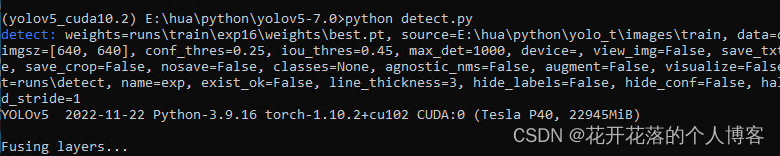
Yolov5训练自己的数据集
先看下模型pt说明 YOLOv5s:这是 YOLOv5 系列中最小的模型。“s” 代表 “small”(小)。该模型在计算资源有限的设备上表现最佳,如移动设备或边缘设备。YOLOv5s 的检测速度最快,但准确度相对较低。 YOLOv5m࿱…...

Bert+FGSM中文文本分类
我上一篇博客已经分别用BertFGSM和BertPGD实现了中文文本分类,这篇文章与我上一篇文章BertFGSM/PGD实现中文文本分类(Loss0.5L10.5L2)_Dr.sky_的博客-CSDN博客的不同之处在于主要在对抗训练函数和embedding添加扰动部分、模型定义部分、Loss函数传到部分…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
