码出高效_第一章 | 有意思的二进制表示及运算
目录
- 0与1的世界
- 1.如何理解32位机器能够同时处理处理32位电路信号?
- 2.如何理解负数的加减法运算
- 3.溢出在运算中如何理解
- 4.计算机种常用的存储单位及转换
- 5.位移运算规则
- 6.有趣的 && 和 &
- 浮点数
- 1.定点小数(为什么会出现浮点数表示?)
0与1的世界
1.如何理解32位机器能够同时处理处理32位电路信号?
设想有8条电路,每条电路有高电平和低电平两种状态,即就有28=256种不同的信号。假设其表示区间为0~255,最大数即28-1。
那么32条电路能够表示最大数为(232-1)=4294967295,即所谓的32位电路信号。
2.如何理解负数的加减法运算
-
正负数表示: 上面的8条电路,最左侧一条表示正负:0-整数,1-负数,不参与数值表示。8条电路表示数值范围 -128~127;
-
二进制整数最终以补码表示: 整数原、反、补码都一样,负数补码为反码加1。
(这样减法运算也可以用加法器实现,使用同一个运算器可减少中间变量的存储开销,降低了CPU内部的设计复杂度,符号位也参与运算)
3.溢出在运算中如何理解
如下图,计算结果需要9条电路表示,用8条电路来表达这个计算结果即溢出。(即在数值运算过程中,超出规定的表示范围)

4.计算机种常用的存储单位及转换
以上示例一条电路线在计算机种被称为1位,即1个bit(简写b)。
8个bit组成一个单位,称一个字节,即1个Byte(简写B)。
1024个Byte(简写为KB);1024个KB(简写为MB);1024个MB(简写为GB)。
5.位移运算规则
补充:
二进制整数最终以补码表示:正数(原、反、补都一样);负数(符号位与原码相同,数值位由原码取反+1)
例如:正数和负数的二进制表示(及十进制转二进制方法)

移动规则:
-
左移右移: 符号位参与移动,除负数向右移动,高位补1之外,其他情况均在空位处补0。
向右移动1位近似表示除以2,但不完全是。十进制奇数转化为二进制后,向右移动时,最右边的1将被直接抹去,即右移对于奇数并非完全相当除以2。
例如111(二进制) = 7(十进制),右移1位:11(二进制) = 3(十进制),这里也解释了除法中的向下取整。
如下图,正数或者负数向左移动的结果可能是正数,也可能是负数。(高位添补规律图示)

-
无符号向右移动 >>>
注意不存在 <<< 无符号向左移动。
向右移动时,正负数高位均补0,正数不断向右移动的最小值是0,而负数不断向右移动的最小值是1。

为何负数不断向右移动最小值是1?(待补充)
6.有趣的 && 和 &
-
按位与(&) 、逻辑与(&&) 和 按位或(|)、逻辑或(||)
区别:&& 有短路功能 ,例如:
/*** 由于&&前边的表达式为false触发短路直接退出,最后结果:a = false ,b = true */ boolean a = true; boolean b = true; boolean c = (a=(1==2)) && (b=(1==2))/*** 最后结果:a = false ,b = false */boolean a = true;boolean b = true;boolean c = (a=(1==2)) & (b=(1==2))同理,按位或(|)对应的逻辑或(||)也有短路的功能
/*** 由于||前边的表达式为true触发短路直接退出,最后结果:e = true ,f = false */boolean e = false;boolean f = false;boolean g = (e=(1==1)) || (f=(1==1))/*** 最后结果:e = true ,f = true*/boolean e = false;boolean f = false;boolean g = (e=(1==1)) || (f=(1==1))注意:逻辑或、逻辑与只能对布尔类型的条件表达式进行运算
-
异或运算 ^
异或运算没有短路功能,其运算:相同为0,不同为1。
例如:1^1=0; 10=1;truetrue=false;…
浮点数
1.定点小数(为什么会出现浮点数表示?)
相关文章:

码出高效_第一章 | 有意思的二进制表示及运算
目录 0与1的世界1.如何理解32位机器能够同时处理处理32位电路信号?2.如何理解负数的加减法运算3.溢出在运算中如何理解4.计算机种常用的存储单位及转换5.位移运算规则6.有趣的 && 和 & 浮点数1.定点小数(为什么会出现浮点数表示?…...
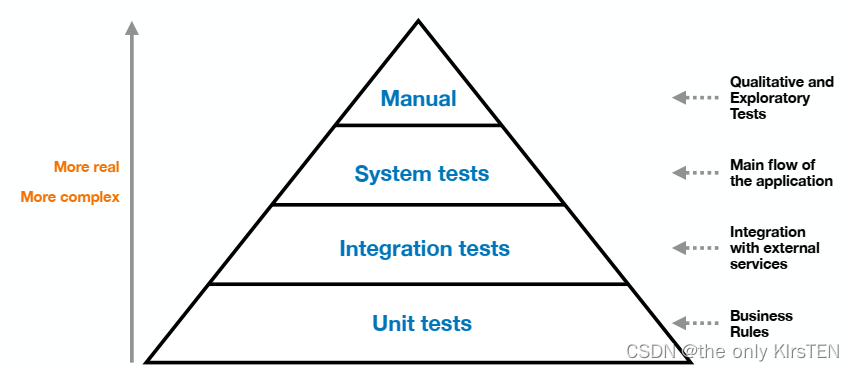
测试类型(单元、集成、系统或手动测试)
测试类型(单元、集成、系统或手动测试) 单元测试 单元是系统的单个组件,例如类或单个方法。孤立地测试单元称为单元测试。 优点:速度快/易控/易写 缺点:缺乏现实性/无法捕获所有错误(例如与其他组件或服务的交互) 单元…...

【笔试强训编程题】Day3.(字符串中找出连续最长的数字串 69385)和(数组中出现次数超过一半的数字 23271)
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:笔试强训编程题 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!! 文章目录…...
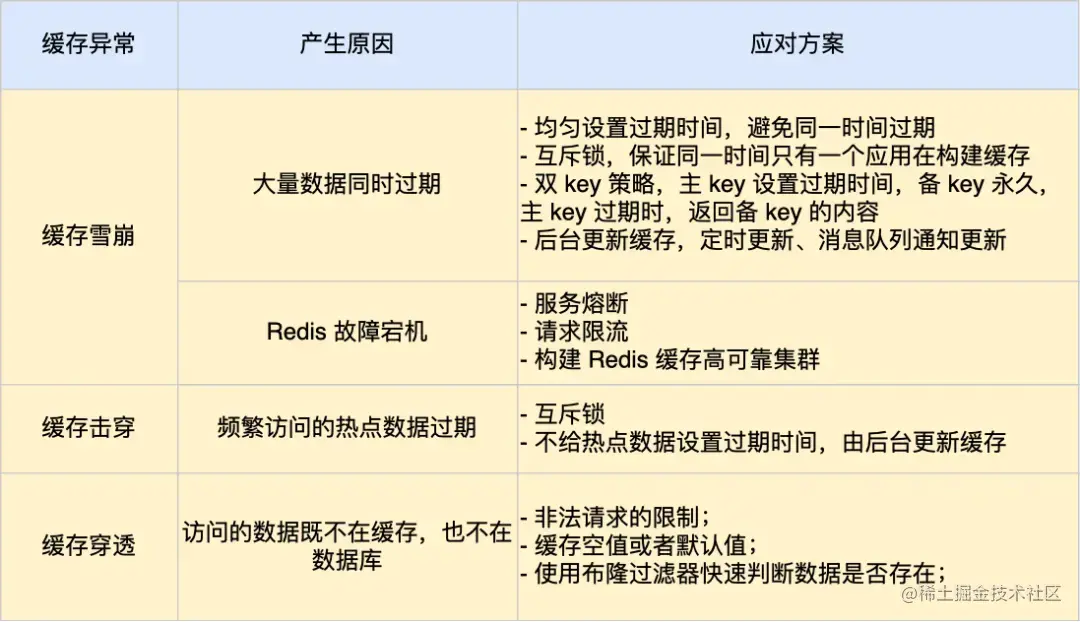
学懂缓存雪崩,缓存击穿,缓存穿透仅需一篇,基于Redis讲解
在了解缓存雪崩、击穿、穿透这三个问题前,我们需要知道为什么我们需要缓存。在了解这三个问题后,我们也必须知道使用Redis时,如何解决这些问题。 所以我将按照"为什么我们需要缓存"、"什么是缓存雪崩、击穿、穿透"、&qu…...

Android 12.0SystemUI 状态栏下拉和通知栏始终居中
1.概述 在12.0的产品定制化开发中,在系统原生的SystemUI 状态栏下拉和通知栏,默认是根据手势的x 坐标的位置居中显示,但是如果太靠两边感觉不太好,下拉太靠边不太好看所以产品提出不管手势在哪里下滑 都要去下拉和通知栏居中显示 会比较好看些 下面就来实现这个需求 2.Sy…...

面向过程编程和面向对象编程的区别
目录 一、面向过程编程 举个栗子: 二、面向对象编程 继续举个栗子: 三、区别 面向过程编程和面向对象编程是两种不同的编程范式,它们在代码的组织和结构上有所不同。 一、面向过程编程 面向过程编程(Procedural Programmin…...

2023年数学与人工智能国际会议——火热征稿中~
会议简介 Brief Introduction 2023年数学与人工智能国际会议(CFMAI 2023) 会议时间:2023年9月22 -24日 召开地点:中国杭州 大会官网:www.cfmai.org 2023年数学与人工智能国际会议(CFMAI 2023)由中山大学主办,CoreShare科享学术交流…...
格式化数字的实用命令:numfmt
在 Linux 系统中,numfmt 是一个用于格式化数字的实用工具。它可以将数字转换为不同的表示方式,如十进制、二进制、字节单位等。本文将详细介绍 numfmt 命令的使用方法,并提供一些适合初学者的示例。 Numfmt 命令语法 numfmt 命令的基本语法如…...

传统的交叉熵函数如何通过平滑处理可以适用于多标签分类任务
传统的交叉熵损失函数通常用于多分类问题,而在多标签分类问题中,每个样本可能属于多个标签,因此需要使用一些新的技术来优化交叉熵损失函数。 一种常用的技术是标签平滑(Label Smoothing),它可以优化传统的…...

关于Netty的一些问题
1.Netty 是什么? Netty是 一个异步事件驱动的网络应用程序框架,用于快速开发可维护的高性能协议服务器和客户端。Netty是基于nio的,它封装了jdk的nio,让我们使用起来更加方法灵活。 2.Netty 的特点是什么? 高并发&…...

Java - ThreadLocal数据存储和传递方式的演变之路
Java - ThreadLocal数据存储和传递方式的演变之路 前言一. InheritableThreadLocal - 父子线程数据传递1.1 父子线程知识预热和 InheritableThreadLocal 实现原理1.2 InheritableThreadLocal 的诟病 二. TransmittableThreadLocal (TTL) 横空出世2.1 跨线程变量传递测试案例2.2…...

vuex三问
文章目录 一、什么是vuex?二、为什么使用vuex?三、如何使用vuex?1.首先安装vuex2.注册vue中3.实例化vuex的store4. 挂载在vue实例上5.在组件中就可以通过this.$store对vuex进行操作。 总结 一、什么是vuex? Vuex 是一个专为 Vue.…...
Selenium自动化测试(基于Java)
目录 一. 了解Selenium ✅1.1 概念 ✅1.2 作用 ✅1.3 特点 ✅1.4 工作原理 二. Selenium Java 环境搭建 ✅2.1 下载 Chrome 浏览器 ✅2.2 查看浏览器的版本 ✅2.3 下载浏览器驱动 ✅2.4 验证环境是否搭建成功 三. Selenium 常用 API ✅3.1 定位元素 ✅3.2 操作对象…...

【网页布局形式----浮动】
网页布局形式----浮动 css浮动:一、常见的三种网页布局形式:1.1 网页布局两大准则: 二 、浮动:2.1 浮动语法:2.2 浮动特性(重难点):浮动元素通常与标准流的父级元素搭配使用…...

人力资源管理的本质
文章目录 写在前面简述用人方面 写在前面 还没写完呢 这是个人理解,本人理工科出身,喜欢直来直去,理论化的知识,苦于市面上的人力书籍资料都不说人话,遂有此文刚入门,甚至没有系统的学习管理知识…...

[NOIP2015 提高组] 运输计划
题目链接 给定一棵树以及树上的 m m m 条通路,我们可以在树上选取一条边,将其权重置为 0 0 0,目标是 min 将某条边权重置 0 max 通路权重 . \min_{将某条边权重置 0}\max 通路权重. 将某条边权重置0minmax通路权重. 20pts(m1) 当…...

【GreendDao 】RxQuery根据指定条件查询,完成后处理UI逻辑
GreenDao 和 RxJava 结合使用可以更方便地处理数据查询和 UI 逻辑的交互。RxQuery 使得一次查询结果可以直接转化成 Observable,而通过 RxJava 的操作符,可以方便地完成异步查询和 UI 逻辑的交互。以下是一个根据指定条件查询数据,查询完成后…...

【C++】unordered_set 和 unordered_map 使用 | 封装
文章目录 1. 使用1. unordered_set的使用2. unordered_map的使用 2. 封装修改结构定义针对insert参数 data的两种情况复用 哈希桶的insertKeyOfT模板参数的作用 迭代器operator()beginendunordered_set对于 begin和end的复用unordered_map对于 begin和end的复用unordered_map中…...

C++环形缓冲区设计与实现:从原理到应用的全方位解析
C环形缓冲区设计与实现:从原理到应用的全方位解析 一、环形缓冲区基础理论解析(Basic Theory of Circular Buffer)1.1 环形缓冲区的定义与作用(Definition and Function of Circular Buffer)1.2 环形缓冲区的基本原理&…...

阿里云服务器部署flask简单方法
记录如何在阿里云服务器上部署flask接口并实现公网访问。 文章目录 1. 简介2. 部署python3环境3. 生成requirement.txt4. 将项目打包上传5. 安装依赖库6. 查看防火墙7. 测试能否公网访问 1. 简介 因落地通话callback服务测试,需要我写一个测试demo,用于…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
