自然语言处理从入门到应用——自然语言处理的语言模型(Language Model,LM)
分类目录:《自然语言处理从入门到应用》总目录
语言模型(Language Model,LM)(也称统计语言模型)是描述自然语言概率分布的模型,是一个非常基础和重要的自然语言处理任务。利用语言模型,可以计算一个词序列或一句话的概率,也可以在给定上文的条件下对接下来可能出现的词进行概率分布的估计。同时,语言模型是一项天然的预训练任务,在基于预训练模型的自然语言处理方法中起到非常重要的作用,因此这种预训练模型有时也被称为预训练语言模型。本文将主要介绍经典的N元语言模型(N-gram Language Model)。
N元语言模型
语言模型的基本任务是在给定词序列 w 1 , w 2 , ⋯ , w t − 1 w_1, w_2, \cdots, w_{t-1} w1,w2,⋯,wt−1的条件下,对下一时刻 t t t可能出现的词 w t w_t wt的条件概率 P ( w t ∣ w 1 w 2 ⋯ w t − 1 ) P(w_t|w_1w_2\cdots w_{t-1}) P(wt∣w1w2⋯wt−1)进行估计。一般地,把 w 1 , w 2 , ⋯ , w t − 1 w_1, w_2, \cdots, w_{t-1} w1,w2,⋯,wt−1称为 w t w_t wt的历史。例如,对于历史“我喜欢”,希望得到下一个词为“读书”的概率,即: P ( 读书 ∣ 我喜欢 ) P(\text{读书}|\text{我喜欢}) P(读书∣我喜欢))。在给定一个语料库时,该条件概率可以理解为当语料中出现“我喜欢”时,有多少次下一个词为“读书”,然后通过最大似然估计进行计算:
P ( 读书 ∣ 我喜欢 ) = C ( 我喜欢读书 ) C ( 我喜欢 ) P(\text{读书}|\text{我喜欢}) = \frac{C(我喜欢读书)}{C(我喜欢)} P(读书∣我喜欢)=C(我喜欢)C(我喜欢读书)
式中, C ( ⋅ ) C(·) C(⋅)表示相应词序列在语料库中出现的次数(也称为频次)。通过以上的条件概率,可以进一步计算一个句子出现的概率,即相应单词序列的联合概率 P ( w 1 , w 2 , ⋯ , w l ) P(w_1, w_2, \cdots, w_l) P(w1,w2,⋯,wl),式中 l l l为序列的长度。可以利用链式法则对该式进行分解,从而将其转化为条件概率的计算问题,即:
P ( w 1 , w 2 , ⋯ , w l ) = ∏ i = 1 l P ( w i ∣ w 1 w 2 ⋯ w i − 1 ) P(w_1, w_2, \cdots, w_l)=\prod_{i=1}^l{P(w_i|w_1w_2\cdots w_{i-1})} P(w1,w2,⋯,wl)=i=1∏lP(wi∣w1w2⋯wi−1)
然而,随着句子长度的增加, w i ∣ w 1 w 2 ⋯ w i − 1 w_i|w_1w_2\cdots w_{i-1} wi∣w1w2⋯wi−1出现的次数会越来越少,甚至从未出现过,那么 P ( w i ∣ w 1 w 2 ⋯ w i − 1 ) P(w_i|w_1w_2\cdots w_{i-1}) P(wi∣w1w2⋯wi−1)则很可能为0,此时对于概率估计就没有意义了。为了解决该问题,可以假设“下一个词出现的概率只依赖于它前面 n − 1 n−1 n−1个词”,即:
P ( w t ∣ w 1 w 2 ⋯ w t − 1 ) ≈ P ( w t ∣ w t − n + 1 w t − n + 2 ⋯ w t − 1 ) P(w_t|w_1w_2\cdots w_{t-1})\approx P(w_t|w_{t-n+1}w_{t-n+2}\cdots w_{t-1}) P(wt∣w1w2⋯wt−1)≈P(wt∣wt−n+1wt−n+2⋯wt−1)
该假设被称为马尔可夫假设(Markov Assumption)。满足这种假设的模型,被称为N元语法或N元文法(N-gram)模型。特别地,当 N = 1 N=1 N=1时,下一个词的出现独立于其历史,相应的一元语法通常记作unigram。当 N = 2 N=2 N=2时,下一个词只依赖于前1个词,对应的二元语法记作bigram。二元语法模型也被称为一阶马尔可夫链(Markov Chain)。类似的,三元语法假设( N = 3 N=3 N=3)也被称为二阶马尔可夫假设,相应的三元语法记作trigram。 N N N的取值越大,考虑的历史越完整。在unigram模型中,由于词与词之间相互独立,因此它是与语序无关的。以bigram模型为例,上式可转换为:
P ( w 1 , w 2 , ⋯ , w l ) = ∏ i = 1 l P ( w i ∣ w i − 1 ) P(w_1, w_2, \cdots, w_l)=\prod_{i=1}^l{P(w_i|w_{i-1})} P(w1,w2,⋯,wl)=i=1∏lP(wi∣wi−1)
为了使 P ( w i ∣ w i − 1 ) P(w_i|w_{i-1}) P(wi∣wi−1)对于 i = 1 i=1 i=1有意义,可在句子的开头增加一个句首标记“<BOS>”(Begin Of Sentence),并设 w 0 = <BOS> w_0=\text{<BOS>} w0=<BOS>。同时,也可以在句子的结尾增加一个句尾标记“<EOS>”(End Of Sentence),设 w l + 1 = <EOS> w_{l+1}=\text{<EOS>} wl+1=<EOS>。
平滑
虽然马尔可夫假设(下一个词出现的概率只依赖于它前面 n − 1 n−1 n−1个词)降低了句子概率为0的可能性,但是当 n n n比较大或者测试句子中含有未登录词(Out-Of-Vocabulary,OOV)时,仍然会出现“零概率”问题。由于数据的稀疏性,训练数据很难覆盖测试数据中所有可能出现的N-gram,但这并不意味着这些N-gram出现的概率为0。为了避免该问题,需要使用平滑(Smoothing)技术调整概率估计的结果。本文将介绍一种最基本,也最简单的平滑算法——折扣法。折扣法(Discounting)平滑的基本思想是“损有余而补不足”,即从频繁出现的N-gram中匀出一部分概率并分配给低频次(含零频次)的N-gram,从而使得整体概率分布趋于均匀。
加一平滑(Add-one Discounting)是一种典型的折扣法,也被称为拉普拉斯平滑(Laplace Smoothing),它假设所有N-gram的频次比实际出现的频次多一次。例如,对于unigram模型来说,平滑之后的概率可由以下公式计算:
P ( w l ) = C ( w i ) + 1 ∑ w ( C ( w ) + 1 ) = C ( w i ) + 1 N + ∣ V ∣ P(w_l)=\frac{C(w_i) + 1}{\sum_w(C(w) + 1)}=\frac{C(w_i) + 1}{N + |V|} P(wl)=∑w(C(w)+1)C(wi)+1=N+∣V∣C(wi)+1
在实际应用中,尤其当训练数据较小时,加一平滑将对低频次或零频次事件给出过高的概率估计。一种自然的扩展是加 δ \delta δ平滑。在加 δ \delta δ平滑中,假设所有事件的频次比实际出现的频次多 δ \delta δ次,其中 0 ≤ δ ≤ 1 0\leq\delta\leq1 0≤δ≤1。以bigram语言模型为例,使用加 δ \delta δ平滑之后的条件概率为:
P ( w i ∣ w i − 1 ) = C ( w i − 1 w i ) + δ ∑ w ( C ( w i − 1 w i ) + δ ) = C ( w i − 1 w i ) + δ C ( w i − 1 ) + δ ∣ V ∣ P(w_i|w_{i-1})=\frac{C(w_{i-1}w_i)+\delta}{\sum_w(C(w_{i-1}w_i)+\delta)}=\frac{C(w_{i-1}w_i)+\delta}{C(w_{i-1})+\delta|V|} P(wi∣wi−1)=∑w(C(wi−1wi)+δ)C(wi−1wi)+δ=C(wi−1)+δ∣V∣C(wi−1wi)+δ
关于超参数 δ \delta δ的取值,需要用到开发集数据。根据开发集上的困惑度对不同 δ \delta δ取值下的语言模型进行评价,最终将最优的δ用于测试集。由于引入了马尔可夫假设,导致N元语言模型无法对长度超过N 的长距离词语依赖关系进行建模,如果将 N 扩大,又会带来更严重的数据稀疏问题,同时还会急剧增加模型的参数量(N-gram数目),为存储和计算都带来极大的挑战。5.1节将要介绍的神经网络语言模型可以较好地解决N元语言模型的这些缺陷。
语言模型性能评价
衡量一个语言模型好坏的一种方法是将其应用于具体的外部任务(如:机器翻译),并根据该任务上指标的高低对语言模型进行评价。这种方法也被称为“外部任务评价”,是最接近实际应用需求的一种评价方法。但是,这种方式的计算代价较高,实现的难度也较大。因此,目前最为常用的是基于困惑度(Perplexity,PPL)的“内部评价”方式。为了进行内部评价,首先将数据划分为不相交的两个集合,分别称为训练集 D train D^{\text{train}} Dtrain和测试集 D test D^{\text{test}} Dtest,其中 D train D^{\text{train}} Dtrain用于估计语言模型的参数。由该模型计算出的测试集的概率 P ( D test ) P(D^{\text{test}}) P(Dtest)则反映了模型在测试集上的泛化能力。假设测试集 D test = w 1 w 2 ⋯ w N D^{\text{test}}=w_1w_2\cdots w_N Dtest=w1w2⋯wN(每个句子的开始和结束分布增加<BOS>与<EOS>标记),那么测试集的概率为:
P ( D test ) = P ( w 1 w 2 ⋯ w N ) = ∏ i = 1 N P ( w i ∣ w 1 w 2 ⋯ w i − 1 ) \begin{aligned} P(D^{\text{test}}) &= P(w_1w_2\cdots w_N) \\ &= \prod_{i=1}^N P(w_i|w_1w_2\cdots w_{i-1}) \end{aligned} P(Dtest)=P(w1w2⋯wN)=i=1∏NP(wi∣w1w2⋯wi−1)
困惑度则为模型分配给测试集中每一个词的概率的几何平均值的倒数:
PPL ( D test ) = ( ∏ i = 1 N P ( w i ∣ w 1 w 2 ⋯ w i − 1 ) − 1 N \text{PPL}(D^{\text{test}})=(\prod_{i=1}^NP(w_i|w_1w_2\cdots w_{i-1})^{-\frac{1}{N}} PPL(Dtest)=(i=1∏NP(wi∣w1w2⋯wi−1)−N1
对于bigram模型而言:
PPL ( D test ) = ( ∏ i = 1 N P ( w i ∣ w i − 1 ) − 1 N \text{PPL}(D^{\text{test}})=(\prod_{i=1}^NP(w_i|w_{i-1})^{-\frac{1}{N}} PPL(Dtest)=(i=1∏NP(wi∣wi−1)−N1
在实际计算过程中,考虑到多个概率的连乘可能带来浮点数下溢的问题,通常需要将上式转化为对数和的形式:
PPL ( D test ) = 2 − 1 N ∑ i = 1 N log 2 P ( w i ∣ w i − 1 ) \text{PPL}(D^{\text{test}})=2^{-\frac{1}{N}\sum_{i=1}^N\log_2P(w_i|w_{i-1})} PPL(Dtest)=2−N1∑i=1Nlog2P(wi∣wi−1)
困惑度越小,意味着单词序列的概率越大,也意味着模型能够更好地解释测试集中的数据。需要注意的是,困惑度越低的语言模型并不总是能在外部任务上取得更好的性能指标,但是两者之间通常呈现出一定的正相关性。因此,困惑度可以作为一种快速评价语言模型性能的指标,而在将其应用于下游任务时,仍然需要根据其在具体任务上的表现进行评价。
参考文献:
[1] 车万翔, 崔一鸣, 郭江. 自然语言处理:基于预训练模型的方法[M]. 电子工业出版社, 2021.
[2] 邵浩, 刘一烽. 预训练语言模型[M]. 电子工业出版社, 2021.
[3] 何晗. 自然语言处理入门[M]. 人民邮电出版社, 2019
[4] Sudharsan Ravichandiran. BERT基础教程:Transformer大模型实战[M]. 人民邮电出版社, 2023
[5] 吴茂贵, 王红星. 深入浅出Embedding:原理解析与应用实战[M]. 机械工业出版社, 2021.
相关文章:
)
自然语言处理从入门到应用——自然语言处理的语言模型(Language Model,LM)
分类目录:《自然语言处理从入门到应用》总目录 语言模型(Language Model,LM)(也称统计语言模型)是描述自然语言概率分布的模型,是一个非常基础和重要的自然语言处理任务。利用语言模型ÿ…...
【MySql】InnoDB一棵B+树可以存放多少行数据?
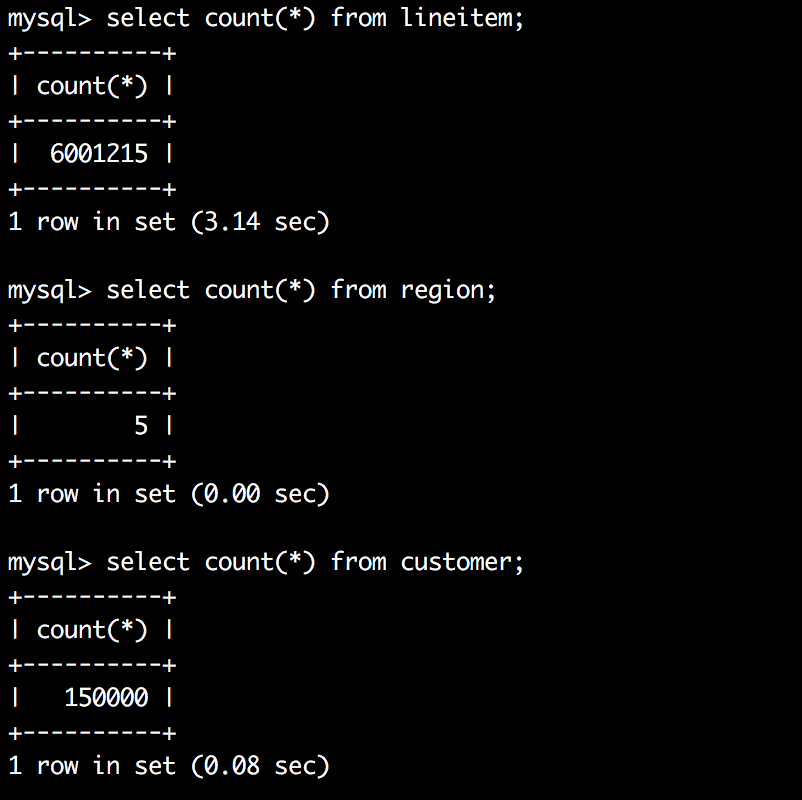
文章目录 背景一、怎么得到InnoDB主键索引B树的高度?二、小结三、最后回顾一道面试题总结参考资料 背景 InnoDB一棵B树可以存放多少行数据?这个问题的简单回答是:约2千万。为什么是这么多呢?因为这是可以算出来的,要搞…...
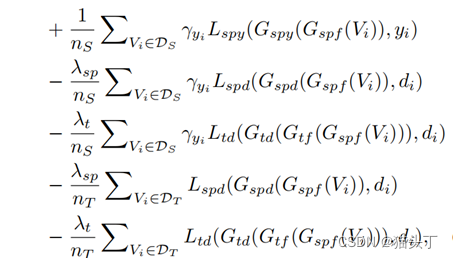
【综述】视频无监督域自适应(VUDA)的小综述
【综述】视频无监督域自适应(VUDA)的小综述 一篇小综述,大家看个乐子就好,参考文献来自于一篇综述性论文 完整PPT已经上传资源:https://download.csdn.net/download/weixin_46570668/87848901?spm1001.2014.3001.550…...

《深入理解计算机系统(CSAPP)》第9章虚拟内存 - 学习笔记
写在前面的话:此系列文章为笔者学习CSAPP时的个人笔记,分享出来与大家学习交流,目录大体与《深入理解计算机系统》书本一致。因是初次预习时写的笔记,在复习回看时发现部分内容存在一些小问题,因时间紧张来不及再次整理…...

信息论与编码 SCUEC DDDD 期末复习
1.证明熵的可加性 2.假设一帧视频图像可以认为是由3*10的五次方个像素组成(每像素均独立变化),如果每个像素可取128个不同的等概率亮度表示。请计算出每帧图像含多少信息量?若有一口述者在约12000个汉字的字汇中选400个字来口述此…...
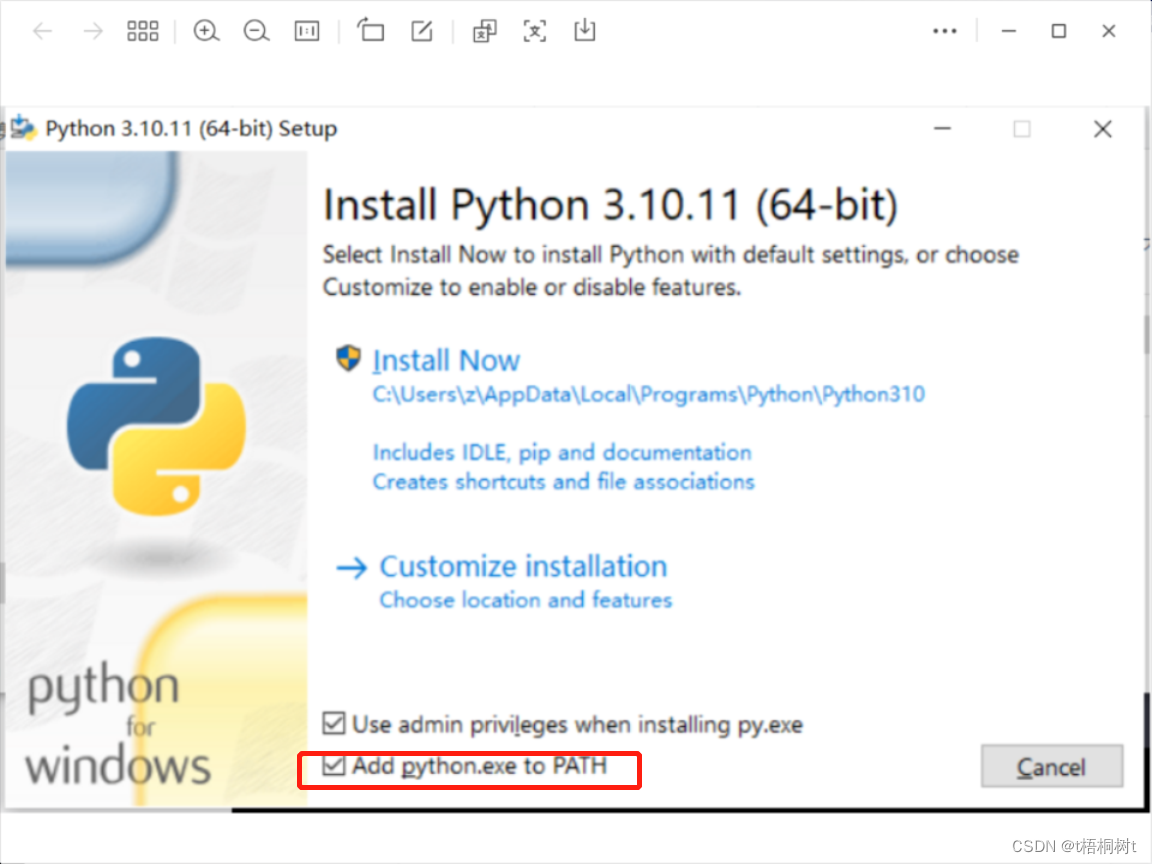
windows安装python开发环境
最近因工作需要,要学习一下python,所以先安装一下python的开发环境,比较简单 下载和安装Python 首先,在浏览器中打开Python的官方网站(https://www.python.org/downloads/) 然后,从该网站下载与你的操…...

java idea常用的快捷方式
文章目录 java idea常用的快捷方式快速复制选多行改变代码格式化 快速代码编辑psvmsout5.forarr.for快速死循环快速补全代码当方法还没创建的时候抽取具有一定功能的代码变成方法 java idea常用的快捷方式 快速复制 c t r l d \color{red}{ctrld} ctrld 选多行改变 A l t 鼠…...

lwIP 开发指南
目录 lwIP 初探TCP/IP 协议栈是什么TCP/IP 协议栈架构TCP/IP 协议栈的封包和拆包 lwIP 简介lwIP 源码下载lwIP 文件说明 MAC 内核简介PHY 芯片介绍YT8512C 简介LAN8720A 简介 以太网接入MCU 方案软件TCP/IP 协议栈以太网接入方案硬件TCP/IP 协议栈以太网接入方案 lwIP 无操作系…...

RabbitMQ消息属性详解
content-type属性 如同各种标准化的HTTP规范,content-type传输消息体的MIME类型。例如,如果你的应用程序正在发送JSON序列化的数据值,那么将content-type属性设置为application/json将允许尚待开发的消费者应用程序在收到消息时检查消息类型…...

shader 混合模式
在所有着色器执行完毕,所有纹理都被应用,所有像素准备被呈现到屏幕之后,使用Blend命令来操作这些像素进行混合。 3.2 blend的语法 BlendOff:关闭blend混合(默认值) BlendSrcFactor DstFactor :配置并启动混…...

【大数据工具】Hive 安装
Hive 环境搭建与基本使用 Hive 安装包下载地址:https://dlcdn.apache.org/hive/ 注:安装 Hive 前要先安装好 MySQL 1. MySQL 安装 MySQL 安装包下载地址:https://dev.mysql.com/downloads/mysql/archives/community/MySQL%20::%20Downloa…...

Android9.0 iptables用INetd实现app某个时间段禁止上网的功能实现
1.前言 在9.0的系统rom定制化开发中,在system中netd网络这块的产品需要中,会要求设置app某个时间段禁止上网的功能,liunx中iptables命令也是比较重要的,接下来就来在INetd这块实现app某个时间段禁止上网的的相关功能,就是在系统中只能允许某个app某个时间段禁止上网,就是…...

webpack.config.js基础配置(五大核心属性)
在上一节webpack零基础入门中我们在安装完webpack 和 webpack-cli依赖之后,直接通过npx webpack ./src/main.js --modedevelopment的方式对src下的js文件进行了打包。 其中的 ./src/main.js: 指定 Webpack 从 main.js 文件开始打包,不但会打包 main.js&a…...
【2023 B卷|200分】)
【华为OD机试】阿里巴巴找黄金宝箱(IV)【2023 B卷|200分】
【华为OD机试】-真题 !!点这里!! 【华为OD机试】真题考点分类 !!点这里 !! 题目描述 一贫如洗的樵夫阿里巴巴在去砍柴的路上,无意中发现了强盗集团的藏宝地, 藏宝地有编号从0-N的箱子,每个箱子上面有一个数字,箱子排列成一个环, 编号最大的箱子的下一个是编号为0的箱…...

Qt6 C++基础入门2 文件结构与信号和槽
目录 标准文件结构widget.hwidget.cppmain.cpppro 文件 信号与槽自定义信号connect 的两种方式 标准文件结构 widget.h widget 对象的头文件 一般会直接在头文件导入所有后续在 cpp 文件内用到的类,所以 include 基本都会写在这里 // 头文件标志起始 #ifndef WID…...
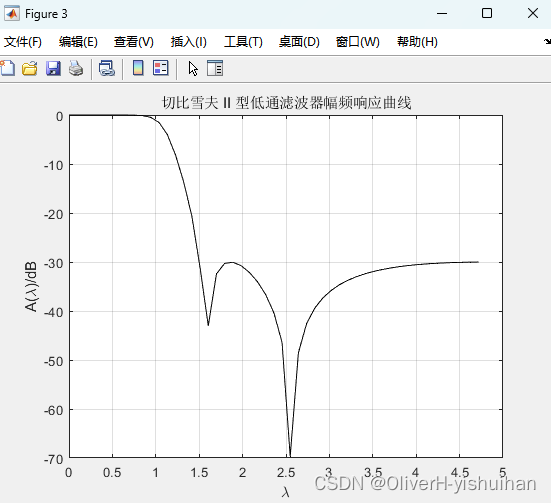
常用模拟低通滤波器的设计——契比雪夫II型滤波器
常用模拟低通滤波器的设计——契比雪夫II型滤波器 切比雪夫 II 型滤波器的振幅平方函数为: 式中,为有效带通截止频率, 是与通带波纹有关的参量, 大,波纹大,; 为 N 阶契比雪夫多项式。 在 Matl…...

SSM 如何使用 Redis 实现缓存?
SSM 如何使用 Redis 实现缓存? Redis 是一个高性能的非关系型数据库,它支持多种数据结构和多种操作,可以用于缓存、队列、计数器等场景。在 SSM(Spring Spring MVC MyBatis)开发中,Redis 可以用来实现数…...

uin-app如何获取微信昵称和头像的博客
在很多应用中都会使用到微信登录功能,这样可以方便用户快速地完成注册、登录等操作。本文将介绍如何通过uin-app获取微信用户的昵称和头像信息。 第一步:准备开发环境 首先,需要下载并安装QQ精简版开发工具(uin-app)…...

第六十七天学习记录:对陈正冲编著《C 语言深度解剖》中关于变量命名规则的学习
最近开始在阅读陈正冲编著的《C 语言深度解剖》,还没读到十分之一就感觉收获颇多。其中印象比较深刻的是其中的变量的命名规则。 里面提到的不允许使用拼音正是我有时候会犯的错。 因为在以往的工作中,偶尔会遇到时间紧迫的情况。 而对于新增加的变量不知…...

matlab 计算点云的线性指数
目录 一、算法原理二、代码实现三、结果展示一、算法原理 选取当前点 p i ( x , y , z ) p_{i}(x,y,z) p<...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
