算法修炼之筑基篇——筑基一层初期(解决01背包问题)
✨博主:命运之光
✨专栏:算法修炼之练气篇
✨博主的其他文章:点击进入博主的主页
前言:学习了算法修炼之练气篇想必各位蒟蒻们的基础已经非常的扎实了,下来我们进阶到算法修炼之筑基篇的学习。筑基期和练气期难度可谓是天差地别,懂得都懂,题目难度相比起练气期的题目难度提升很多,所以要是各位蒟蒻小伙伴们看不懂筑基期的题目可以在练气期多积累积累,练气期的题目也会不断更新,大家一定要把基础打牢固了再来看筑基期的题目哈,这样子也可以提高大家的学习效率,一举两得,加油(●'◡'●)🎉🎉

目录
✨经典的01背包问题
🍓小明的背包1
🍓解题代码
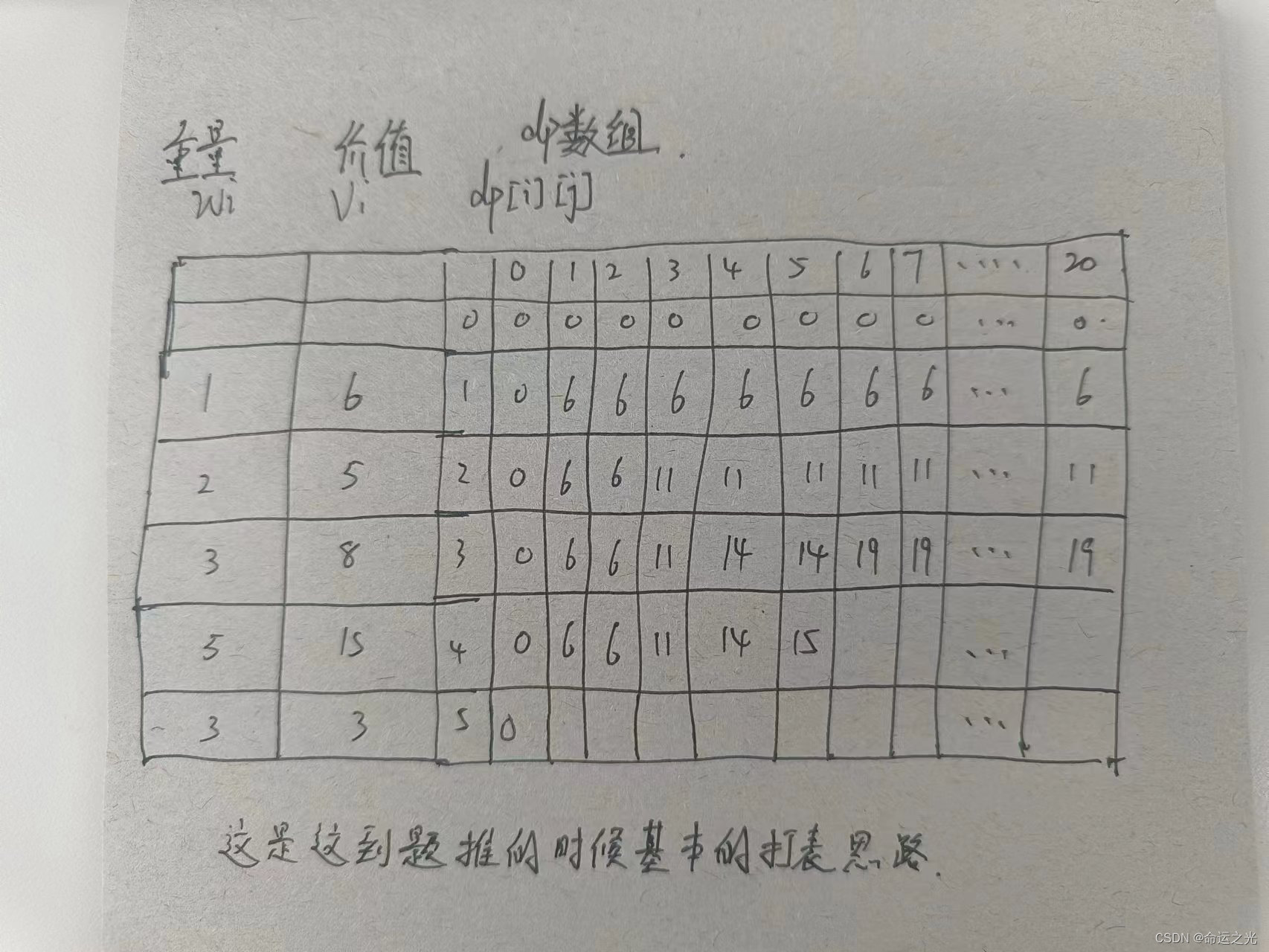
🍓dp数组打表如下:
编辑 ✨经典01背包问题的解题思路
✨01背包的递推公式(重要需要记忆)
✨01背包的递推公式优化为一维数组(重要需要记忆)
✨经典的01背包问题
让我们先看一道经典的01背包问题
🍓小明的背包1
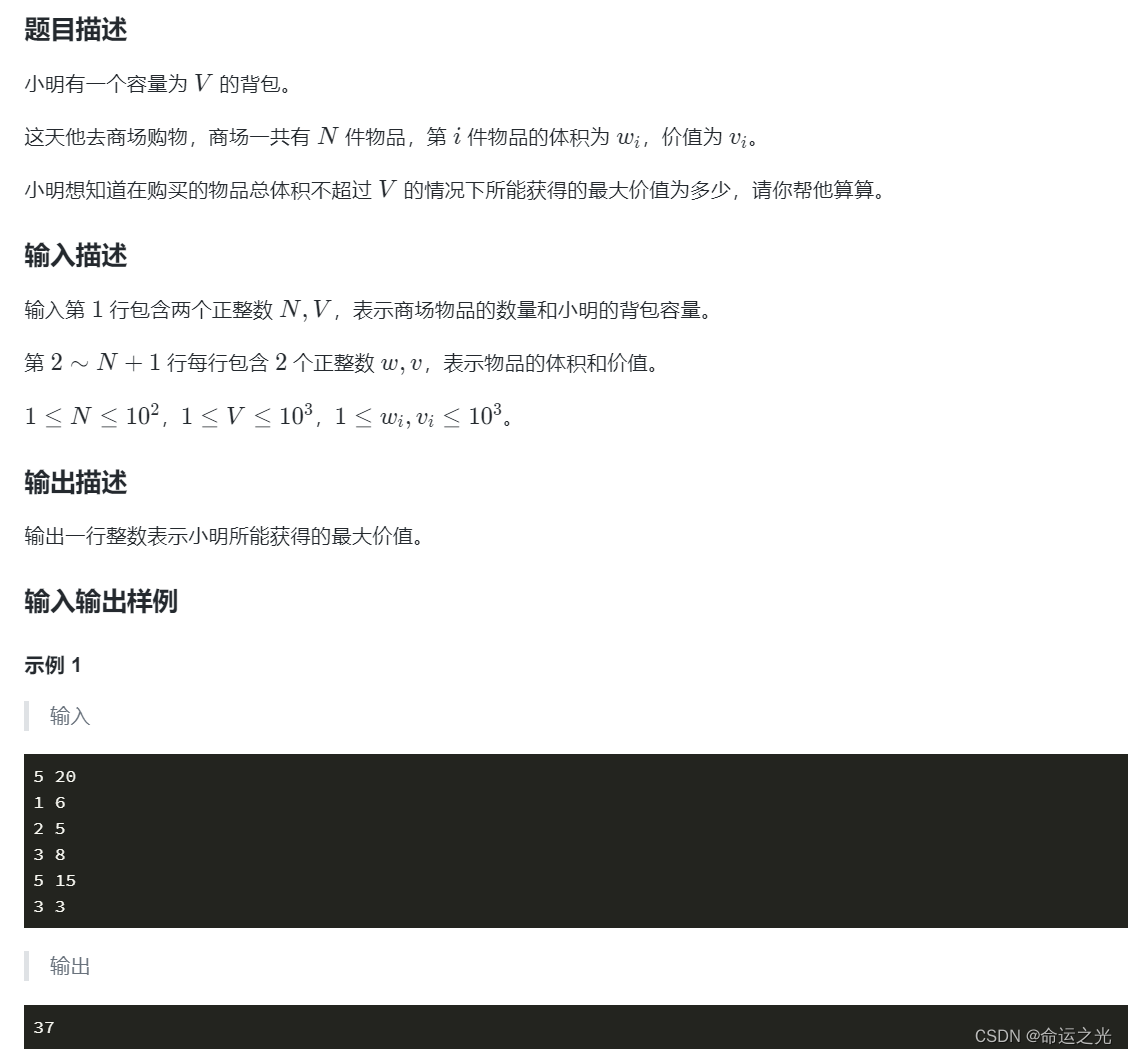
🍓解题代码
#include<bits/stdc++.h>
using namespace std;
int wi[105],vi[105],dp[1005][1005];
int main()
{int n,v;//n为行数,v为背包的大小cin>>n>>v;//传入n,v的值for(int i=1;i<=n;i++){cin>>wi[i]>>vi[i];//传入重量和价值 }//写dp数组int i,j;for(i=1;i<=n;i++){for(j=1;j<=v;j++){if(j<wi[i]){dp[i][j]=dp[i-1][j];//如果重量没j大的话,就直接继承dp数组上一列的最优解,直接dp[i-1][j]即可 }else{//若是比j大则进行比较,这道题标准的01背包问题,直接套用01背包推出的公式即可 dp[i][j]=max(dp[i-1][j],dp[i-1][j-wi[i]]+vi[i]); } }} cout<<dp[n][v];return 0;
}🍓dp数组打表如下:
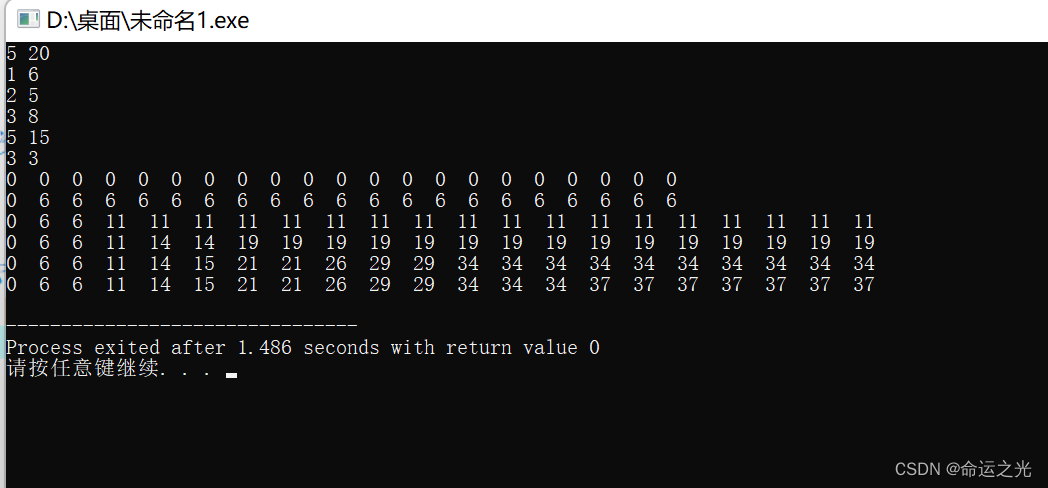 ✨经典01背包问题的解题思路
✨经典01背包问题的解题思路
在C/C++中,可以使用动态规划来解决01背包问题。动态规划是一种常用的解决优化问题的算法思想,它通过将问题分解为子问题,并利用子问题的解来构建更大规模的问题的解。
以下是使用动态规划解决01背包问题的基本步骤:
-
定义问题:我们需要确定背包的容量和物品的重量和价值。假设背包的容量为C,有n个物品,每个物品的重量为w[i],价值为v[i]。
-
创建一个二维数组dp[n+1][C+1],其中dp[i][j]表示在前i个物品中,背包容量为j时的最大价值。
-
初始化边界条件:当物品数量为0或背包容量为0时,最大价值都为0,即dp[i][0] = dp[0][j] = 0。
-
递推关系:对于每个物品i,我们有两种选择:放入背包或不放入背包。如果选择放入背包,那么当前的最大价值为dp[i][j] = dp[i-1][j-w[i]] + v[i];如果选择不放入背包,那么当前的最大价值为dp[i][j] = dp[i-1][j]。我们选择两者中的较大值作为dp[i][j]的值。
-
递推计算:使用循环遍历物品和背包容量,根据递推关系计算dp[i][j]的值。
-
返回结果:dp[n][C]即为问题的解,表示在前n个物品中,背包容量为C时的最大价值。
🍓下面是一个示例代码,演示了如何使用动态规划解决01背包问题:
#include <iostream>
using namespace std;int knapsack(int C, int weights[], int values[], int n) {int dp[n + 1][C + 1];// 初始化边界条件for (int i = 0; i <= n; i++)dp[i][0] = 0;for (int j = 0; j <= C; j++)dp[0][j] = 0;// 计算最大价值for (int i = 1; i <= n; i++) {for (int j = 1; j <= C; j++) {if (weights[i - 1] <= j) {dp[i][j] = max(values[i - 1] + dp[i - 1][j - weights[i - 1]], dp[i - 1][j]);} else {dp[i][j] = dp[i - 1][j];}}}return dp[n][C];
}int main() {int C = 10; // 背包容量int weights[] = {2, 3, 4, 5}; // 物品重量int values[] = {3, 4, 5, 6}; // 物品价值int n = sizeof(weights) / sizeof(weights[0]); // 物品数量int max_value = knapsack(C, weights, values, n);cout << "最大价值:" << max_value << endl;return 0;
}
在这个示例中,背包的容量C为10,有4个物品,重量分别为2、3、4和5,价值分别为3、4、5和6。运行程序将输出最大价值为10,即当背包容量为10时,从这些物品中选择可以得到的最大价值。你可以根据实际情况修改输入的背包容量、物品重量和价值,来解决不同的01背包问题。
✨01背包的递推公式(重要需要记忆)
dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])
其中,dp[i][j]表示在前i个物品中,背包容量为j时的最大价值,w[i]表示第i个物品的重量,v[i]表示第i个物品的价值。
递推公式的含义是,在考虑第i个物品时,我们有两种选择:
- 不选择第i个物品,即仅考虑前i-1个物品,此时的最大价值为
dp[i-1][j]。 - 选择第i个物品,那么背包的容量就会减少,变为
j-w[i],此时的最大价值为dp[i-1][j-w[i]] + v[i],即在考虑前i-1个物品、背包容量为j-w[i]时的最大价值,再加上第i个物品的价值v[i]。
我们选择上述两种选择中的较大值作为dp[i][j]的值,即表示在考虑前i个物品、背包容量为j时的最大价值。
需要注意的是,上述递推公式中的dp数组是一个二维数组,大小为(n+1) x (C+1),其中n表示物品的数量,C表示背包的容量。初始化时,需要设置边界条件,即dp[0][j] = dp[i][0] = 0,表示当物品数量为0或背包容量为0时的最大价值为0。
✨01背包的递推公式优化为一维数组(重要需要记忆)
dp[j] = max(dp[j], dp[j-w[i]] + v[i])
其中,dp[j]表示背包容量为j时的最大价值,w[i]表示第i个物品的重量,v[i]表示第i个物品的价值。
相关文章:

算法修炼之筑基篇——筑基一层初期(解决01背包问题)
✨博主:命运之光 ✨专栏:算法修炼之练气篇 ✨博主的其他文章:点击进入博主的主页 前言:学习了算法修炼之练气篇想必各位蒟蒻们的基础已经非常的扎实了,下来我们进阶到算法修炼之筑基篇的学习。筑基期和练气期…...

JVM的空间结构
目录 一、概述 二、分类 1.程序计数器区域(Program Counter Register): 2.Java虚拟机栈(Stack): 3.堆区(Heap): 4.方法区(Method Area): 5.本地方法栈(Native Method Stack): 一、概述 JVM分为5个主要区域&…...

图像分割的常用算法
图像分割是指将一幅图像划分成多个子区域或像素集合的过程,其中每个子区域或像素集合具有一定的统计特征或语义信息。图像分割是图像处理中的基础任务,其应用涵盖了医学影像、计算机视觉、机器人技术等多个领域。常用的图像分割算法包括: 1.…...

AI歌手真的可以吗
你听过AI歌手吗?近日,“AI孙燕姿”火遍全网,AI孙燕姿翻唱林俊杰的《她说》、周董的《爱在西元前》、赵雷的《成都》等等歌曲让网友听了直呼:“听了一晚上,出不去了。”你认为AI歌手会取代流行歌手成为主流吗࿱…...

Kubernetes高级存储
Kubernetes高级存储 PV PVC k8s支持的存储系统很多,全部掌握不现实。为了屏蔽底层存储实现的细节,方便用户使用,k8s引入PV和PVC两种资源对象。 PV(Persistent Volume)持久化卷,对底层共享存储的抽象,一般由k8s管理员进…...
云原生之使用Docker部署docker-compose-ui工具
云原生之使用Docker部署docker-compose-ui工具 一、Docker Compose UI介绍二、检查本地docker环境1.检查系统版本2.检查docker状态 三、下载Docker Compose UI镜像四、部署Docker Compose UI服务1.新建安装目录2.创建Docker Compose UI容器3.检查Docker Compose UI容器状态4.查…...

文心一言 vs GPT4
本周真是科技爱好者的狂欢节。GPT4和文心一言接连发布,AI工具已经开始走进千家万户。 拿文心一言发布会上的几个问题调戏了 GPT4 一下,看看表现如何。 第一个为文心的回答,第二个为GPT4 的回答。 1. 可以总结一下三体的核心内容吗…...

Tcl-5. format 命令
format 命令和 C 语言中的 printf 和 sprintf 命令类似。它根据一组格式说明来格式化字符 串。此命令不会改变被操作字符串的内容。 [语法]:format spec value1 value2 ... spec 变元包含了格式说明关键词和附加文字。使用%来引入一个关键词,后跟 0 个…...
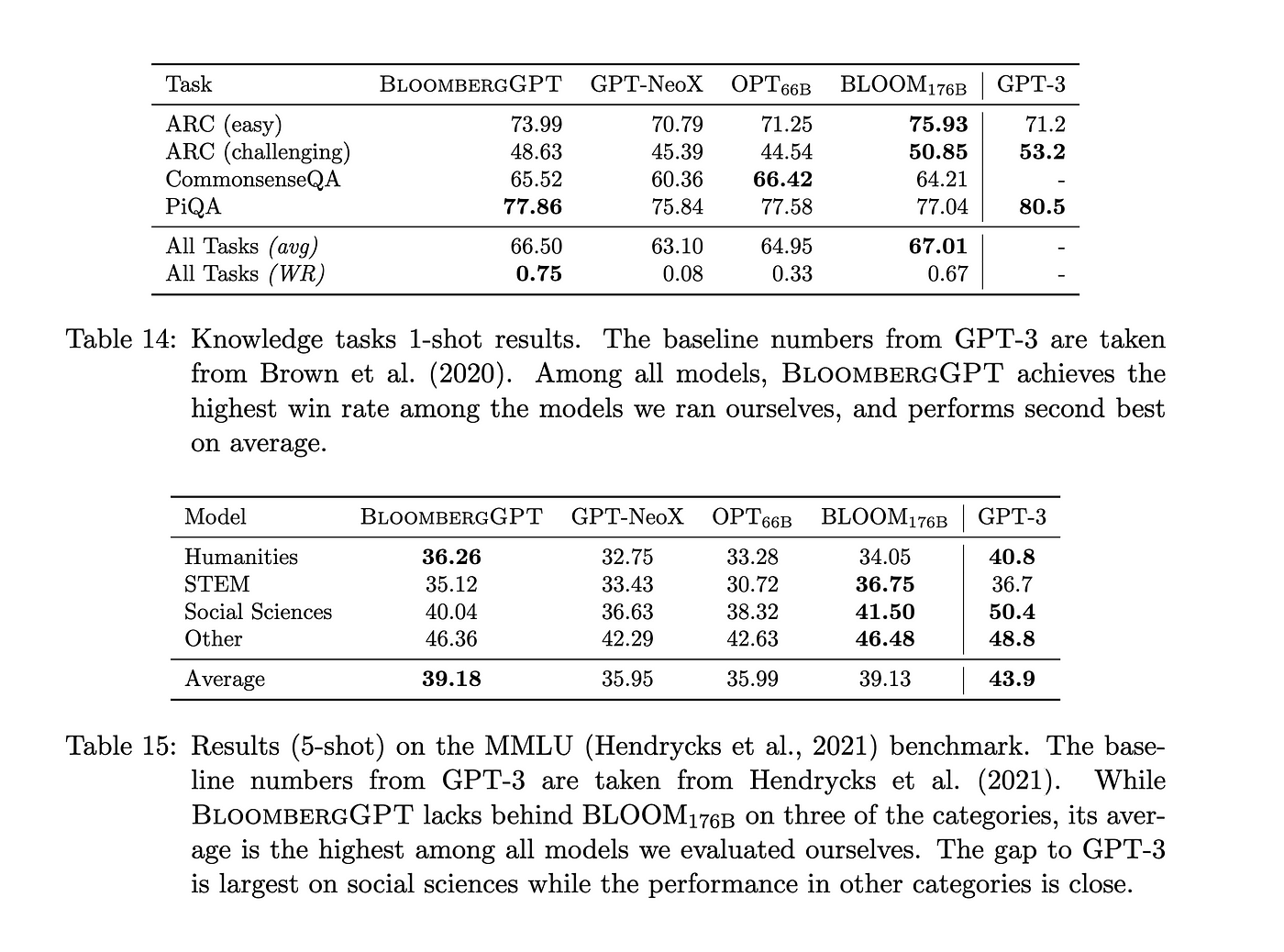
BloombergGPT: 首个金融垂直领域大语言模型
BloombergGPT: 首个金融垂直领域大语言模型 Bloomberg 刚刚发布了一篇研究论文,详细介绍了他们最新的突破性技术 BloombergGPT。BloombergGPT是一个大型生成式人工智能模型,专门使用大量金融数据进行了训练,以支持金融行业自然语言处理 (NLP…...
CMake深度解析:掌握add_custom_command,精通Makefile生成规则
CMake深度解析:掌握add_custom_command,精通Makefile生成规则 1. CMake简介与基础知识1.1 CMake的基本概念(CMake Basic Concepts)1.1.1 项目(Project)1.1.2 目标(Target)1.1.3 命令…...
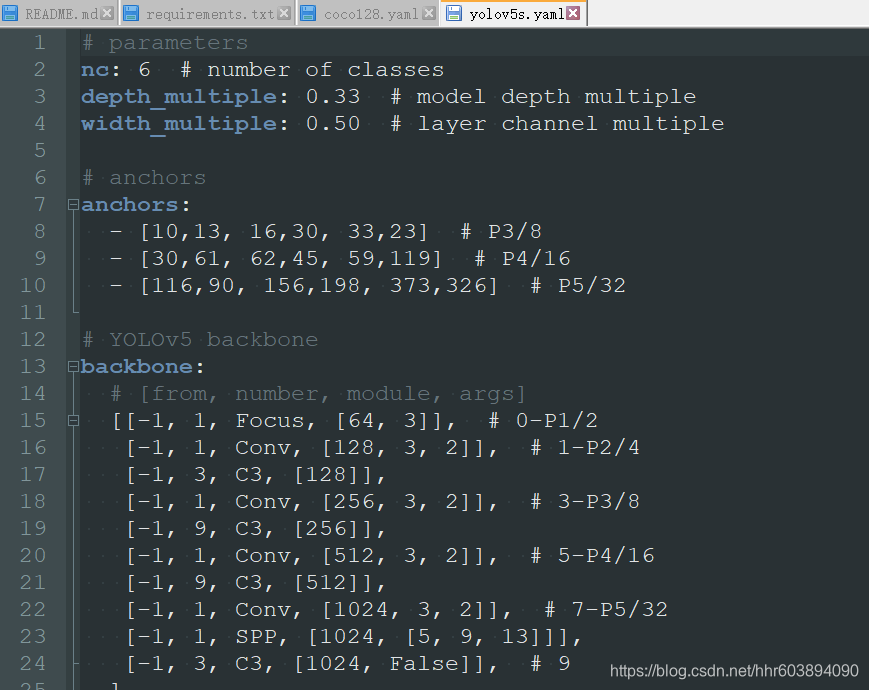
基于Yolov5目标检测的物体分类识别及定位(二) -- yolov5运行环境搭建及label格式转换
刚开始跟着网上的教程做,把环境安装错了,后来直接用GitHub的官方教程来安装环境。 地址是yolov5官方团队代码及教程,看readme文件就可以。 系列文章: 基于Yolov5目标检测的物体分类识别及定位(一) -- 数据集…...
Office project 2019安装
哈喽,大家好。今天一起学习的是project 2019的安装,Microsoft Office project项目管理工具软件,凝集了许多成熟的项目管理现代理论和方法,可以帮助项目管理者实现时间、资源、成本计划、控制。有兴趣的小伙伴也可以来一起试试手。…...

【leetcode-mysql】1251. 平均售价
题目: Table: Prices ---------------------- | Column Name | Type | ---------------------- | product_id | int | | start_date | date | | end_date | date | | price | int | ---------------------- (product_id,start_date,end_dat…...

Razor代码复用
1.布局(Layout)复用 Layout的使用,就像WebForm的模板页一样,甚至会更加简单,更加方便和明了。 要使用Layout,首先要在模板页相应的位置添加RenderBody()方法: <!DOCTYPE html><html la…...
PRL:上海交大张文涛团队实现量子材料相关突破
来源:上海交通大学 近期,上海交通大学物理与天文学院张文涛研究组利用自行研制的高能量和高时间分辨率角分辨光电子能谱系统对量子材料1T-TiSe₂电子结构进行了超快激光操控研究。利用超快光激发与电荷密度波相有关的相干声子,引起晶格内原子…...

impala中group_concat()函数无法对内容进行order by
描述: 使用的是impala数据库,假设有四笔数据,是无序的,业务上要求将其行转列成一行数据,并且里面的数据要按从小到大排序。 过程: 猜测: 数据库Oracle、Mysql、MSsql等支持group_concat中使…...

MySQL 数据库全局变量中文解释
NameValueauto_increment_incrementAUTO_INCREMENT 字段值的自增长步长值。auto_increment_offsetAUTO_INCREMENT 字段值的初始值。autocommit指示新连接的默认提交模式是否启用。automatic_sp_privileges控制是否在存储过程上创建或更改时自动分配特定权限。back_log在开始拒绝…...
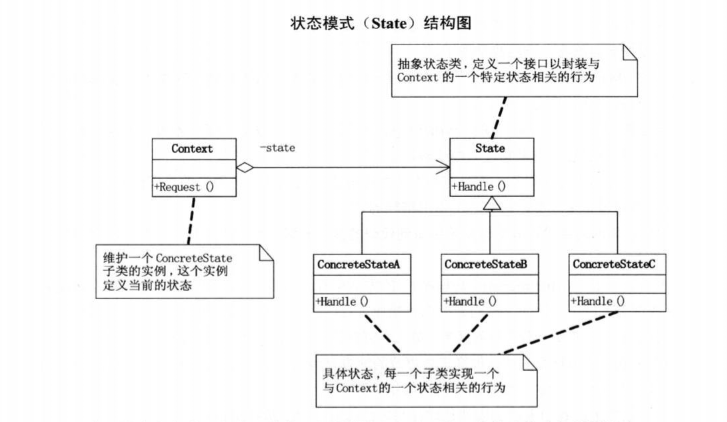
设计模式之~状态模式
状态模式(State),当一个对象的内部状态改变时允许改变其行为,这个对象看起来像是改变了其类。 能够让程序根据不同的外部情况来做出不同的响应,最直接的方法就是在程序中将这些 可能发生的外部情况全部考虑到ÿ…...

【21JavaScript break 和 continue 语句】JavaScript中的break和continue语句:控制循环流程的关键技巧
JavaScript break 和 continue 语句 在JavaScript中,break和continue是两个关键字,用于控制循环结构的执行流程。 break语句 break语句用于中断循环并跳出循环体,使程序执行流程继续到循环之后的下一行代码。 在for循环中使用break for (…...

【SpringBoot】 设置随机数据 用于测试用例
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 设置随机数据——常用于测试用例 SpringBoot设…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
