css3--nth-child的用法
目录
- 使用CSS nth-child选择器
- 基本用法
- 使用公式
- 从零开始
- 关键点
- 结论
使用CSS nth-child选择器
CSS的 :nth-child 选择器是一个强大的工具,允许我们根据它们在父元素中的位置选择元素。这为我们提供了更大的灵活性来控制页面上的元素。
基本用法
基本形式为 :nth-child(n),其中 n 是一个整数,表示要选择的子元素的位置。例如,.item:nth-child(3) 将选择每个父元素中的第三个 .item 子元素。
.item:nth-child(3) {color: red;
}
使用公式
更复杂的是,你可以使用 an+b 形式的公式,其中 a 和 b 是任何整数,n 是一个计数器,从0开始。例如,:nth-child(2n+1) 会选择所有奇数位置的元素,:nth-child(3n+1) 则会选择第1、4、7…位置的元素。
.item:nth-child(2n+1) {color: green;
}
从零开始
虽然 nth-child 是从1开始计数的(在HTML中,第一个元素的索引为1),但在 an+b 公式中,n 是从0开始的。例如,:nth-child(3n) 会选择第0(不存在)、3、6、9…位置的元素。也就是说,:nth-child(3n) 实际上不会选择任何第0个子元素,因为没有第0个子元素。
.item:nth-child(3n) {background-color: blue;
}
关键点
记住,:nth-child 选择器查看的是元素在其父元素中的位置,而不是它在文档中的位置或它在其类别中的位置。所以,如果你有一个列表,它包含两种不同的类元素,:nth-child 会考虑所有的子元素,而不仅仅是特定的类别。
<ul><li class="odd">1</li><li class="even">2</li><li class="odd">3</li><li class="even">4</li>
</ul>
.odd:nth-child(2n) {color: orange;
}
在上面的例子中,没有 .odd 元素会被染色,因为 nth-child(2n) 实际上在选择所有偶数位置的元素,而 .odd 元素都在奇数位置。
结论
学习和理解 :nth-child 选择器的用法可以使你在编写CSS时更加灵活和高效。希望这篇文章能帮助你更好地理解这个强大的选择器,并在你的下一个项目中找到它的用途
。
相关文章:

css3--nth-child的用法
目录 使用CSS nth-child选择器基本用法使用公式从零开始关键点结论 使用CSS nth-child选择器 CSS的 :nth-child 选择器是一个强大的工具,允许我们根据它们在父元素中的位置选择元素。这为我们提供了更大的灵活性来控制页面上的元素。 基本用法 基本形式为 :nth-c…...
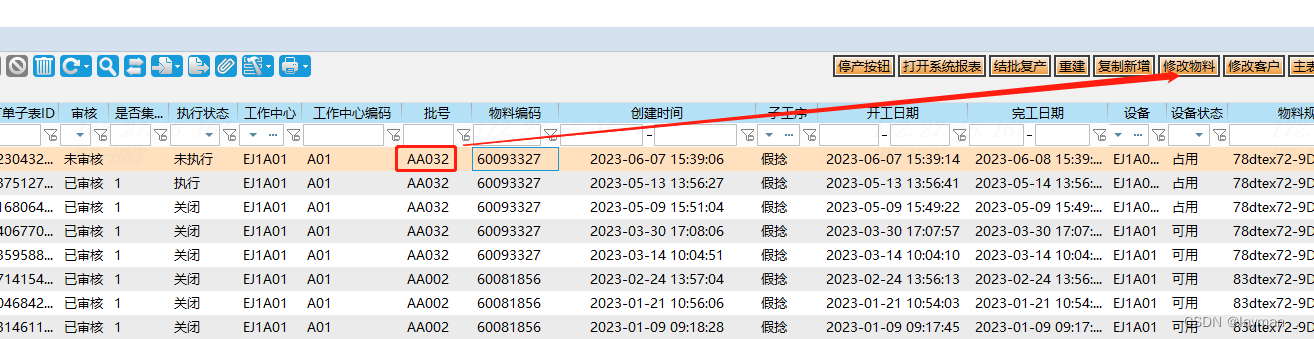
【假捻发加工生产工单下达】
假捻工单是需要下到工作中心的,比如A01机台或者A02机台。 所以下工单之前要先查询A01机台上的最新工单量。 查询结果如下: 她会按照创建时间进行排序,后下的工单排在最前面 (如果下了个新工单,那么前一个工单的执行状态会自动改为关闭。) 因此查询结果,最上面的工单执…...

Go for-range VS for
Go 语言中,for-range 可以用来遍历string、数组(array)、切片(slice)、map和channel,实际使用过程踩了一些坑,所以,还是总结记录下for-range的原理。 首先,go是值传递语言。变量是指针类型,复制指针传递&a…...

大数据教程【01.01】--大数据介绍及开发环境
更多信息请关注WX搜索GZH:XiaoBaiGPT 大数据简介 大数据(Big Data)是指规模庞大、结构复杂、增长速度快且难以使用传统技术处理的数据集合。大数据分析可以帮助企业和组织从海量的数据中提取有价值的信息,用于业务决策、市场分析、…...

文件阅览功能的实现(适用于word、pdf、Excel、ppt、png...)
需求描述: 需要一个组件,同时能预览多种类型文件,一种类型文件可有多个的文件。 看过各种博主的方案,其中最简单的是利用第三方地址进行预览解析(无需任何插件); 这里推荐三个地址:…...

面试-RabbitMQ常见面试问题
1.什么是RabbitMQ? RabbitMQ是一款基于AMQP协议的消息中间件,消费方并不需要确保提供方的存在,实现服务之间的高度解耦。 基本组成有: Queue:消息队列,存储消息,消息送达队列后转发给指定的消费方Exchange:消息队列交…...

使用VBA在单元格中快速插入Unicode符号
Unicode 符号 Unicode 符号在实际工作中有着广泛的应用,比如用于制作邮件签名、文章排版、演示文稿制作等等。在 Excel 表格中,插入符号可以让表格的排版更加美观,同时也能够帮助用户更清晰地表达意思。 Dingbats Dingbats是一个包含装饰符…...

PyTorch 深度学习 || 专题六:PyTorch 数据的准备
PyTorch 数据的准备 1. 生成数据的准备工作 import torch import torch.utils.data as Data#准备建模数据 x torch.unsqueeze(torch.linspace(-1, 1, 500), dim1) # 生成列向量 y x.pow(3) # yx^3#设置超参数 batch_size 15 # 分块大小 torch.manual_seed(10) # 设置种子点…...

迅为RK3568开发板2800页手册+220集视频
iTOP-3568开发板采用瑞芯微RK3568处理器,内部集成了四核64位Cortex-A55处理器。主频高达2.0Ghz,RK809动态调频。集成了双核心架构GPU,ARM G52 2EE、支持OpenGLES1.1/2.0/3.2OpenCL2.0、Vulkan 1.1、内高性能2D加速硬件。 内置NPU 内置独立NP…...

模拟电子 | 稳压管及其应用
模拟电子 | 稳压管及其应用 稳压二极管工作在反向击穿状态时,其两端的电压是基本不变的。利用这一性质,在电路里常用于构成稳压电路。 稳压二极管构成的稳压电路,虽然稳定度不很高,输出电流也较小,但却具有简单、经济实…...

使用大型语言模(LLM)构建系统(二):内容审核、预防Prompt注入
今天我学习了DeepLearning.AI的 Building Systems with LLM 的在线课程,我想和大家一起分享一下该门课程的一些主要内容。 下面是我们访问大型语言模(LLM)的主要代码: import openai#您的openai的api key openai.api_key YOUR-OPENAI-API-KEY def get_…...

springboot---mybatis操作事务配置的处理
目录 前言: 事务的相关问题 1、什么是事务? 2、事务的特点(ACID) 3、什么时候想到使用事务? 4、通常使用JDBC访问数据库,还是mybatis访问数据库,怎么处理事务? 5、问题中事务处…...

游戏盾是什么防御DDOS攻击的
游戏盾是一种专门用于防御分布式拒绝服务(DDoS)攻击的安全工具。DDoS攻击是指攻击者利用大量的计算机或设备同时向目标服务器发送海量的请求,以使目标服务器超负荷运行,无法正常提供服务。游戏盾通过一系列智能的防护措施…...

java快速结束嵌套循环
java快速结束嵌套循环 快速结束for循环 out:for (int i 0; i < 5; i) {in:for (int j 0; j < 5; j) {if (j 2) {break out;}System.out.println("i " i " j " j);}}解释 将外层for循环起别名 o u t \color{red}{out} out,将内层for循环起别名…...

chatgpt赋能python:Python屏蔽一段代码
Python屏蔽一段代码 在Python编程中,有时我们需要屏蔽一段代码以便于调试或者测试。在很多情况下,我们可能不想删除这段代码,因为需要在将来的某个时间再次使用它。为了解决这个问题,我们可以使用Python中的注释语句或者条件语句…...
项目跑不起来
Sa-Token/sa-token-core/src/main/java/cn/dev33/satoken/temp/SaTempUtil.java:10:8 java: 写入cn.dev33.satoken.temp.SaTempUtil时出错: Output directory is not specified 写入cn.dev33.satoken.temp.SaTempUtil时出错: Output directory is not specified 答案…...
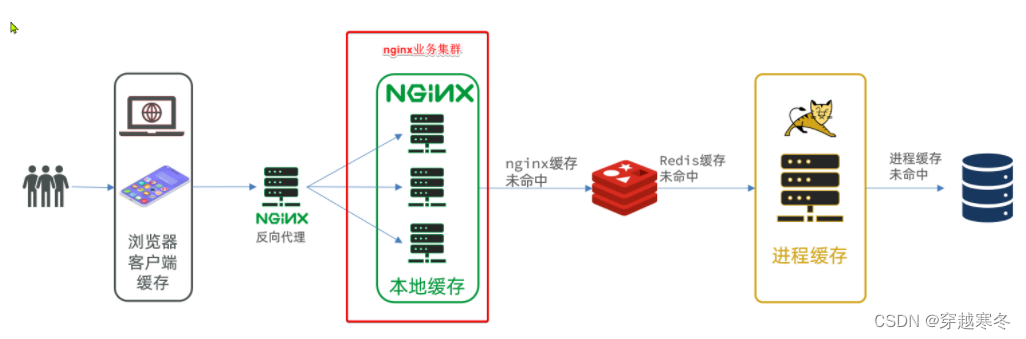
黑马Redis视频教程高级篇(多级缓存案例导入说明)
目录 一、安装MYSQL 1.1、准备目录 1.2、运行命令 1.3、修改配置 1.4、重启 二、导入SQL 三、导入Demo工程 3.1、分页查询商品 3.2、新增商品 3.3、修改商品 3.4、修改库存 3.5、删除商品 3.6、根据id查询商品 3.7、根据id查询库存 3.8、启动 四、导入商品查询…...

2023系统分析师下午案例分析真题
真题1 阅读以下关于软件系统分析与建模的叙述,在纸上回答问题1至3. 说明: 某软件公司拟开发一套汽车租赁系统,科学安全和方便的管理租赁公司的各项业务,提高公司效率,提升利率。注册用户在使用系统镜像车辆预约时需执行以下操作…...

【Python练习】Matplotlib数据可视化
文章目录 一、实验目标二、实验内容1. 用画布的各种设置,绘制类似如图1所示的:y1=sin(x)和y2=cos(x)的曲线图2. 某校高一3班12名同学语数外三科成绩分布情况如表5-2所示,数据值也可以自拟,适当调整。绘制折线图、纵向条形图分析这些同学单科成绩情况,绘制纵向堆叠条形图查…...
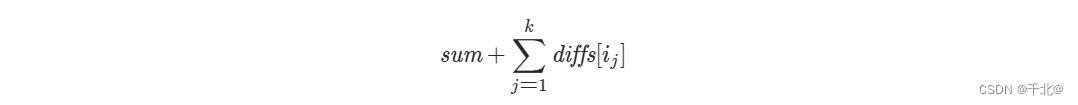
【2611. 老鼠和奶酪】
来源:力扣(LeetCode) 描述: 有两只老鼠和 n 块不同类型的奶酪,每块奶酪都只能被其中一只老鼠吃掉。 下标为 i 处的奶酪被吃掉的得分为: 如果第一只老鼠吃掉,则得分为 reward1[i] 。如果第二…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
