算法笔记-线段树合并
线段树合并
前置知识:权值线段树、动态开点
将两棵线段树的信息合并成一棵线段树。
可以新建一颗线段树保存原来两颗线段树的信息,也可以将第二棵线段树维护的信息加到第一棵线段树上。
前者的空间复杂度较高,如果合并之前的线段树不会再用到的话,可以将第二颗线段树的信息加到第一棵线段树上。
P4556 [Vani有约会]雨天的尾巴 /【模板】线段树合并
题意:
一棵树有 n n n 个点。每次操作 ( x , y , z ) (x,y,z) (x,y,z) 在路径 ( x , y ) (x,y) (x,y) 上的每一个点放一个救济粮 z z z。询问每个点存放最多的是哪种救济粮
解析:
对于树上一条路径上的点进行相同的操作,可以想到树上差分。
然后统计每个点最多的东西,可以用权值线段树维护每种救济粮的数目。
因为将发放救济粮转化成树上差分,求答案的时候需要合并,所以从下向上合并线段树。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
#define debug(x) cerr << #x << ": " << (x) << endl
#define rep(i, a, b) for(int i = (a); i <= (b); i++)
const int maxn = 1e5+10;
const int maxm = 1e5+10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;int head[maxn], tot;
struct edge{int to, nxt;
}e[maxn << 1];
struct node{int mcnt, id;int ls, rs;
}t[maxn * 60];
struct query{int x, y, z;
}q[maxn];int cnt;
int n, m, MAX;
int rt[maxn], ans[maxn];
void add(int a, int b){e[++tot].nxt = head[a];e[tot].to = b;head[a] = tot;
}
int dep[maxn], siz[maxn], top[maxn], son[maxn], fa[maxn];
void dfs1(int u, int p){dep[u] = dep[p] + 1;siz[u] = 1;fa[u] = p;for(int i = head[u]; i; i = e[i].nxt){int v = e[i].to;if(v == p)continue;dfs1(v, u);siz[u] += siz[v];if(siz[v] > siz[son[u]])son[u] = v;}
}
void dfs2(int u, int tp){top[u] = tp;if(son[u])dfs2(son[u], tp);for(int i = head[u]; i; i = e[i].nxt){int v = e[i].to;if(v == fa[u] || v == son[u])continue;dfs2(v, v);}
}
int LCA(int u, int v){while(top[u] != top[v]){if(dep[top[u]] < dep[top[v]])swap(u, v);u = fa[top[u]];}return dep[u] < dep[v] ? u : v;
}
void pushup(int k){if(t[t[k].ls].mcnt >= t[t[k].rs].mcnt){t[k].mcnt = t[t[k].ls].mcnt;t[k].id = t[t[k].ls].id;}else{t[k].mcnt = t[t[k].rs].mcnt;t[k].id = t[t[k].rs].id;}
}
void update(int &k, int l, int r, int pos, int v){if(k == 0)k = ++cnt;if(l == r && l == pos){t[k].mcnt += v;t[k].id = l;return;}int mid = (l+r) >> 1;if(pos <= mid)update(t[k].ls, l, mid, pos, v);elseupdate(t[k].rs, mid+1, r, pos, v);pushup(k);
}
void merge(int &a, int b, int l, int r){if(!a || !b){a = (!a ? b : a);return;} if(l == r){t[a].mcnt += t[b].mcnt;t[a].id = l;return;}int mid = (l+r) >> 1;merge(t[a].ls, t[b].ls, l, mid);merge(t[a].rs, t[b].rs, mid+1, r);pushup(a);
}
void dfs(int u){for(int i = head[u]; i; i = e[i].nxt){int v = e[i].to;if(v == fa[u])continue;dfs(v);merge(rt[u], rt[v], 1, MAX);}if(t[rt[u]].mcnt != 0)ans[u] = t[rt[u]].id;
}
int main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 1, u, v; i < n; i++){cin >> u >> v;add(u, v);add(v, u);}dfs1(1, 0);dfs2(1, 1);for(int i = 1; i <= m; i++){cin >> q[i].x >> q[i].y >> q[i].z;MAX = max(MAX, q[i].z);}for(int i = 1; i <= m; i++){int u = q[i].x, v = q[i].y;int w = q[i].z;int lca = LCA(u, v);update(rt[u], 1, MAX, w, 1);update(rt[v], 1, MAX, w, 1);update(rt[lca], 1, MAX, w, -1);if(fa[lca])update(rt[fa[lca]], 1, MAX, w, -1);}dfs(1);for(int i = 1; i <= n; i++)cout << ans[i] << endl;return 0;
}P1600 [NOIP2016 提高组] 天天爱跑步
题意:
一棵 n n n 节点的树,有 m m m 条路径,每个节点有参数 w i w_i wi。询问有多少条路径的第 w i + 1 w_i+1 wi+1 个点是节点 i i i。
解析:
对于每条路径 ( s , t ) (s, t) (s,t),可以分成两条路径 ( s , l c a ) (s,lca) (s,lca) 和 ( l c a , t ) (lca,t) (lca,t),如果模拟这个过程的话,时间复杂度为 O ( n m ) O(nm) O(nm) 不能接受。
换个角度考虑,对于每个点,有多少条路径会对该点产生贡献。
设节点 i i i 的深度为 d e p i dep_i depi
设路径 ( s , t ) (s,t) (s,t) 对节点 u u u 产生贡献。
- u u u 在 ( s , l c a ) (s,lca) (s,lca) 上。 d e p s − d e p u = w u dep_s-dep_u = w_u deps−depu=wu
- u u u 在 ( l c a , t ) (lca, t) (lca,t) 上。 d e p s + d e p u − 2 d e p l c a = w u dep_s+dep_u-2dep_{lca} = w_u deps+depu−2deplca=wu
即满足条件的路径会对节点 u u u 有贡献。
考虑树上差分,在 s s s 插入 d e p s dep_s deps,在 t t t 处插入 2 d e p l c a − d e p s 2dep_{lca}-dep_s 2deplca−deps,在 l c a lca lca 处插入 − d e p s -dep_s −deps,在 f a ( l c a ) fa(lca) fa(lca) 处插入 d e p s − 2 d e p l c a dep_s-2dep_{lca} deps−2deplca。后两者可以交换,然后线段树合并即可。
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
#define debug(x) cerr << #x << ": " << (x) << endl
#define rep(i, a, b) for(int i = (a); i <= (b); i++)
const int maxn = 3e5+10;
const int maxm = 1e5+10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;int head[maxn], cnt;
struct edge{int to, nxt;
}e[maxn << 1];
struct node{int v;int ls, rs;
}t[maxn * 60];
int n, m;
int rt[maxn], MAX, ans[maxn], w[maxn], tot;
void add(int a, int b){e[++cnt].nxt = head[a];e[cnt].to = b;head[a] = cnt;
}
int siz[maxn], son[maxn], dep[maxn], fa[maxn], top[maxn];
void dfs1(int u, int p){dep[u] = dep[p]+1;siz[u] = 1;fa[u] = p;for(int i = head[u]; i; i = e[i].nxt){int v = e[i].to;if(v == p)continue;dfs1(v, u);siz[u] += siz[v]; if(siz[v] > siz[son[u]])son[u] = v;}
}
void dfs2(int u, int tp){top[u] = tp;if(son[u])dfs2(son[u], tp);for(int i = head[u]; i; i = e[i].nxt){int v = e[i].to;if(v == son[u] || v == fa[u])continue;dfs2(v, v);}
}
int LCA(int u, int v){while(top[u] != top[v]){if(dep[top[u]] < dep[top[v]])swap(u, v);u = fa[top[u]];}return dep[u] < dep[v] ? u : v;
}
void update(int &k, int l, int r, int pos, int v){if(k == 0)k = ++tot;if(l == r && l == pos){t[k].v += v;return;}int mid = (l+r) >> 1;if(pos <= mid)update(t[k].ls, l, mid, pos, v);elseupdate(t[k].rs, mid+1, r, pos, v);return;
}
void merge(int &a, int b, int l, int r){if(!a || !b){a = (!a ? b : a);return;}if(l == r){t[a].v += t[b].v;return;}int mid = (l+r) >> 1;merge(t[a].ls, t[b].ls, l, mid);merge(t[a].rs, t[b].rs, mid+1, r);
}
int query(int k, int l, int r, int pos){if(!k)return 0;if(l == r)return t[k].v;int mid = (l+r) >> 1;if(pos <= mid)return query(t[k].ls, l, mid, pos);elsereturn query(t[k].rs, mid+1, r, pos);
}
void dfs(int u){for(int i = head[u]; i; i = e[i].nxt){int v = e[i].to;if(v == fa[u])continue;dfs(v);merge(rt[u], rt[v], 1, MAX);}if(w[u] && n + dep[u] + w[u] <= MAX)ans[u] += query(rt[u], 1, MAX, n + dep[u] + w[u]);ans[u] += query(rt[u], 1, MAX, n + dep[u] - w[u]);}int main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n >> m;MAX = n << 1;int u, v;for(int i = 1; i < n; i++){cin >> u >> v;add(u, v);add(v, u);}dfs1(1, 0);dfs2(1, 1);for(int i = 1; i <= n; i++)cin >> w[i];for(int i = 1; i <= m; i++){cin >> u >> v;int lca = LCA(u, v);update(rt[u], 1, MAX, n + dep[u], 1);update(rt[v], 1, MAX, n + dep[lca] * 2 - dep[u], 1);update(rt[lca], 1, MAX, n + dep[u], -1);update(rt[fa[lca]], 1, MAX, n + dep[lca] * 2 - dep[u], -1);}dfs(1);for(int i = 1; i <= n; i++)cout << ans[i] << " ";cout << endl;return 0;
}P3224 [HNOI2012]永无乡
题意:
有 n n n 个节点,每个节点有互不相同的重要程度。两种操作:
- 在 ( x , y ) (x,y) (x,y) 之间建桥
- 询问与节点 x x x 所在连通块中重要程度排名第 k k k 小的节点编号
解析:
查询第 k k k 小,考虑权值线段树;维护联通性,考虑并查集。在合并两个连通块时,也合并权值线段树
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define fi first
#define se second
#define debug(x) cerr << #x << ": " << (x) << endl
#define rep(i, a, b) for(int i = (a); i <= (b); i++)
const int maxn = 3e5+10;
const int maxm = 1e5+10;
const int INF = 0x3f3f3f3f;
typedef pair<int, int> pii;struct node{int sum, id;int ls, rs;
}t[maxn * 60];
int rt[maxn];
int tot, n, m, q;
int fa[maxn];
int find(int x){return fa[x] == x ? x : fa[x] = find(fa[x]);
}
int pushup(int k){t[k].sum = t[t[k].ls].sum + t[t[k].rs].sum;
}
void update(int &k, int l, int r, int pos, int idx){if(k == 0)k = ++tot;if(l == r){t[k].sum++;t[k].id = idx;return;}int mid = (l+r) >> 1;if(pos <= mid)update(t[k].ls, l, mid, pos, idx);elseupdate(t[k].rs, mid+1, r, pos, idx);pushup(k);
}
void merge(int &a, int b, int l, int r){if(!a || !b){a = (a == 0 ? b : a);return;}if(l == r){t[a].sum += t[b].sum;return;}int mid = (l+r) >> 1;merge(t[a].ls, t[b].ls, l, mid);merge(t[a].rs, t[b].rs, mid+1, r);pushup(a);
}
int query(int a, int k, int l, int r){if(t[a].sum < k || !a)return 0;if(l == r)return t[a].id;int mid = (l+r) >> 1;int ans = 0;if(k <= t[t[a].ls].sum)ans = query(t[a].ls, k, l, mid);elseans = query(t[a].rs, k-t[t[a].ls].sum, mid+1, r);return ans;
}
int main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 1, p; i <= n; i++){fa[i] = i;cin >> p;update(rt[i], 1, n, p, i);}for(int i = 1, x, y; i <= m; i++){cin >> x >> y;int fx = find(x);int fy = find(y);fa[fy] = fx;merge(rt[fx], rt[fy], 1, n);}cin >> q;string op;for(int i = 1, x, y; i <= q; i++){cin >> op >> x >> y;if(op == "B"){int fx = find(x);int fy = find(y);if(fx == fy)continue;fa[fy] = fx;merge(rt[fx], rt[fy], 1, n); }else if(op == "Q"){int fx = find(x);int res = query(rt[fx], y, 1, n);if(res == 0)cout << -1 << endl;elsecout << res << endl;}} return 0;
}
相关文章:

算法笔记-线段树合并
线段树合并 前置知识:权值线段树、动态开点 将两棵线段树的信息合并成一棵线段树。 可以新建一颗线段树保存原来两颗线段树的信息,也可以将第二棵线段树维护的信息加到第一棵线段树上。 前者的空间复杂度较高,如果合并之前的线段树不会再用…...

Fiddler抓取IOS数据包实践教程
Fiddler是一个http协议调试代理工具,它能够记录并检查所有你的电脑和互联网之间的http通讯,设置断点,查看所有的“进出”Fiddler的数据(指cookie,html,js,css等文件)。 本章教程,主要介绍如何利用Fiddler抓取IOS数据包相关教程。 目录 一、打开Fiddler监听端口 二、配置网…...
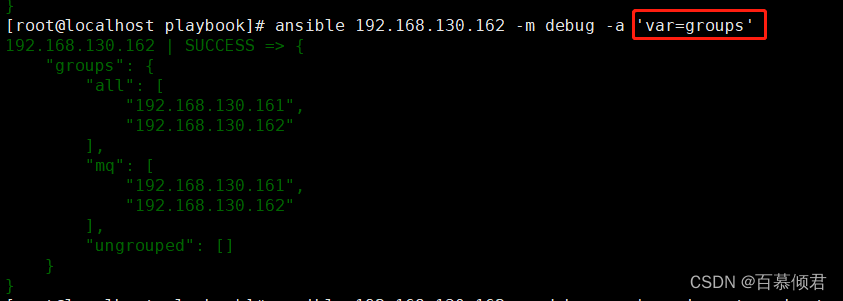
Ansible基础4——变量、机密、事实
文章目录 一、变量二、机密2.1 创建加密文件2.2 查看加密文件2.3 编辑加密文件内容2.4 加密现有文件2.5 解密文件2.6 更改加密密码 三、事实3.1 收集展示事实3.2 展示某个结果3.3 新旧事实命令3.4 关闭事实3.5 魔法变量 一、变量 常设置的变量: 要创建的用户要安装的…...

React实现Vue的watch监听属性
在 Vue 中可以简单地使用 watch 来监听数据的变化,还能获取到改变前的旧值,而在 React 中是没有 watch 的。 React中比较复杂,但是我们如果想在 React 中实现一个类似 Vue 的 watch 监听属性,也不是没有办法。 在React类组件中实…...
axios、跨域与JSONP、防抖和节流
文章目录 一、axios1、什么是axios2、axios发起GET请求3、axios发起POST请求4、直接使用axios发起请求 二、跨域与JSONP1、了解同源策略和跨域2、JSONP(1)实现一个简单的JSONP(2)JSONP的缺点(3)jQuery中的J…...
macOS Ventura 13.5beta2 (22G5038d)发布
系统介绍 黑果魏叔 6 月 1 日消息,苹果今日向 Mac 电脑用户推送了 macOS 13.5 开发者预览版 Beta 2 更新(内部版本号:22G5038d),本次更新距离上次发布隔了 12 天。 macOS Ventura 带来了台前调度、连续互通相机、Fac…...
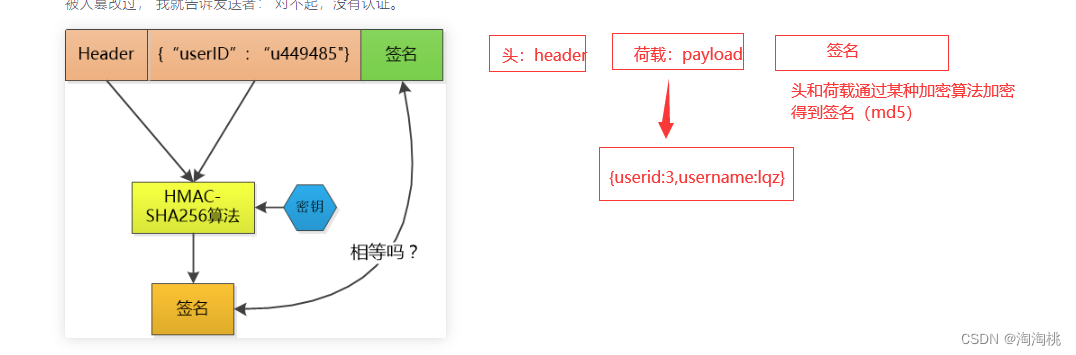
jwt----介绍,原理
token:服务的生成的加密字符串,如果存在客户端浏览器上,就叫cookie -三部分:头,荷载,签名 -签发:登录成功,签发 -认证:认证类中认证 # jwt&…...

Three.js--》实现3d水晶小熊模型搭建
目录 项目搭建 初始化three.js基础代码 加载背景纹理 加载小熊模型 今天简单实现一个three.js的小Demo,加强自己对three知识的掌握与学习,只有在项目中才能灵活将所学知识运用起来,话不多说直接开始。 项目搭建 本案例还是借助框架书写…...

《阿里大数据之路》研读笔记(1)
首先先看到OLAP和OLTP的区别: OLTP(Online transaction processing):在线/联机事务处理。典型的OLTP类操作都比较简单,主要是对数据库中的数据进行增删改查,操作主体一般是产品的用户或者是操作人员。 OLAP(Online analytical processing):…...

Logback 日志框架详解
一、Logback 简介 Logback 是一个日志框架,旨在成为 log4j 的替代品。它由 Ceki Glc 创建并维护,是一款开源的日志框架,是 slf4j(Simple Logging Facade for Java)的实现。相比于 log4j,Logback 具有更高的…...

BIO、NIO、AIO 有什么区别?
BIO (Blocking I/O): Block IO 同步阻塞式 IO ,传统 IO,特点是模式简单、使用方便,并发处理能力低。 同步阻塞 I/O 模式,数据的读取写入必须阻塞在一个线程内等待其完成,在活动连接数不是特别高(…...

nginx和tomcat负载均衡、静态分离
tomcat重要目录 bin 存放启动和关闭Tomcat脚本conf存放Tomcat不同的配置文件doc存放Tomcat文档lib存放Tomcat运行需要的库文件logs存放Tomcat执行时的log文件src存放Tomcat的源代码webappsTomcat的主要Web发布目录work存放jsp编译后产生的class文件 nginx负载均衡原理 nginx实…...

用AI写出的高考作文!
今天是6月7日,又到了每一年高考的日子。小灰自己参加高考是在2004年,距离现在已经将近20年,现在回想起来,真的是恍如隔世。 今天高考语文的作文题是什么呢? 全国甲卷的题目是:人技术时间 人们因技术发展得以…...

chatgpt赋能python:Python屏幕输入介绍:了解命令行输入的基本知识
Python屏幕输入介绍:了解命令行输入的基本知识 Python是一种使用广泛的编程语言,用于编写各种类型的应用程序,包括图形用户界面应用程序和基于命令行的应用程序。对于基于命令行的应用程序来说,屏幕输入非常重要。本文将介绍Pyth…...

bert中文文本摘要代码(1)
bert中文文本摘要代码 写在最前面关于BERT使用transformers库进行微调 load_data.py自定义参数collate_fn函数BertDataset类主函数 tokenizer.py创建词汇表encode函数decode函数 写在最前面 熟悉bert+文本摘要的下游任务微调的代码,方便后续增加组件实现…...

为何溃坝事故频发,大坝安全如何保障?
随着水利水电工程的重要性日益突显,水库大坝安全越来越受到相关部门的重视。因为大坝的安全直接影响水利工程的功能与作用,因此对大坝安全的监测显得十分必要。大坝安全监测的作用是能够及时掌握大坝的运行状态,及时发现大坝的变形、渗漏等异…...
第十九章_手写Redis分布式锁
锁的种类 单机版同一个JVM虚拟机内synchronized或者Lock接口。 分布式多个不同JVM虚拟机,单机的线程锁机制不再起作用,资源类在不同的服务器之间共享了。 一个靠谱分布式锁需要具备的条件和刚需 独占性 :OnlyOne,任何时刻只能有且…...

电路设计【8】原理图中VCC、VDD、VEE、VSS、VBAT各表示什么意思
文章目录 一、名词解析二、应用讲解三、举例分析:为什么stm32vet6中要分出5对VDD VSS?它们分别负责哪些模块的供电? 一、名词解析 (1)VCC:Ccircuit 表示电路的意思, 即接入电路的电压 (2&…...

Volatile、Synchronized、ReentrantLock锁机制使用说明
一、Volatile底层原理 volatile是轻量级的同步机制,volatile保证变量对所有线程的可见性,不保证原子性。 当对volatile变量进行写操作的时候,JVM会向处理器发送一条LOCK前缀的指令,将该变量所在缓存行的数据写回系统内存。由于缓…...

港联证券|AI概念股继续活跃 科创50指数逆势走高
周三,A股市场出现极致分化态势。得益于存储芯片为代表的硬科技股的强势,科创50指数逆势走高。但创业板指、深证成指等主要股指仍然跌跌不休,沪指险守3200点关口。AI概念股继续逆势活跃,国资云、数据方向领涨,算力概念股…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

数据分析六部曲?
引言 上一章我们说到了数据分析六部曲,何谓六部曲呢? 其实啊,数据分析没那么难,只要掌握了下面这六个步骤,也就是数据分析六部曲,就算你是个啥都不懂的小白,也能慢慢上手做数据分析啦。 第一…...
