动态规划-硬币排成线
动态规划-硬币排成线
- 1 描述
- 2 样例
- 2.1 样例 1:
- 2.2 样例 2:
- 2.3 样例 3:
- 3 算法解题思路及实现
- 3.1 算法解题分析
- 3.1.1 确定状态
- 3.1.2 转移方程
- 3.1.3 初始条件和边界情况
- 3.1.4 计算顺序
- 3.2 算法实现
- 3.2.1 动态规划常规实现
- 3.2.2 动态规划滚动数组
该题是lintcode的第394题, https://www.lintcode.com/problem/394/,解题思路参考九章侯老师给的建议。
1 描述
有 n 个硬币排成一条线。两个参赛者轮流从右边依次拿走 1 或 2 个硬币,直到没有硬币为止。拿到最后一枚硬币的人获胜。
请判定 先手玩家 必胜还是必败?
若必胜, 返回 true, 否则返回 false.
Lintcode超级VIP年卡 618预售 享买一年送一年
微信加【jiuzhang1104】备注【VIP】即可参加
2 样例
2.1 样例 1:
输入: 1
输出: true
2.2 样例 2:
输入: 4
输出: true
解释:
先手玩家第一轮拿走一个硬币, 此时还剩三个.
这时无论后手玩家拿一个还是两个, 下一次先手玩家都可以把剩下的硬币拿完.
2.3 样例 3:
输入: 5
输出: true
解释:
先手玩家第一轮拿走两枚硬币, 此时还剩三个.
这时无论后手玩家拿一个还是两个, 下一次先手玩家都可以把剩下的硬币拿完.
3 算法解题思路及实现
3.1 算法解题分析
3.1.1 确定状态
这是一个博弈型动态规划类算法题,这中类型的算法解题分析不是从最后一步分析,而是从第一步分析,原因是随着硬币的减少,问题越来越简单。
假设两名选手分别为A和B,A为硬币为N时的先手,而当A拿走一或则两枚硬币之后,B则成为剩余硬币的先手,因此A要保证在自己拿走1或者2枚硬币的时候至少有一种情况是可以赢的。
子问题就转换为:
面对N枚硬币,A作为先手是不是必胜,
则需要知道面对N - 1和N - 2枚硬币B作为先手是不是必胜,
状态:设f[i]表示面对i个石子,是否先手必胜f[i] = True/False
3.1.2 转移方程
状态:设f[i]表示面对i个石子,是否先手必胜f[i] = True/False

f[i] = (f[i-1] == FALSE OR f[i-2] == FALSE)
3.1.3 初始条件和边界情况
- 设f[i]表示面对i个石子,是否先手必胜f[i] = True/False
- f[i] = (f[i-1] == FALSE OR f[i-2] == FALSE)
- f[0] = FALSE 面对0枚硬币,先手必败
- f[1] = f[2] = True, 面对1枚或2枚硬币,先手必胜
3.1.4 计算顺序
- f[0], f[1], f[2], …, f[N]
- 如果f[N] = true,则先手必胜,否则先手必败
- 时间负责度为O(N)
- 空间复杂度为:O(N)
3.2 算法实现
3.2.1 动态规划常规实现
public class Solution {/*** @param n: An integer* @return: A boolean which equals to true if the first player will win*/public boolean firstWillWin(int n) {// write your code hereif (n <= 0) {return false;}if (n <= 2) {return true;}boolean [] f = new boolean[n + 1];f[0] = false;f[1] = true;for (int i = 2; i <= n; i++) {f[i] = (!f[i - 1] || !f[i - 2]);}return f[n];}
}
3.2.2 动态规划滚动数组
public class Solution {/*** @param n: An integer* @return: A boolean which equals to true if the first player will win*/public boolean firstWillWin(int n) {// write your code hereif (n <= 0) {return false;}if (n <= 2) {return true;}boolean [] f = new boolean[2];f[0] = false;f[1] = true;for (int i = 2; i <= n; i++) {f[i % 2] = !(f[(i -1) % 2] && f[(i - 2) % 2]);}return f[n % 2];}
}
相关文章:

动态规划-硬币排成线
动态规划-硬币排成线 1 描述2 样例2.1 样例 1:2.2 样例 2:2.3 样例 3: 3 算法解题思路及实现3.1 算法解题分析3.1.1 确定状态3.1.2 转移方程3.1.3 初始条件和边界情况3.1.4 计算顺序 3.2 算法实现3.2.1 动态规划常规实现3.2.2 动态规划滚动数组 该题是lintcode的第394题&#x…...
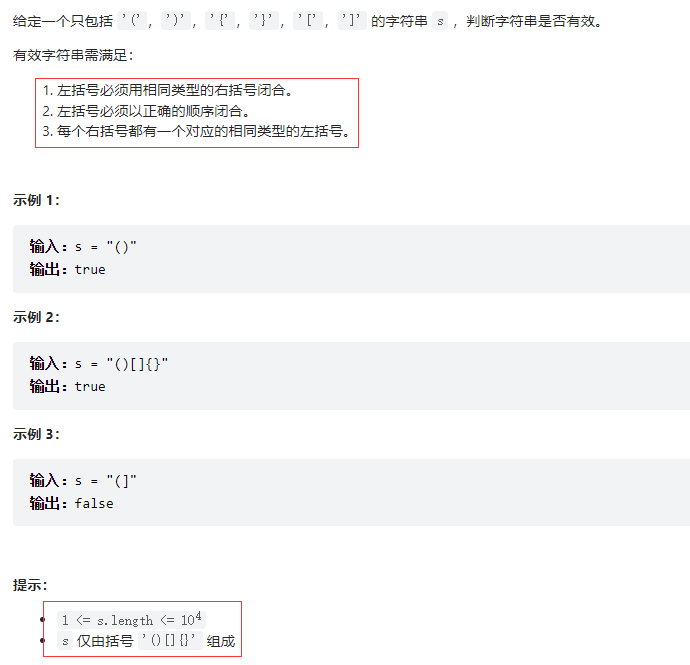
有效的括号——力扣20
题目描述 思路 1.判断括号的有效性可以使用「栈」这一数据结构来解决 2.遍历给定的字符串 s。当遇到一个左括号时,我们会期望在后续的遍历中,有一个相同类型的右括号将其闭合。由于后遇到的左括号要先闭合,因此我们可以将这个左括号放入栈顶。…...

【轻量级网络】华为诺亚:VanillaNet
文章目录 0. 前言1. 网络结构2. VanillaNet非线性表达能力增强策略2.1 深度训练2.2 扩展激活函数 3. 总结4. 参考 0. 前言 随着人工智能芯片的发展,神经网络推理速度的瓶颈不再是FLOPs或参数量,因为现代GPU可以很容易地进行计算能力较强的并行计算。相比…...
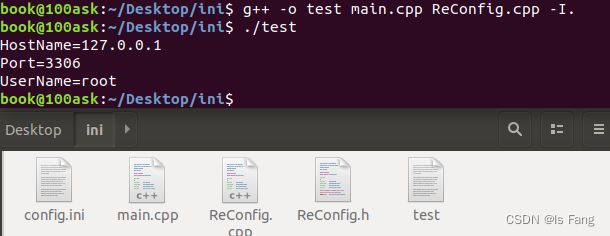
读写ini配置文件(C++)
文章目录 1、为什么要使用ini或者其它(例如xml,json)配置文件?2、ini文件基本介绍3、ini配置文件的格式4、C读写ini配置文件5、 代码示例6、 配置文件的解析库 文章转载于:https://blog.csdn.net/weixin_44517656/article/details/109014236 1、为什么要…...
Python对接亚马逊电商平台SP-API的一些概念理解准备
❝ 除了第三方服务商,其实亚马逊卖家本身也可以通过和SP-API的对接,利用程序来自动化亚马逊店铺销售运营管理中很多环节的工作,简单的应用比如可以利用SP-API的对接,实现亚马逊卖家后台各类报表的定期自动下载以及数据分析整理工…...

[Halcon3D] 主流的3D光学视觉方案及原理
📢博客主页:https://loewen.blog.csdn.net📢欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢本文由 丶布布原创,首发于 CSDN,转载注明出处🙉📢现…...

Go Web下gin框架使用(二)
〇、gin 路由 Gin是一个用于构建Web应用程序的Go语言框架,它具有简单、快速、灵活的特点。在Gin中,可以使用路由来定义URL和处理程序之间的映射关系。 r : gin.Default()// 访问 /index 这个路由// 获取信息r.GET("/index", func(c *gin.Con…...

算法笔记-线段树合并
线段树合并 前置知识:权值线段树、动态开点 将两棵线段树的信息合并成一棵线段树。 可以新建一颗线段树保存原来两颗线段树的信息,也可以将第二棵线段树维护的信息加到第一棵线段树上。 前者的空间复杂度较高,如果合并之前的线段树不会再用…...

Fiddler抓取IOS数据包实践教程
Fiddler是一个http协议调试代理工具,它能够记录并检查所有你的电脑和互联网之间的http通讯,设置断点,查看所有的“进出”Fiddler的数据(指cookie,html,js,css等文件)。 本章教程,主要介绍如何利用Fiddler抓取IOS数据包相关教程。 目录 一、打开Fiddler监听端口 二、配置网…...
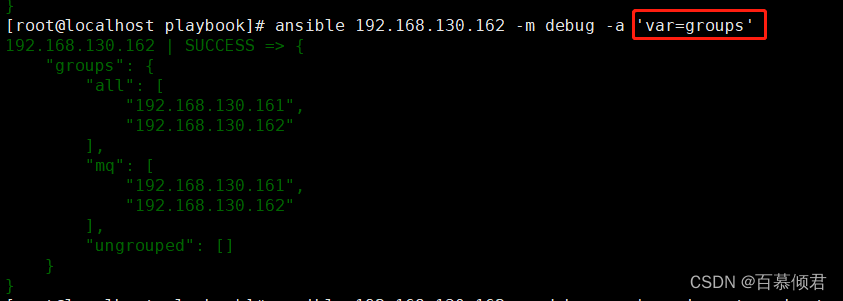
Ansible基础4——变量、机密、事实
文章目录 一、变量二、机密2.1 创建加密文件2.2 查看加密文件2.3 编辑加密文件内容2.4 加密现有文件2.5 解密文件2.6 更改加密密码 三、事实3.1 收集展示事实3.2 展示某个结果3.3 新旧事实命令3.4 关闭事实3.5 魔法变量 一、变量 常设置的变量: 要创建的用户要安装的…...

React实现Vue的watch监听属性
在 Vue 中可以简单地使用 watch 来监听数据的变化,还能获取到改变前的旧值,而在 React 中是没有 watch 的。 React中比较复杂,但是我们如果想在 React 中实现一个类似 Vue 的 watch 监听属性,也不是没有办法。 在React类组件中实…...
axios、跨域与JSONP、防抖和节流
文章目录 一、axios1、什么是axios2、axios发起GET请求3、axios发起POST请求4、直接使用axios发起请求 二、跨域与JSONP1、了解同源策略和跨域2、JSONP(1)实现一个简单的JSONP(2)JSONP的缺点(3)jQuery中的J…...
macOS Ventura 13.5beta2 (22G5038d)发布
系统介绍 黑果魏叔 6 月 1 日消息,苹果今日向 Mac 电脑用户推送了 macOS 13.5 开发者预览版 Beta 2 更新(内部版本号:22G5038d),本次更新距离上次发布隔了 12 天。 macOS Ventura 带来了台前调度、连续互通相机、Fac…...
jwt----介绍,原理
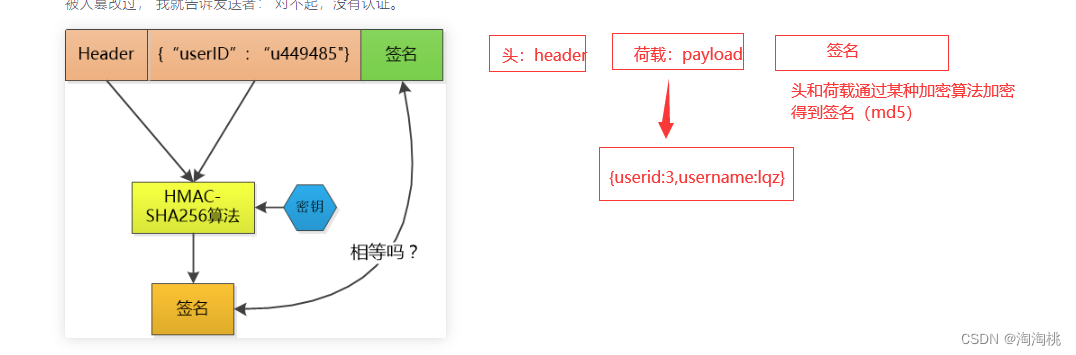
token:服务的生成的加密字符串,如果存在客户端浏览器上,就叫cookie -三部分:头,荷载,签名 -签发:登录成功,签发 -认证:认证类中认证 # jwt&…...

Three.js--》实现3d水晶小熊模型搭建
目录 项目搭建 初始化three.js基础代码 加载背景纹理 加载小熊模型 今天简单实现一个three.js的小Demo,加强自己对three知识的掌握与学习,只有在项目中才能灵活将所学知识运用起来,话不多说直接开始。 项目搭建 本案例还是借助框架书写…...

《阿里大数据之路》研读笔记(1)
首先先看到OLAP和OLTP的区别: OLTP(Online transaction processing):在线/联机事务处理。典型的OLTP类操作都比较简单,主要是对数据库中的数据进行增删改查,操作主体一般是产品的用户或者是操作人员。 OLAP(Online analytical processing):…...

Logback 日志框架详解
一、Logback 简介 Logback 是一个日志框架,旨在成为 log4j 的替代品。它由 Ceki Glc 创建并维护,是一款开源的日志框架,是 slf4j(Simple Logging Facade for Java)的实现。相比于 log4j,Logback 具有更高的…...

BIO、NIO、AIO 有什么区别?
BIO (Blocking I/O): Block IO 同步阻塞式 IO ,传统 IO,特点是模式简单、使用方便,并发处理能力低。 同步阻塞 I/O 模式,数据的读取写入必须阻塞在一个线程内等待其完成,在活动连接数不是特别高(…...

nginx和tomcat负载均衡、静态分离
tomcat重要目录 bin 存放启动和关闭Tomcat脚本conf存放Tomcat不同的配置文件doc存放Tomcat文档lib存放Tomcat运行需要的库文件logs存放Tomcat执行时的log文件src存放Tomcat的源代码webappsTomcat的主要Web发布目录work存放jsp编译后产生的class文件 nginx负载均衡原理 nginx实…...

用AI写出的高考作文!
今天是6月7日,又到了每一年高考的日子。小灰自己参加高考是在2004年,距离现在已经将近20年,现在回想起来,真的是恍如隔世。 今天高考语文的作文题是什么呢? 全国甲卷的题目是:人技术时间 人们因技术发展得以…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
