2023CCPC河南省赛 VP记录
感觉现在的xcpc,风格越来越像CF,不是很喜欢,还是更喜欢多点算法题的比赛
VP银了,VP银也是银
感觉省赛都是思维题,几乎没有算法题,感觉像打了场大型的CF
B题很简单没开出来,一直搞到最后,后来发现原来是卡常了....换种写法就过了
队名是偶像yinwuxx,杭电一队著名选手QwQ
话说好像很快就要篮球被了,我去,什么都不会了,一直在写CF的S b题
怎么办,感觉真的要没了
m d,别到时候区域赛名额没搞出来,篮球被没奖,直接亏损最大化了

Dashboard - 2023 CCPC Henan Provincial Collegiate Programming Contest - Codeforces
简略写一下思路吧:
A:
思路:签到,一开始还想字符串哈希判回文,结果只需要n^2判几次就好了
Code:队友写的
#include<bits/stdc++.h>
using namespace std;
const int mxv=2e5+9;
#define int long long
char s[mxv];
map<char,int> mp;
void solve(){cin>>s,mp.clear();int len=strlen(s)-1;if(len==0){cout<<"NaN\n";return;}int flag=1;for(int i=0;i<=len;i++){if(s[len]==s[i]){flag=1;for(int j=i,k=len;j<=k;j++,k--)if(s[j]!=s[k]){flag=0;break;}if(flag==1){cout<<"HE\n";return;}}if(mp[s[i]]==0) mp[s[i]]=1;else break;}cout<<"NaN\n";
}
signed main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t;cin>>t;while(t--) solve();return 0;
}B:

思路:
一开始的想法是二分K,然后在check函数里面把所有段的RMQ搞出来,如果存在这一段的最小值小于前一段的最大值就是False,否则就是True
然后T14了....因为线段树的RMQ复杂度多了个log....
然后就换了ST表,然后第二维开成33,MLE了....
事实上N是1e6的数据范围,开成22就够了
注意到不需要二分,直接枚举复杂度也是够的,于是换成了枚举
然后是莫名其妙的RE,到最后也是RE,也不知道为什么
事实上check函数里面不把RMQ扔进vector里面,直接扫一遍,记录上一次的最大值然后判就过了,被卡了好几小时....
Code:
#include <bits/stdc++.h>//#define int long longusing namespace std;const int mxn=1e6+10;
const int mxe=1e6+10;
const int mxv=1e3+10;
const int mod=1e9+7;int N;
int a[mxn];
int F_min[mxn][22],F_mx[mxn][22];
int lg[mxn];void ST_init(){for(int j=1;j<=22;j++){for(int i=1;i+(1<<(j-1))<=N;i++){F_min[i][j]=min(F_min[i][j-1],F_min[i+(1<<(j-1))][j-1]);F_mx[i][j]=max(F_mx[i][j-1],F_mx[i+(1<<(j-1))][j-1]);}}
}
void L_init(){lg[1]=0;for(int i=2;i<mxn;i++) lg[i]=lg[i>>1]+1;
}
int query_mi(int l,int r){int k=lg[r-l+1]; return min(F_min[l][k],F_min[r-(1<<k)+1][k]);
}
int query_mx(int l,int r){int k=lg[r-l+1]; return max(F_mx[l][k],F_mx[r-(1<<k)+1][k]);
}
void solve(){cin>>N;L_init();for(int i=1;i<=N;i++){cin>>a[i];F_min[i][0]=F_mx[i][0]=a[i];}if(is_sorted(a+1,a+1+N)){cout<<N<<'\n';return;}ST_init();int ans=0;for(int k=1;k<=N;k++){int last=0,ok=1;for(int l=1;l<=N;l+=k){int r=min(l+k-1,N);if(query_mi(l,r)<last){ok=0;break;}last=query_mx(l,r);}ans+=ok;}cout<<ans<<'\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;while(__--)solve();return 0;
}C:

思路:
猜了个结论就过了,很奇怪,这种题还是第一次碰到
#include <bits/stdc++.h>//#define int long longusing namespace std;const int mxn=1e6+10;
const int mxe=1e6+10;
const int mxv=1e3+10;
const int mod=1e9+7;string s1;void solve(){cin>>s1;string s2=s1.substr(0,1000);s1.erase(0,1000);if(s1.find(s2)!=-1) cout<<"No"<<'\n';else cout<<"Yes"<<'\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;while(__--)solve();return 0;
}
D题图论难题,会不了一点
E:

思路:
一开始队友写的DFS,然后T了,换成DP然后MLE了
是个很篮球杯风格的DP,但是开了三维MLE
换成vector也MLE,关掉define也是MLE
这件事告诉我们,正式比赛一般是不卡这种东西的
我滚了一下数组就AC了
Code:
#include<bits/stdc++.h>
using namespace std;
const int mxv=5e2+9,mxn=1e3+3;
const int Inf=0x3f3f3f3f;
//#define int long long
int n,m,x;
char s[mxv][mxv];
int dx[]={0,0,1};
int dy[]={0,1,0};
int dp[2][mxv][mxn];
void solve(){cin>>n>>m>>x;// vector< vector < vector<int> > > dp(2,vector< vector<int> >(m+1,vector<int>(x+1,-Inf)));//dp(i,j,k):到达(i,j),已经修改了k次的最大价值for(int i=0;i<=1;i++){for(int j=0;j<=m;j++){for(int k=0;k<=x;k++){dp[i][j][k]=-Inf;}}}for(int i=1;i<=n;i++) cin>>s[i]+1;if(s[1][1]=='1') dp[1&1][1][0]=1;else if(s[1][1]=='0') dp[1&1][1][0]=0;else dp[1][1][1]=1,dp[1&1][1][0]=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){for(int k=0;k<=x;k++){if(i+1<=n){dp[(i+1)&1][j][k]=max(dp[(i+1)&1][j][k],dp[i&1][j][k]);if(s[i+1][j]=='1')dp[(i+1)&1][j][k]=max(dp[i&1][j][k]+1,dp[(i+1)&1][j][k]); if(s[i+1][j]=='?'&&k-1>=0)dp[(i+1)&1][j][k]=max(dp[i&1][j][k-1]+1,dp[(i+1)&1][j][k]);}if(j+1<=m){dp[i&1][j+1][k]=max(dp[i&1][j+1][k],dp[i&1][j][k]);if(s[i][j+1]=='1')dp[i&1][j+1][k]=max(dp[i&1][j][k]+1,dp[i&1][j+1][k]); if(s[i][j+1]=='?'&&k-1>=0)dp[i&1][j+1][k]=max(dp[i&1][j][k-1]+1,dp[i&1][j+1][k]);}}}}int ans=0;for(int i=0;i<=x;i++) ans=max(ans,dp[n&1][m][i]);cout<<ans<<"\n";
}
signed main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--) solve();return 0;
}F:

思路:
首先显然是要排序,然后选K个元素对应区间长度为K,所以就是滑动窗口滑过去就可以了,维护一下RMQ,统计一下最大的min*max
Code:
#include <bits/stdc++.h>#define int long longusing namespace std;const int mxn=5e5+10;
const int mxe=5e5+10;
const int mxv=1e3+10;
const int mod=1e9+7;struct ty{int mi;
}tree[mxe<<2];int N,K;
int a[mxn],b[mxn];void pushup(int rt){tree[rt].mi=min(tree[rt<<1].mi,tree[rt<<1|1].mi);
}
int query(int rt,int l,int r,int x,int y){if(x<=l&&r<=y){return tree[rt].mi;}int mid=l+r>>1;int res=1e18;if(x<=mid) res=min(res,query(rt<<1,l,mid,x,y));if(y>mid) res=min(res,query(rt<<1|1,mid+1,r,x,y));return res;
}
void build(int rt,int l,int r){if(l==r){tree[rt].mi=b[l];return;}int mid=l+r>>1;build(rt<<1,l,mid);build(rt<<1|1,mid+1,r);pushup(rt);
}
void solve(){cin>>N>>K;for(int i=1;i<=N;i++) cin>>a[i];sort(a+1,a+1+N);for(int i=1;i<=N;i++) b[i]=a[i]-a[i-1];build(1,2,N);//for(int i=1;i<=N;i++) cout<<a[i]<<" \n"[i==N];//for(int i=2;i<=N;i++) cout<<b[i]<<" \n"[i==N];int ans=1e18;for(int l=1;l+K-1<=N;l++){int r=l+K-1;int mx=a[r]-a[l];int mi=query(1,2,N,l+1,r);ans=min(ans,mi*mx);}cout<<ans<<'\n';
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int __=1;//cin>>__;while(__--)solve();return 0;
}
G题大模拟不想写
H:

思路:
需要对N和2*k进行分类讨论
如果N/k<0.5,那么最小值一定是0,最大值就是0.5,0.5.....这样子放,答案就是N/0.5,因为最后几个一定是0
否则最小值就是0.49,0.49这样子放,答案就是最后剩下的数的上取整,最大值就是0.5,0.5这样放,答案就是K-1个1+最后一个数上取整
Code:
#include<bits/stdc++.h>
//#define int long long
#define rep(i,a,n) for(int i=a; i<=n ;i++)
#define pii pair<int,int>
#define pb push_back
#define fi first
#define sc second
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
const double eps=0.5, exs=0.49999999999999999;
void solve(){int n, k;cin>>n>>k;double c=n-(k-1)*exs;//cout<<c<<'\n';if(c<0.5){int ans2=int(n/0.5);cout<<0<<' '<<ans2<<'\n';}else{int ans1=0, ans2=0;ans1=int(c+0.5);double d=n-(k-1)*0.5;ans2=int(d+0.5)+k-1;cout<<ans1<<' '<<ans2<<'\n';}
}
signed main(){ios;int t=1;cin>>t;while(t--){solve();}return 0;
}I:

直接看这个:【容斥+扫描线】2023CCPC河南省赛 I 数正方形_lamentropetion的博客-CSDN博客
JL都是神秘题,不会QwQ
相关文章:

2023CCPC河南省赛 VP记录
感觉现在的xcpc,风格越来越像CF,不是很喜欢,还是更喜欢多点算法题的比赛 VP银了,VP银也是银 感觉省赛都是思维题,几乎没有算法题,感觉像打了场大型的CF B题很简单没开出来,一直搞到最后&…...
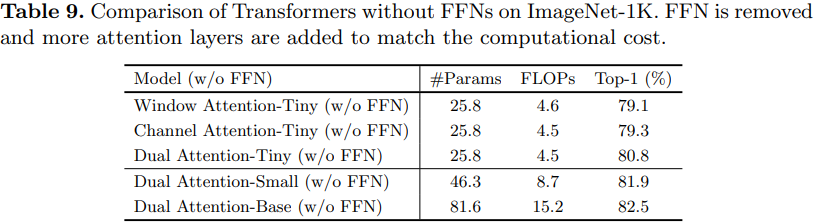
【ECCV2022】DaViT: Dual Attention Vision Transformers
DaViT: Dual Attention Vision Transformers, ECCV2022 解读:【ECCV2022】DaViT: Dual Attention Vision Transformers - 高峰OUC - 博客园 (cnblogs.com) DaViT:双注意力Vision Transformer - 知乎 (zhihu.com) DaViT: Dual Attention Vision Trans…...

Apache 配置与应用
Apache 配置与应用 一、构建虚拟 Web 主机httpd服务支持的虚拟主机类型包括以下三种: 二、基于域名的虚拟主机1.为虚拟主机提供域名解析方法一:部署DNS域名解析服务器 来提供域名解析方法二:在/etc/hosts 文件中临时配置域名与IP地址的映射关…...
OpenGL 纹理
1.简介 纹理是一个2D图片(甚至也有1D和3D的纹理),它可以用来添加物体的细节;你可以想象纹理是一张绘有砖块的纸,无缝折叠贴合到你的3D的房子上,这样你的房子看起来就像有砖墙外表了。 为了能够把纹理映射(M…...

Jeston Orin Nnao 安装pytorch与torchvision环境
大家好,我是虎哥,Jeston Orin nano 8G模块,提供高达 40 TOPS 的 AI 算力,安装好了Jetpack5.1之后,我们需要配置一些支持环境,来为我们后续的深度学习开发提供支持。本章内容,我将主要围绕安装对…...

ROS:常用可视化工具的使用
目录 一、日志输出工具——rqt_console二、绘制数据曲线——rqt_plot三、图像渲染工具——rqt_image_view四、图形界面总接口——rqt五、Rviz六、Gazebo 一、日志输出工具——rqt_console 启动海龟键盘控制节点,打开日志输出工具 roscorerosrun turtlesim turtles…...
智能应用搭建平台——LCHub低代码表单 vs 流程表单 vs 仪表盘
1. LCHub低代码如何选择 「流程表单」:填报数据,并带有流程审批功能,适合报销、请假申请或其他工作流; 「表单」:填报数据,并带有数据协作功能,如修改、删除、导入、导出,并可以给不同的人不同的管理权限; 「仪表盘」:数据分析处理、结果展示功能,如数据汇总、趋…...
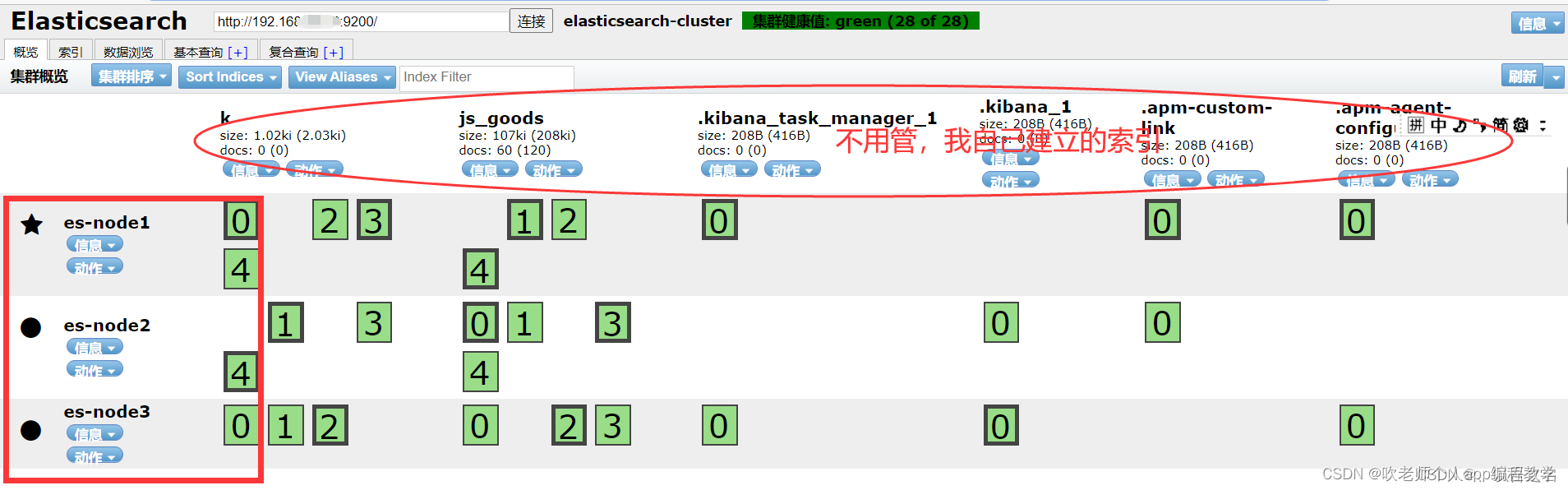
Mac下通过Docker安装ElasticSearch集群
1、安装ElasticSearch 使用docker直接获取es镜像,执行命令docker pull elasticsearch:7.7.0 执行完成后,执行docker images即可看到上一步拉取的镜像。 2、创建数据挂在目录,以及配置ElasticSearch集群配置文件 创建数据文件挂载目录 mkdir -…...

MySQL redo log、undo log、binlog
MySQL是一个广泛使用的关系型数据库管理系统,它通过一系列的日志来保证数据的一致性和持久性。在MySQL中,有三个重要的日志组件,它们分别是redo log(重做日志)、undo log(回滚日志)和binlog&…...

文件包含漏洞
一、原理解析。 开发人员通常会把可重复使用的函数写到单个文件中,在使用到某些函数时,可直接调用此文件,而无须再次编写,这种调用文件的过程被称为包含。 注意:对于开发人员来讲,文件包含很有用…...

Python 中的 F-Test
文章目录 F 统计量和 P 值方差(ANOVA) 分析中的 F 值 本篇文章介绍 F 统计、F 分布以及如何使用 Python 对数据执行 F-Test 测试。 F 统计量是在方差分析检验或回归分析后获得的数字,以确定两个总体的平均值是否存在显着差异。 它类似于 T 检验的 T 统计量…...

Docker网络模式
一、docker网络概述 1、docker网络实现的原理 Docker使用Linux桥接,在宿主机虚拟一个Docker容器网桥(docker0),Docker启动一个容器时会根据Docker网桥的网段分配给容器一个IP地址,称为Container-IP, 同时Docker网桥是 每个容器的…...

百度离线资源治理
作者 | 百度MEG离线优化团队 导读 近些年移动互联网的高速发展驱动了数据爆发式的增长,各大公司之间都在通过竞争获得更大的增长空间,大数据计算的效果直接影响到公司的发展,而这背后其实依赖庞大的算力及数据作为支撑,因此在满足…...
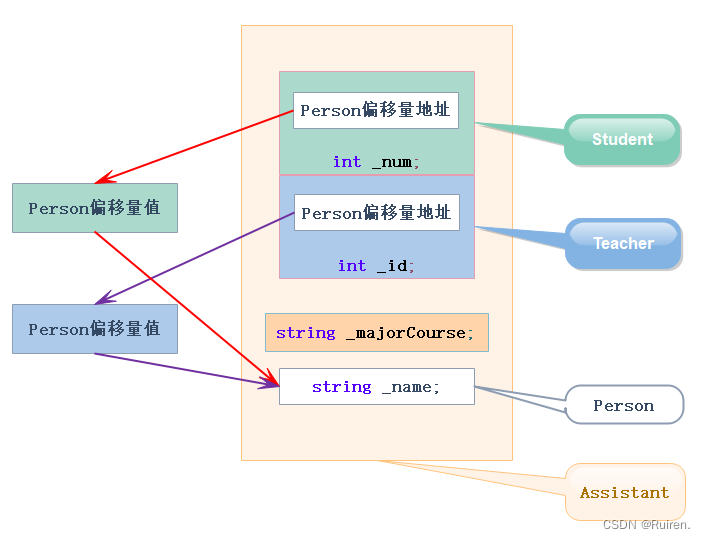
C++进阶之继承
文章目录 前言一、继承的概念及定义1.继承概念2.继承格式与访问限定符3.继承基类与派生类的访问关系变化4.总结 二、基类和派生类对象赋值转换基本概念与规则 三、继承中的作用域四、派生类的默认成员函数五、继承与友元六、继承与静态成员六、复杂的菱形继承及菱形虚拟继承七、…...
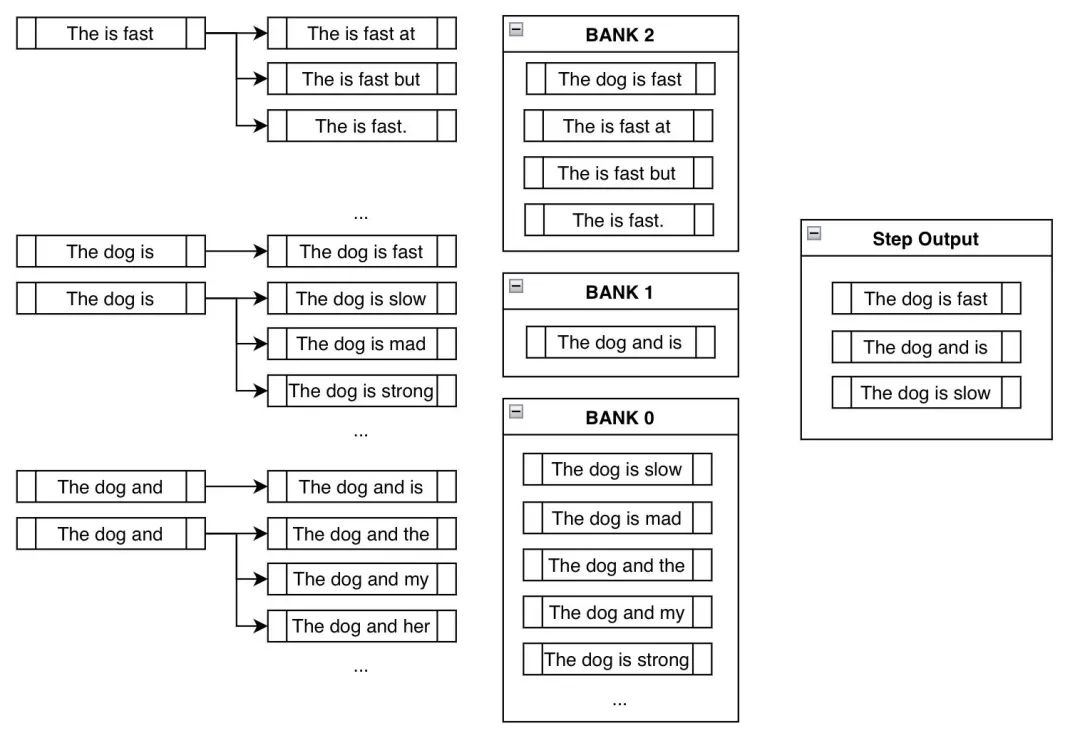
在 Transformers 中使用约束波束搜索引导文本生成
引言 本文假设读者已经熟悉文本生成领域波束搜索相关的背景知识,具体可参见博文 如何生成文本: 通过 Transformers 用不同的解码方法生成文本。 与普通的波束搜索不同,约束 波束搜索允许我们控制所生成的文本。这很有用,因为有时我们确切地知…...

Centos7更换OpenSSL版本
OpenSSL 1.1.0 用户应升级至 1.1.0aOpenSSL 1.0.2 用户应升级至 1.0.2iOpenSSL 1.0.1 用户应升级至 1.0.1u 查看openssl版本 openssl version -v选择升级版本 我的版本是OpenSSL 1.0.2系列,所以要升级1.0.2i https://www.openssl.org/source/old/1.0.2/openssl-…...
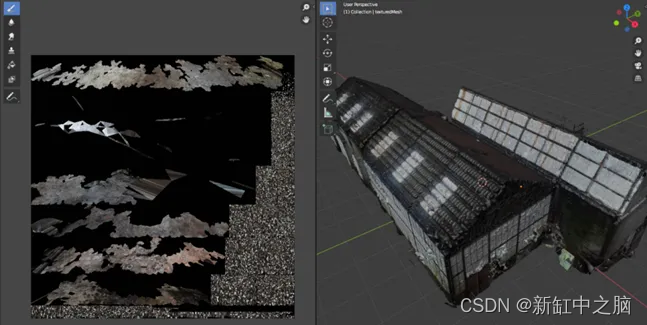
基于摄影测量的三维重建【终极指南】
我们生活的时代非常令人兴奋,如果你对 3D 东西感兴趣,更是如此。 我们有能力使用任何相机,从感兴趣的物体中捕捉一些图像数据,并在眨眼间将它们变成 3D 资产! 这种通过简单的数据采集阶段进行的 3D 重建过程是许多行业…...

配置ThreadPoolExecutor
ThreadPoolExecutor为一些Executor 提供了基本的实现,这些Executor 是由Executors中的newCachedThreadPool、newFixedThreadPool和newScheduledThreadExecutor 等工厂方法返回的。ThreadPoolExecutor是一个灵活的、稳定的线程池,允许进行各种定制。 如果默认的执行策略不能满足…...
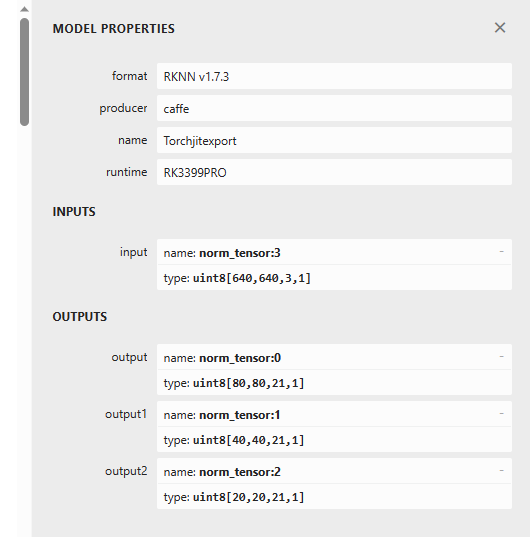
Yolov5s算法从训练到部署
文章目录 PyTorch GPU环境搭建查看显卡CUDA版本Anaconda安装PyTorch环境安装PyCharm中验证 训练算法模型克隆Yolov5代码工程制作数据集划分训练集、验证集修改工程相关文件配置预训练权重文件配置数据文件配置模型文件配置 超参数配置 测试训练出来的算法模型 量化转换算法模型…...
分布式补充技术 01.AOP技术
01.AOP技术是对于面向对象编程(OOP)的补充。是按照OCP原则进行的编写,(ocp是修改模块权限不行,扩充可以) 02.写一个例子: 创建一个新的java项目,在main主启动类中,写如下代码。 package com.co…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...
LINUX编译vlc
下载 VideoLAN / VLC GitLab 选择最新的发布版本 准备 sudo apt install -y xcb bison sudo apt install -y autopoint sudo apt install -y autoconf automake libtool编译ffmpeg LINUX FFMPEG编译汇总(最简化)_底部的附件列表中】: ffmpeg - lzip…...
