(转载)基于模拟退火算法的TSP问题求解(matlab实现)
1 理论基础
1.1 模拟退火算法基本原理


1.2 TSP问题介绍
2 案例背景
2.1 问题描述

2.2 解题思路及步骤
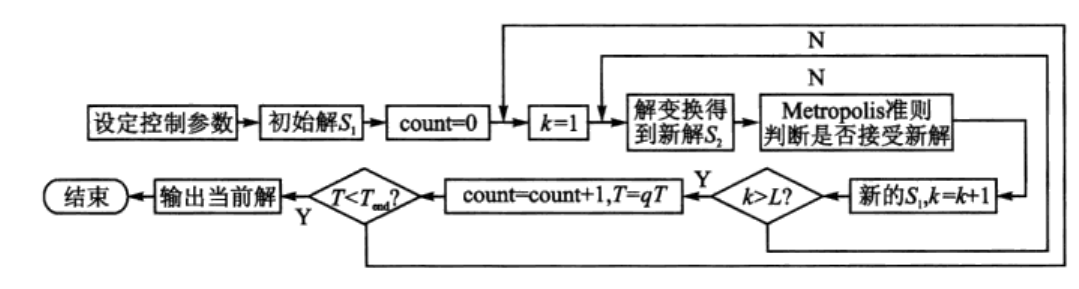


3 MATLAB程序实现
3.1 计算距离矩阵
function D=Distanse(a)
%% 计算两两城市之间的距离
%输入 a 各城市的位置坐标
%输出 D 两两城市之间的距离
row=size(a,1);
D=zeros(row,row);
for i=1:rowfor j=i+1:rowD(i,j)=((a(i,1)-a(j,1))^2+(a(i,2)-a(j,2))^2)^0.5;D(j,i)=D(i,j);end
end
3.2 画路线轨迹图
function DrawPath(Chrom,X)
%% 画路径函数
%输入
% Chrom 待画路径
% X 各城市坐标位置
R=[Chrom(1,:) Chrom(1,1)]; %一个随机解(个体)
figure;
hold on
plot(X(:,1),X(:,2),'o','color',[0.5,0.5,0.5])
plot(X(Chrom(1,1),1),X(Chrom(1,1),2),'rv','MarkerSize',20)
for i=1:size(X,1)text(X(i,1)+0.05,X(i,2)+0.05,num2str(i),'color',[1,0,0]);
end
A=X(R,:);
row=size(A,1);
for i=2:row[arrowx,arrowy] = dsxy2figxy(gca,A(i-1:i,1),A(i-1:i,2));%坐标转换annotation('textarrow',arrowx,arrowy,'HeadWidth',8,'color',[0,0,1]);
end
hold off
xlabel('横坐标')
ylabel('纵坐标')
title('轨迹图')
box on3.3 输出路径函数
function p=OutputPath(R)
%% 输出路径函数
%输入:R 路径
R=[R,R(1)];
N=length(R);
p=num2str(R(1));
for i=2:Np=[p,'—>',num2str(R(i))];
end
disp(p)3.4 可行解路线长度函数
function len=PathLength(D,Chrom)
%% 计算各个体的路径长度
% 输入:
% D 两两城市之间的距离
% Chrom 个体的轨迹
[row,col]=size(D);
NIND=size(Chrom,1);
len=zeros(NIND,1);
for i=1:NINDp=[Chrom(i,:) Chrom(i,1)];i1=p(1:end-1);i2=p(2:end);len(i,1)=sum(D((i1-1)*col+i2));
end
3.5 生成新解
function S2=NewAnswer(S1)
%% 输入
% S1:当前解
%% 输出
% S2:新解
N=length(S1);
S2=S1;
a=round(rand(1,2)*(N-1)+1); %产生两个随机位置 用来交换
W=S2(a(1));
S2(a(1))=S2(a(2));
S2(a(2))=W; %得到一个新路线3.6Metropolis准则函数
function [S,R]=Metropolis(S1,S2,D,T)
%% 输入
% S1: 当前解
% S2: 新解
% D: 距离矩阵(两两城市的之间的距离)
% T: 当前温度
%% 输出
% S: 下一个当前解
% R: 下一个当前解的路线距离
%%
R1=PathLength(D,S1); %计算路线长度
N=length(S1); %得到城市的个数R2=PathLength(D,S2); %计算路线长度
dC=R2-R1; %计算能力之差
if dC<0 %如果能力降低 接受新路线S=S2;R=R2;
elseif exp(-dC/T)>=rand %以exp(-dC/T)概率接受新路线S=S2;R=R2;
else %不接受新路线S=S1;R=R1;
end3.7 主函数

主函数代码如下:
clc;
clear;
close all;
%%
tic
T0=1000; % 初始温度
Tend=1e-3; % 终止温度
L=500; % 各温度下的迭代次数(链长)
q=0.9; %降温速率%% 加载数据
load CityPosition1;
%%
D=Distanse(X); %计算距离矩阵
N=size(D,1); %城市的个数
%% 初始解
S1=randperm(N); %随机产生一个初始路线%% 画出随机解的路径图
DrawPath(S1,X)
pause(0.0001)
%% 输出随机解的路径和总距离
disp('初始种群中的一个随机值:')
OutputPath(S1);
Rlength=PathLength(D,S1);
disp(['总距离:',num2str(Rlength)]);%% 计算迭代的次数Time
Time=ceil(double(solve(['1000*(0.9)^x=',num2str(Tend)])));
count=0; %迭代计数
Obj=zeros(Time,1); %目标值矩阵初始化
track=zeros(Time,N); %每代的最优路线矩阵初始化
%% 迭代
while T0>Tendcount=count+1; %更新迭代次数temp=zeros(L,N+1);for k=1:L%% 产生新解S2=NewAnswer(S1);%% Metropolis法则判断是否接受新解[S1,R]=Metropolis(S1,S2,D,T0); %Metropolis 抽样算法temp(k,:)=[S1 R]; %记录下一路线的及其路程end%% 记录每次迭代过程的最优路线[d0,index]=min(temp(:,end)); %找出当前温度下最优路线if count==1 || d0<Obj(count-1)Obj(count)=d0; %如果当前温度下最优路程小于上一路程则记录当前路程elseObj(count)=Obj(count-1);%如果当前温度下最优路程大于上一路程则记录上一路程endtrack(count,:)=temp(index,1:end-1); %记录当前温度的最优路线T0=q*T0; %降温fprintf(1,'%d\n',count) %输出当前迭代次数
end
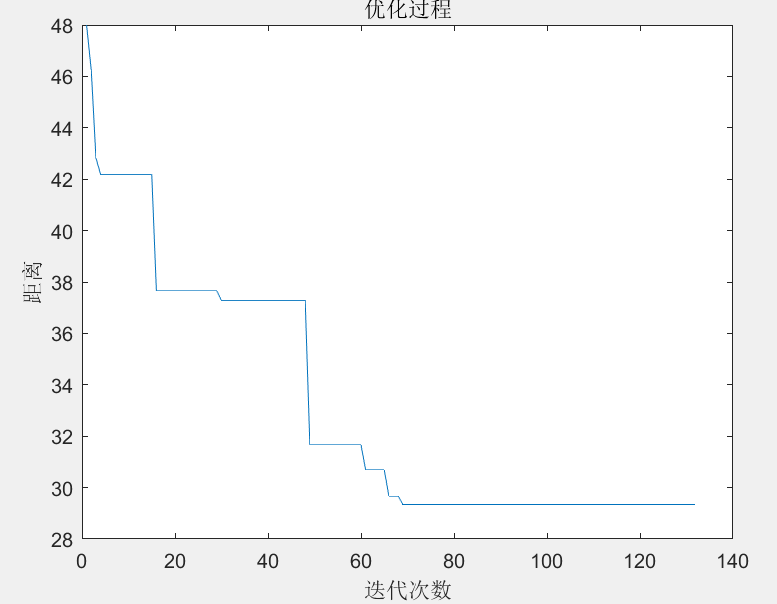
%% 优化过程迭代图
figure
plot(1:count,Obj)
xlabel('迭代次数')
ylabel('距离')
title('优化过程')%% 最优解的路径图
DrawPath(track(end,:),X)%% 输出最优解的路线和总距离
disp('最优解:')
S=track(end,:);
p=OutputPath(S);
disp(['总距离:',num2str(PathLength(D,S))]);
disp('-------------------------------------------------------------')
toc4 结果分析


最优解为:
9—>11—>1—>8—>13—>7—>12—>6—>5—>4—>3—>14—>2—>10—>9
总距离:29.6889
X=rand(N,2)*10;
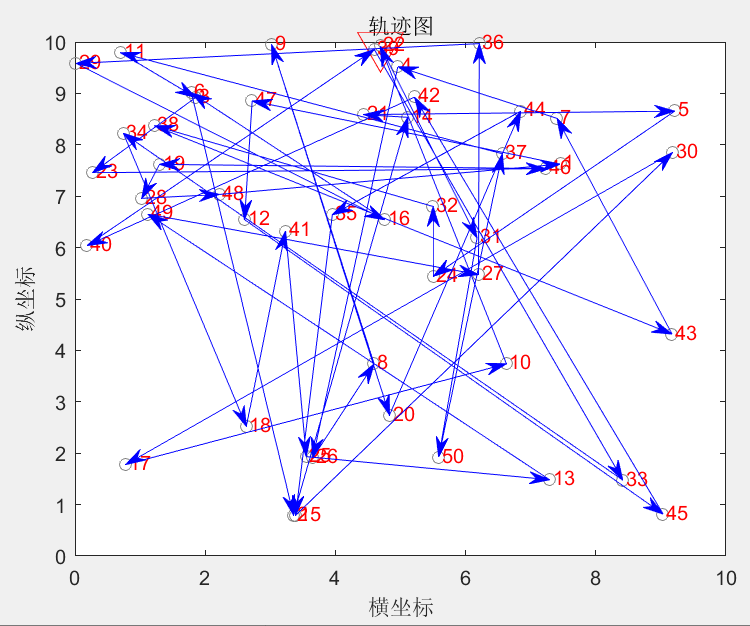
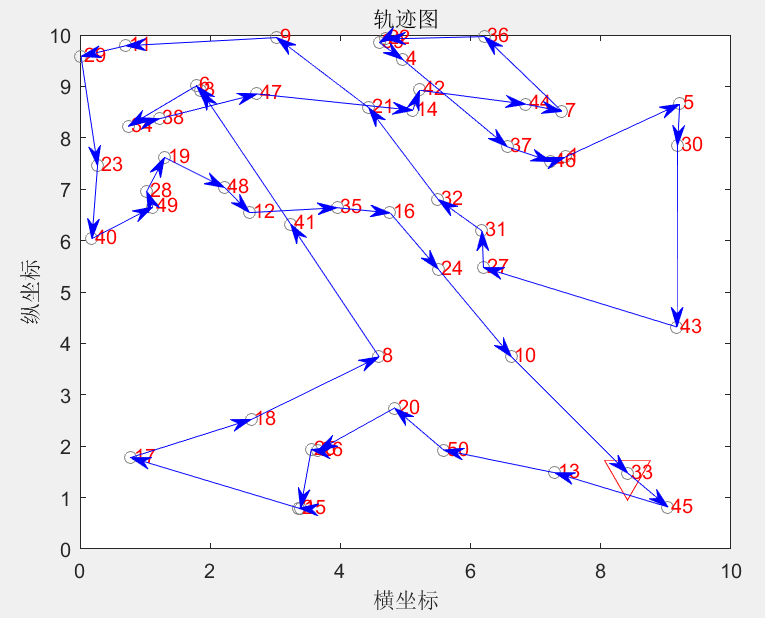
即可得到如下结果:优化前的轨迹如图5所示,优化后的轨迹如图6所示,优化迭代过程如图7所示。
初始种群中的个随机解:
22—>31—>50—>37—>11—>3—>23—>46—>19—>28—>48—>1—>47—>12—>45—>42—>40—>39—>33—>34—>18—>41—>25—>13—>49—>27—>36—>29—>16—>6—>2—>14—>21—>5—>24—>32—>38—>43—>7—>4—>26—>8—>9—>20—>44—>35—>15—>30—>17—>10—>22
总距离:271.7719
最优解:
33—>45—>13—>50—>20—>26—>25—>15—>2—>17—>18—>8—>41—>3—>6—>34—>38—>47—>14—>42—>44—>7—>36—>22—>39—>4—>37—>46—>1—>5—>30—>43—>27—>31—>32—>21—>9—>11—>29—>23—>40—>49—>28—>19—>48—>12—>35—>16—>24—>10—>33
总距离:71.3071

5 延伸阅读
5.1 模拟退火算法的改进
5.2 算法的局限性
相关文章:

(转载)基于模拟退火算法的TSP问题求解(matlab实现)
1 理论基础 1.1 模拟退火算法基本原理 模拟退火(simulated annealing,SA)算法的思想最早是由Metropolis等提出的。其出发点是基于物理中固体物质的退火过程与一般的组合优化问题之间的相似性。模拟退火法是一种通用的优化算法,其物理退火过程由以下三部分组成&am…...

splitpcap 使用说明
背景 当PCAP原始文件特别巨大的时候,整个文件直接载入内存是相当耗时的,于是一个简单的想法是将大的PCAP切分成若干小PCAP。对于这个任务,现有工具splitcap是可以完成的。无论是按照主机对、还是按照五元组信息切分,splitcap都会…...

配置docker阿里云镜像加速
默认情况下docker安装镜像文件是从docker官方的镜像中心下载:https://hub.docker.com/ , 有时速度慢,可以通过配置docker阿里云镜像来加速,配置后,就从国内阿里云下载。 注册阿里云用户,登录->工作台-&g…...
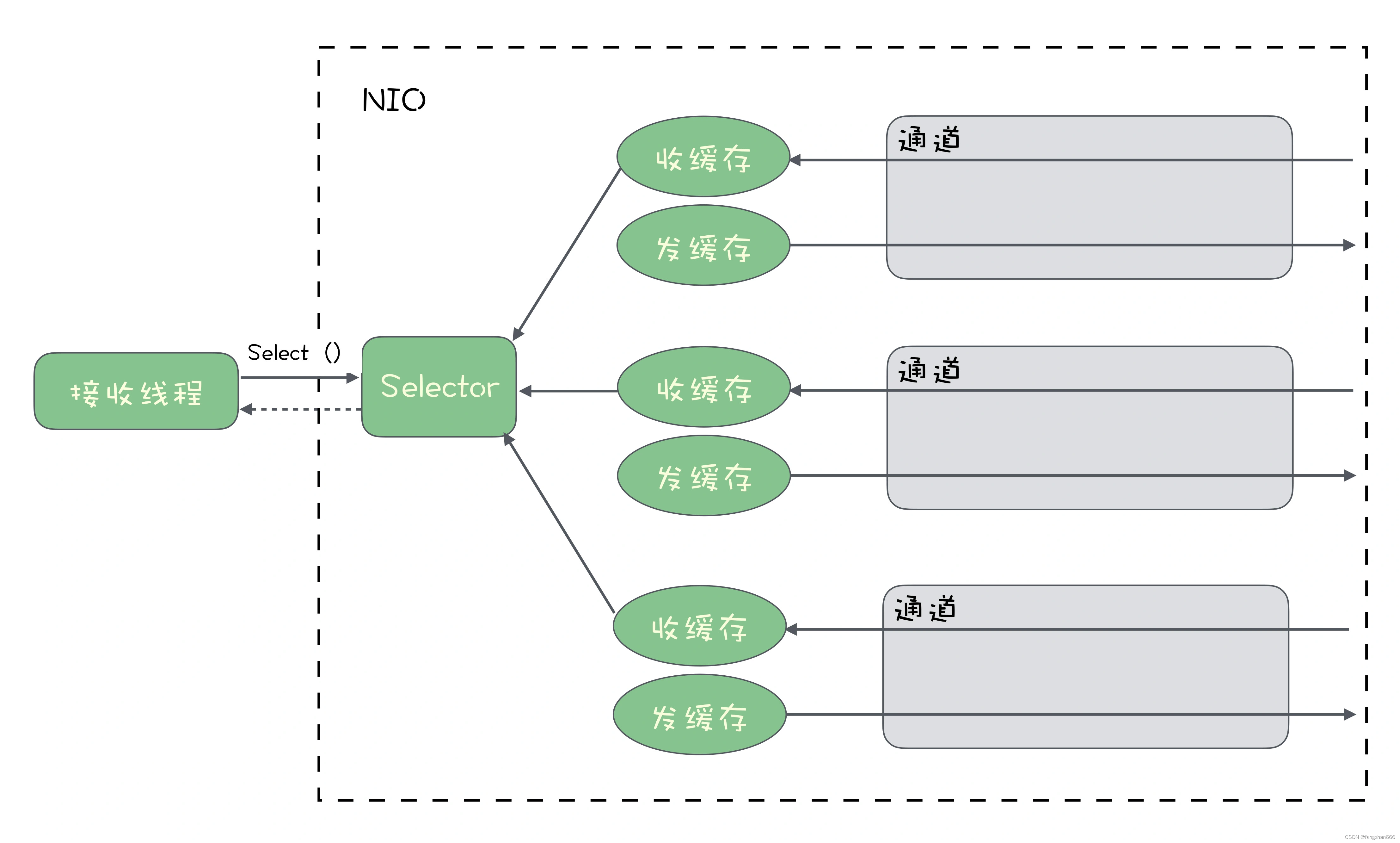
《消息队列高手课》课程学习笔记(八)
如何实现高性能的异步网络传输? **异步与同步模型最大的区别是,同步模型会阻塞线程等待资源,而异步模型不会阻塞线程,它是等资源准备好后,再通知业务代码来完成后续的资源处理逻辑。**这种异步设计的方法,…...

DC电源模块在工业自动化的应用
BOSHIDA DC电源模块在工业自动化的应用 随着自动化技术的不断发展,DC电源模块已成为工业控制系统中不可或缺的一个组成部分。在许多自动化系统中,如机器人、控制器、PLC等,都需要使用到直流电源模块来提供稳定可靠的电源,以确保系…...

Java容器-集合
目录 1.Java容器概述 2.集合框架 3.Collection接口中的方法使用 4.iterator() 5.List接口 2.ArrayList、LinkedList、Vector相同点 3.不同点 1.ArrayList 2.LinkedList 3.Vector 4.Vector源码分析 5.ArrayList源码分析 6.LinkedList源码分析 6.List中的常用方法 …...
总结890
学习目标: 月目标:6月(线性代数强化9讲2遍,背诵15篇短文,考研核心词过三遍) 周目标:线性代数强化3讲,英语背3篇文章并回诵,检测 每日必复习(5分钟ÿ…...

2023年5月青少年机器人技术等级考试理论综合试卷(二级)
青少年机器人技术等级考试理论综合试卷(二级)2023.6 分数: 100 题数: 45 一、 单选题(共 30 题, 共 60 分) 1.下图中的凸轮机构使用了摆动型从动件的是? ( ) A.a B.b C.c D.d 试题类…...

2023CCPC河南省赛 VP记录
感觉现在的xcpc,风格越来越像CF,不是很喜欢,还是更喜欢多点算法题的比赛 VP银了,VP银也是银 感觉省赛都是思维题,几乎没有算法题,感觉像打了场大型的CF B题很简单没开出来,一直搞到最后&…...
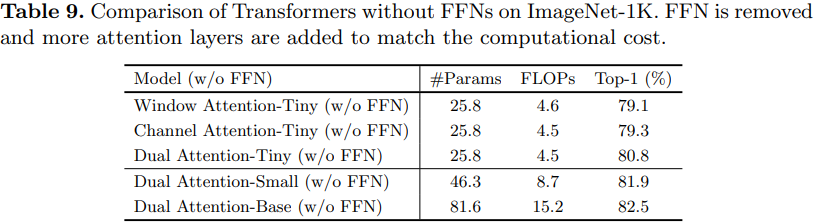
【ECCV2022】DaViT: Dual Attention Vision Transformers
DaViT: Dual Attention Vision Transformers, ECCV2022 解读:【ECCV2022】DaViT: Dual Attention Vision Transformers - 高峰OUC - 博客园 (cnblogs.com) DaViT:双注意力Vision Transformer - 知乎 (zhihu.com) DaViT: Dual Attention Vision Trans…...

Apache 配置与应用
Apache 配置与应用 一、构建虚拟 Web 主机httpd服务支持的虚拟主机类型包括以下三种: 二、基于域名的虚拟主机1.为虚拟主机提供域名解析方法一:部署DNS域名解析服务器 来提供域名解析方法二:在/etc/hosts 文件中临时配置域名与IP地址的映射关…...
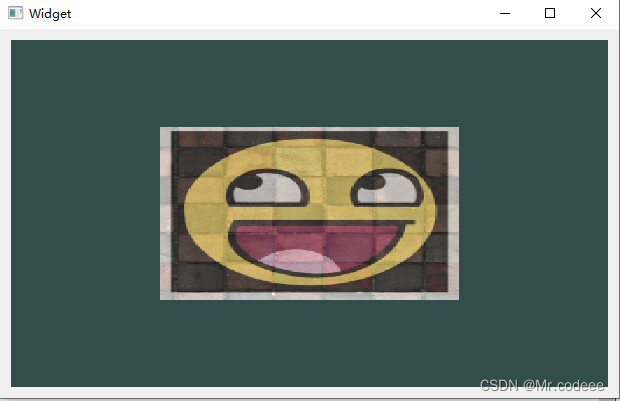
OpenGL 纹理
1.简介 纹理是一个2D图片(甚至也有1D和3D的纹理),它可以用来添加物体的细节;你可以想象纹理是一张绘有砖块的纸,无缝折叠贴合到你的3D的房子上,这样你的房子看起来就像有砖墙外表了。 为了能够把纹理映射(M…...

Jeston Orin Nnao 安装pytorch与torchvision环境
大家好,我是虎哥,Jeston Orin nano 8G模块,提供高达 40 TOPS 的 AI 算力,安装好了Jetpack5.1之后,我们需要配置一些支持环境,来为我们后续的深度学习开发提供支持。本章内容,我将主要围绕安装对…...

ROS:常用可视化工具的使用
目录 一、日志输出工具——rqt_console二、绘制数据曲线——rqt_plot三、图像渲染工具——rqt_image_view四、图形界面总接口——rqt五、Rviz六、Gazebo 一、日志输出工具——rqt_console 启动海龟键盘控制节点,打开日志输出工具 roscorerosrun turtlesim turtles…...
智能应用搭建平台——LCHub低代码表单 vs 流程表单 vs 仪表盘
1. LCHub低代码如何选择 「流程表单」:填报数据,并带有流程审批功能,适合报销、请假申请或其他工作流; 「表单」:填报数据,并带有数据协作功能,如修改、删除、导入、导出,并可以给不同的人不同的管理权限; 「仪表盘」:数据分析处理、结果展示功能,如数据汇总、趋…...
Mac下通过Docker安装ElasticSearch集群
1、安装ElasticSearch 使用docker直接获取es镜像,执行命令docker pull elasticsearch:7.7.0 执行完成后,执行docker images即可看到上一步拉取的镜像。 2、创建数据挂在目录,以及配置ElasticSearch集群配置文件 创建数据文件挂载目录 mkdir -…...

MySQL redo log、undo log、binlog
MySQL是一个广泛使用的关系型数据库管理系统,它通过一系列的日志来保证数据的一致性和持久性。在MySQL中,有三个重要的日志组件,它们分别是redo log(重做日志)、undo log(回滚日志)和binlog&…...

文件包含漏洞
一、原理解析。 开发人员通常会把可重复使用的函数写到单个文件中,在使用到某些函数时,可直接调用此文件,而无须再次编写,这种调用文件的过程被称为包含。 注意:对于开发人员来讲,文件包含很有用…...

Python 中的 F-Test
文章目录 F 统计量和 P 值方差(ANOVA) 分析中的 F 值 本篇文章介绍 F 统计、F 分布以及如何使用 Python 对数据执行 F-Test 测试。 F 统计量是在方差分析检验或回归分析后获得的数字,以确定两个总体的平均值是否存在显着差异。 它类似于 T 检验的 T 统计量…...

Docker网络模式
一、docker网络概述 1、docker网络实现的原理 Docker使用Linux桥接,在宿主机虚拟一个Docker容器网桥(docker0),Docker启动一个容器时会根据Docker网桥的网段分配给容器一个IP地址,称为Container-IP, 同时Docker网桥是 每个容器的…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
