softmax 函数
https://blog.csdn.net/m0_37769093/article/details/107732606
softmax 函数如下所示:
y i = exp ( x i ) ∑ j = 1 n exp ( x j ) y_{i} = \frac{\exp(x_{i})}{\sum_{j=1}^{n}{\exp(x_j)}} yi=∑j=1nexp(xj)exp(xi)
softmax求导如下:
i = j i = j i=j 的情况:
∂ y i ∂ x i = exp ( x i ) ∑ j = 1 n exp ( x j ) − ( exp ( x i ) ) 2 ( ∑ j = 1 n exp ( x j ) ) 2 \frac{\partial y_{i}}{\partial x_{i}} = \frac{\exp(x_{i})}{\sum_{j=1}^{n}{\exp(x_j)}} - \frac{(\exp(x_{i}))^2}{(\sum_{j=1}^{n}{\exp(x_j)})^2} ∂xi∂yi=∑j=1nexp(xj)exp(xi)−(∑j=1nexp(xj))2(exp(xi))2
∂ y i ∂ x i = y i − ( y i ) 2 \frac{\partial y_{i}}{\partial x_{i}} = y_{i} - (y_{i})^2 ∂xi∂yi=yi−(yi)2
i ≠ j i \neq j i=j 的情况:
∂ y i ∂ x j = − ( exp ( x i ) × exp ( x j ) ) ( ∑ j = 1 n exp ( x j ) ) 2 \frac{\partial y_{i}}{\partial x_{j}} = - \frac{(\exp(x_{i})\times\exp(x_{j}))}{(\sum_{j=1}^{n}{\exp(x_j)})^2} ∂xj∂yi=−(∑j=1nexp(xj))2(exp(xi)×exp(xj))
∂ y i ∂ x j = − y i y j \frac{\partial y_{i}}{\partial x_{j}} = - y_{i}y_{j} ∂xj∂yi=−yiyj
相关文章:

softmax 函数
https://blog.csdn.net/m0_37769093/article/details/107732606 softmax 函数如下所示: y i exp ( x i ) ∑ j 1 n exp ( x j ) y_{i} \frac{\exp(x_{i})}{\sum_{j1}^{n}{\exp(x_j)}} yi∑j1nexp(xj)exp(xi) softmax求导如下: i j…...

【SpringMVC】拦截器和过滤器之间的区别
过滤器 拦截器 调用机制 基于函数的回调 基于反射机制(动态代理) 依赖关系 依赖Servlet容器 不依赖Servlet容器 作用范围 对几乎所有的请求起作用 只对action请求起作用 访问范围 不能访问action上下文、栈 可以访问action上下文、栈 action生命周期 中的调用次数…...
springboot第25集:实体类定义规则
PO:持久化对象,一个PO对象对应一张表里面的一条记录。全部对应 VO:View视图对象,用来在页面中展示数据的,页面需要哪些字段属性就添加哪些,查询出来之后赋值操作比PO对象要简单。所以提高性能。 DTO&#x…...

【python】—— python的基本介绍并附安装教程
前言: 今天,我将给大家讲解关于python的基本知识,让大家对其有个基本的认识并且附上相应的安装教程以供大家参考。接下来,我们正式进入今天的文章!!! 目录 前言 (一)P…...

浏览器跨域请求
跨域是浏览器的一种同源策略,所以该概念只存在于通过浏览器访问服务里。 如果缺少了同源策略,则浏览器的正常功能可能都会受到影响。可以说Web是构建在同源策略基础之上的,浏览器只是针对同源策略的一种实现 请求的url地址,必须与浏览器上的…...
什么,你还在用 momentJs 处理相对时间
我想,下面这段代码,你是不是在开发中常常这样使用来计算距离现在过去了多长时间: import moment from moment // 61k (gzipped:19.k) function Relative(props) {const timeString moment(props.date).fromNow()return <>{timeString…...

三维模型 工程图
飞机 Crankshaft飞机发动机手动冲压机包装成型机械-充填机械设备10数控等离子切割机床铜线缠绕机机床-磨床08机床-磨床04(附工程图)机床-车床数字纤维缠绕机机械臂液压钳机床-车床06挤出机机械手-09机械手模型库六柴油发动机中央空调机柜空调机机床-钻床三维设计电脑服务器机箱…...
:全国乙卷)
我用ChatGPT写2023高考语文作文(二):全国乙卷
2023年 全国乙卷 适用地区:河南、江西、甘肃、青海、内蒙古、宁夏、新疆、陕西 吹灭别人的灯,并不会让自己更加光明;阻挡别人的路,也不会让自己行得更远。 “一花独放不是春,百花齐放春满园。”如果世界上只有一种花朵…...

java版本工程项目管理系统平台源码,助力工程企业实现数字化管理
鸿鹄工程项目管理系统 Spring CloudSpring BootMybatisVueElementUI前后端分离构建工程项目管理系统 1. 项目背景 一、随着公司的快速发展,企业人员和经营规模不断壮大。为了提高工程管理效率、减轻劳动强度、提高信息处理速度和准确性,公司对内部工程管…...

代码随想录第55天
1.判断子序列: 动态规划五部曲分析如下: 确定dp数组(dp table)以及下标的含义 dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。 注意这里是判断s是否…...
)
算法设计与分析(填空专题)
文章目录 填空题填空题 设有一稀疏图 G,则 G 采用 邻接表 存储较省空间。 算法的时间复杂性是指算法中 元运算 执行次数。 分治法的基本思想是将一个规模为 n 的问题分解为与原问题 相同 的 k 个规模较小且互相独立的子问题。 贪心算法中每次做出的贪心选择都是 当前的 最优选…...

Ubuntu22.04 K8s1.27.2
Ubuntu22.04 && K8s1.27.2 1. 服务器配置 IpServerMEM192.168.56.11k8smaster6G192.168.56.16k8snode14G192.168.56.17k8snode24G 2. 获取源 $ sudo apt-get update $ sudo apt-get install -y apt-transport-https ca-certificates curl# packages.cloud.google.c…...
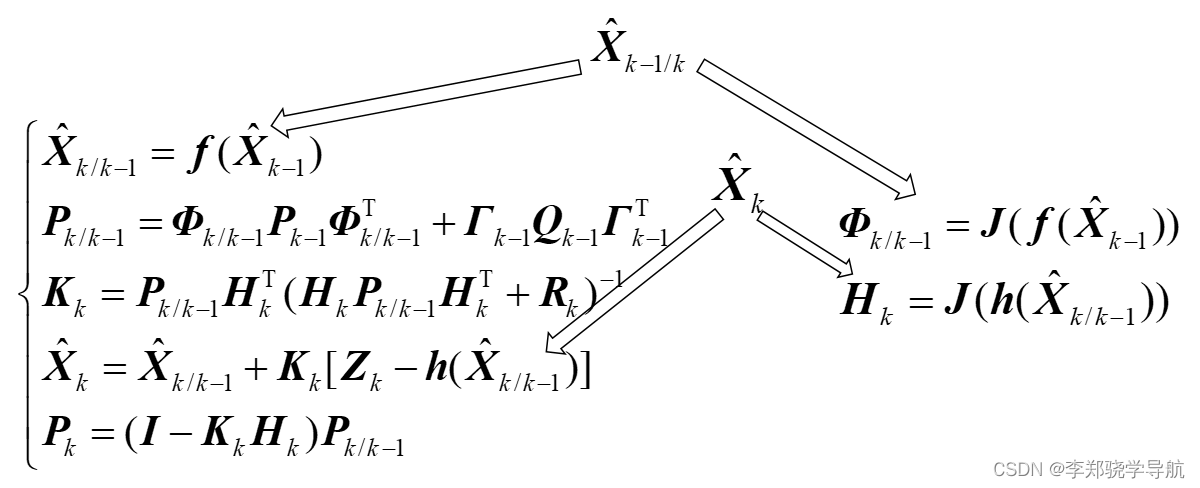
卡尔曼滤波与组合导航原理(十二)扩展卡尔曼滤波:EKF、二阶EKF、迭代EKF
文章目录 一、多元向量的泰勒级数展开二、扩展Kalman滤波三、二阶滤波四、迭代EKF滤波 一、多元向量的泰勒级数展开 { y 1 f 1 ( X ) f 1 ( x 1 , x 2 , ⋯ x n ) y 2 f 2 ( X ) f 2 ( x 1 , x 2 , ⋯ x n ) ⋮ y m f m ( X ) f m ( x 1 , x 2 , ⋯ x n ) \left\{\begin{…...
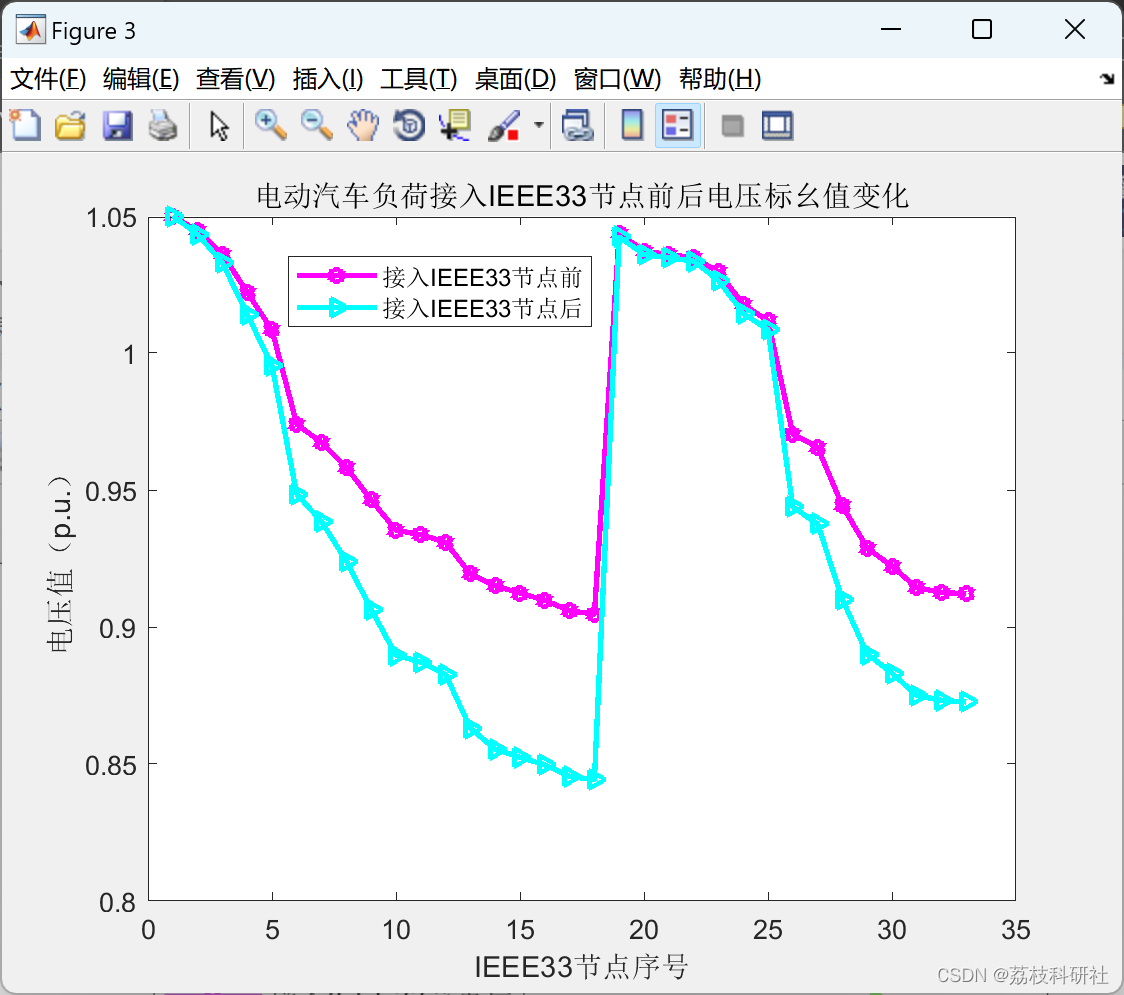
基于蒙特卡洛模拟法的电动汽车充电负荷研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
自学黑客【网络安全】,一般人我劝你还是算了吧
一、自学网络安全学习的误区和陷阱 1.不要试图先成为一名程序员(以编程为基础的学习)再开始学习 我在之前的回答中,我都一再强调不要以编程为基础再开始学习网络安全,一般来说,学习编程不但学习周期长,而…...

编程中的心理策略:如何从错误中学习并实现自我成长
在日复一日的工作中,我们免不了会产生一些失误,会因此感到沮丧和失望。但如何正确地对待和处理这些失误才是最重要的,它直接影响到我们的工作表现和个人成长。 一、面对失误而带来的指责和沮丧的策略 在程序设计领域,我们经常面临…...
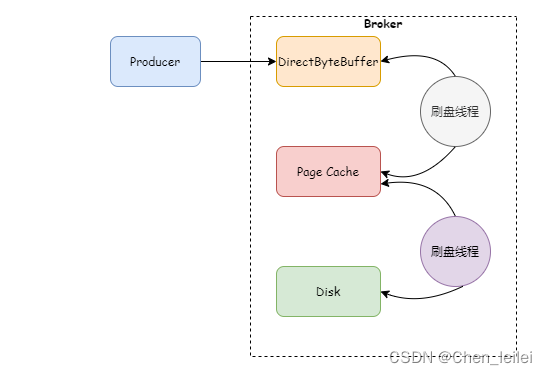
Rocket面试(五)Rocketmq发生流量控制的情况有哪些?
在使用rocketmq过程中总能看见一下异常 [TIMEOUT_CLEAN_QUEUE]broker busy, start flow control for a while, period in queue: 206ms, size of queue: 5这是因为Rocketmq出发了流量控制。 触发流量控制就是为了防止Broker压力过大挂掉。主要分为Broker流控,Consu…...

Tableau招聘信息数据可视化
获取的招聘信息数据为某招聘网站发布的大数据及数据分析相关岗位,对其他计算机相关岗位的招聘信息数据分析也有一定的参考价值。因为所获取的招聘信息数据数量只有1万左右,实际的招聘信息数量肯定不止1万,所以可能会与实际信息有一定的误差。…...
:合理应对异常)
游戏服务器开发指南(八):合理应对异常
大家好!我是长三月,一位在游戏行业工作多年的老程序员,专注于分享服务器开发相关的文章。 本文是通用程序设计主题下的第二篇。这个主题主要探讨如何编写高效、健壮、易读的游戏业务代码,每篇从一个小点切入。本次讨论的要点是&a…...

【g】聚类算法之K-means算法
聚类算法是一种无监督学习方法,它将相似的数据样本划分为一组,同时将不相似的数据样本划分为另一组。这个过程由计算机自动完成,不需要任何人为的干预。 K-means算法是一种经典的聚类算法,它的主要思想是把数据集分成k个簇&#…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
