春招Leetcode刷题日记-D4-双指针算法-滑动窗口快慢指针
D4-双指针算法-滑动窗口&&快慢指针
- 快慢指针算
- 力扣141. 环形链表
- 思路
- 代码
- 力扣142. 环形链表 II
- 思路
- 代码
- 滑动窗口
- 力扣76. 最小覆盖子串
- 思路
- 代码
- 力扣424. 替换后的最长重复字符
- 思路
- 代码
快慢指针算
快慢指针算法,多用于链表当中,常见的如:快慢指针判断链表中是否含有环路&&快慢指针找链表中点问题
力扣141. 环形链表
题目链接:141. 环形链表

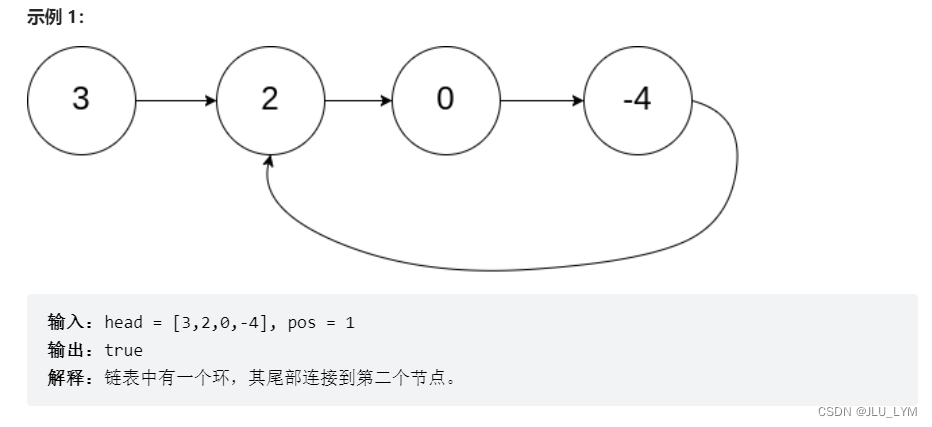

思路
这是非常经典的,Floyd判圈法,即利用快慢指针,判断链表中是否含有环路。
1、初始时,slow、fast都在开头节点
2、fast一次走两步,slow一次走一步
3、如果含有环路,二者一定在环路中相遇;反之fast先走到尾节点
代码
class Solution {
public:bool hasCycle(ListNode *head) {ListNode *slow = head, *fast = head;while (fast != nullptr&&fast->next != nullptr) {//快慢指针判断条件!!!slow = slow->next;fast = fast->next->next;if (slow == fast) {return true;}}return false;}
};力扣142. 环形链表 II
题目链接:142. 环形链表 II

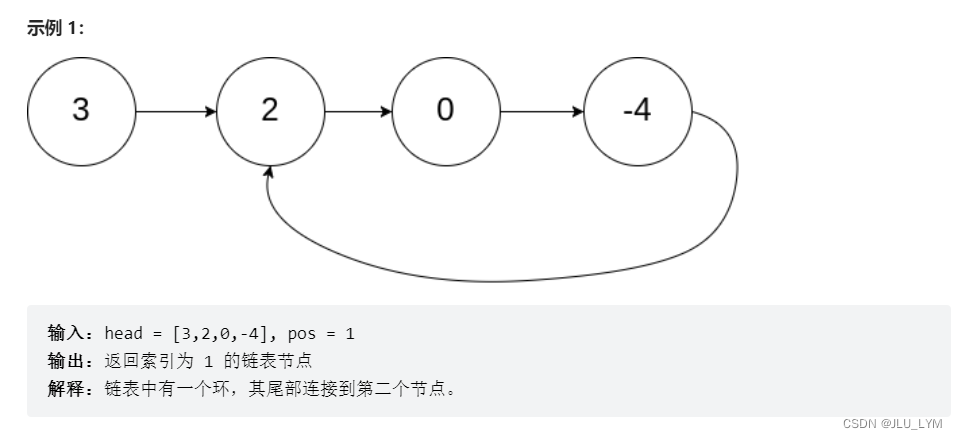

思路
本题为上一题的进阶版本,我们不仅要判断是否含有环路,还要判断环路的进入节点,并返回。
1、所以,我们第一步就是利用快慢指针,利用是否会有第一次相遇,判断出是否含有环路,思路同上一题。
2、当相遇时,二者处在环路中某一个节点,现在我们要通过分析快慢指针走过的步数,来进一步指定算法
1、设非环路部分链表共a个节点,环路部分链表共b个节点(a,b均未知,具体要看题目)
2、我们从头部出发,到达环路入口节点:要么直接走过去,即a步;要么走入环路,在环路中绕行整数个圈到达。综上,总步数为 a+nb(n为绕行圈数,为未知,看具体链表)
3、再来分析快慢指针已经走了多少步:分别设为f、s步
<1>f=2s(快指针一次两步,慢指针一次一步)
<2>f=s+nb(快慢指针都同样走过了a步,快指针多比慢指针在环路中走了几圈,且n为未知)
所以f=2nb、s=nb
4、在当下,慢指针已经走了nb步,根据上面分析,再走a步就是目标节点。但是,现在a是未知,根据上面分析,我直接从起点走a步也会到目标点。
5、综上,让快指针去链表头,让快慢指针同时按照一个速度出发,二者相遇的时候,同时走了a步,即为目标点
代码
class Solution {
public:ListNode *detectCycle(ListNode *head) {ListNode *slow = head, *fast = head;while (fast != nullptr&&fast->next != nullptr) {//快慢指针判断条件slow = slow->next;fast = fast->next->next;if (slow == fast) {//产生第一次相遇,证明含有环路,开始寻找目标点fast = head;//这里算法详见上面证明while (fast != slow) {fast = fast->next;slow = slow->next;}return slow;}}return nullptr;//不产生第一次相遇,不含有环路}
};滑动窗口
1、滑动窗口,又名双指针法,左右两个指针(l,r),同方向且l<=r,用于区间搜索。
2、只要分析出滑动窗口法之后,马上想到滑窗固定大板子:
1、滑窗之中,一定要重点统计窗口内部数据情况,这个和窗口是否收缩有很大关系
2、总体思路就是,先进行右边界扩张,更新窗口内数据信息;再根据题意判断,是否左边界++,进行窗口收缩,收缩的话,一定注意更新窗口内数据信息
3、左右指针初始化为 0 -1
int left = 0, right = -1;for (遍历一遍数组) {// c 是将移入窗口的字符char c = s[right];// 右移窗口right++;// 进行窗口内数据的一系列更新... // 判断左侧窗口是否要收缩while (左指针需要移动,即窗口需要收缩) {// d 是将移出窗口的字符char d = s[left];// 左移窗口left++;// 进行窗口内数据的一系列更新...}
力扣76. 最小覆盖子串
题目链接:76. 最小覆盖子串
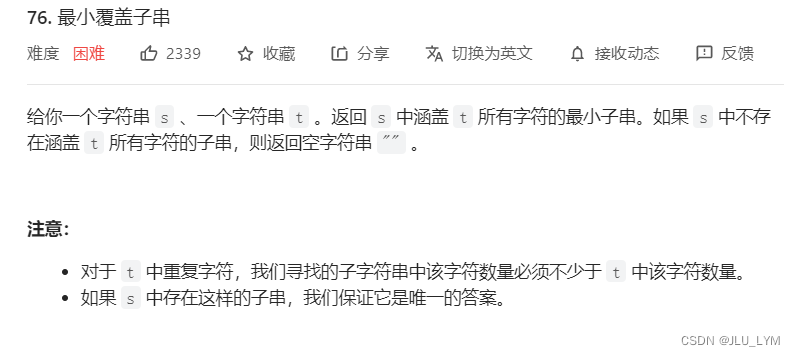

思路
本题要求我们在s中找一个片段,这个片段中必须包含t中全部出现的字母,即t中出现了2个a,那么目标片段必须出现2个a,且要求在所有满足要求的片段之中找到最短的(根据题意,答案一定唯一),这明显是区间搜索问题,马上想到滑窗法,立刻开始套模板
1、初始化 l=0,r=-1,针对滑窗,我们要统计滑窗内各个元素出现的个数,针对t,我们要统计出现了哪些元素,以及出现的次数。
2、每次先右边界++,扩充滑窗,更新滑窗内元素。
3、最重要的地方来了,如何判断是否缩小滑窗(即左边界++):如果当前滑窗内都为覆盖到所有目标元素,那么缩小滑窗之后,更是不可能覆盖。所以只有当扩充玩新元素后全覆盖到了,才考虑缩小滑窗。
4、为了看是否能达到覆盖,用sum记录还需要覆盖的字母总量,用tmp数组动态维护需要覆盖的各个字母剩余数量。
5、根据题意,当能覆盖之后,我们要这个片段尽可能的短,所以在缩小滑窗时候,当恰好排出这个元素之后,无法完全覆盖,这就代表着不缩小时,就是当前的满足要求的最短片段。所以,我们连续缩小滑窗,直到上述情况出现即可。为了让最终结果最小,要动态维护一个最短片段。
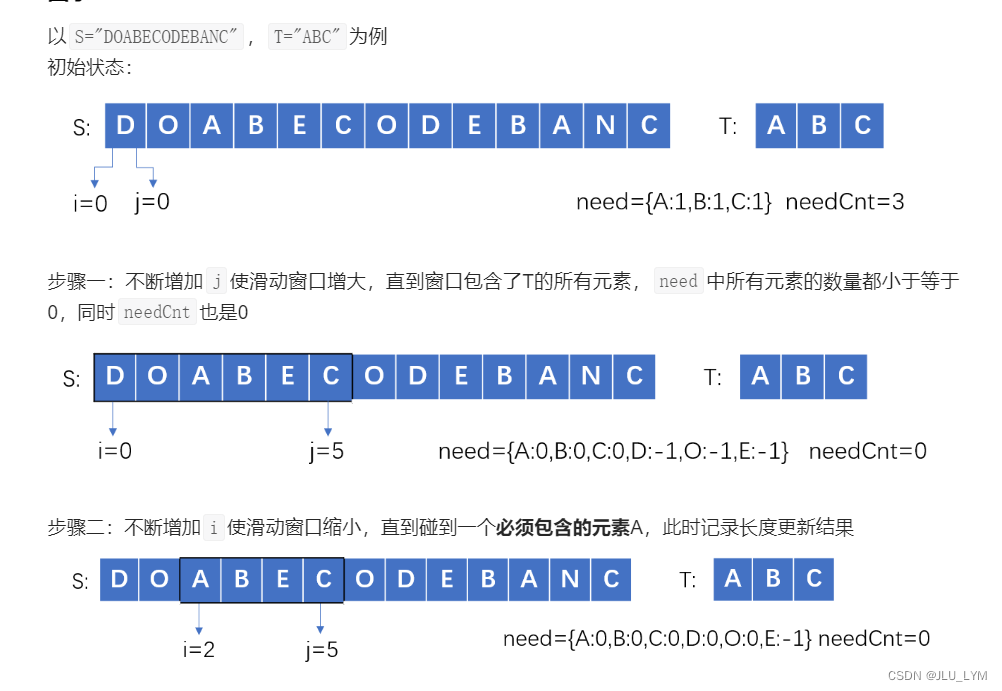
代码
注意:
1、字符串裁剪函数substr使用方式:
假设:string s = “0123456789”;
string sub1 = s.substr(5); //只有一个数字5表示从下标为5开始一直到结尾:sub1 = “56789”
string sub2 = s.substr(5, 3); //从下标为5开始截取长度为3位:sub2 = “567”
2、比如t串中只出现两个a,但窗口内出现了三个a,只有前两个算有效覆盖(既在t中出现,又满足出现次数),所以tmp就是用来动态维护这个事情
class Solution {
public:string minWindow(string s, string t) {int m = s.size(), n = t.size();//统计字符串t里面的字符信息vector<int> cnt1(128, 0);//统计t中各个字母出现的次数vector<bool> visit1(128, false);//看t中出现了哪些字母for (int i = 0; i < n; i++) {cnt1[t[i]]++;visit1[t[i]] = true;}//用来动态记录最短符合要求字串int min_l = -1, min_r = -1, mins = 1000001;//左边界,右边界,长度int l = 0, r = -1;//窗口左右指针int sum = n;//还未覆盖到的字母总数vector<int> tmp(cnt1);//复制一下cnt1,动态维护一下窗口内还需要覆盖的各个字母的个数vector<int> cnt2(128, 0);//维护窗口内所有元素出现的次数for (int i = 0; i < m; i++) {char tar = s[i];//待扩充进来的字符r++;//扩充右边界cnt2[tar]++;//更新窗口内元素出现次数//扩充进来的字母是有效的覆盖,解释看上面的注意部分if (visit1[tar] == true && tmp[tar] != 0) {sum--;//要覆盖的总数-1tmp[tar]--;//窗口内该字母还需要出现的次数-1}//开始判断是否要缩减窗口if (sum == 0) {//刚刚好,窗口扩展到全覆盖时候,才开始动左指针,找到当前状态下最小//当前窗口完全可以覆盖,为了找最小,我们收缩左边界,直到恰好覆盖(即再缩就不可以覆盖为止)//这时候,就是当前状态下最小while (sum == 0) {//连续缩小char tar2 = s[l];//待排除的元素if (visit1[tar2] == true) {//被扔出去的字母是有效字母,反之直接扔即可(l++)cnt2[tar2]--;//动态维护窗口内各字母个数,有效字母被扔出去后,它的新数量if (cnt2[tar2] < cnt1[tar2]) {//当前窗口不能恰好覆盖目标字母,这个时候就是连续缩窗口的尽头,开始更新动态维护的数据sum++;//窗口内待覆盖的元素+1if (r - l + 1 < mins) {//动态维护最小子串mins = r - l + 1;min_l = l;min_r = r;}tmp[tar2]++;//该字母在窗口内还需出现的次数+1l++;//缩窗口break;//退出连续缩窗口}}l++;}}}return min_l == -1 ? "" : s.substr(min_l, min_r-min_l+1);//始终未找到合适的窗口,min_l==-1,返回空串;反之按照大小裁剪目标串s}
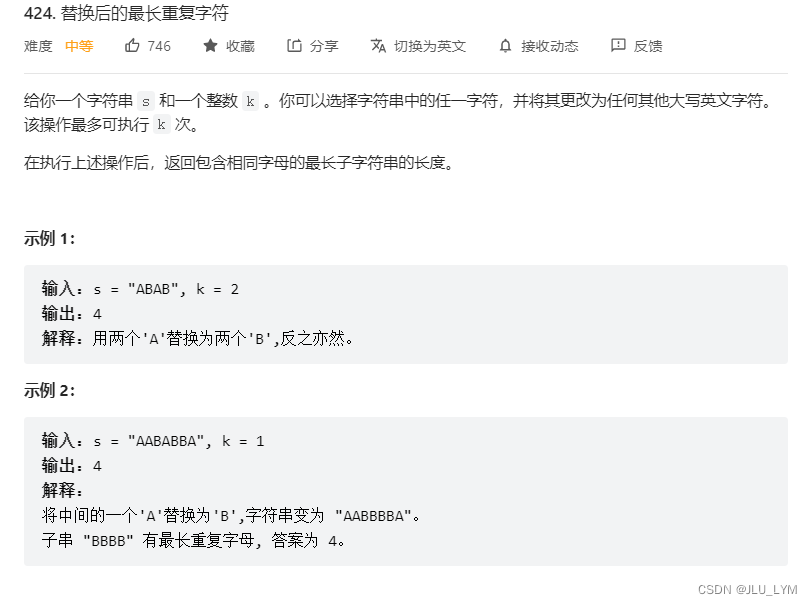
};力扣424. 替换后的最长重复字符
题目链接424. 替换后的最长重复字符
思路
明显的,在大区间中,找一个连续的小区间,经过不多于k次的变化之后,让其中元素都统一,且这个片段要最长。区间搜索,马上想滑窗,上模板:
1、初始化 l=0 ;r=-1 ;统计窗口内各个元素个数;一个窗口内,为了在有限的替换之后,整体最长,肯定是维护一个个数最多的元素,把和他不同的全换下去,这样才会最长,也能最大程度上利用k,所以维护窗口内最大元素个数
2、r++,扩充窗口,更新元素数量,因为该字母变多了,可能成为最多的个数,所以也要维护窗口内最大元素个数
3、滑窗问题关键来了,缩小窗口:当”非最多数量元素“个数小于等于k(可替换数量),说明这次扩充是可以的,窗口确实可以扩张,不需要收缩(因为题目要的就是最长),反之,就得收缩,更新的数据同上
代码
class Solution {
public:int characterReplacement(string s, int k) {int n = s.size();vector<int> cnt(26, 0);//窗口各个字母个数int l = 0, r = -1;int maxs = 0;for (int i = 0; i < n; i++) {char tar = s[i];//待扩充元素r++;//扩充cnt[tar - 'A']++;//两次更新数据maxs = max(maxs, cnt[tar - 'A']);if (r - l + 1 - maxs > k) {//扩充失败了,必须要收缩一下char tmp = s[l];cnt[tmp - 'A']--;for (int j = 0; j < 26; j++) {maxs = max(maxs, cnt[j]);}l++;}}return r - l + 1;}
};
相关文章:

春招Leetcode刷题日记-D4-双指针算法-滑动窗口快慢指针
D4-双指针算法-滑动窗口&&快慢指针快慢指针算力扣141. 环形链表思路代码力扣142. 环形链表 II思路代码滑动窗口力扣76. 最小覆盖子串思路代码力扣424. 替换后的最长重复字符思路代码快慢指针算 快慢指针算法,多用于链表当中,常见的如࿱…...
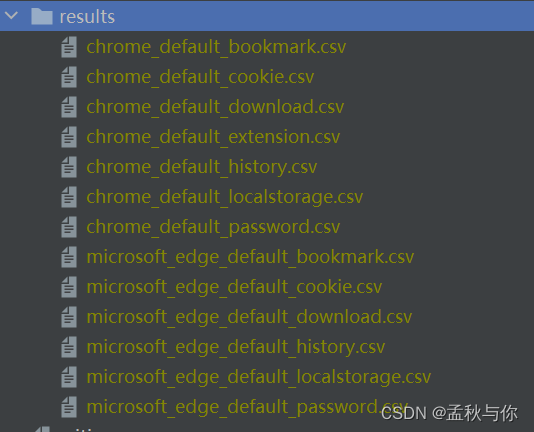
【go】结合一个go开源项目分析谷歌浏览器cookie为什么不安全 附go项目导包失败怎么解决教程
本文创作背景 源于谷歌浏览器提示密码被泄露 并且某站很快收到了异地企图登录的提醒。 当即怀疑是不是谷歌浏览器保存的密码不安全,最后查阅诸多资料 并找到一个go语言编写的开源项目进行研究,虽然最终不能确定密码是如何泄露的 但研究结论还是让人不由感…...

Windows瘦身方法
一、快速删除系统盘临时文件方法, 1、winr打开运行对话框,输入%temp%命令,如图1 图1 2、打开temp文件夹,如图2,选择所有文件,鼠标右键删除或按Del键删除。 图2 二、磁盘清理 1、winr,输入cleanmgr&#x…...
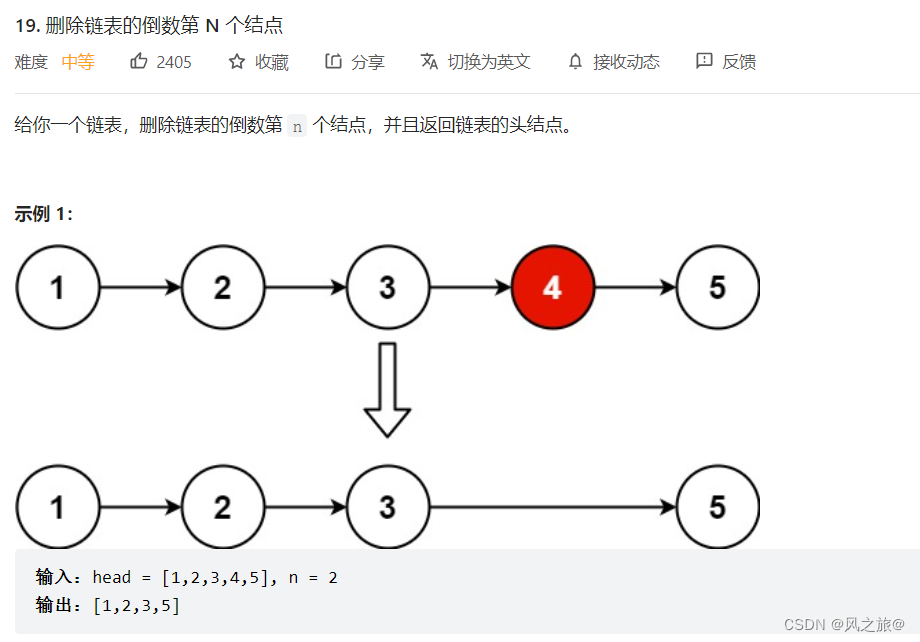
19. 删除链表的倒数第 N 个结点
题目链接:https://leetcode.cn/problems/remove-nth-node-from-end-of-list/进阶:你能尝试使用一趟扫描实现吗?解题思路:最简单的方法是先遍历一次链表,得到链表的长度len,然后再一次遍历链表,遍…...
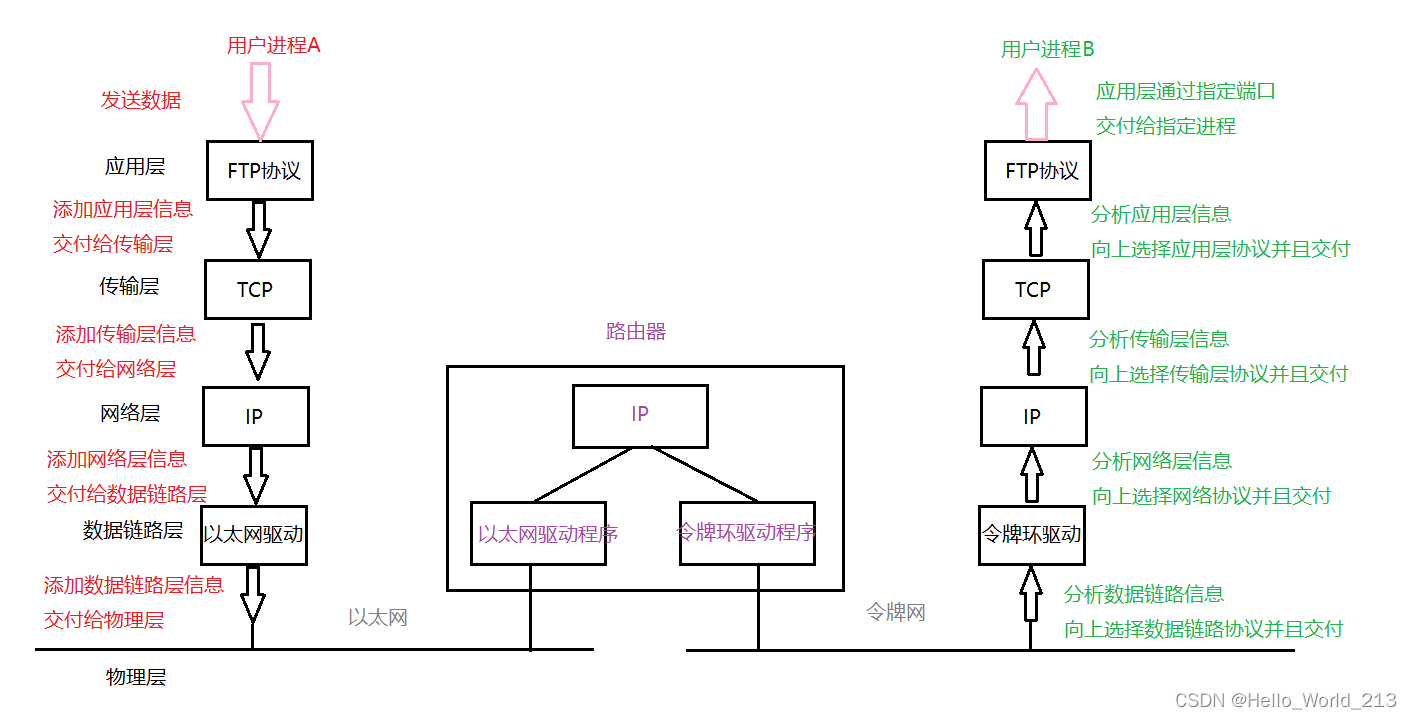
【Linux】网络编程 - 基础概念
目录 一.OSI七层模型vsTCP/IP五层模型 1.一些周边概念 2.OSI七层模型 3.TCP/IP五层模型 4.网络传输流程图 二.什么是MAC地址 三.什么是IP/IP地址 1.什么是IP 2.什么是IP地址 四.什么是端口号 一.OSI七层模型vsTCP/IP五层模型 1.一些周边概念 局域网vs广域网 网络互…...

Unity 多语言 轻量高效的多语言工具集 LanguageManager
效果展示 支持excel导入自动化 组件化 更方便 也提供直接获取多语言的接口 没有挂 LanguageText的对象也可以获取多语言文本内容 支持 Format接口 可以传递N个参数进来组装多语言 支持首次系统语言自测 支持语言切换后本地自动保存配置 支持实时切换 同步刷新所有UI 容错处…...

在Linux和Windows上安装zookeeper-3.5.9
记录:378场景:在CentOS 7.9操作系统上,安装zookeeper-3.5.9。在Windows上操作系统上,安装zookeeper-3.5.9。版本:JDK 1.8 CentOS 7.9 zookeeper-3.5.9官网地址:https://zookeeper.apache.org/源码地址&…...
【ESP32+freeRTOS学习笔记-(八)资源管理】
目录1、 资源使用概况2、互斥方法之一:基本临界区2.1、taskENTER_CRITICAL_FROM_ISR() 和taskEXIT_CRITICAL_FROM_ISR()3、互斥方法之二:挂起或锁定调度程序3.1 vTaskSuspendAll()3.2 xTaskResumeAll()4 互斥方法三:互斥信号量(和…...
)
P1427 小鱼的数字游戏(赋值运算符和String)
小鱼的数字游戏 题目描述 小鱼最近被要求参加一个数字游戏,要求它把看到的一串数字 aia_iai(长度不一定,以 000 结束),记住了然后反着念出来(表示结束的数字 000 就不要念出来了)。这对小鱼…...

Java学的好,工作不愁找
俗话说的好:“Java学的好,工作不愁找”,不管我们学习哪一门语言,我们都要掌握从抽象化中提取出来的方法,这样你才能提高我们的学习能力,并且在学习新事物的时候可以提取我们自己的想法。学习java࿰…...

表情包可视化编辑、生成配置信息数据工具
合成GIF图片 - 表情包 后续,用于快速、便捷生成 img_config.js 中 要生成的GIF每一帧数据(写入头像图片信息参数); 1、先上传 写入GIF中头像 标准图,同时获取图片信息,更新 写入GIF中头像 初始值࿰…...

java简单循环结构
while循环结构 Java提供的while条件循环。它的基本用法是: while (条件表达式) {循环语句 } // 继续执行后续代码while循环在每次循环开始前,首先判断条件是否成立。如果计算结果为true,就把循环体内的语句执行一遍,如果计算结果…...
【Servlet+Jsp+Mybatis+Maven】WEB图书馆管理系统
web图书馆管理系统一、绪论二、流程和其页面展示效果流程页面效果项目结构三、具体实现第一步:备数据库表第二步:编写登录前端代码第三步:利用过滤器处理安全问题第四步:控制层去实现相关调用第五步:实现持久化层与数据…...
【WPF】WindowChrome 自定义窗口完美实现
WindowChrome 自定义窗口完美实现简介效果图自定义最小化、最大化、关闭按钮布局实现结语简介 Microsoft官网关于 WindowChome 的介绍 截取Microsoft文章的一段话: 若要在保留其标准功能时自定义窗口,可以使用该 WindowChrome 类。 该 WindowChrome…...
Python客户端使用SASL_SSL连接Kafka需要将jks密钥转换为pem密钥,需要转化成p12格式再转换pem才能适配confluent_kafka包
证书生成 生成证书以及jks参考以下文章 https://blog.csdn.net/qq_41527073/article/details/121148600 证书转换jks -> pem 需要转化成p12以下转换才能适配confluent_kafka包,直接jks转pem会报错不能使用,具体参考以下文章 https://www.ngui.cc/z…...

JDK8 ConcurrentHashMap源码分析
文章目录常量说明put() 方法putVal() 方法initTable():初始化数组treeifyBin():链表转红黑树tryPresize():初始化数组扩容TreeBin() 构造方法:生成红黑树putTreeVal():往红黑树中插入值helpTransfer():多线…...

前置知识-初值问题、欧拉法、改进欧拉法
1.1 初值问题 初值问题是科研、工程技术应用中最常见的一类问题, 一阶常微分方程的初值问题表述如下: 已知 u ( x ) u(x) u(x) 的起始点 ( x 0 , u 0 ) \left(x_0, u_0\right)...

睡眠影响寿命,这几个睡眠习惯赶紧改掉!
我们知道,现在睡眠不足已经成为普遍问题,但你知道睡眠的时长会影响寿命吗?熬夜对身体不好,已是老生常谈。但睡得过早,也可能影响寿命!2021年《睡眠医学》杂志一项针对21个国家11万名参与者的研究中发现&…...

Linux逻辑卷管理器(PV、VG、LV、PE)
目录 PV阶段 VG阶段 LV阶段 文件系统阶段 逆向操作(删除LVM) 逻辑卷管理器(Logical Volume Manager),简称LVM LVM的做法是将几个物理的分区(或磁盘)通过软件组合成为一块看起来时独立的大…...
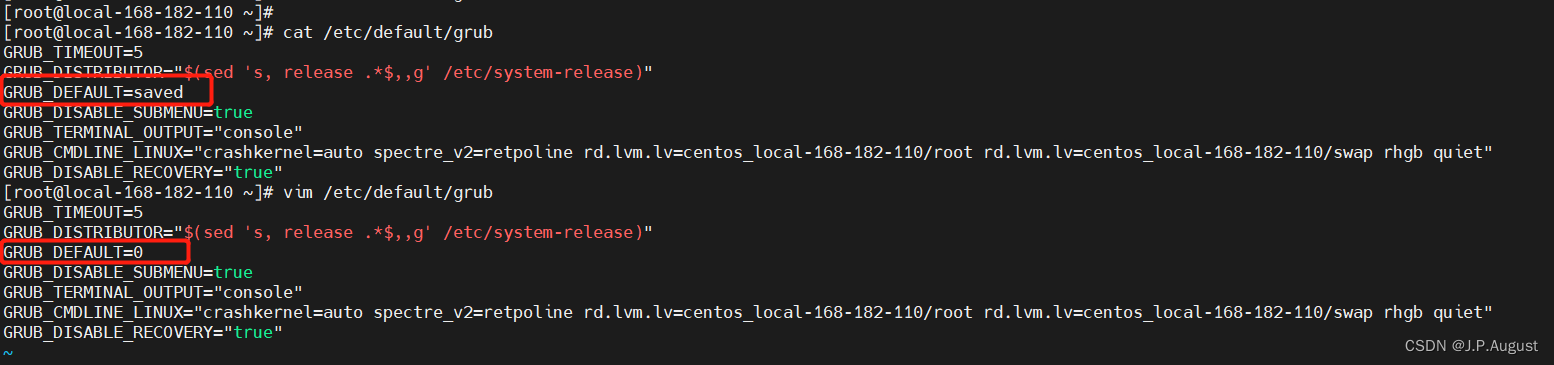
Centos7 内核升级
一、背景 在 CentOS 使用过程中,高版本的应用环境可能需要更高版本的内核才能支持,所以难免需要升级内核,所以下面将介绍yum和rpm两种升级内核方式。 关于内核种类: kernel-ml——kernel-ml 中的ml是英文【 mainline stable 】的缩写&…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
