Python3数据分析与挖掘建模(13)复合分析-因子关分析与小结
1.因子分析
1.1 探索性因子分析
探索性因子分析(Exploratory Factor Analysis,EFA)是一种统计方法,用于分析观测变量之间的潜在结构和关联性。它旨在确定多个观测变量是否可以归结为较少数量的潜在因子,从而帮助简化数据集和提取隐藏的信息。
在探索性因子分析中,我们收集一组观测变量的数据,并试图找到解释这些变量之间关系的较少数量的潜在因子。这些潜在因子是无法直接观测到的,但它们可以通过变量之间的共同方差来解释观测数据的模式。
探索性因子分析的主要目标是确定以下内容:
- 因子结构:通过观察变量之间的共同变异性,确定潜在因子的数量和性质。
- 因子载荷:衡量每个变量与每个因子之间的关系强度。较高的因子载荷表示变量与因子之间存在较强的关联。
- 因子解释:解释每个因子所代表的潜在构念或概念。这可以通过变量与因子之间的关系和变量的解释程度来实现。
探索性因子分析可以用于数据降维、构建测量工具、发现潜在因素和进行模型建立等领域。它被广泛应用于社会科学、心理学、教育、市场研究等领域,以揭示变量之间的潜在结构和解释现象背后的因素。
主成分分析:
主成分分析是一种降维技术,它旨在将高维数据转化为较低维度的表示,同时尽可能保留原始数据的信息。主成分分析通过线性变换将原始变量转化为一组互相无关的主成分,其中每个主成分都是原始变量的线性组合。这些主成分按照其解释的方差大小排序,通常只保留方差较大的主成分。
在探索性因子分析中,主成分分析被用于确定潜在因子的数量和性质。它通过计算每个主成分的方差贡献和特征载荷(变量与主成分之间的相关系数)来帮助解释原始变量之间的相关性和共同性。主成分分析可以帮助识别潜在因子,并提供每个变量对于每个主成分的贡献程度。
主成分分析的步骤通常包括以下内容:
- 数据准备:收集相关变量的观测数据,并进行数据清洗和预处理。
- 计算协方差矩阵或相关系数矩阵:根据数据的特点,计算变量之间的协方差矩阵或相关系数矩阵。
- 提取主成分:使用特征值分解或奇异值分解等方法,计算协方差矩阵的特征值和特征向量,从中提取主成分。
- 解释方差贡献:计算每个主成分的方差贡献,并确定保留的主成分数量。
- 解释主成分:通过观察主成分与原始变量之间的特征载荷,解释每个主成分所代表的意义和含义。
- 结果解释:根据主成分的解释和方差贡献,解释原始变量之间的相关性和共同性,推断潜在因子结构。
主成分分析在数据降维、变量选择、特征提取等领域有广泛应用。它可以帮助简化复杂的数据集,减少变量的数量,并提供变量之间的结构信息。主成分分析在数据预处理、数据挖掘、模式识别等领域中发挥着重要作用,为后续分析和解释提供
1.2 验证性因子分析
验证性因子分析(Confirmatory Factor Analysis,CFA)是一种结构方程模型的方法,用于验证已经提出的潜在因子结构模型是否与观测数据相符。
在验证性因子分析中,研究者根据理论或先前的研究假设一个潜在因子结构模型,然后使用观测数据来评估该模型与实际数据的拟合程度。验证性因子分析的目标是确定潜在因子模型是否能够恰当地解释观测变量之间的关系,并提供有关模型拟合程度的统计指标。
在验证性因子分析中,常用的评估指标和统计方法包括:
-
相关性(Correlation):通过计算观测变量之间的相关系数,评估模型中潜在因子之间的关联程度。
-
卡方检验(Chi-Square Test):用于评估观测数据与模型之间的拟合程度。卡方检验比较观测数据与理论模型之间的差异,若差异较小,则说明模型与数据拟合较好。
-
覆盖度(Coverage):评估模型中的潜在因子是否能够覆盖观测变量的变异。覆盖度可以通过计算模型中潜在因子的方差贡献或占总变异的比例来衡量。
-
方差分析(ANOVA):用于评估模型中不同组别之间的差异程度。方差分析可以帮助检验潜在因子模型是否能够解释观测数据中的组别差异。
-
熵(Entropy):用于衡量模型中潜在因子的信息量和不确定性。熵越小表示模型解释观测数据的能力越强。
-
F-值(F-Value):用于比较模型拟合指标在不同模型之间的差异。F-值可以帮助确定是否存在更好的模型来解释观测数据。
-
自定义指标:根据研究者的需求,可以定义和使用其他适用的指标和统计方法来评估验证性因子分析模型的拟合程度和解释能力。
验证性因子分析是一种复杂的数据分析方法,需要具备统计学和结构方程模型的知识。在实际应用中,通常使用统计软件(如R、SPSS、AMOS等)来执行验证性因子分析,并根据评估指标进行模型拟合和解释。
2. 主成分分析实例
2.1 代碼
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.decomposition import PCA #用于执行主成分分析。sns.set_context(font_scale=1.5)
df = pd.read_csv("../data/HR.csv")# 处理缺失值
df = df.dropna() # 删除包含缺失值的行my_pca = PCA(n_components=7)
lower_mat = my_pca.fit_transform(df.drop(labels=["salary", "department", "left"], axis=1))
print("Ratio:", my_pca.explained_variance_ratio_)sns.heatmap(pd.DataFrame(lower_mat).corr(), vmin=-1, vmax=1, cmap=sns.color_palette("RdBu", n_colors=128))
plt.show()-
处理缺失值:
- 使用
dropna()函数删除包含缺失值的行,更新df。
- 使用
-
创建PCA对象
my_pca,并设置要提取的主成分数量为7。 -
使用
fit_transform()方法对从df中删除 "salary"、"department" 和 "left" 列后的数据执行主成分分析。将结果存储在lower_mat中。 -
打印主成分的解释方差比例,即每个主成分所解释的方差的比例。
-
使用
seaborn的heatmap()函数创建相关性热图,传入pd.DataFrame(lower_mat).corr()作为相关性矩阵,设置颜色映射为"RdBu"色板,并指定颜色范围。 -
使用
plt.show()显示绘制的热图。
总体而言,这段代码的目的是通过主成分分析对数据进行降维,并可视化主成分之间的相关性。它可以帮助我们理解数据的结构和特征之间的关系。
2.2 分析结果
Ratio: [9.98565312e-01 8.69277622e-04 4.73866604e-04 4.96913206e-052.43160255e-05 9.29566680e-06 8.24092853e-06]结果显示了主成分分析中每个主成分所解释的方差比例。具体来说,结果为:
- 第一个主成分解释了总方差的约99.86%。
- 第二个主成分解释了总方差的约0.09%。
- 第三个主成分解释了总方差的约0.05%。
- 第四个主成分解释了总方差的约0.005%。
- 第五个主成分解释了总方差的约0.002%。
- 第六个主成分解释了总方差的约0.001%。
- 第七个主成分解释了总方差的约0.001%。
这些方差比例表示了每个主成分对数据中的变异程度的贡献。第一个主成分的方差比例最大,说明它包含了最多的信息。随着主成分的编号递增,方差比例逐渐减小,表明后续的主成分解释的方差较小,包含的信息量也较少。
这些方差比例可用于确定选择多少个主成分以保留数据中的有效信息。通常,我们可以选择累计方差比例达到一定阈值(如90%或95%)的主成分作为降维后的特征。
2.3 效果热图
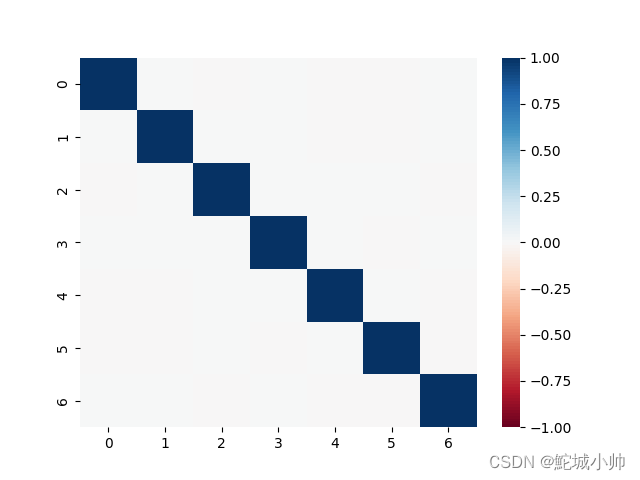
通过主成分分析热图可知,只有对角线上的相关系数几乎为1,其他区域几乎为零,几乎不相关。所以说,主成分分析把原来的特征空间变成了正交的特征空间。
主成分分析将原始特征空间转换为正交的特征空间。在转换后的特征空间中,主成分之间几乎没有相关性,即主成分之间的相关系数接近零,而主成分自身的相关系数接近1。
这种正交性意味着主成分是相互独立的,每个主成分捕捉到数据中的不同方差来源。第一个主成分解释了最大的方差,它是数据中变化最大的方向。随后的主成分依次解释了剩余的方差,并与之前的主成分正交。
因此,通过主成分分析,我们可以通过选择具有较高方差比例的主成分来减少特征的维度,并保留数据中最重要的信息。同时,正交的特征空间使得主成分之间彼此独立,降低了多重共线性的问题,更方便进行后续的统计分析和建模。
3. 小结
3.1 数据集类型与分析方法选择
| 数据类型 | 可用方法 |
| 连续---连续 | 相关系数、假设检验 |
| 连续---离散(二值) | 相关系数,连续二值化(最小Gini切分,最大熵增益切分) |
| 连续---离散(非二值) | 相关系数(定序) |
| 离散(二值)--- 离散(二值) | 相关系数,熵相关,F分值 |
| 离散--- 离散(非二值) | 熵相关,Gini,相关系数(定序) |
相关文章:

Python3数据分析与挖掘建模(13)复合分析-因子关分析与小结
1.因子分析 1.1 探索性因子分析 探索性因子分析(Exploratory Factor Analysis,EFA)是一种统计方法,用于分析观测变量之间的潜在结构和关联性。它旨在确定多个观测变量是否可以归结为较少数量的潜在因子,从而帮助简化…...
【stable diffusion】图片批量自动打标签、标签批量修改(BLIP、wd14)用于训练SD或者LORA模型
参考: B站教学视频【:AI绘画】新手向!Lora训练!训练集准备、tag心得、批量编辑、正则化准备】官方教程:https://github.com/darkstorm2150/sd-scripts/blob/main/docs/train_README-en.md#automatic-captioning 一、…...

TCP可靠数据传输
TCP的可靠数据传输 1.TCP保证可靠数据传输的方法 TCP主要提供了检验和、序号/确认号、超时重传、最大报文段长度、流量控制等方法实现了可靠数据传输。 检验和 通过检验和的方式,接收端可以检测出来数据是否有差错和异常,假如有差错就会直接丢失该TC…...

Python 私有变量和私有方法介绍
Python 私有变量和私有方法介绍 关于 Python 私有变量和私有方法,通常情况下,开发者可以在方法或属性名称前加上单下划线(_),以表示该方法或属性仅供内部使用,但这只是一种约定,并没有强制执行禁…...
Kotlin Lambda表达式和匿名函数的组合简直太强了
Kotlin Lambda表达式和匿名函数的组合简直太强了 简介 首先,在 Kotlin 中,函数是“第一公民”(First Class Citizen)。因此,它们可以被分配为变量的值,作为其他函数的参数传递或者函数的返回值。同样&…...

uniapp 小程序 获取手机号---通过前段获取
<template><!-- 获取手机号,登录内容 --><view><!-- 首先需要先登录获取code码,然后才可以获取用户唯一标识openid以及会话密钥及用于解密获取手机的加密信息 --><view click"login">登录</view><view…...

面板安全能力持续增强,新增日志审计功能,1Panel开源面板v1.3.0发布
2023年6月12日,现代化、开源的Linux服务器运维管理面板1Panel正式发布v1.3.0版本。 在这一版本中,1Panel进一步增强了安全方面的能力,包括新增SSH配置管理、域名绑定和IP授权支持,以及启用网站防盗链功能。此外,该版本…...
k8s学习-CKS考试必过宝典
目录 CKS考纲集群安装:10%集群强化:15%系统强化:15%微服务漏洞最小化:20%供应链安全:20%监控、日志记录和运行时安全:20% 报名模拟考试考试注意事项考前考中考后 参考 CKS考纲 集群安装:10% 使…...

jmeter如何将上一个请求的结果作为下一个请求的参数
目录 1、简介 2、用途 3、下载、简单应用 4、如何将上一个请求的结果作为下一个请求的参数 1、简介 在JMeter中,可以通过使用变量来将上一个请求的结果作为下一个请求的参数传递。 ApacheJMeter是Apache组织开发的基于Java的压力测试工具。用于对软件做压力测…...

JAVA如何学习爬虫呢?
学习Java爬虫需要掌握以下几个方面: Java基础知识:包括Java语法、面向对象编程、集合框架等。 网络编程:了解HTTP协议、Socket编程等。 HTML、CSS、JavaScript基础:了解网页的基本结构和样式,以及JavaScript的基本语…...

距离保护原理
距离保护是反映故障点至保护安装处的距离,并根据距离的远近确定动作时间的一种保护。故障点距保护安装处越近,保护的动作时间就越短,反之就越长,从而保证动作的选择性。测量故障点至保护安装处的距离,实际上就是用阻抗…...
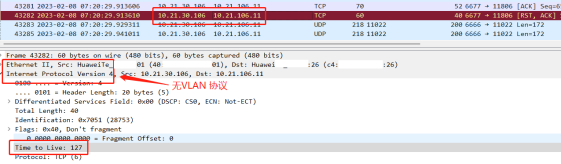
从微观世界的RST包文视角助力企业网络应用故障排查和优化
1. 前言 随着互联网的普及和发展,各行业的业务和应用越来越依赖于网络。然而,网络环境的不稳定性和复杂性使得出现各种异常现象的概率变得更高了。这些异常现象会导致业务无法正常运行,给用户带来困扰,甚至影响企业的形象和利益。…...

企业微信开发,简单测试。
企业微信开发,参考文档: https://github.com/wechat-group/WxJava/wiki...

element日期选择设置默认时间el-date-picker
<el-date-pickerv-model"rangeDate"style"width:350px"type"daterange"value-format"yyyy-MM-dd"change"dataChange"start-placeholder"开始日期"end-placeholder"结束日期"></el-date-picker…...
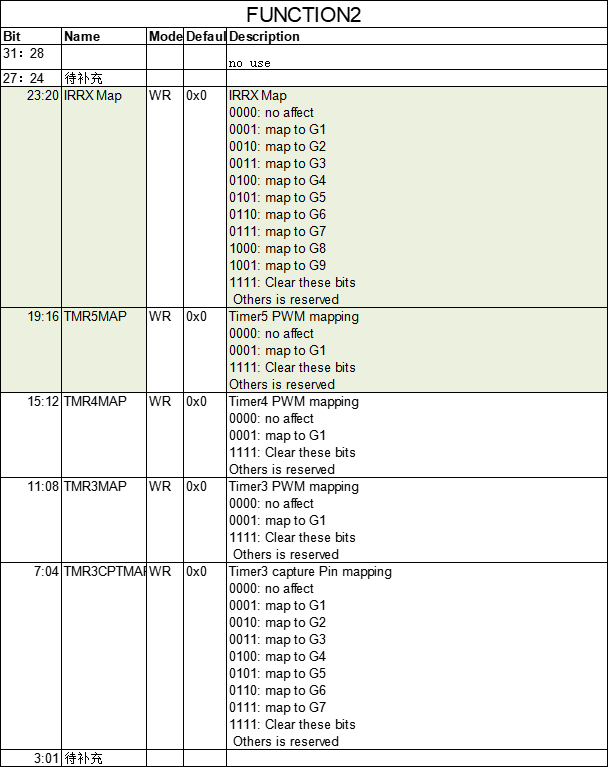
AB32VG:SDK_AB53XX_V061(3)IO口复用功能的补充资料
文章目录 1.IO口功能复用表格2.功能映射寄存器 FUNCTION03.功能映射寄存器 FUNCTION14.功能映射寄存器 FUNCTION2 AB5301A的官方数据手册很不完善,没有开放出来。我通过阅读源码补充了一些关于IO口功能复用寄存器的资料。 官方寄存器文档:《 AB32VG1_Re…...

UnityVR--组件10--UGUI简单介绍
目录 前言 UI基础组件 1. Canvas 2. EventSystem 3. Image 4. Text/TextMeshPro/InputField 5. Button控件 其他 前言 UGUI是Unity推出的新的UI系统,它与Unity引擎结合得更紧密,并拥有强大的屏幕自适应和更简单的深度处理机制,更容易使用和…...
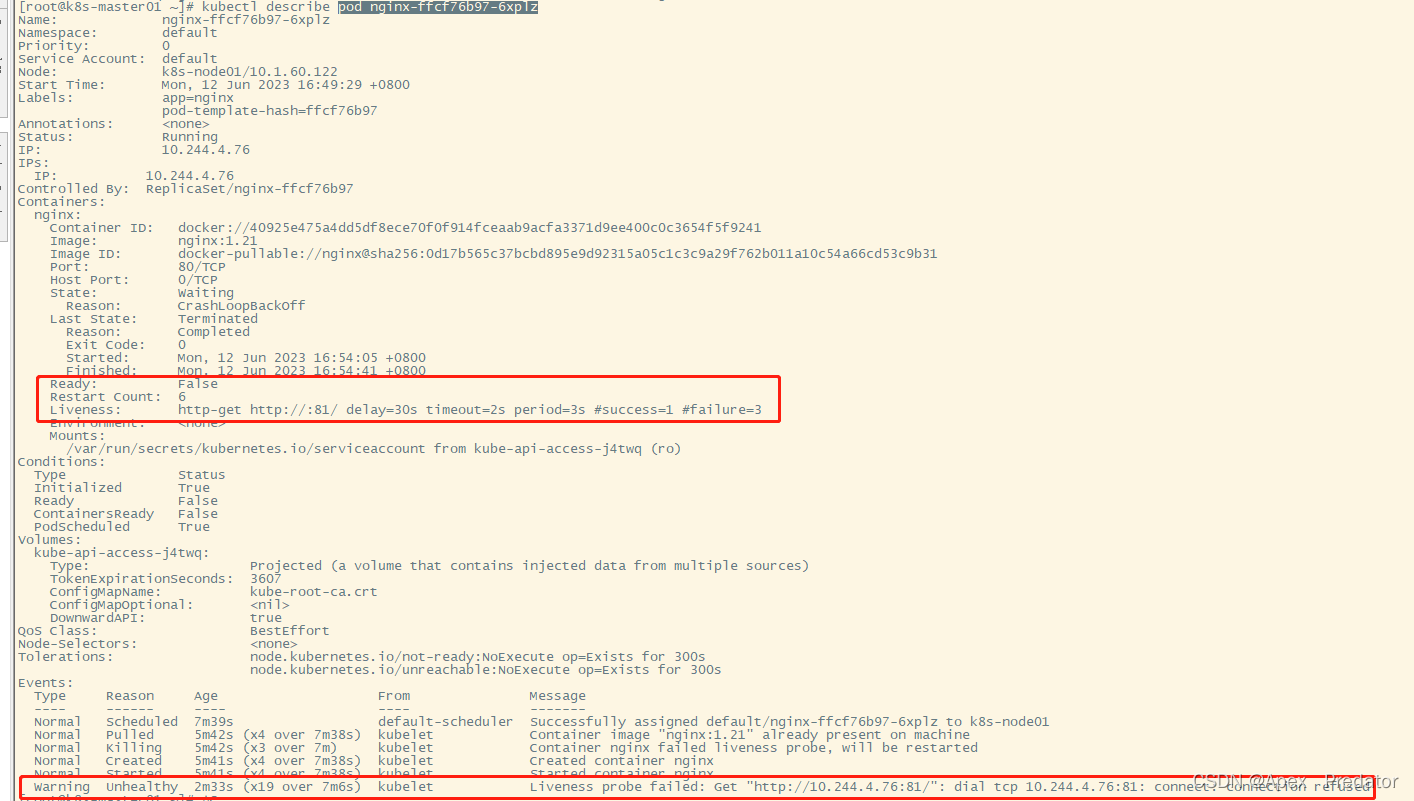
k8s 探针
1.前言 Kubernetes探针(Probe)是用于检查容器运行状况的一种机制。探针可以检查容器是否正在运行,容器是否能够正常响应请求,以及容器内部的应用程序是否正常运行等。在Kubernetes中,探针可以用于确定容器的健康状态,如果容器的健…...

【爬虫】4.4 Scrapy 爬取网站数据
目录 1. 建立 Web 网站 2. 编写 Scrapy 爬虫程序 为了说明 scrapy 爬虫爬取网站多个网页数据的过程,用 Flask 搭建一个小型的 Web 网站。 1. 建立 Web 网站 (1)books.html <!DOCTYPE html> <html lang"en"> <h…...

PureComponent和Component的区别和底层处理机制
PureComponent和Component都是React中的组件类,但它们在实现细节和使用上有些差别。 Component是React中定义组件的基类,它的shouldComponentUpdate方法默认返回true,也就是说,每次调用setState或forceUpdate方法都会引发组件重新…...
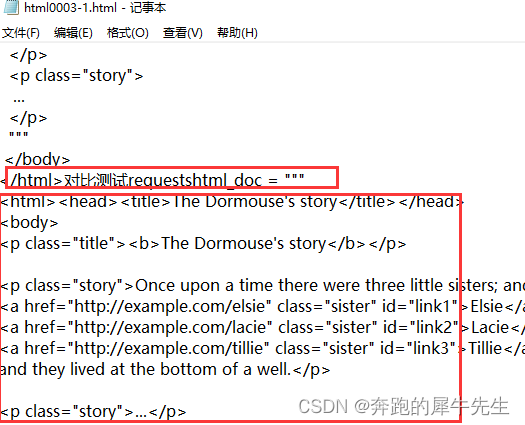
python3 爬虫相关学习9:BeautifulSoup 官方文档学习
目录 1 BeautifulSoup 官方文档 报错暂时保存 2 用bs 和 requests 打开 本地html的区别:代码里的一段html内容 2.1 代码和运行结果 2.2 用beautiful 打开 本地 html 文件 2.2.1 本地html文件 2.2.2 soup1BeautifulSoup(html1,"lxml") 2.3 用reque…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
