python基础知识(十三):numpy库的基本用法
目录
- 1. numpy的介绍
- 2. numpy库产生矩阵
- 2.1 numpy将列表转换成矩阵
- 2.2 numpy创建矩阵
- 3. numpy的基础运算
- 4. numpy的基础运算2
- 5. 索引
1. numpy的介绍
numpy库是numpy是python中基于数组对象的科学计算库。
2. numpy库产生矩阵
2.1 numpy将列表转换成矩阵
import numpy as nparray = np.array([[1, 2, 3],[4, 5, 7]]) # 将列表转换成矩阵
print(array) # 输出矩阵
print('number of dim', array.ndim) # 输出矩阵的维度
print('shape', array.shape) # 输出矩阵的形状
print('size', array.size) # 输出矩阵的大小
在这段代码中,首先导入numpy库,然后使用array()方法将列表转换成矩阵。

2.2 numpy创建矩阵
- 使用array()方法产生一维和二维矩阵
import numpy as np
# 一维矩阵
a = np.array([2, 3, 4], dtype=np.int64)
print(a, a.dtype)# 二维矩阵
a = np.array([[1, 2, 3],[4, 5, 6]])
print(a)

- 使用zeros()方法产生全0矩阵
# 0矩阵
a = np.zeros((3, 4))
print(a)

- 使用ones()方法产生全1矩阵
# 1矩阵
a = np.ones((3, 4))
print(a)

- 使用arrange()方法产生均匀矩阵、
# 均匀矩阵
a = np.arange(10, 20, 2) # 10-20,步长为2
print(a)
a = np.arange(12).reshape((3, 4)) # 将形状改变成3*4
print(a)

- 使用linspace()方法产生一维行向量
# 一维行向量
a = np.linspace(1, 10, 6)
print(a)
a = np.linspace(1, 10, 6).reshape((2, 3))
print(a)
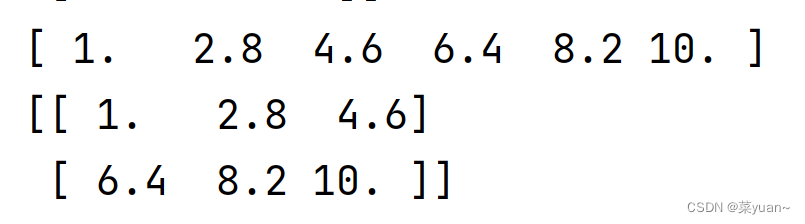
- 完整代码
import numpy as np
# 一维矩阵
a = np.array([2, 3, 4], dtype=np.int64)
print(a, a.dtype)# 二维矩阵
a = np.array([[1, 2, 3],[4, 5, 6]])
print(a)# 0矩阵
a = np.zeros((3, 4))
print(a)# 1矩阵
a = np.ones((3, 4))
print(a)# 均匀矩阵
a = np.arange(10, 20, 2) # 10-20,步长为2
print(a)
a = np.arange(12).reshape((3, 4)) # 将形状改变成3*4
print(a)# 一维行向量
a = np.linspace(1, 10, 6)
print(a)
a = np.linspace(1, 10, 6).reshape((2, 3))
print(a)
3. numpy的基础运算
- 加法运算
import numpy as npa = np.array([10, 20, 30, 40])
b = np.arange(4)
print(b)
# 加法
c = a + b
print(c)
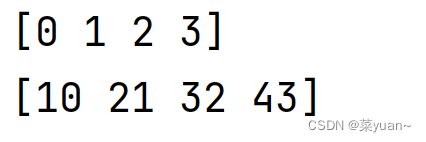
- 减法运算
# 减法
c = a - b
print(c)
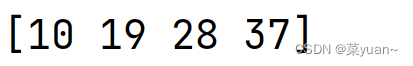
- 乘方运算
# 乘方
b = b ** 2
print(b)
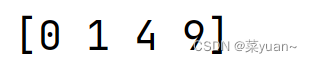
- 正弦运算
# 正弦
c = 10 * np.sin(a)
print(c)
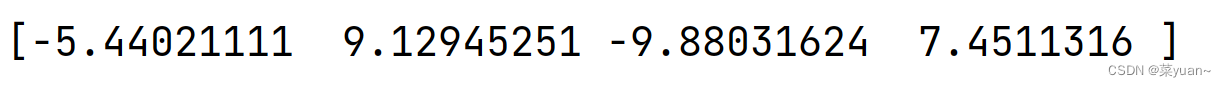
- 矩阵相乘,使用*是矩阵点乘,使用dot()方法是矩阵乘法
a = np.array([[10, 20],[30, 40]])
b = np.arange(4).reshape((2, 2))
print(a)
print(b)
c = a * b # 矩阵对应相乘,点乘
c_dot = np.dot(a, b) # 矩阵相乘
c_dot_2 = a.dot(b)
print(c)
print(c_dot)
print(c_dot_2)

- 求和运算,最大值和最小值
# 随机矩阵
a = np.random.random((2, 4))
print(a)print(np.sum(a))
print(np.max(a))
print(np.min(a))
print(np.sum(a, axis=1)) # 对每一行求和
print(np.sum(a, axis=0)) # 对每一列求和

- 完整代码
import numpy as npa = np.array([10, 20, 30, 40])
b = np.arange(4)
print(b)
# 加法
c = a + b
print(c)
# 减法
c = a - b
print(c)
# 乘方
b = b ** 2
print(b)
# 正弦
c = 10 * np.sin(a)
print(c)
# 矩阵相乘
a = np.array([[10, 20],[30, 40]])
b = np.arange(4).reshape((2, 2))
print(a)
print(b)
c = a * b # 矩阵对应相乘,点乘
c_dot = np.dot(a, b) # 矩阵相乘
c_dot_2 = a.dot(b)
print(c)
print(c_dot)
print(c_dot_2)# 随机矩阵
a = np.random.random((2, 4))
print(a)print(np.sum(a))
print(np.max(a))
print(np.min(a))
print(np.sum(a, axis=1)) # 对每一行求和
print(np.sum(a, axis=0)) # 对每一列求和
4. numpy的基础运算2
import numpy as np
A = np.arange(2, 14).reshape((3, 4))print(A)
print(np.nanargmin(A)) # 对最小值的索引
print(np.nanargmax(A)) # 对最大值的索引
print(np.mean(A)) # 平均值
print(np.median(A)) # 中位数
print(np.cumsum(A)) # 累加和
print(np.diff(A)) # 累差
print(np.nonzero(A)) # 输出非零的数的位置
print(np.sort(A)) # 逐行进行排序
print(np.transpose(A)) # 矩阵转置
print(A.T) # 矩阵转置
print((A.T).dot(A)) # 实对称矩阵
print(np.clip(A, 5, 9)) # A中小于5的数等于5,大于9的数等于9,其余不变
print(np.nanmean(A, axis=0)) # 对列进行计算平均数
print(np.nanmean(A, axis=1)) # 对行进行计算平均数
结果:
[[ 2 3 4 5][ 6 7 8 9][10 11 12 13]]
0
11
7.5
7.5
[ 2 5 9 14 20 27 35 44 54 65 77 90]
[[1 1 1][1 1 1][1 1 1]]
(array([0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2], dtype=int64), array([0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3], dtype=int64))
[[ 2 3 4 5][ 6 7 8 9][10 11 12 13]]
[[ 2 6 10][ 3 7 11][ 4 8 12][ 5 9 13]]
[[ 2 6 10][ 3 7 11][ 4 8 12][ 5 9 13]]
[[140 158 176 194][158 179 200 221][176 200 224 248][194 221 248 275]]
[[5 5 5 5][6 7 8 9][9 9 9 9]]
[6. 7. 8. 9.]
[ 3.5 7.5 11.5]
5. 索引
import numpy as np
# 一维数组
A = np.arange(3, 15)
print(A)
print(A[3]) # 对A中的值进行索引,位置是3
# 二维矩阵
A = np.arange(3, 15).reshape((3, 4))
print(A)
print(A[1]) # 对A中的值进行索引,位置是1,为第一行的数
print(A[1][1]) # 对A中第一行第一列的数进行索引
print(A[1, 1]) # 对A中第一行第一列的数进行索引
print(A[1, :]) # A中第一行的所有的数
print(A[:, 1]) # A中第一列的所有的数
print(A[1, 1:3]) # A中第一行的1-3的数,取左不取右
# 输出矩阵中每一行的数
for row in A:print(row)# 输出矩阵中每一列的数
for col in A.T:print(col)# 输出A中每一个数
print(A.flatten()) # 将矩阵转换成一维数组
for item in A.flat:print(item)
结果:
[ 3 4 5 6 7 8 9 10 11 12 13 14]
6
[[ 3 4 5 6][ 7 8 9 10][11 12 13 14]]
[ 7 8 9 10]
8
8
[ 7 8 9 10]
[ 4 8 12]
[8 9]
[3 4 5 6]
[ 7 8 9 10]
[11 12 13 14]
[ 3 7 11]
[ 4 8 12]
[ 5 9 13]
[ 6 10 14]
[ 3 4 5 6 7 8 9 10 11 12 13 14]
3
4
5
6
7
8
9
10
11
12
13
14
相关文章:

python基础知识(十三):numpy库的基本用法
目录 1. numpy的介绍2. numpy库产生矩阵2.1 numpy将列表转换成矩阵2.2 numpy创建矩阵 3. numpy的基础运算4. numpy的基础运算25. 索引 1. numpy的介绍 numpy库是numpy是python中基于数组对象的科学计算库。 2. numpy库产生矩阵 2.1 numpy将列表转换成矩阵 import numpy as …...
线程函数 tp_recv_thread() 源码分析)
【SA8295P 源码分析】16 - TouchScreen Panel (TP)线程函数 tp_recv_thread() 源码分析
【【SA8295P 源码分析】16 - TouchScreen Panel (TP)线程函数 tp_recv_thread 源码分析 一、TP 线程函数:tp_recv_thread()二、处理&上报 坐标数据 cypress_read_touch_data()系列文章汇总见:《【SA8295P 源码分析】00 - 系列文章链接汇总》 本文链接:《【SA8295P 源码…...
Python3数据分析与挖掘建模(13)复合分析-因子关分析与小结
1.因子分析 1.1 探索性因子分析 探索性因子分析(Exploratory Factor Analysis,EFA)是一种统计方法,用于分析观测变量之间的潜在结构和关联性。它旨在确定多个观测变量是否可以归结为较少数量的潜在因子,从而帮助简化…...
【stable diffusion】图片批量自动打标签、标签批量修改(BLIP、wd14)用于训练SD或者LORA模型
参考: B站教学视频【:AI绘画】新手向!Lora训练!训练集准备、tag心得、批量编辑、正则化准备】官方教程:https://github.com/darkstorm2150/sd-scripts/blob/main/docs/train_README-en.md#automatic-captioning 一、…...

TCP可靠数据传输
TCP的可靠数据传输 1.TCP保证可靠数据传输的方法 TCP主要提供了检验和、序号/确认号、超时重传、最大报文段长度、流量控制等方法实现了可靠数据传输。 检验和 通过检验和的方式,接收端可以检测出来数据是否有差错和异常,假如有差错就会直接丢失该TC…...

Python 私有变量和私有方法介绍
Python 私有变量和私有方法介绍 关于 Python 私有变量和私有方法,通常情况下,开发者可以在方法或属性名称前加上单下划线(_),以表示该方法或属性仅供内部使用,但这只是一种约定,并没有强制执行禁…...
Kotlin Lambda表达式和匿名函数的组合简直太强了
Kotlin Lambda表达式和匿名函数的组合简直太强了 简介 首先,在 Kotlin 中,函数是“第一公民”(First Class Citizen)。因此,它们可以被分配为变量的值,作为其他函数的参数传递或者函数的返回值。同样&…...

uniapp 小程序 获取手机号---通过前段获取
<template><!-- 获取手机号,登录内容 --><view><!-- 首先需要先登录获取code码,然后才可以获取用户唯一标识openid以及会话密钥及用于解密获取手机的加密信息 --><view click"login">登录</view><view…...

面板安全能力持续增强,新增日志审计功能,1Panel开源面板v1.3.0发布
2023年6月12日,现代化、开源的Linux服务器运维管理面板1Panel正式发布v1.3.0版本。 在这一版本中,1Panel进一步增强了安全方面的能力,包括新增SSH配置管理、域名绑定和IP授权支持,以及启用网站防盗链功能。此外,该版本…...
k8s学习-CKS考试必过宝典
目录 CKS考纲集群安装:10%集群强化:15%系统强化:15%微服务漏洞最小化:20%供应链安全:20%监控、日志记录和运行时安全:20% 报名模拟考试考试注意事项考前考中考后 参考 CKS考纲 集群安装:10% 使…...

jmeter如何将上一个请求的结果作为下一个请求的参数
目录 1、简介 2、用途 3、下载、简单应用 4、如何将上一个请求的结果作为下一个请求的参数 1、简介 在JMeter中,可以通过使用变量来将上一个请求的结果作为下一个请求的参数传递。 ApacheJMeter是Apache组织开发的基于Java的压力测试工具。用于对软件做压力测…...

JAVA如何学习爬虫呢?
学习Java爬虫需要掌握以下几个方面: Java基础知识:包括Java语法、面向对象编程、集合框架等。 网络编程:了解HTTP协议、Socket编程等。 HTML、CSS、JavaScript基础:了解网页的基本结构和样式,以及JavaScript的基本语…...

距离保护原理
距离保护是反映故障点至保护安装处的距离,并根据距离的远近确定动作时间的一种保护。故障点距保护安装处越近,保护的动作时间就越短,反之就越长,从而保证动作的选择性。测量故障点至保护安装处的距离,实际上就是用阻抗…...
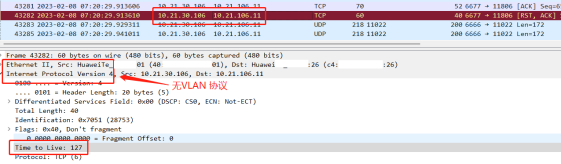
从微观世界的RST包文视角助力企业网络应用故障排查和优化
1. 前言 随着互联网的普及和发展,各行业的业务和应用越来越依赖于网络。然而,网络环境的不稳定性和复杂性使得出现各种异常现象的概率变得更高了。这些异常现象会导致业务无法正常运行,给用户带来困扰,甚至影响企业的形象和利益。…...

企业微信开发,简单测试。
企业微信开发,参考文档: https://github.com/wechat-group/WxJava/wiki...

element日期选择设置默认时间el-date-picker
<el-date-pickerv-model"rangeDate"style"width:350px"type"daterange"value-format"yyyy-MM-dd"change"dataChange"start-placeholder"开始日期"end-placeholder"结束日期"></el-date-picker…...
AB32VG:SDK_AB53XX_V061(3)IO口复用功能的补充资料
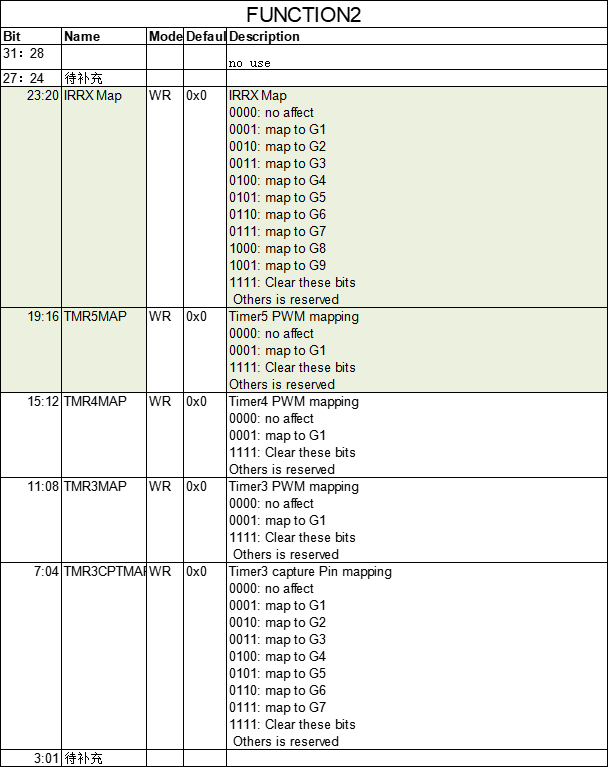
文章目录 1.IO口功能复用表格2.功能映射寄存器 FUNCTION03.功能映射寄存器 FUNCTION14.功能映射寄存器 FUNCTION2 AB5301A的官方数据手册很不完善,没有开放出来。我通过阅读源码补充了一些关于IO口功能复用寄存器的资料。 官方寄存器文档:《 AB32VG1_Re…...

UnityVR--组件10--UGUI简单介绍
目录 前言 UI基础组件 1. Canvas 2. EventSystem 3. Image 4. Text/TextMeshPro/InputField 5. Button控件 其他 前言 UGUI是Unity推出的新的UI系统,它与Unity引擎结合得更紧密,并拥有强大的屏幕自适应和更简单的深度处理机制,更容易使用和…...
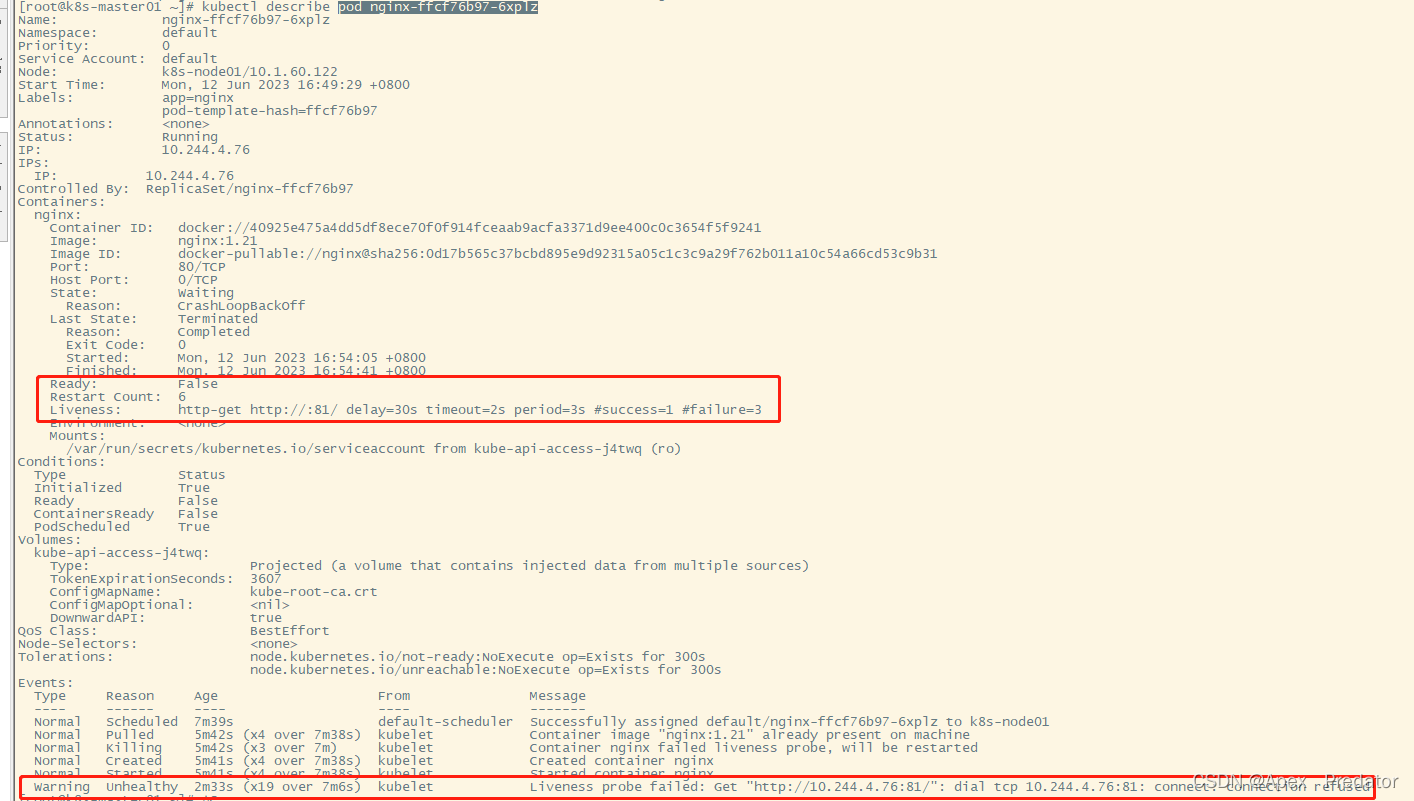
k8s 探针
1.前言 Kubernetes探针(Probe)是用于检查容器运行状况的一种机制。探针可以检查容器是否正在运行,容器是否能够正常响应请求,以及容器内部的应用程序是否正常运行等。在Kubernetes中,探针可以用于确定容器的健康状态,如果容器的健…...

【爬虫】4.4 Scrapy 爬取网站数据
目录 1. 建立 Web 网站 2. 编写 Scrapy 爬虫程序 为了说明 scrapy 爬虫爬取网站多个网页数据的过程,用 Flask 搭建一个小型的 Web 网站。 1. 建立 Web 网站 (1)books.html <!DOCTYPE html> <html lang"en"> <h…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...
