归并排序(基础+提升)
目录
归并排序的理论知识
归并排序的实现
merge函数
递归实现
递归改非递归
归并排序的性能分析
题目强化
题目一:小和问题
题目二:求数组中的大两倍数对数量
题目三:LeetCode_327. 区间和的个数
归并排序的理论知识
归并排序(Merge Sort)又叫二路归并排序,是一种基于分治法并且稳定的排序算法。它先将待排序序列递归地分成两半,对两个子序列分别递归排序,最后将已排好序的子序列利用归并操作(Merge)合并为一个整体有序的序列。归并排序的优点在于能够保证稳定性,形式上的算法复杂度为O(nlogn),适用于大数据量的排序。大体过程可以概括如下:
1. 将待排序的序列对半分为两个子序列。
2. 对两个子序列递归地调用归并排序将其变成两个有序的序列。
3. 将两个已排序的子序列合并成一个有序序列。
例如,对一个[1, 9]的区间序列进行归并排序,是先将其分为[1, 4] 和 [5, 9]两个序列,然后对这两个序列分别进行归并排序(递归的过程),最后将这两个区间进行merge(归并、合并)操作。由于是排序好的序列,所以merge起来就很方便了:先申请一个和[1, 9]范围大小相同的新序列,然后将原来的两个数组排序放入新的序列中,最后将新的序列从原数组的1位置(即左区间边界的位置)开始,覆盖到9位置(即右区间边界的位置)。
归并排序的实现
归并排序的函数定义如下:
//归并排序
class MergeSort
{
private:void merge(vector<int>&nums, int l, int mid, int r); //merge函数
public:void RecursionMerge(vector<int>& nums, int l, int r); //递归版本void IterationMerge(vector<int>& nums, int n); //迭代版本
};merge函数
merge函数的时间复杂度为O(N),由于新申请了一个数组,所以空间复杂度也是O(N)的。其中,N的大小为 r-l+1 。注意,merge函数的使用前提是要保证左右两个区间都是有序的。
void MergeSort::merge(vector<int>& nums, int l, int mid, int r)
{//边界控制if (l >= r || mid >= r)return;//先申请一个新数组vector<int> temp;int i = l, j = mid + 1;//当两个区间都没走到头的情况while (i <= mid && j <= r){int min = nums[i] < nums[j] ? nums[i++] : nums[j++];temp.push_back(min);}//当有一个区间走到头,另一个区间直接复制过去就好了//下面两个while循环一定只会执行一个while (i > mid && j <= r){temp.push_back(nums[j++]);}while (j > r && i <= mid){temp.push_back(nums[i++]);}//将新申请的数组覆盖到原数组的左区域边界lcopy(temp.begin(), temp.end(), nums.begin() + l);
}递归实现
merge函数写好之后,归并排序的递归写法就比较简单了。先递归地将左右区间归并排序,然后最后再将这两个排序好的区间序列合并起来。具体的代码实现如下:
void Sort::MergeSort::RecursionMerge(vector<int>& nums, int l, int r) //递归版本
{//base caseif (l >= r)return;//normal caseint mid = l + (r - l) / 2;RecursionMerge(nums, l, mid);RecursionMerge(nums, mid + 1, r);merge(nums, l, mid, r);
}递归改非递归
递归改非递归的核心思路就是将原来的递归过程拆分为迭代,通过手动迭代的方式模拟实现和原来递归的相同功能。
具体的做法是设一个步长step(这和希尔排序有点类似),然后以step为区间大小,划分左右区间。即从头到尾对每一个 2*step 大小的区间进行归并排序。直到走到不能以step为大小将后续区间分成左右两个区间为止,即left小于n(left是在从头到尾的过程中不断变化的)
然后从头到尾来一遍之后,使setp的值乘2,继续从头到尾来一遍,直到step的值小于待排序数组的大小n为止。具体的代码实现如下:
void MergeSort::IterationMerge(vector<int>& nums, int n)
{int step = 1;while (step < n){int left = 0;while (left < n){int mid = left + step - 1, right = min(n - 1, mid + step);merge(nums, left, mid, right);left = right + 1;}//范围检查,防止int溢出if (step >= INT_MAX / 2)break;step *= 2;}
}归并排序的性能分析
由于merge函数的时间复杂度和空间复杂度都是O(N)级别的,所以归并排序的时间复杂度为O(NlogN),空间复杂度为O(N),因为时间是不断累加的,空间是取最大的一次。
而且归并排序是三个时间复杂度O(NlogN)级别中唯一的一个有稳定性的排序,但同时也是额外空间复杂度最大的一个,(快排为O(logN),堆排是O(1)的)。
题目强化
归并排序还有一个应用场景就是对于要找一个数组中所有数的左边有多少个符合特定条件的数,可以将原本的O(N²)时间复杂度降低为O(logN)的时间复杂度。
例如:假设有这样一个数组arr:[1, 2, 3, 4, 5, 6, 7, 8]
当递归到最底层时,分组为[1, 2]、[3, 4]、[5, 6]、[7, 8]
那么此时第一组的左组为[1],右组为[2],第二组的左组为[3],右组为[4]……以此类推。
当这一次的merge结束之后,数组的分组情况为: [1, 2, 3, 4]、[5, 6, 7, 8]
那么此时第一组的左组就为[1, 2],右组为[3, 4]……
可以看到上一次的整个第一组已经变成了第二次的左组,那么将[1]作参考的话,之前的[2]是它的右组,其求的是[2]这个范围的目标值,而第二次求的就是[3. 4]这个范围的目标值。所以如果只看[1]这个数的话,从最底层的merge到最后的merge,他就是相当于分步去求了[2]~[8]这些范围的所有目标值。即其右边所有的目标值。
而对于[2]这个数,由于其第一次是做的右组,而且它永远要么是它前面数的右组,要么和前面的数一起做左组。所以同理,对于[2]这个数,从最底层的merge到最后一次merge,他也是相当于找到了[2]右边所有的目标值。
所以通过上面的过程我们可以发现,利用归并排序我们将一个数右边所有符合条件的目标值都找到了,而且每个数之间只匹配了一次,并没有赘余或者重复。
而且将原来O(N(N+1)/2)时间复杂度的任务,变成了现在O(N*logN)级别的任务。
那么如果我们想要找一个数左边所有的符合某一条件的数呢?我们可以试着用逆序排序的方式或者从在左组将原本从左往右变成内从右往左。
如果还不理解可以结合下面的题目来理解。
题目一:小和问题
题目描述:
在一个数组中,一个数左边比它小的数的总和,叫数的小和,所有数的小和累加起来,叫数组小和。求数组小和。
例子: [1,3,4,2,5]
1左边比1小的数:没有
3左边比3小的数:1
4左边比4小的数:1、3
2左边比2小的数:1
5左边比5小的数:1、3、4、 2
所以数组的小和为1+1+3+1+1+3+4+2=16
思路点拨:
由于这题是求数组的小和,并不是求每一个数组元素对应的小和。所以反正最后是求出一个和。那么我们转换思路:求数组的小和并不一定非要求出每一个数组元素左边所有比它小的数的总和。可以试着求出每一个元素所有右边比它大的数,然后数目乘自身的值,这样也是数组的小和。
我的题解:
#include <iostream>
#include <algorithm>
using namespace std;#define TEMPSIZE 5 // 数组暂定大小template <typename T>
class printVal
{
public:void operator()(T val){cout << val << " ";}
};
class lessSum // 小和问题
{/*题目描述:在一个数组中,一个数左边比它小的数的总和,叫数的小和,所有数的小和累加起来,叫数组小和。求数组小和。例子:[1,3,4,2,5]1左边比1小的数:没有3左边比3小的数:14左边比4小的数:1、32左边比2小的数:15左边比5小的数:1、3、4、 2所以数组的小和为1+1+3+1+1+3+4+2=16思路分析:由于这题是求数组的小和,并不是求每一个数组元素对应的小和。所以反正最后是求出一个和。那么我们转换思路,求数组的小和并不一定非要求出每一个数组元素左边所有比它小的数的总和。可以试着求出每一个元素所有右边比它大的数,然后数目乘自身的值,这样也是数组的小和。*/
private:void base_merge(int *nums, int l, int m, int r); // 将l ~ m与m+1 ~ r范围的有序数组合并int merge(int *nums, int l, int m, int r);public:void mergeSortMode(int *nums, int n);int solution(int *nums, int l, int r);
};int main()
{int nums[TEMPSIZE] = {1, 3, 4, 2, 5};// lessSum().mergeSortMode(nums, 5);cout << lessSum().solution(nums, 0, 4) << endl;for_each(nums, nums + TEMPSIZE, printVal<int>());return 0;
}void lessSum::mergeSortMode(int *nums, int n)
{int step = 1;while (step < n){int mid = 0, left = 0, right = 0;while (left < n){mid = left + step - 1, right = std::min(mid + step, n - 1);merge(nums, left, mid, right);left = right + 1;}step *= 2;}
}
int lessSum::solution(int *nums, int l, int r)
{if (l >= r)return 0;int mid = l + (r - l) / 2;return solution(nums, l, mid) + solution(nums, mid + 1, r) + merge(nums, l, mid, r);
}
int lessSum::merge(int *nums, int l, int mid, int r)
{if (l >= r)return 0;int ans = 0, n = r - l + 1;int tmp[TEMPSIZE] = {0}, index = 0;int i = l, j = mid + 1; // i-左组区域,j-右组区域while (i <= mid && j <= r){//要保持i位置严格小于j位置,因为要保证先拷贝右组数据ans += nums[i] < nums[j] ? nums[i] * (r - j + 1) : 0;tmp[index++] = nums[i] < nums[j] ? nums[i++] : nums[j++];}if (i == mid + 1){copy(nums + j, nums + r + 1, tmp + index);}if (j == r + 1){copy(nums + i, nums + mid + 1, tmp + index);}copy(tmp, tmp + n, nums + l);cout << l << " " << r <<" "<< ans << endl;return ans;
}
void lessSum::base_merge(int *nums, int l, int m, int r)
{if (l >= r)return;int size = r - l + 1;int tmp[TEMPSIZE] = {0};int i = l, j = m + 1, index = 0;while (i <= m && j <= r)tmp[index++] = nums[i] < nums[j] ? nums[i++] : nums[j++];if (i == m + 1)copy(nums + j, nums + r + 1, tmp + index);if (j == r + 1)copy(nums + i, nums + m + 1, tmp + index);copy(tmp, tmp + size, nums + l);
}题目二:求数组中的大两倍数对数量
题目描述:
求给定数组中特定的元素的对数。
特定元素-在num的右边有多少个数,它的二倍还没有num大。返回总对数。
思路点拨:
我们假定归并排序是按照升序排的,那么每次merge的时候左右组中的数据都是升序排序好的,所以我们找count的时候就不用一个一个数了,如果右组right中的当前数还没有当前左组的数left大,那么在right之前的数的二倍也一定都没有left大,所以此时的count值就可以直接加上一个 右组的大小size - 右组当前位置right的下标。
我的题解:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;class solution
{
private:int merge(vector<int> &nums, int l, int mid, int r);public:int mytry(vector<int> &nums, int l, int r){if (l >= r)return 0;int mid = l + (r - l) / 2;int left = mytry(nums, l, mid);int right = mytry(nums, mid + 1, r);int now = merge(nums, l, mid, r);return left + right + now;}
};
int solution::merge(vector<int> &nums, int l, int mid, int r)
{if (l >= r)return 0;int edgeR = mid + 1, count = 0;//枚举求countfor (int i = l; i <= mid; i++){while (edgeR <= r && nums[i] <= nums[edgeR] * 2 && edgeR++);count += r - edgeR + 1;}// 归并部分vector<int> tmp;int i = l, j = mid + 1;while (i <= mid && j <= r){tmp.push_back(nums[i] > nums[j] ? nums[i++] : nums[j++]);}while (i > mid && j <= r)tmp.push_back(nums[j++]);while (j > r && i <= mid)tmp.push_back(nums[i++]);copy(tmp.begin(), tmp.end(), nums.begin() + l);//返回countreturn count;
}
int main()
{// 数据:[6, 7, 3, 2, 1] ans:6vector<int> nums = {6, 7, 2, 3, 1};cout << solution().mytry(nums, 0, nums.size() - 1) << endl;return 0;
}题目三:LeetCode_327. 区间和的个数
题目描述:
给你一个整数数组 nums 以及两个整数 lower 和 upper 。求数组中,值位于范围 [lower, upper] (包含 lower 和 upper)之内的 区间和的个数 。
区间和 S(i, j) 表示在 nums 中,位置从 i 到 j 的元素之和,包含 i 和 j (i ≤ j)。
示例 1:
输入:nums = [-2,5,-1], lower = -2, upper = 2
输出:3
解释:存在三个区间:[0,0]、[2,2] 和 [0,2] ,对应的区间和分别是:-2 、-1 、2 。
示例 2:输入:nums = [0], lower = 0, upper = 0
输出:1
提示:
1 <= nums.length <= 105
-231 <= nums[i] <= 231 - 1
-105 <= lower <= upper <= 105
题目数据保证答案是一个 32 位 的整数来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/count-of-range-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路点拨:
首先,我们假定从 i 到 j 范围的区间和表示为 S(i, j),那么S(i, j)就可以等价转换为 S(i, j) = S(0, j) - S(0, i) ,所以我们可以搞一个前缀和数组Sum,数组中每一个元素对应的就是当前的S(0, index)。
那么如果S(i, j)的范围是 [lower, upper]的话,就表示Sum[j] - Sum[i]的范围就是 [lower, upper],即 lower <= Sum[j] - Sum[i] <= upper,那么转换一下就是 Sum[j] - upper <= Sum[i] <= Sum[j] - lower ,这就表示在Sum数组中,如果当前位置为 j ,对应的前缀和为Sum[j],那么就相当于在Sum数组中找在 j 的左边有多少Sum[i]符合 Sum[j] - upper <= Sum[i] <= Sum[j] - lower。
到了这里就对上了,“找一个数左边所有符合条件数的个数”的情形,只不过这里我们需要将原数组处理成前缀和数组Sum,然后对这个Sum数组进行操作,而不是对原数组进行操作。
我的题解:
#include<iostream>
#include<vector>
#include<string>
#include<list>
#include<algorithm>
using namespace std;class Solution
{
public:int merge(vector<long>& sum, int l, int mid, int r, int lower, int upper){// 由于左组和右组都是有序的,所以巧妙的实现了指针不用回退// 这里的i对应“思路点拨”部分的jint cnt = 0;int l_edge = l, r_edge = l; for (int i = mid + 1; i <= r; i++){long tagL = sum[i] - upper, tagR = sum[i] - lower;while (sum[r_edge] <= tagR && r_edge <= mid) // 走到第一个大于tagR的位置r_edge++;while (sum[l_edge] < tagL && l_edge <= mid) // 走到第一个不小于tagL的位置l_edge++;//由于r_edge是在第一个大于tagR的位置,所以sum的区间为(L,R],故最终减去l_edge的结果就不用再+1了cnt += r_edge - l_edge > 0 ? r_edge - l_edge : 0; }// 正常的mergevector<long> temp;int i = l, j = mid + 1;while (i <= mid && j <= r){temp.push_back(sum[i] < sum[j] ? sum[i++] : sum[j++]);}while (i > mid && j <= r){temp.push_back(sum[j++]);}while (j > r && i <= mid){temp.push_back(sum[i++]);}copy(temp.begin(), temp.end(), sum.begin() + l);// 返回当前区间值位于范围 [lower, upper] 的区间和return cnt;}int sumCount(vector<long>& sum, int l, int r, int lower, int upper){if (l == r)return sum[l] >= lower && sum[r] <= upper;int mid = (l + r) / 2;return sumCount(sum, l, mid, lower, upper) +sumCount(sum, mid + 1, r, lower, upper) + merge(sum, l, mid, r, lower, upper);}int countRangeSum(vector<int>& nums, int lower, int upper){// 填充sum序列,其中S(i,j) = S(0,j) - S(0,i) vector<long> sum; // sum数组,比nums大1sum.push_back(nums[0]);for (int i = 1; i < nums.size(); i++){sum.push_back(sum[i - 1] + nums[i]);}//返回符合条件区间和的数量return sumCount(sum, 0, sum.size() - 1, lower, upper);}
};int main()
{auto pt = [](const int val){ cout << val << " "; };vector<int> nums = { -2, 5, -1 };for_each(nums.begin(), nums.end(), pt);cout << endl;cout << Solution().countRangeSum(nums, -2, 2);return 0;
}相关文章:
)
归并排序(基础+提升)
目录 归并排序的理论知识 归并排序的实现 merge函数 递归实现 递归改非递归 归并排序的性能分析 题目强化 题目一:小和问题 题目二:求数组中的大两倍数对数量 题目三:LeetCode_327. 区间和的个数 归并排序的理论知识 归并排序&…...

MATLAB应用
目录 网站 智能图像色彩缩减和量化 网站 https://yarpiz.com/ 智能图像色彩缩减和量化 使用智能聚类方法:(a)k均值算法,(b)模糊c均值聚类(FCM)和(c)自组织神…...

LeetCode --- 1784. Check if Binary String Has at Most One Segment of Ones 解题报告
Given a binary string s without leading zeros, return true if s contains at most one contiguous segment of ones. Otherwise, return false. Example 1: Input: s = "1001" Output: false Explanation: The ones do not form a contiguous s…...

js:javascript中的事件体系:常见事件、事件监听、事件移除、事件冒泡、事件捕获、事件委托、阻止事件
参考资料 事件介绍Element事件 目录 常见的事件鼠标事件键盘事件Focus events 添加事件监听方式一:addEventListener()(推荐)方式二:事件处理器属性方式三:内联事件处理器(不推荐) 移除监听器方…...

【数据结构】特殊矩阵的压缩存储
🎇【数据结构】特殊矩阵的压缩存储🎇 🌈 自在飞花轻似梦,无边丝雨细如愁 🌈 🌟 正式开始学习数据结构啦~此专栏作为学习过程中的记录🌟 文章目录 🎇【数据结构】特殊矩阵的压缩存储Ἰ…...

在layui中使用vue,使用vue进行页面数据部分数据更新
layui是一款非常优秀的框架,使用也非常的广泛,许多后台管理系统都使用layui,简单便捷,但是在涉及页面部分数据变化,就比较难以处理,比如一个页面一个提交页,提交之后部分数据实时进行更新&#…...

Vue中如何进行数据导入与Excel导入
Vue中如何进行数据导入与Excel导入 Vue是一款非常流行的JavaScript框架,它提供了一套用于构建用户界面的工具和库。在Vue中,我们可以使用多种方式来导入数据,包括从服务器获取数据、从本地存储获取数据、从文件中读取数据等等。其中…...

git 的基本操作
1. git建立本地仓库 在想要建立的目录下输入命令 git init 我们可以看一下 .git目录下有什么 2. 配置git本地仓库 配置用户的 name 和 email 命令:git config [...] 配置完后,我们像查看一下 刚才的配置 2.1 查看配置命令 git config -l 2.2 删除…...
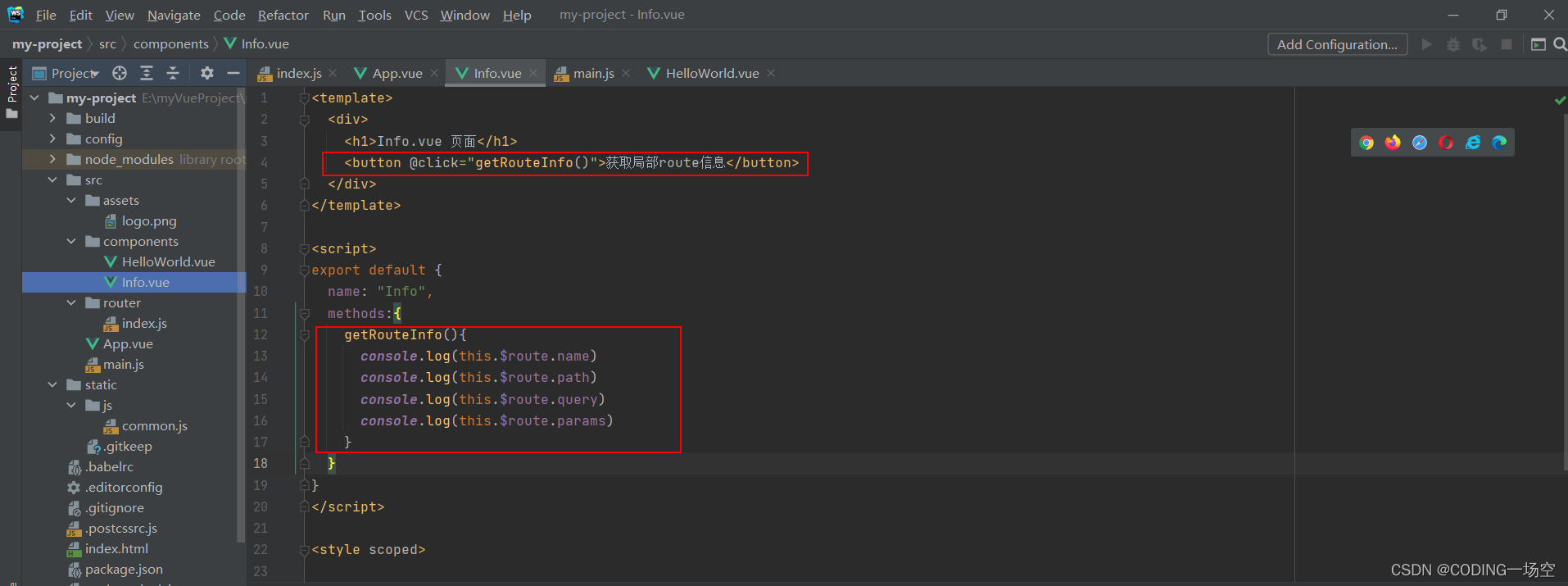
搭建Vue项目以及项目的常见知识
前言:使用脚手架搭建vue项目,使用脚手架可以开发者能够开箱即用快速地进行应用开发而开发。 搭建 #创建一个基于 webpack 模板的新项目 vue init webpack my-project #选择所需要的选项如图: cd my-project npm run dev访问localhost:808…...

TypeScript ~ TS Webpack构建工具 ⑦
作者 : SYFStrive 博客首页 : HomePage 📜: TypeScript ~ TS 📌:个人社区(欢迎大佬们加入) 👉:社区链接🔗 📌:觉得文章不错可以点点关注 &…...

Rust 自建HTTP Server支持图片响应
本博客是在杨旭老师的 rust web 全栈教程项目基础上进行修改,支持了图片资源返回,杨旭老师的rust web链接如下: https://www.bilibili.com/video/BV1RP4y1G7KFp1&vd_source8595fbbf160cc11a0cc07cadacf22951 本人默认读者已经学习了相关…...

[游戏开发][Unity]UnityWebRequest使用大全
首先记录个小问题 使用new UnityWebRequest的方式,最终的downloadHandler是个null 使用UnityWebRequest.Get的方式,最终的downloadHandler会是DownloadHandlerBuffer 从网站或本地下载内容,包括文本或二进制数据 IEnumerator downloadfile(st…...
如何使用Fiddler对手机进行弱网测试?(干货教程)
1.首先,fiddler连接手机 1)Tools->Options->Connections->设置端口8888,勾选Allow remote computers to connect 2)配置手机 注:手机和电脑需要在同一局域网下 手机进入网络详情,将代理改为手动 设置主机名、端口 主机…...

专业科普:什么是单片机?
一、什么是单片机 单片机诞生于20世纪70年代末,它是指一个集成在一块芯片上的完整计算机系统。单片机具有一个完整计算机所需要的大部分部件:CPU、内存、内部和外部总线系统,目前大部分还会具有外存。同时集成诸如通讯接口、定时器ÿ…...

深度学习-第T11周——优化器对比实验
深度学习-第T11周——优化器对比实验 深度学习-第T11周——优化器对比实验一、前言二、我的环境三、前期工作1、导入数据集2、查看图片数目3、查看数据 四、数据预处理1、 加载数据1、设置图片格式2、划分训练集3、划分验证集4、查看标签 2、数据可视化3、检查数据4、配置数据集…...
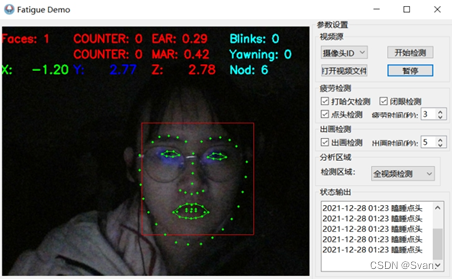
基于Dlib的疲劳检测系统
需要源码的朋友可以私信我 基于Dlib的疲劳检测系统 1、设计背景及要求2、系统分析3、系统设计3.1功能结构图3.2基于EAR、MAR和HPE算法的疲劳检测3.2.1基于EAR算法的眨眼检测3.2.2基于MAR算法的哈欠检测3.3.3基于HPE算法的点头检测 4、系统实现与调试4.1初步实现4.2具体实现过程…...

three.js通过CubeTexture加载环境贴图,和RGBELoader加载器加载hdr环境贴图
一、使用CubeTexture进行环境贴图 1.CubeTexture使用介绍 Three.js中可以通过使用CubeTexture进行环境贴图,CubeTexture需要将6张图片(正面、反面、上下左右)包装成一个立方体纹理。下面是一个简单的例子: 首先需要加载六张贴图…...
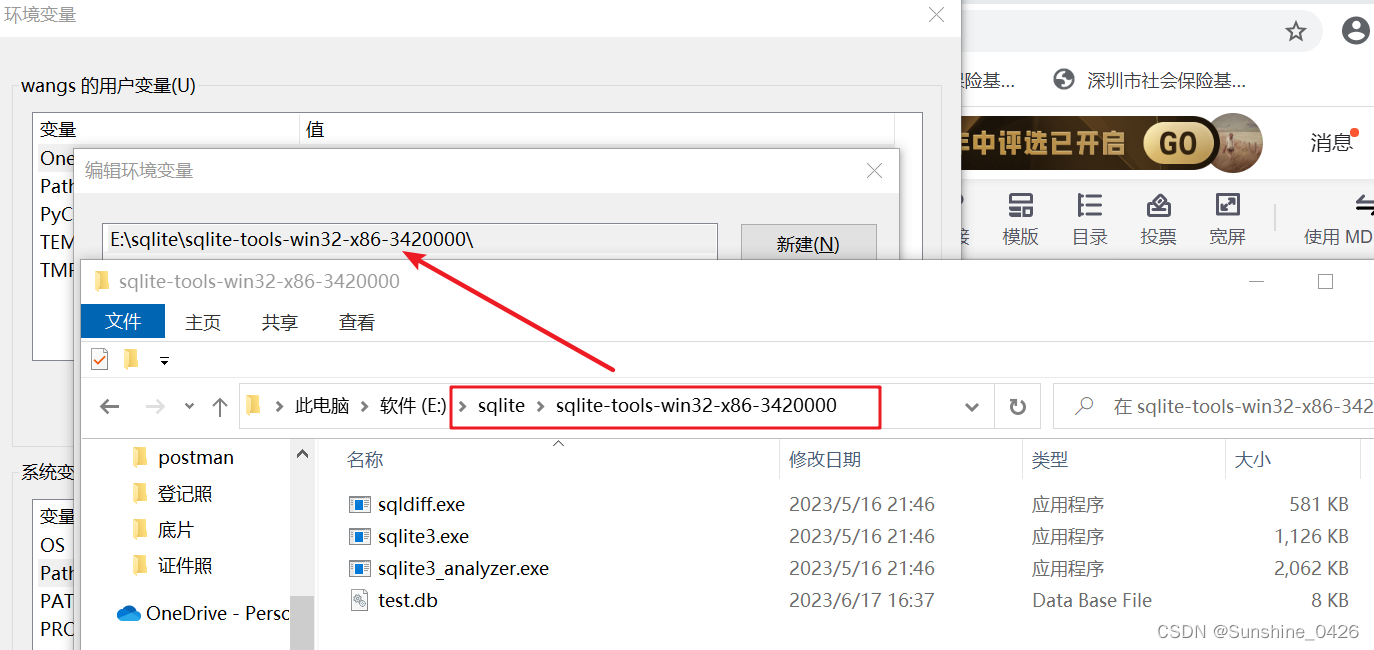
pycharm中Terminal输入sqlite3,出现无法将sqlite项识别为cmdlet**的解决方法
前提:本机上已安装sqlite3,安装详见:pycharm社区版中安装配置sqlite3_Sunshine_0426的博客-CSDN博客 问题: cmd命令行中或pycharm中Terminal行输入sqlite3 db.sqlite3命令后,出现“无法将“sqlite3”项识别为 cmdlet…...
VSCode 安装配置教程详解包含c++环境配置方法
vscode安装教程及c环境配置详解 vscode下载安装下载C扩展插件VScode C环境配置配置环境变量检查 MinGW 安装配置编译器:配置构建任务检查是否安装了编译器配置完毕 vscode下载安装 地址:官网下载地址 直接打开下载好的.exe文件进行安装即可࿰…...
)
Baumer工业相机堡盟工业相机如何通过BGAPISDK将图像放大缩小显示(C#)
Baumer工业相机堡盟工业相机如何通过BGAPISDK将图像放大缩小显示(C#) Baumer工业相机Baumer工业相机BGAPISDK和图像放大缩小的技术背景Baumer工业相机通过BGAPISDK将相机图像图像放大缩小功能1.引用合适的类文件2.通过BGAPISDK将相机图像图像放大缩小功能…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
