CUDA编程模型系列八(原子操作 / 规约 / 向量元素求和)
本系列视频目的是帮助开发者们一步步地学会利用CUDA编程模型加速GPU应用, 我们的口号是: 让GPU飞起来
本期我介绍了cuda 当中规约算法的一种情况, 也是小何尚职业生涯中的第一道面试题, 计算数组中所有元素的和.
CUDA编程模型系列八(原子操作 / 规约 / 向量元素求和)
#include <stdio.h>
#include <math.h>#define N 100000000
#define BLOCK_SIZE 256
#define GRID_SIZE 32__managed__ int source[N];
__managed__ int gpu_result[1] = {0};// source[N]: 1 + 2 + 3 + 4 + ...............N
// cpu: for loop
// gpu: 1 + 2 + 3 + 4 + ...............N 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 8 9 10 11 12 .... 31
// thread id step 0: tid0:source[0] + source[4] -> source[0]
// tid1:source[1] + source[5] -> source[1]
// tid2:source[2] + source[6] -> source[2]
// tid4:source[4] + source[7] -> source[3]
// step 1: tid0: source[0] + source[2] -> source[0]
// tid1: source[1] + source[3] -> source[1]
//
// step 2: tid0: source[0] + source[1] -> source[0]
// thread id: blockDim.x * blockIdx.x + threadIdx.x + step * blockDim.x * GridDim.x
// thread 0: source[0, 8, 16, 24] sum -> shared memory
//
//__global__ void sum_gpu(int *in, int count, int *out)
{__shared__ int ken[BLOCK_SIZE];//grid_loopint shared_tmp=0;for(int idx = blockDim.x * blockIdx.x + threadIdx.x; idx < count; idx += blockDim.x * gridDim.x){shared_tmp +=in[idx];}ken[threadIdx.x] = shared_tmp;__syncthreads();int tmp =0;for(int total_threads = BLOCK_SIZE/2; total_threads>=1; total_threads/=2){if(threadIdx.x < total_threads){tmp = ken[threadIdx.x] + ken[threadIdx.x + total_threads]; }__syncthreads();if(threadIdx.x < total_threads){ken[threadIdx.x] = tmp;}}// block_sum -> share memory[0]if(blockIdx.x * blockDim.x < count){if(threadIdx.x == 0){atomicAdd(out, ken[0]);// memory space wmr}}}int main()
{int cpu_result =0;printf("Init input source[N]\n");for(int i =0; i<N; i++){source[i] = rand()%10;}cudaEvent_t start, stop_cpu, stop_gpu;cudaEventCreate(&start);cudaEventCreate(&stop_cpu);cudaEventCreate(&stop_gpu);cudaEventRecord(start);cudaEventSynchronize(start);for(int i = 0; i<20; i++){gpu_result[0] = 0;sum_gpu<<<GRID_SIZE, BLOCK_SIZE>>>(source, N, gpu_result);cudaDeviceSynchronize();}cudaEventRecord(stop_gpu);cudaEventSynchronize(stop_gpu);for(int i =0; i<N; i++){cpu_result +=source[i];}cudaEventRecord(stop_cpu);cudaEventSynchronize(stop_cpu);float time_cpu, time_gpu;cudaEventElapsedTime(&time_cpu, stop_gpu, stop_cpu);cudaEventElapsedTime(&time_gpu, start, stop_gpu);printf("CPU time: %.2f\nGPU time: %.2f\n", time_cpu, time_gpu/20);printf("Result: %s\nGPU_result: %d;\nCPU_result: %d;\n", (gpu_result[0] == cpu_result)?"Pass":"Error", gpu_result[0], cpu_result);return 0;
}相关文章:
)
CUDA编程模型系列八(原子操作 / 规约 / 向量元素求和)
本系列视频目的是帮助开发者们一步步地学会利用CUDA编程模型加速GPU应用, 我们的口号是: 让GPU飞起来 本期我介绍了cuda 当中规约算法的一种情况, 也是小何尚职业生涯中的第一道面试题, 计算数组中所有元素的和. CUDA编程模型系列八(原子操作 / 规约 / 向量元素求和) #include…...
)
go语言系列基础教程总结(4)
1、goroutine和channel 每执行一次go func()就创建一个 goroutine,包含要执行的函数和上下文信息。 goroutine 是Go程序并发的执行体,channel是它们之间的沟通连接通道。 var ch1 chan int. //声明一个整型的通道 2、channel 常用操作 //定义一个…...
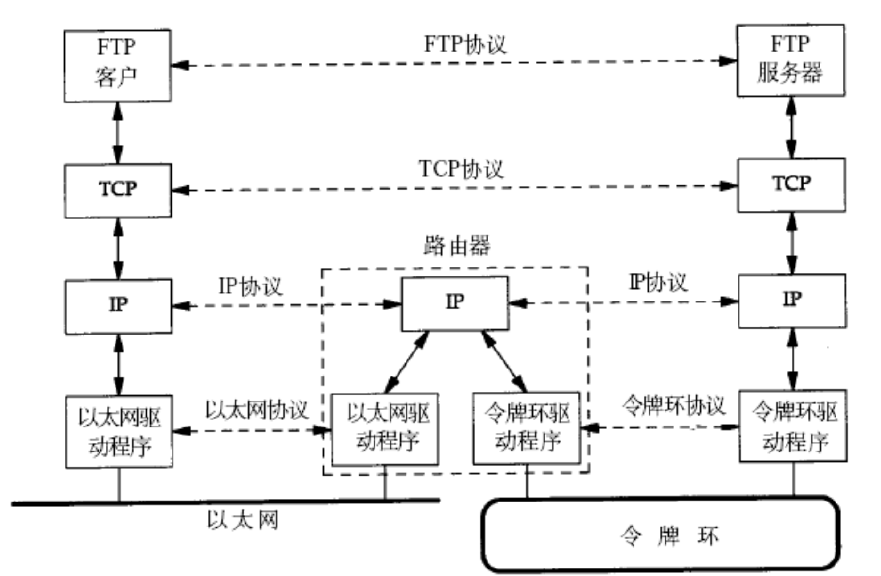
网络基础一:网络协议初识与网络传输基本流程
目录 网络协议认识“协议”网络协议初识协议分层OSI七层模型(理论模型)TCP/IP五层(或四层)模型(工程实现模型) 网络中的地址管理MAC地址IP地址 网络传输基本流程路由的本质 数据包封装和分用网络协议需要解决的问题 网络协议 计算…...

Mysql找出执行慢的SQL【慢查询日志使用与分析】
分析慢SQL的步骤 慢查询的开启并捕获:开启慢查询日志,设置阈值,比如超过5秒钟的就是慢SQL,至少跑1天,看看生产的慢SQL情况,并将它抓取出来explain 慢SQL分析show Profile。(比explain还要详细…...
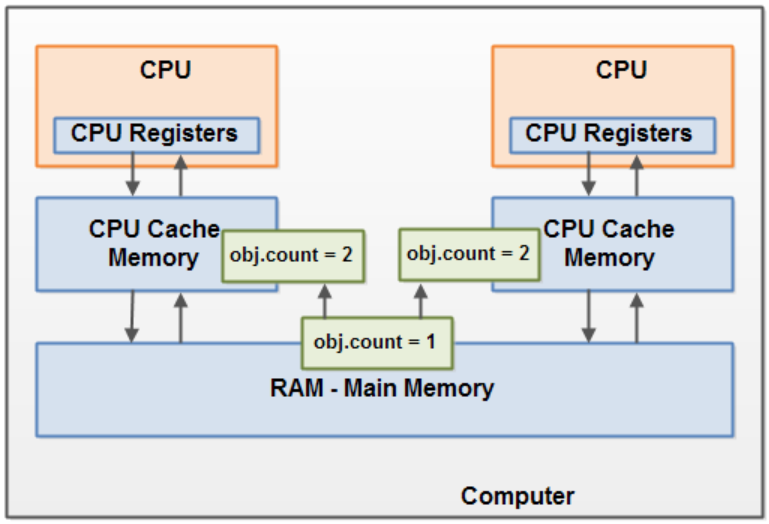
设计模式3:单例模式:JMM与volatile和synchronized的关系
本文目录 JMM简介Java 内部内存模型(The Internal Java Memory Model)硬件内存架构(Hardware Memory Architecture)弥合 Java 内存模型和硬件内存架构之间的差距(Bridging The Gap Between The Java Memory Model And The Hardware Memory Architecture)1.共享对象的可见性2.竞…...
)
一个简单的OPC UA/ModbusTCP 网关(Python)
使用我前面几篇博文的内容,能够使用Python编写一个最简单的OPC UA /ModbusTCP网关。 从这个程序可以看出: 应用OPC UA 并不难,现在我们就可以应用到工程应用中,甚至DIY项目也可以。不必采用复杂的工具软件。使用Python 来构建工…...
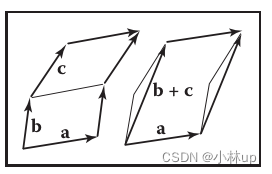
线性代数行列式的几何含义
行列式可以看做是一系列列向量的排列,并且每个列向量的分量可以理解为其对应标准正交基下的坐标。 行列式有非常直观的几何意义,例如: 二维行列式按列向量排列依次是 a \mathbf{a} a和 b \mathbf{b} b,可以表示 a \mathbf{a} a和…...

python用flask将视频显示在网页上
注意我们的return返回值必须是以下之一,否则会报错 from flask import Flask, render_template, Response import cv2app Flask(__name__)app.route(/) def index():return render_template(index.html)def gen(camera):while True:success, image camera.read(…...
【数据挖掘】时间序列教程【一】
第一章 说明 对于时间序列的研究,可以追溯到19世纪末和20世纪初。当时,许多学者开始对时间相关的经济和社会现象进行研究,尝试发现其规律和趋势。其中最早的时间序列研究可以追溯到法国经济学家易贝尔(Maurice Allais)…...

优化索引粒度参数提升ClickHouse查询性能
当对高基数列进行过滤查询时,总是希望尽可能跳过更多的行。否则需要处理更多数据、需要更多资源。ClickHouse缺省在MergeTree表读取8192行数据块,但我们可以在创建表时调整该index_granularity 参数。本文通过示例说明如何调整该参数优化查询性能。 inde…...

selenium\webdriver\remote\errorhandler.py:242: SessionNotCreatedException问题解决
报错信息: raise exception_class(message, screen, stacktrace) E selenium.common.exceptions.SessionNotCreatedException: Message: session not created: This version of ChromeDriver only supports Chrome version 112 E Current browser versi…...
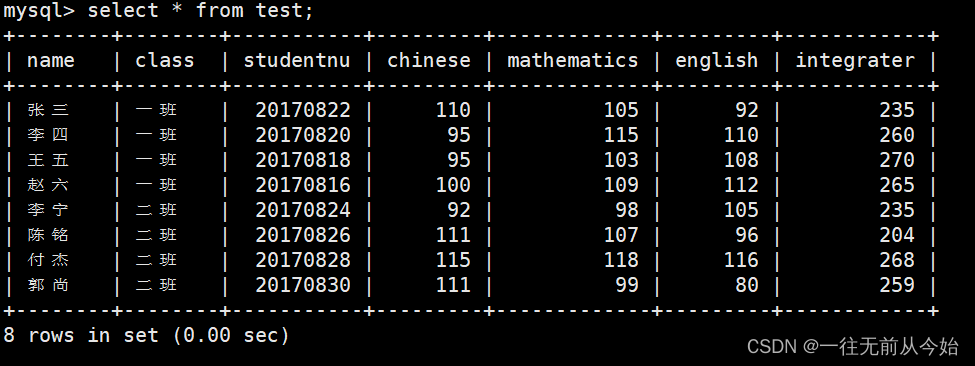
MySQL 备份与恢复
MySQL 备份与恢复 一、数据库备份的分类1.1 数据备份的重要性1.2 数据库备份的分类1.2.1 从物理与逻辑的角度,分为物理备份和逻辑备份1.2.2 从数据库的备份策略角度,分为完全备份,差异备份和增量备份1.2.3 常见的备份方法 二、MySQL完全备份与…...
js中改变this指向的三种方式
js中改变this指向的三种方式 1、call方法2、apply方法3、bind方法 1、call方法 使用 call 方法调用函数,同时指定函数中 this 的值,使用方法如下代码所示: <script>const obj {uname: 刘德华}function fn(x, y) {console.log(this) …...

小程序中如何进行数据传递和通信
103. 小程序中如何进行数据传递和通信? 1. 使用页面参数传递数据: 在小程序中,可以通过页面参数来传递数据。当跳转到一个新页面时,可以将需要传递的数据作为参数传入,然后在目标页面的onLoad函数中获取参数。 示例…...
Vue3项目中引入ElementUI使用详解
目录 Vue3项目中引入 ElementUI1.安装2.引入2.1 全局引入2.2 按需引入viteWebpack 3.使用 Vue3项目中引入 ElementUI ElementUI是一个强大的PC端UI组件框架,它不依赖于vue,但是却是当前和vue配合做项目开发的一个比较好的ui框架,其包含了布局…...

计算机启动
按下主机上的 power 键后,第一个运行的软件是 BIOS,BIOS 全称叫 Base Input & Output System,即基本输入输出系统。 (8086的1MB内存) 地址 0~0x9FFFF 处是 DRAM,顶部的 0xF0000~0xFFFFF&am…...
Unity学习笔记--EventSystem事件系统在使用上需要注意的地方(很基础,但是很多人会忘记!!!)
目录 前言代码Unity 场景配置运行报错分析解决办法拓展(预告) 前言 之前有写过一篇关于事件系统实现以及使用的文章 Unity学习笔记–C#事件系统的实现与应用 最近在使用的时候遇到了一些问题,所以在此记录下,也为看到这篇文章的人…...

高手必备:JVM调优的常用命令和参数一网打尽!
大家好,我是小米!在今天的技术分享中,我将和大家一起探讨JVM调优中的常用命令和参数。作为一名热爱技术的小伙伴,希望通过本篇文章的分享,能够帮助大家更好地理解和掌握JVM调优的方法和技巧。 JVM的结构 首先&#x…...

Uniapp 开发 ①(快速上手)
作者 : SYFStrive 博客首页 : HomePage 📜: UNIAPP开发 📌:个人社区(欢迎大佬们加入) 👉:社区链接🔗 📌:觉得文章不错可以点点关注 Ǵ…...

【数据库原理与实践】知识点归纳(下)
第6章 规范化理论 一、关系模式设计中存在的问题 关系、关系模式、关系数据库、关系数据库的模式 关系模式看作三元组:R < U,F >,当且仅当U上的一个关系r满足F时,r称为关系模式R < U,F >的一个关系 第一范式(1NF&…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
