【数据结构与算法篇】之时间复杂度与空间复杂度
【数据结构与算法篇】之时间复杂度与空间复杂度
- 一、时间复杂度
- 1.1时间复杂度的定义
- 1.2 常见的时间复杂度的计算
- 1.3 常见的函数的时间复杂度
- 二、空间复杂度

❤️博客主页: 小镇敲码人
🍏 欢迎关注:👍点赞 👂🏽留言 😍收藏
🌞友友们暑假快乐,好久不见呀!!!💖💖💖
🍉 有人曾经问过我这样一个问题,“人终其一身,执着追求的东西究竟是什么?”我是这样回答的,”我们终其一生都在寻找着那个和我们灵魂极其契合的人,可最后才发现,那个人只有也只能是自己,学会在无聊时消遣自己是非常重要的“,所以无论目前屏幕上的你深处怎样的绝境之中,请不要放弃自己,好好的爱自己就是度过绝境的最佳武器!!!😸😸😸
一、时间复杂度
1.1时间复杂度的定义
在计算机与科学中,算法的时间复杂度(time complexity)是一个函数,它定性的描述算法的运行时间,表示一个程序来回执行的次数,但不定量。这个函数的自变量是算法输入值的字符串的长度,即 N N N。时间复杂度常用大O符号表述,只包括那个幂次最高的项数。使用这种方式时,时间复杂度可被称为是渐近的,也就是 lim N → ∞ O ( N ) \lim\limits_{N\rarr\infin}O(N) N→∞limO(N)时的情况。例如,如果一个算法对于任何大小为 N N N的输入,它至多需要 5 N 3 N^3 N3 + 3 N 3N 3N 的时间运行完毕,那么它的渐近时间复杂度是 O ( N 3 ) O(N^3) O(N3)。
- 注意:时间复杂度不计算时间,只计算程序的执行次数。
常见的时间复杂度包括:
- 常数时间复杂度( O ( 1 ) ) O(1)) O(1)):算法的执行时间与输入规模无关,常数级别的执行时间。
- 线性时间复杂度( O ( N ) O(N) O(N)):算法的执行时间与输入规模线性相关,随着输入规模的增加而线性增长。
- 对数时间复杂度( O ( l o g N ) O(log N) O(logN)):算法的执行时间与输入规模的对数关系,通常是二分查找等算法的时间复杂度。
- 平方时间复杂度( O ( N 2 ) O(N^2) O(N2)):算法的执行时间与输入规模的平方相关,通常是嵌套循环等算法的时间复杂度。
- 线性对数时间复杂度 ( O ( N ∗ l o g N ) ) (O(N*log N)) (O(N∗logN)) :它表示随着输入规模 N 的增加,算法的执行时间以 N 乘以 log N 的速度增长,线性对数时间复杂度常常出现在一些高效的排序算法(如快速排序和归并排序)以及一些分治算法中。
注意:嵌套循环的算法时间复杂度不一定是 O ( N 2 ) O(N^2) O(N2)。
通过分析算法的时间复杂度,我们可以更好地理解算法的性能特点,并进行算法的选择和优化。
1.2 常见的时间复杂度的计算
1.2.1 常数时间复杂度( O ( 1 ) ) O(1)) O(1))
int main(){int a = 0;a += 1;printf("%d",&a);return 0;}
这段代码执行了四次操作。我们逐行分析代码的执行过程:
1.int a = 0;:这行代码初始化了整数变量a,将其赋值为 0。
2. a += 1;:这行代码将变量 a的值增加 1,现在 a 的值为 1。
3.printf("%d", &a);:这行代码使用 printf 函数打印变量 a 的值的内存地址,格式化输出为十进制整数。
4. return 0;:在 main 函数的结尾,使用 return 语句将返回值设为 0。
因此,代码执行了四次操作。
- 若对于一个算法 T ( n ) T(n) T(n)的上界与输入大小无关,则称其具有常数时间,记作O(1)时间,故而这个算法的时间复杂度为 O ( 1 ) O(1) O(1)。
1.2.2 线性时间复杂度( O ( N ) O(N) O(N))
int main()
{int n = 0;scanf("%d",&n);int sum = 1;for(int i = 1;i < n;;i++)sum *= i;printf("%d",sum);return 0;
}
这段代码的执行过程如下:
int n = 0;:这行代码声明了一个整数变量 n,并将其初始化为 0。scanf("%d",&n);:这行代码使用 scanf 函数从标准输入中读取一个整数,并将其赋值给变量 n。int sum = 1;:这行代码声明了一个整数变量 sum,并将其初始化为 1。for(int i = 1;i < n;i++):这行代码开始一个 for 循环,循环变量 i 的初始值为 1,循环条件为 i < n。sum *= i;:这行代码将变量 sum 与变量 i 相乘,并将结果赋值给 sum。printf("%d",sum);:这行代码使用 printf 函数打印变量 sum 的值。return 0;:在 main 函数的结尾,使用 return 语句将返回值设为 0。- 在
for循环中,变量 i 的初始值为 1,每次循环 i 的值递增 1,直到达到 n 的值。因此,for 循环的执行次数为 n - 1。在循环中,执行了一次乘法操作 sum *= i,共执行了 n - 1 次。
- 故而程序的执行次数为: T ( N ) = 5 + 2 ∗ ( N − 1 ) = 2 N + 3 , T(N)=5+2*(N-1)=2N+3, T(N)=5+2∗(N−1)=2N+3, lim N → ∞ T ( N ) = O ( N ) \lim\limits_{N\rarr\infin}T(N)=O(N) N→∞limT(N)=O(N)。
1.2.3 对数时间复杂度( O ( l o g N ) O(log N) O(logN))
#include <stdio.h>void logarithmicAlgorithm(int n) {int i = 1;while (i < n) {printf("%d\n", i);i *= 2; // 对数时间复杂度的关键步骤}
}int main() {int n = 16;logarithmicAlgorithm(n);return 0;
}
这段代码的执行过程如下:
- 在
main函数中,声明一个整数变量 n 并赋值为 16。- 调用
logarithmicAlgorithm()函数,并将变量 n 作为参数传递给该函数。- 进入
logarithmicAlgorithm函数。- 在
logarithmicAlgorithm函数中,声明一个整数变量 i 并赋值为 1。- 进入
while循环,检查条件 i < n 是否满足。由于此时 i 的初始值为 1,且 1 小于 16,条件成立,进入循环体。- 在循环体内,使用
printf函数打印变量 i 的值。- 执行
i *= 2,将 i 的值乘以 2。- 回到循环的开头,再次检查条件 i < n。如果条件仍然成立,继续执行循环体;如果条件不成立,跳出循环。
- 当 i 的值达到或超过 n(即 16)时,条件 i < n 不再满足,跳出循环。
- 退出
logarithmicAlgorithm函数。- 回到
main函数,继续执行后续的代码。执行return 0;语句,结束程序。
- 设
while循环的判断执行次数为x, 2 = N , ⇒ 2 x − 1 = l o g 2 N + 1 2 = N,\rArr 2^{x-1} = log_2N+1 2=N,⇒2x−1=log2N+1
while循环内的执行次数为 2 ∗ l o g 2 N 2*log_2N 2∗log2N
- 故而程序的执行次数为: T ( N ) = 7 + 3 ∗ l o g 2 N , T(N)= 7+3 * log_2N, T(N)=7+3∗log2N, lim N → ∞ T ( N ) = O ( l o g N ) \lim\limits_{N\rarr\infin}T(N)=O(logN) N→∞limT(N)=O(logN)。
1.2.4 平方时间复杂度( O ( N 2 ) O(N^2) O(N2)
#include <stdio.h>void quadraticAlgorithm(int n) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {printf("(%d, %d)\n", i, j);}}
}int main() {int n = 3;quadraticAlgorithm(n);return 0;
}这段代码的执行过程如下:
- 在
main函数中声明一个整数变量n,并赋值为3。- 调用
quadraticAlgorithm()函数,并把变量n作为形参传递给函数。- 进入函数
quadraticAlgorithm()。- 外部
for循环的判断执行次数为n+1,外部循环循环一次内部for循环判断的执行次数为n+1,printf语句的执行次数为n。故而外部
for循环的执行次数就为n+1,内部for循环的总执行次数就为n*(n+1),内部for循环的printf语句的总执行次数为 n 2 n^2 n2
- 退出函数
quadraticAlgorithm()。- 继续执行
main函数中的return 0;语句,结束程序。
- 故程序的执行次数为: T ( N ) = 1 + 1 + 1 + ( N + 1 ) + N ∗ ( N + 1 ) + N ∗ N + 1 + 1 = 2 N 2 + 2 N + 6 , T(N) =1+1+1+(N+1)+N*(N+1)+N*N+1+1=2N^2+2N+6, T(N)=1+1+1+(N+1)+N∗(N+1)+N∗N+1+1=2N2+2N+6, lim N → ∞ T ( N ) = O ( N 2 ) \lim\limits_{N\rarr\infin}T(N)=O(N^2) N→∞limT(N)=O(N2)
1.3 常见的函数的时间复杂度
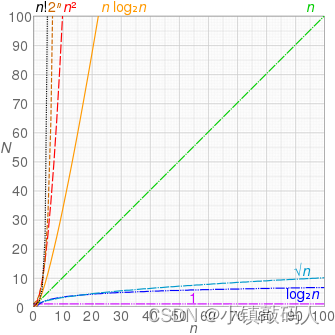
以下图片整理了一些常用的时间复杂度类。表中, p o l y ( x ) = x O ( 1 ) poly(x) = xO(1) poly(x)=xO(1),也就是 x 的多项式。也可以访问网页版点击此处跳转

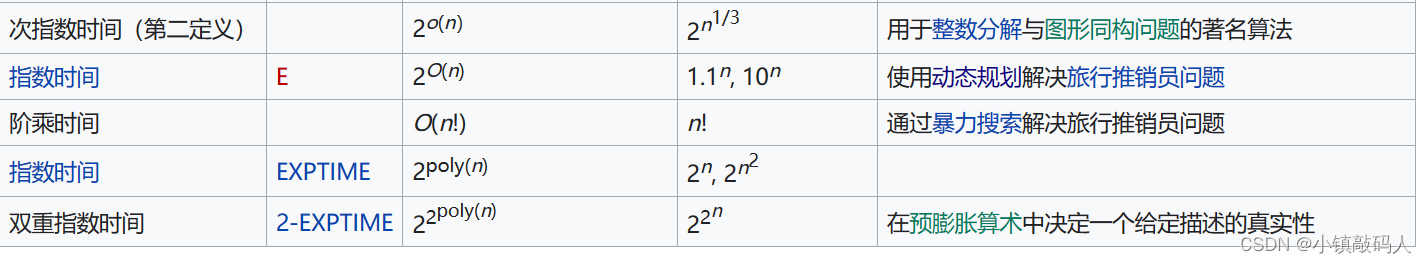
二、空间复杂度
2.1 空间复杂度的定义
在计算机科学中,一个算法或程序的空间复杂度定性地描述该算法或程序运行所需要的存储空间大小。空间复杂度是相应计算问题的输入值的长度的函数,它表示一个算法完全执行所需要的存储空间大小。和时间复杂度类似,空间复杂度通常也使用大O记号来渐进地表示。例如: O ( n ) 、 O ( n α ) 、 O ( n ∗ l o g n ) 、 O ( 2 n ) O(n)、{\displaystyle O(n^{\alpha })}、O(n*logn)、O(2^n) O(n)、O(nα)、O(n∗logn)、O(2n)。
空间复杂度用于评估算法在执行过程中所需的额外空间或内存的量级或增长趋势。它主要关注算法在运行过程中所使用的额外存储空间,包括算法使用的数据结构、临时变量、递归调用等。
- 注意:空间复杂度不计算空间,只计算变量的个数
常见的空间复杂度包括:
- 常数空间复杂度 ( O ( 1 ) ) (O(1)) (O(1)):算法使用固定的额外空间,不随输入的增加而变化。
- 线性空间复杂度 ( O ( n ) ) (O(n)) (O(n)):算法使用的额外空间与输入规模成线性关系。
- 平方空间复杂度 ( O ( n 2 ) ) (O(n^2)) (O(n2)):算法使用的额外空间与输入规模成平方关系。
- 对数空间复杂度 ( O ( l o g n ) ) (O(logn)) (O(logn)):算法使用的额外空间与输入规模成对数关系。
2.2 常见的空间复杂度的计算
- 就是去算变量和函数调用开辟的栈帧的个数之和
2.2.1 常数空间复杂度 ( O ( 1 ) ) (O(1)) (O(1))
void printHello() {printf("Hello, world!\n");
}
- 函数调用一次,开辟一个栈帧,空间复杂度为 O ( 1 ) O(1) O(1)。
2.2.2 线性空间复杂度 ( O ( n ) ) (O(n)) (O(n))
void printNumbers(int n) {int *arr =(int*)malloc(n * sizeof(int));// 执行其他操作...free(arr);
}- 开辟了一个动态数组,变量的个数与 n n n成正比,取极限,和时间复杂度一样,常数可以忽略,空间复杂度为 O ( n ) O(n) O(n)。
2.2.3 平方空间复杂度 ( O ( n 2 ) ) (O(n^2)) (O(n2))
void printPairs(int n) {int **matrix = (int**)malloc(n * sizeof(int *));for (int i = 0; i < n; i++) {matrix[i] = (int*)malloc(n * sizeof(int));}// 执行其他操作...for (int i = 0; i < n; i++) {free(matrix[i]);}free(matrix);
}- 开辟了一个二维的动态数组,变量的个数与 n 2 n^2 n2成正比,取极限,忽略常数,空间复杂度为 O ( n 2 ) O(n^2) O(n2)。
2.2.4 对数空间复杂度 ( O ( l o g n ) ) (O(logn)) (O(logn))
// 递归二分查找函数
int binarySearch(int arr[], int low, int high, int target) {if (low <= high) {int mid = low + (high - low) / 2;if (arr[mid] == target) {return mid;} else if (arr[mid] < target) {return binarySearch(arr, mid + 1, high, target);} else {return binarySearch(arr, low, mid - 1, target);}}return -1; // 如果找不到目标元素,返回-1
}
数组是提前排好序的递增数组,假设同时存在的栈帧最多为x个,因为只有找不到或者找到了
target函数才会返回,此时区间长度要么是1,要么没找到不构成区间了,函数调用产生的栈帧才会开始销毁,有 2 x = n → x = l o g 2 n 2^x=n\to x=log_2n 2x=n→x=log2n,也就是最多开辟了 l o g 2 n log_2n log2n个栈帧。
- 故取极限,空间复杂度 T ( N ) 为 T(N)为 T(N)为 lim N → ∞ T ( N ) = O ( l o g N ) \lim\limits_{N\rarr\infin}T(N)=O(logN) N→∞limT(N)=O(logN)。
相关文章:
【数据结构与算法篇】之时间复杂度与空间复杂度
【数据结构与算法篇】之时间复杂度与空间复杂度 一、时间复杂度1.1时间复杂度的定义1.2 常见的时间复杂度的计算1.2.1 常数时间复杂度( O ( 1 ) ) O(1)) O(1))1.2.2 线性时间复杂度( O ( N ) O(N) O(N))1.2.3 对数时间复杂度( O (…...

硬件性能 - 网络瓶颈分析
简介 本文章主要通过Linux命令查看网络信息、判断是否出现网络瓶颈等简单分析方法。其他硬件性能分析如下: 1. 硬件性能 - CPU瓶颈分析 2. 硬件性能 - 掌握内存知识 3. 硬件性能 - 磁盘瓶颈分析 目录 1. 监控命令 sar 2. 带宽利用率 3. 网络延迟 4. 网络连接数 …...

stm32驱动MCP2515芯片,项目已通过测试
最近公司做一个项目,需要3路can通道,但是stm32看了很久,最多也就只有2个can,所以找到了一款MCP2515芯片,可以用spi驱动can。 已经实现了can的发送和接收,接收采用的是外部中断接收的方式。和单片机本身带的…...
Nginx部署前后端分离项目
dev.env.js解释 //此文件时开发环境配置文件 use strice//使用严格模式 const merge require(webpacl-merge)//合并对象 const prodEnv require(./prod.env)//导出 module.exports merge(prodEnv,{//合并两个配置文件对象并生成一个新的配置文件,如果合并的过程…...

pytorch多分类问题 CrossEntropyLoss()函数的输入size/shape不一致问题
在使用pytorch实现一个多分类任务的时候,许多多分类任务在训练过程中都会有如下的代码: criterion nn.CrossEntropyLoss() loss criterion(output, target) # output.size : [batch_size, class_num] # target.size : [batch_size]许多的初学者会卡在…...

硬盘或者U盘提示需要格式化的解决办法
插入硬盘之后提示: 使用驱动器 G:中的光盘之前需要将其格式化 是否要将其格式化? 如下图所示 顿时慌了啊,里面还有比较重要的东西呢,这一下子完蛋? 遇事找某宝,上面估计有这种技术服务。果然有这一类的技术服务&…...

Clip-Path
前言 借助clip-path,我们可以实现一些复杂的animation动画效果,我们先来简单概述一下它的特性,如MDN所描述的。 The clip-path CSS property creates a clipping region that sets what part of an element should be shown. Parts that are inside the region are shown, whi…...
Matlab绘图系列教程-Matlab 34 种绘图函数示例(下)
Matlab绘图系列教程:揭秘高质量科学图表的绘制与优化 文章目录 Matlab绘图系列教程:揭秘高质量科学图表的绘制与优化第一部分:入门指南1.1 简介关于本教程的目的与范围Matlab绘图在科学研究中的重要性 1.2 准备工作安装Matlab及其工具箱 1.3 …...

【Vue+Django】Training Management Platform Axios并发请求 - 20230703
需求陈述 由于API是特定单位/特定类别/特定教学方式的数据,故汇总数据需要循环请求不同单位/不同类别/不同教学方式。 技术要点 1.axios并发请求 2.JS for循环 3.Vue数组中出现 ob :Observer无法取值问题的解决方法 4.将数据转化为数组 5.一次请求所有数据后&…...
smart Spring:自定义注解、拦截器的使用(更新中...)
文章目录 〇、使用自定义注解的好处和工作原理一、如何使用自定义注解1.自定义一个注解2.在类、属性、方法上进行使用3.元注解 二、使用拦截器的好处和工作原理三、如何使用拦截器参考 本博客源码: 〇、使用自定义注解的好处和工作原理 自定义注解是Java语言提供的…...

php导出pdf
插件官网:TCPDF 博主用的是tp6框架 、tcpdf插件 composer require tecnickcom/tcpdf --ignore-platform-reqs 后面是忽略平台要求的参数 ---------------中文乱码start------------------ 关于中文乱码问题: 网上说的下载字体放入fonts 利用tools…...

【ECMAScript6_2】字符串
1、字符的Unicode表示法 ES6 加强了对 Unicode 的支持,允许采用\uxxxx形式表示一个字符,其中xxxx表示字符的 Unicode 码点。(\u0000-\uFFFF) 码点超过取值范围之后不能正确解读,但是只要给码点加上{}就可以正确解读。 …...
37.RocketMQ之Broker消息存储源码分析
highlight: arduino-light 消息存储文件 rocketMQ的消息持久化在我们在搭建集群时都特意指定的文件存储路径,进入指定的store目录下就可以看到。 下面介绍各文件含义 CommitLog 存储消息的元数据。produce发出的所有消息都会顺序存入到CommitLog文件当中。 CommitLog由多个文件…...
RabbitMq应用延时消息
一.建立绑定关系 package com.lx.mq.bind;import com.lx.constant.MonitorEventConst; import lombok.extern.slf4j.Slf4j; import org.springframework.amqp.core.*; import org.springframework.beans.factory.annotation.Value; import org.springframework.context.annota…...

【WEB自动化测试】- 浏览器操作方法
一、常用方法 1. maximize_window() 最大化窗口 (重点) 说明:如果能够在打开页面时,全屏显示页面,就能尽最大可能加载更多的页面,提高可定位性 2. set_window_size(width, height) 设置浏览器窗口的大小 (了解) 场景࿱…...

VSCode设置鼠标滚轮滑动设置字体大小
1:打开"文件->首选项->设置 2 :打开settings.json文件 英文版这里有个坑 一般点击我下图右上角那个{ } 就可以打开了 在 设置的json 文件中加入如下 “editor.mouseWheelZoom”: true { “editor.mouseWheelZoom”: true, “json.schemas”: [ ]}...
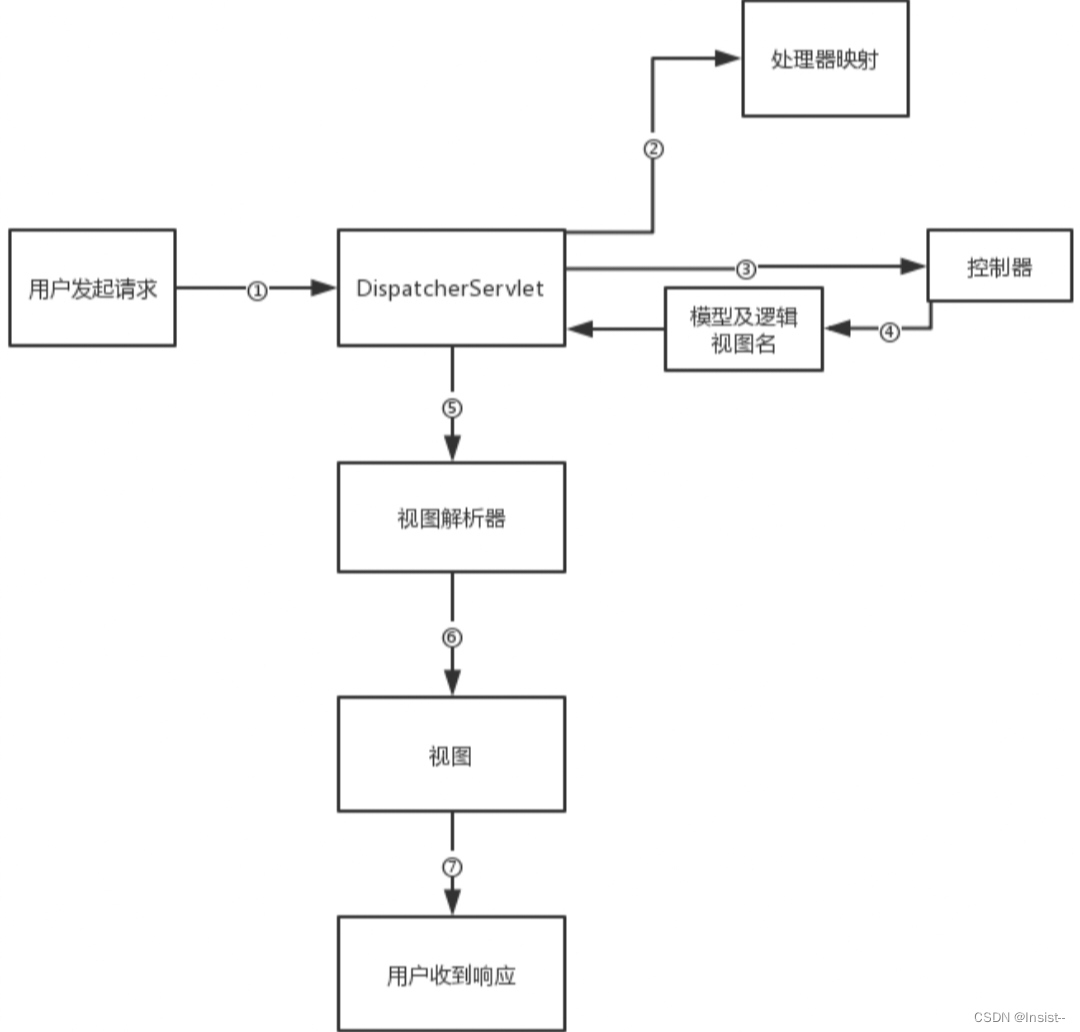
Spring MVC是什么?详解它的组件、请求流程及注解
作者:Insist-- 个人主页:insist--个人主页 作者会持续更新网络知识和python基础知识,期待你的关注 前言 本文将讲解Spring MVC是什么,它的优缺点与九大组件,以及它的请求流程与常用的注解。 目录 一、Spring MVC是什…...
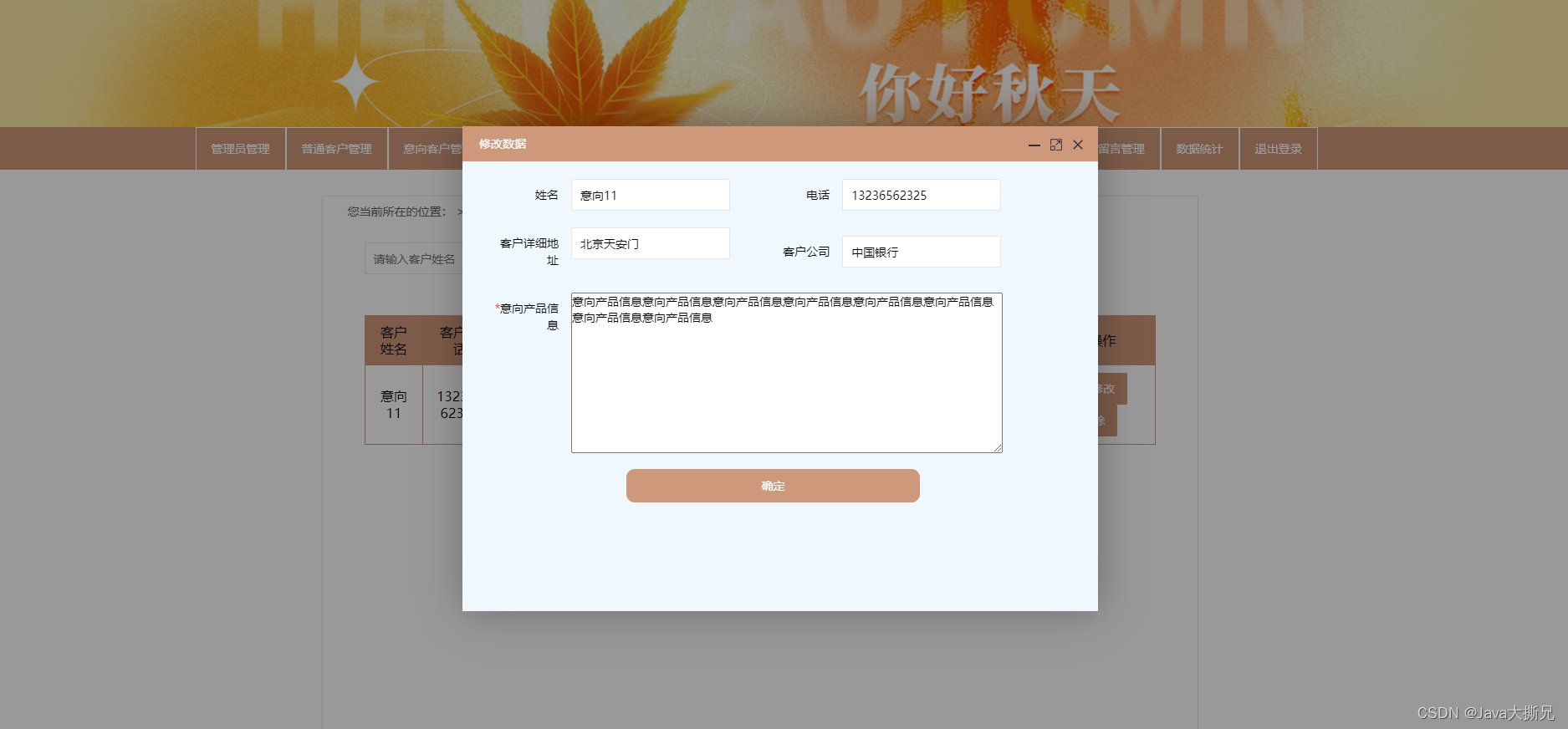
基于Spring Boot的广告公司业务管理平台设计与实现(Java+spring boot+MySQL)
获取源码或者论文请私信博主 演示视频: 基于Spring Boot的广告公司业务管理平台设计与实现(Javaspring bootMySQL) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 后端:Java springboot框架 …...

docker 基本命令安装流程
docker 基本命令安装流程 1.更新Ubuntu的apt源索引 $ sudo apt-get update2.安装包允许apt通过HTTPS使用仓库 $ sudo dpkg --configure -a $ sudo apt-get install apt-transport-https ca-certificates curl software-properties-common3.添加Docker官方GPG key $ curl -f…...
尚硅谷大数据Flink1.17实战教程-笔记02【Flink部署】
尚硅谷大数据技术-教程-学习路线-笔记汇总表【课程资料下载】视频地址:尚硅谷大数据Flink1.17实战教程从入门到精通_哔哩哔哩_bilibili 尚硅谷大数据Flink1.17实战教程-笔记01【Flink概述、Flink快速上手】尚硅谷大数据Flink1.17实战教程-笔记02【Flink部署】尚硅谷…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
