【代码随想录二刷】Day16-二叉树-C++
代码随想录二刷Day16
每日任务
104.二叉树的最大深度
559.n叉树的最大深度
111.二叉树的最小深度
222.完全二叉树的节点个数
语言:C++
104. 二叉树的最大深度
链接:https://leetcode.cn/problems/maximum-depth-of-binary-tree/
递归法(前序遍历)
class Solution {
public:int res = 0;//depth代表当前root所在层的深度void getDepth(TreeNode* root, int depth){res = res > depth ? res : depth;if(root->left == NULL && root->right == NULL) return; //中//左if(root->left){depth++;getDepth(root->left, depth);depth--;}//右if(root->right){depth++;getDepth(root->right, depth);depth--;}}int maxDepth(TreeNode* root) {if(root == NULL) return res;getDepth(root, 1);return res;}
};
递归法(后序遍历)
class Solution {
public:int getDepth(TreeNode* root){if(root == NULL) return 0;int left = getDepth(root->left); //左int right = getDepth(root->right); //右return 1 + max(left, right); //中}int maxDepth(TreeNode* root) {return getDepth(root);}
};
迭代法(层序遍历)
class Solution {
public:int maxDepth(TreeNode* root) {int res = 0;if(root == NULL) return res;queue<TreeNode*> que;que.push(root);while(!que.empty()){int n = que.size();res++;for(int i = 0; i < n; i++){TreeNode* cur = que.front();que.pop();if(cur->left) que.push(cur->left);if(cur->right) que.push(cur->right);}}return res;}
};
559. n叉树的最大深度
链接:https://leetcode.cn/problems/maximum-depth-of-n-ary-tree/
递归法
class Solution {
public:int getDepth(Node* root){if(root == NULL) return 0;int res = 1;for(int i = 0; i < root->children.size(); i++){int depth = getDepth(root->children[i]) + 1;res = res > depth ? res : depth;}return res;}int maxDepth(Node* root) {return getDepth(root);}
};
迭代法(层序遍历)
class Solution {
public:int maxDepth(Node* root) {int res = 0;if(root == NULL) return res;queue<Node*> que;que.push(root);while(!que.empty()){int n = que.size();res++;for(int i = 0; i < n; i++){Node* cur = que.front();que.pop();for(int j = 0; j < cur->children.size(); j++){que.push(cur->children[j]);}}}return res;}
};
111. 二叉树的最小深度
链接:https://leetcode.cn/problems/minimum-depth-of-binary-tree/
递归法(前序遍历)
class Solution {
public:int res = INT_MAX;//depth代表root所在层的深度void getDepth(TreeNode* root, int depth){if(root == NULL) return;if(root->left == NULL && root->right == NULL){res = min(depth, res);return;}//中没有处理逻辑//左if(root->left){depth++;getDepth(root->left, depth);depth--;}//右if(root->right){depth++;getDepth(root->right, depth);depth--;}}int minDepth(TreeNode* root) {if(root == NULL) return 0;getDepth(root, 1);return res;}
};
递归法(后序遍历)
class Solution {
public:int getDepth(TreeNode* root){if(root == NULL) return 0;int left = getDepth(root->left); //左int right = getDepth(root->right); //右if(root->left == NULL && root->right != NULL) return right + 1;if(root->left != NULL && root->right == NULL) return left + 1;return 1 + min(left, right); //中}int minDepth(TreeNode* root) {return getDepth(root);}
};
迭代法(层序遍历)
class Solution {
public:int minDepth(TreeNode* root) {int res = 0;if(root == NULL) return res;queue<TreeNode*> que;que.push(root);while(!que.empty()){int n = que.size();res++;for(int i = 0; i < n; i++){TreeNode* cur = que.front();que.pop();if(!cur->left && !cur->right) return res;if(cur->left) que.push(cur->left);if(cur->right) que.push(cur->right);}}return res;}
};
222. 完全二叉树的节点个数
链接:https://leetcode.cn/problems/count-complete-tree-nodes/
普通二叉树(递归-后序遍历)
class Solution {
public:int getNumber(TreeNode* root){if(root == NULL) return 0;if(root->left == NULL && root->right == NULL) return 1;int left = getNumber(root->left);int right = getNumber(root->right);return left + right + 1;}int countNodes(TreeNode* root) {if(root == NULL) return 0;return getNumber(root);}
};
普通二叉树(迭代-层序遍历)
class Solution {
public:int countNodes(TreeNode* root) {if(root == NULL) return 0;queue<TreeNode*> que;que.push(root);int res = 0;while(!que.empty()){int n = que.size();res += n;for(int i = 0; i < n; i++){TreeNode* cur = que.front();que.pop();if(cur->left) que.push(cur->left);if(cur->right) que.push(cur->right);}}return res;}
};
完全二叉树
① 满二叉树:2^树深度-1
② 最后一层叶子节点没满:分别递归左孩子和右孩子,一定会有某个左孩子或右孩子为满二叉树
class Solution {
public:int countNodes(TreeNode* root) {if(root == NULL) return 0;int left = 0;int right = 0;TreeNode* cur = root;while(cur->left){cur = cur->left;left++;}cur = root;while(cur->right){cur = cur->right;right++;}if(left == right){return (2 << left) - 1;}return countNodes(root->left) + countNodes(root->right) + 1;}
};
相关文章:

【代码随想录二刷】Day16-二叉树-C++
代码随想录二刷Day16 每日任务 104.二叉树的最大深度 559.n叉树的最大深度 111.二叉树的最小深度 222.完全二叉树的节点个数 语言:C 104. 二叉树的最大深度 链接:https://leetcode.cn/problems/maximum-depth-of-binary-tree/ 递归法(前序…...

Lecture5 实现线性回归(Linear Regression with PyTorch)
目录 1 Pytorch实现线性回归 1.1 实现思路 1.2 完整代码 2 各部分代码逐行详解 2.1 准备数据集 2.2 设计模型 2.2.1 代码 2.2.2 代码逐行详解 2.2.3 疑难点解答 2.3 构建损失函数和优化器 2.4 训练周期 2.5 测试结果 3 线性回归中常用优化器 1 Pytorch实现线性回归…...

Python与Matlab svd分解的差异
1.差异说明 Matlab和Python的NumPy库中的SVD函数(np.linalg.svd)都是用来对矩阵进行奇异值分解(SVD)的函数,但它们在默认参数和返回结果方面有一些差异。 在Matlab中,SVD函数的默认行为是计算矩阵的完整SVD,即对于一…...

2023年光模块行业发展趋势及未来前景
随着数字化时代的到来,互联网行业的快速发展,网络通信设备行业的发展也在逐渐加速。光模块作为网络设备的重要组成部分,也在不断创新和发展。那么,光模块行业的未来发展趋势又是怎样的呢?接下来就跟着易天光通信&#…...

Sysmac Studio使用Tortoise和Git实现版本控制
Sysmac Studio使用Tortoise和Git实现版本控制实验时间:2022/11/16 实验软件:Sysmac Studio(1.52,需要软件授权支持版本控制)、Git(2.38.1)、Tortoise(2.13.0)、gitee(代码仓库) 实验目的:Sysmac Studio实现版本控制、多人同时开…...

Intent 和 Bundle 传值的区别
文章目录1、使用上1.1 Intent 方式1.2 Bundle 方式2、为什么 Bundle 使用 ArrayMap 而不是 Hashmap 实现呢?1、使用上 1.1 Intent 方式 举例:将数据从页面 A 传递到 B,然后再传递到 CA 页面: Intent intentnew Intent(MainActi…...

TypeScript 初步
一、TypeScript是什么? Typed JavaScript at Any Scale: 添加了类型系统的JavaScript,使用于任何规模的项目。 两个重要特点: 类型系统 任何规模 中文官网:文档简介 TypeScript中文网 TypeScript——JavaScript的超集 TypeS…...
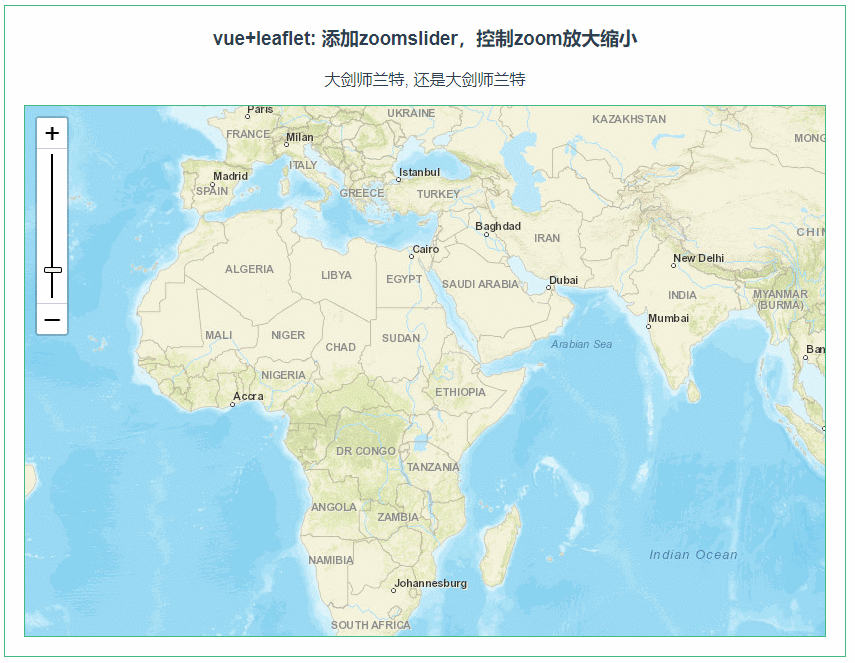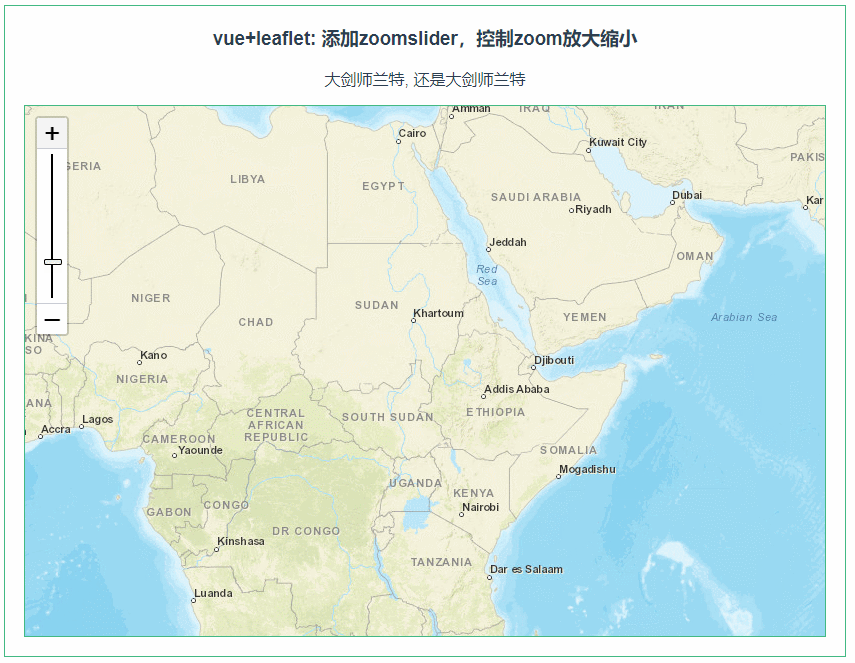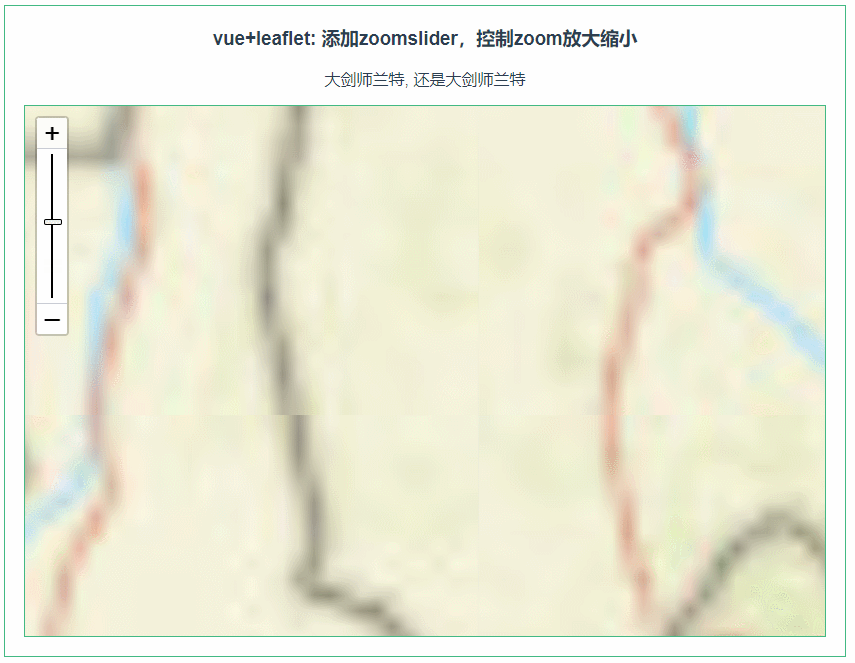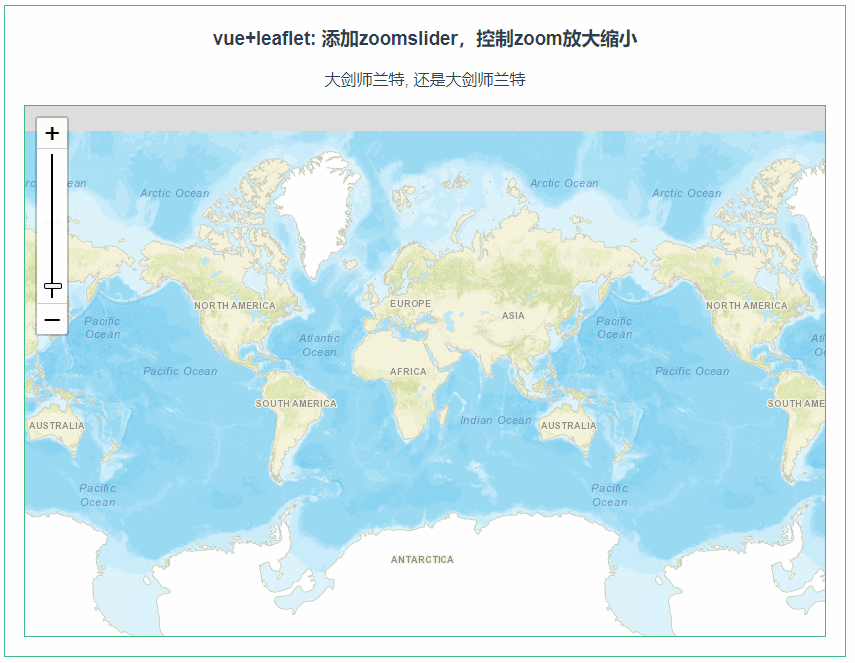
leaflet 添加zoomslider,控制zoom放大缩小(074)
第074个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet中使用zoomslider,相比于普通的zoom控件,这个更加形象,更加具体些。 直接复制下面的 vue+leaflet源代码,操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码(共65行)相关API参考:专栏目…...

10分钟学会python对接【OpenAI API篇】
今天学习 OpenAI API,你将能够访问 OpenAI 的强大模型,例如用于自然语言的 GPT-3、用于将自然语言翻译为代码的 Codex 以及用于创建和编辑原始图像的 DALL-E。 首先获取生成 API 密钥 在我们开始使用 OpenAI API 之前,我们需要登录我们的 Op…...

2023美赛必须注意事项
文章目录首页部分要求竞赛期间题目查看题目下载论文要求比赛提示控制号提交解决方案更多注意事项首页部分要求 具体如下: 我提取一些关键词如下: 第一页:摘要页字体要求:12点的 Times New Roman 字体请勿在此页面或任何页面上…...
基于微信小程序的智能招聘小程序
文末联系获取源码 开发语言:Java 框架:ssm JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7/8.0 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 浏览器…...

Java文件操作和I/O
Java 流(Stream)、文件(File)和IOJava.io 包几乎包含了所有操作输入、输出需要的类。所有这些流类代表了输入源和输出目标。Java.io 包中的流支持很多种格式,比如:基本类型、对象、本地化字符集等等。一个流可以理解为一个数据的序列。输入流表示从一个源…...
QT项目_RPC(进程间通讯)
QT项目_RPC(进程间通讯) 前言: 两个进程间通信、或是说两个应用程序之间通讯。实际情况是在QT开发的一个项目中,里面包含两个子程序,子程序有单独的界面和应用逻辑,这两个子程序跑起来之后需要一些数据的交互,例如&…...

移动硬盘文件丢失怎么恢复?
在我们的日常工作、学习和生活都离不开各种数据。每天都会接收或处理各种数据,尤其是做设计、自媒体、多媒体设计的人。移动硬盘成为我们常备的存储工具,但有使用就会伴随着意外情况的发生,这将导致移动硬盘上数据的丢失,比如误删…...
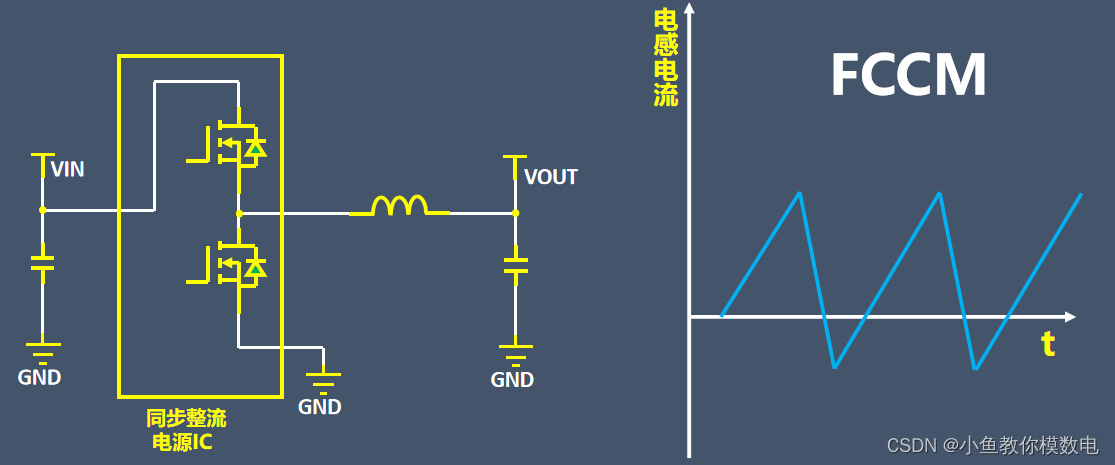
什么是同步整流和异步整流
在设计降压型DCDC电路的时候,经常会听到同步整流(synchronous)和异步整流(asynchronous)。那么什么是同步整流,什么是异步整流呢从这两种电路的拓扑来看,异步整流型外围有一个续流二极管&#x…...

关于PYTHON Enclosing 的一个小问题
问题分析 以下是一段每隔半小时重复执行测试用例的脚本,func是传入的测试函数,在执行func前后,会打印操作次数 def repeat(func, action):try:log.info(u******开始并发%s****** % action)thread_list []for i in range(repeat_count):def…...

LabVIEW错误-2147220623:最大内存块属性不存在
LabVIEW错误-2147220623:最大内存块属性不存在在使用NI Linux实时操作系统目标中,使用系统属性节点和分布式系统管理器(DSM),但遇到一些问题:它未正确报告系统上的可用物理内存量。在NI Linux实时系统上出现…...

图的总复习
一、图的定义Graph 图是由顶点vertex集合及顶点间关系集合组成的一种数据结构: 顶点的集合 和 边的集合 二、无向图 用(x,y)表示两个顶点x和y之间的一条边(edge) 边是无方向的 N{V,E},V{0…...

测试流程记录
1,需求评审 2,技术方案评审 3,编写测试用例 编写需求分析 编写测试用例 编写冒烟case 4,用例评审 5,提测 提测前给开发执行冒烟case 6,测试 测试完成前约产品验收时间 7,验收 跟进验收问题…...

Mysql主从架构与实例
mysql的主从架构 MySQL主从架构是一种常见的数据库高可用性解决方案,它通常由一个主数据库和多个从数据库组成。主数据库用于处理写入请求和读取请求,从数据库则用于处理只读请求。 在主从架构中,主数据库记录所有数据更改并将这些更改同步…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
