【代码随想录训练营】【Day16】第六章|二叉树|104.二叉树的最大深度|559.n叉树的最大深度|111.二叉树的最小深度|222.完全二叉树的节点个数
二叉树的最大深度
题目详细:LeetCode.104
递归法很容易理解:
- 定义一个全局变量max, 记录二叉树的最大深度
- 在递归函数中增加一个深度参数,表示当前的节点的深度
- 然后对二叉树进行深度优先遍历
- 当遍历到叶子节点时,比较当前节点的深度和记录的最大深度,保持最大值
- 当树遍历完成后,返回记录的最大深度即可
Java解法(递归,深度优先遍历):
class Solution {private int max = 0;public int maxDepth(TreeNode root) {this.dfs(root, 0);return this.max;}public void dfs(TreeNode root, int deep){if(null == root){this.max = deep > this.max ? deep : this.max;return;}this.dfs(root.left, deep + 1);this.dfs(root.right, deep + 1);}
}
递归法很容易掌握,所以我想尝试用迭代法来解题,但使用前序遍历迭代法来解题好像不是很方便;回到观察问题本身,我发现求二叉树的最大深度,其实就是求叶子节点的最大层数,那么我们也可以利用层序遍历(广度优先遍历)来解题:
Java解法(层序遍历,迭代法,广度优先遍历):
class Solution {public int maxDepth(TreeNode root) {return this.bfs(root);}public int bfs(TreeNode root){Queue<TreeNode> queue = new LinkedList<>();if(null != root) queue.offer(root);int deep = 0;while(!queue.isEmpty()){deep++;int len = queue.size();while(len-- > 0){TreeNode node = queue.poll();if(null != node.left) queue.offer(node.left);if(null != node.right) queue.offer(node.right);}}return deep;}
}
n叉树的最大深度
题目详细:LeetCode.559
这道题和上一题的二叉树的最大深度有异曲同工之妙,区别在于:
- n叉树的多个节点,使用的是指针数组来存储
- 除了根节点可能为空外,在遍历孩子节点过程中,不会遍历到空节点
- 叶子节点的定义有两种情况:
- 孩子节点数组为空(即 node.children == null ,这种情况在样本数据中未出现)
- 孩子节点数组长度为 0
所以这道题利用递归法来解决非常简单,跟求解二叉树的最大深度的过程类似,只是这次改为对每一个孩子节点都进行深度优先遍历,最后保留深度最大值。
Java解法(递归,深度优先遍历):
class Solution {public int maxDepth(Node root) {return this.dfs(root);}public int dfs(Node root){int deep = 0;if(null == root) return deep;for(Node node: root.children){deep = Math.max(deep, this.dfs(node));}return deep + 1;}
}
二叉树的最小深度
题目详细:LeetCode.111
这道题与上面找二叉树的最大深度刚好相反,要求找二叉树的最小深度,但是其解题思路是相似的:
- 同样是遍历到树的叶子节点,只不过一个是记录树的最大深度,一个是记录树的最小深度罢了
- 这道题的难点在于如何确定是否到达了叶子节点
- 因为求二叉树的最大深度时,我们并不需要去关心当前节点是否是叶子节点
- 我们只需要注意当遍历到空节点时进行回溯,即空节点的深度 - 1,同时与记录的深度进行比较,保持一个最大值即可
- 但是在求二叉树的最小深度时,就不一样了,因为在遍历到空节点时,会出现这四种情况,都有着各自的处理方式:
- 当前节点的左节点为空,但其右节点不为空,非叶子节点,继续遍历右子树查找叶子节点
- 当前节点的左节点不为空,但其右节点为空,非叶子节点,继续遍历右子树查找叶子节点
- 当前节点的左右节点都不为空 ,继续遍历左右子树查找叶子节点
- 当前节点的左右节点都为空,属于叶子节点,比较当前节点的深度并记录最小深度
- 因为求二叉树的最大深度时,我们并不需要去关心当前节点是否是叶子节点
- 可见,在求二叉树的最小深度的过程中,并不涉及回溯,因为如果遍历到空节点就回溯的话,其回溯到的节点不一定是叶子节点
- 在求解过程中,只有必须判断当前节点是否是叶子节点,才能够更新记录值。
Java解法(递归,深度优先遍历,模拟思路版):
class Solution {private int min = Integer.MAX_VALUE;public int minDepth(TreeNode root) {if(null != root){this.dfs(root, 1);return min;}return 0;}public void dfs(TreeNode root, int deep){if(null != root && null == root.left && null == root.right){min = Math.min(min, deep);return;}if(null != root.left) this.dfs(root.left, deep + 1);if(null != root.right) this.dfs(root.right, deep + 1);}
}
Java解法(递归,深度优先遍历,精简版):
class Solution {public int minDepth(TreeNode root) {return dfs(root);}public int dfs(TreeNode root){if(null == root) return 0;if(null != root.left && null == root.right)return 1 + dfs(root.left);if(null == root.left && null != root.right)return 1 + dfs(root.right);return 1 + Math.min(dfs(root.left), dfs(root.right));}
}
虽然递归法写起来很简单方便,但是经过测试发现,利用递归来解这道题,虽然能够AC,但是速度并不快,为什么呢?
- 因为递归法的算法思想,是深度优先遍历
- 在二叉树中,它需要去对左右子树都进行深度优先遍历,得到各自的最小深度,然后再比较两者选取一个最小值
- 假如二叉树的左子树深度很小,但是右子树的深度很大
- 那么我们本来只需要通过左子树就可以确定最小深度,却还需要去等待右子树的递归结果,才可以得到最终的结果
- 那毫无疑问,递归右子树是在做无用功的
那么也就是说,我们可以按从上到下,从左到右的顺序来遍历树,假设我们优先在左子树就遍历到了叶子节点得到其深度,那么后面的节点我们都可以不用去关心了,其叶子节点的深度就是二叉树的最小深度,所以优化这道题的关键就在于遍历方式,所以我们可以利用层序遍历来优化这道题:
Java解法(迭代法,层序遍历,广度优先遍历):
class Solution {public int minDepth(TreeNode root) {if(root == null) return 0;return bfs(root);}public int bfs(TreeNode root){Queue<TreeNode> queue = new LinkedList<>();if(null != root) queue.offer(root);int deep = 1;while(!queue.isEmpty()){int n = queue.size();while(n-- > 0){root = queue.poll();if(null == root.left && null == root.right) return deep;if(null != root.left) queue.offer(root.left);if(null != root.right) queue.offer(root.right);}deep++;}return deep;}
}
完全二叉树的节点个数
题目详细:LeetCode.222
这道题如果不涉及完全二叉树,那么我们用任何一种遍历方式来统计二叉树中的节点个数都是可以的,只需要一遍遍历,一边个数 + 1就行了,那么我们可以得到非常大智若愚的递归解法:
Java解法(递归,深度优先遍历,前序遍历):
class Solution {public int countNodes(TreeNode root) {if(null == root) return 0;return 1 + countNodes(root.left) + countNodes(root.right);}
}
那么这道题又何必是求完全二叉树的节点个数呢,为什么不直接让我求二叉树的节点个数就得了?此时,我注意到题目最下面一段小字:
进阶:遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗?
确实,我们如果使用遍历树的方法来统计节点,得到的都是时间复杂度为 O(n) 的算法,完全没有利用到样本数据是一棵完全二叉树的特点,关于完全二叉树的概念和特点详细可以查阅:《代码随想录》— 完全二叉树
在了解了完全二叉树的特点之后,我们不难发现,我们可以利用层序遍历:
- 当遍历到当前节点的某一子节点为空时,那么我们就可以确定其空子节点之前的节点都是非空的
- 那么只需要
累计之前遍历过的节点数量 + 与空子节点同一层的之前的节点长度,就可以得到该完全二叉树的节点个数了
Java解法(迭代法,广度优先遍历,层序遍历):
class Solution {public int countNodes(TreeNode root) {return this.bfs(root);}public int bfs(TreeNode root){Queue<TreeNode> queue = new LinkedList<>();if(null != root) queue.offer(root);int sum = 0;while(!queue.isEmpty()){int n = queue.size();while(n-- > 0){sum++;root = queue.poll();if(null != root.left) queue.offer(root.left);if(null != root.right) queue.offer(root.right);if(null == root.left || null == root.right){return sum + queue.size();}}}return sum;}
}
前两天对二叉树的题我都做得很详细,所以基础算是牢固,而且通过昨天的联系,也明白了二叉树的题目无非就是两个要点:选择最合适的遍历方法 + 处理节点的逻辑方法,在今天的练习过后,我更加肯定了这一观点,并且对二叉树不同的遍历方法更加重视了。
题目看似不停的变,其实万变不离其宗,只要遍历方法选对了,剩下的只需要根据题目需求来处理目标节点就可以解题了,对二叉树的遍历越理解,以及不同类型二叉树各自的特点越熟悉,解起二叉树的题来简直就是得心应手,令我感叹道:
读书破万卷,下笔如有神。
相关文章:

【代码随想录训练营】【Day16】第六章|二叉树|104.二叉树的最大深度|559.n叉树的最大深度|111.二叉树的最小深度|222.完全二叉树的节点个数
二叉树的最大深度 题目详细:LeetCode.104 递归法很容易理解: 定义一个全局变量max, 记录二叉树的最大深度在递归函数中增加一个深度参数,表示当前的节点的深度然后对二叉树进行深度优先遍历当遍历到叶子节点时,比较…...
transformer总结
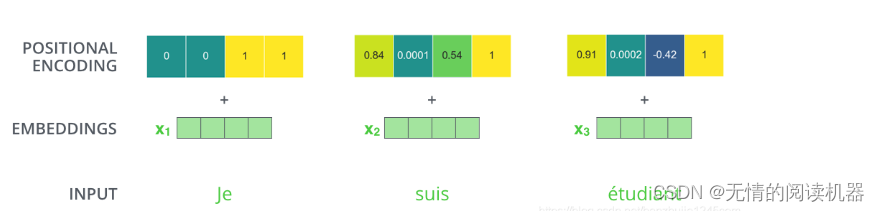
1.注意力机制 意义:人类的注意力机制极大提高了信息处理的效率和准确性。 公式: 1)自注意力机制 b都是在考虑了所有a的情况下生成的。 以产生b1向量为例: 1.在a这个序列中,找到与a1相关的其他向量 2.每个向量与a1关联的程度&a…...

dart flutter入门教程,开发手册 分享
我最近在学校dart flutter.这是我收集的一些手册和教程. 不需要关注公众号,不需要加好友. 我发现flutter(dart)的中文资料比较奇缺.入门的教程非常多.但是api手册几乎没有(全是英文的). 收集原则 1.中文(我英文不好) 2.不要pdf的,网上有一些pdf的 从入门到进阶的,但是太长…...

教育舆情监测关键词有哪些,TOOM教育舆情监测系统流程?
教育舆情监测是指对教育领域的舆情进行收集、分析和处理的过程。舆情是指公众在各种渠道上对教育政策、教育机构、教育事件等方面的言论、态度和情绪。通过对教育舆情的监测和分析,可以了解公众对教育行业的看法和反应,提高对教育行业的管控能力…...
MySQL高级(一)
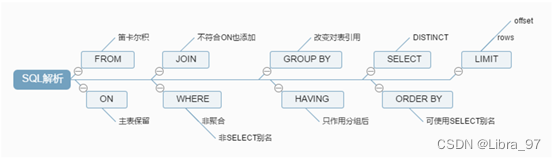
MySQL-day01 1 MySQL简介 1.1 MySQL简介 MySQL是一个关系型数据库管理系统,由瑞典MySQL AB(创始人Michael Widenius)公司开发,2008被Sun收购(10亿美金),2009年Sun被Oracle收购。MariaDBMaria…...
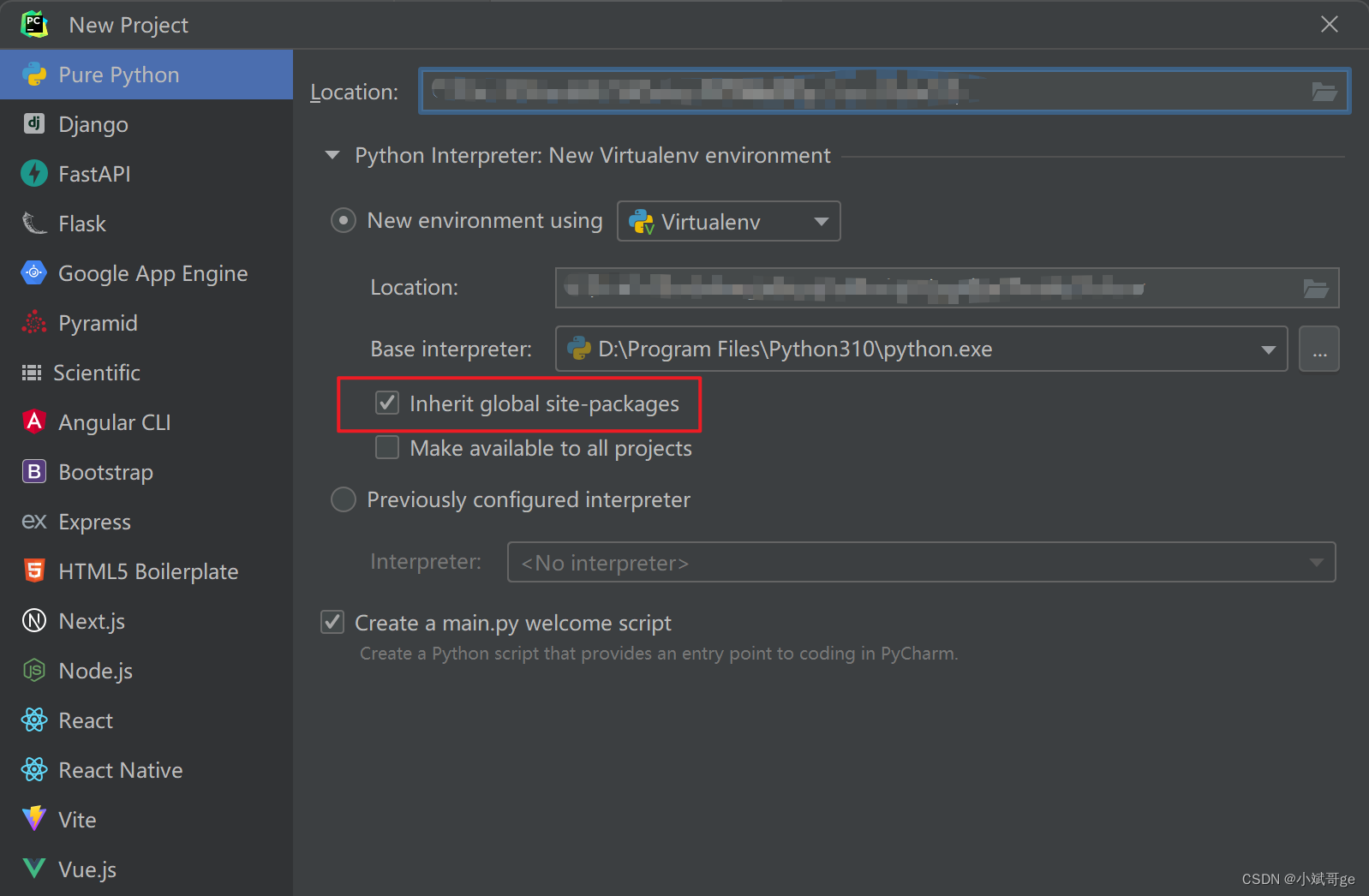
如何将Python项目部署到新电脑上运行?
如何将Python项目部署到新电脑上运行? 在工作中,可能需要在新服务器上部署项目代码,例如新增服务器、把测试环境的代码部署到生产环境等。 在生活中,也会遇到换新电脑,需要将自己在旧电脑上写的(项目&…...
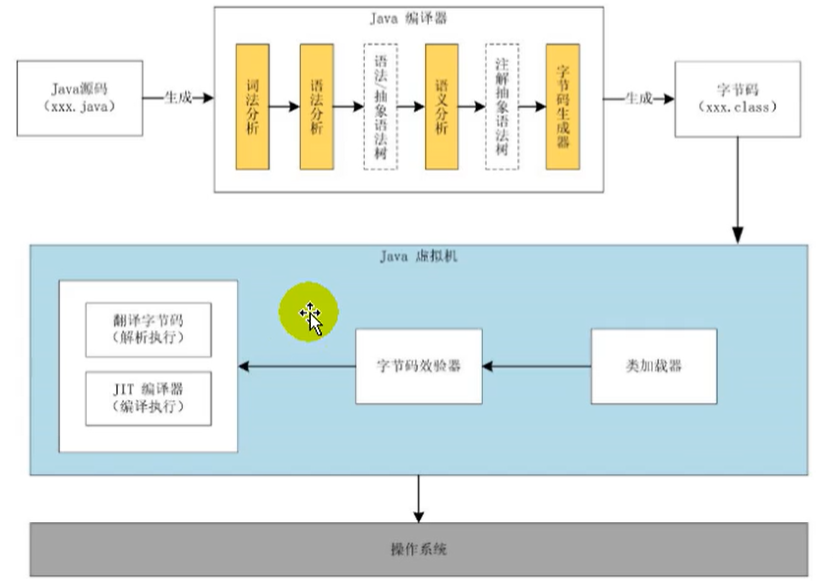
JVM和JAVA体系结构
1、为什么要学习JVM作为Java工程师的你曾被伤害过吗?你是否也遇到过这些问题?运行着的线上系统突然卡死,系统无法访问,甚至直接OOM想解决线上JVM GC问题,但却无从下手新项目上线,对各种JVM参数设置一脸茫然…...
(十)、通过云对象修改阅读量+点赞功能的实现【uniapp+uinicloud多用户社区博客实战项目(完整开发文档-从零到完整项目)】
1,通过云对象importObj修改阅读量 1.1 新建云对象 1.2 云对象中写自增自减方法 封装云对象utilsObj中的自增自减方法,方法名取为operation,传递4个参数。 // 云对象教程: https://uniapp.dcloud.net.cn/uniCloud/cloud-obj // jsdoc语法提…...
)
刷力扣的第一天脑子要长出来的感觉(怎么有人大四才开始啊啊啊啊啊啊啊啊啊啊啊啊,又是等成绩的一天,)
刷力扣的第一天脑子要长出来的感觉(为什么大四才开始啊啊啊啊啊啊啊啊啊啊啊啊) emmm,自己还是想不太出来(只是一点想法),可能还是会参考评论区,求各位轻喷 分析:带符号一定不是回…...
Nuclei文*件上*传FUZZ POC
目录 1.前言 2. Nuclei文件上传FUZZ POC 3. 实战中的应用 1.前言 该文件上传FUZZ POC主要来源于一个靶*场,该POC 主要用来FUZZ目标js页面中的upload ajax请求,以此来进一步尝试文件上传漏*洞利*用。 这里也要感谢下“打工仔1号”提供的开*发人员常见的文*件上*传javaScr…...

完美解决方案-雪花算法ID到前端之后精度丢失问题
最近公司的一个项目组要把以前的单体应用进行为服务拆分,表的ID主键使用Mybatis plus默认 的雪花算法来生成。 快下班的时候,小伙伴跑过来找我,:“快给我看看这问题,卡这卡了小半天了!”。连拉带拽&#x…...

工程管理系统源码之高效的工程项目管理软件
高效的工程项目管理软件不仅能够提高效率还应可以帮你节省成本提升利润 在工程行业中,管理不畅以及不良的项目执行,往往会导致项目延期、成本上升、回款拖后,最终导致项目整体盈利下降。企企管理云业财一体化的项目管理系统,确保…...

390. 消除游戏
列表 arr 由在范围 [1, n] 中的所有整数组成,并按严格递增排序。请你对 arr 应用下述算法:从左到右,删除第一个数字,然后每隔一个数字删除一个,直到到达列表末尾。重复上面的步骤,但这次是从右到左。也就是…...

springBoot JPA代码生成器
介绍通过IDEA配置文件,根据数据库表结构快速生产Service、ServiceImpl、repository、repositoryImpl、自动生成常用的jpa增删改查等方法。使用的版本Spring Boot2.1.6.RELEASE spring-boot-starter-data-jpa使用idea 生成代码步骤打开idea(https://images.gitee.co…...

相同月利率条件下不同还款方式贷款的APR与IRR研究
文章目录前提假设一次性还本付息先息后本等额本息等额本金简单二分法求解IRR的程序汇总实验对比前提假设 因为常见的信贷产品还款期数定义都是按照月,假设只借一期的利率(月利率)为r,在此条件下,研究不同还款方式下的…...

【论文】智能隧道检测车的现状及改进策略
本文转载自《智慧城轨》2022年第11期 作者:黄丹樱1,韦强1,朱椰毅2,范骁1,林浩立1 单位:1 浙江师范大学工学院;2 浙江金温铁道开发有限公司 声明:本文仅用于学术分享,不做商业用途,如有侵权,联…...

【代码随想录二刷】Day16-二叉树-C++
代码随想录二刷Day16 每日任务 104.二叉树的最大深度 559.n叉树的最大深度 111.二叉树的最小深度 222.完全二叉树的节点个数 语言:C 104. 二叉树的最大深度 链接:https://leetcode.cn/problems/maximum-depth-of-binary-tree/ 递归法(前序…...

Lecture5 实现线性回归(Linear Regression with PyTorch)
目录 1 Pytorch实现线性回归 1.1 实现思路 1.2 完整代码 2 各部分代码逐行详解 2.1 准备数据集 2.2 设计模型 2.2.1 代码 2.2.2 代码逐行详解 2.2.3 疑难点解答 2.3 构建损失函数和优化器 2.4 训练周期 2.5 测试结果 3 线性回归中常用优化器 1 Pytorch实现线性回归…...

Python与Matlab svd分解的差异
1.差异说明 Matlab和Python的NumPy库中的SVD函数(np.linalg.svd)都是用来对矩阵进行奇异值分解(SVD)的函数,但它们在默认参数和返回结果方面有一些差异。 在Matlab中,SVD函数的默认行为是计算矩阵的完整SVD,即对于一…...

2023年光模块行业发展趋势及未来前景
随着数字化时代的到来,互联网行业的快速发展,网络通信设备行业的发展也在逐渐加速。光模块作为网络设备的重要组成部分,也在不断创新和发展。那么,光模块行业的未来发展趋势又是怎样的呢?接下来就跟着易天光通信&#…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
