CF1790E Vlad and a Pair of Numbers 题解
CF1790E Vlad and a Pair of Numbers 题解
- 题目
- 链接
- 字面描述
- 题面翻译
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 思路
- 代码实现
题目
链接
https://www.luogu.com.cn/problem/CF1790E
字面描述
题面翻译
共有 ttt 组数据。
每组数据你会得到一个正整数 xxx,你需要构造一组正整数 aaa 和 bbb,满足:
-
a+b=x×2a + b = x \times 2a+b=x×2;
-
axorb=xa \operatorname{xor} b = xaxorb=x,其中 xor\operatorname{xor}xor 指异或。
输出你构造的 aaa 和 bbb。如有多解,任意输出一解即可。如无解,输出 −1-1−1。
1≤t≤1041 \leq t \leq 10^41≤t≤104,1≤x≤2291 \leq x \leq 2^{29}1≤x≤229。同时,你需要保证你构造的 aaa,bbb 满足 1≤a,b≤2301 \leq a,b \leq 2^{30}1≤a,b≤230。
题目描述
Vlad found two positive numbers $ a $ and $ b $ ( $ a,b>0 $ ). He discovered that $ a \oplus b = \frac{a + b}{2} $ , where $ \oplus $ means the bitwise exclusive OR , and division is performed without rounding…
Since it is easier to remember one number than two, Vlad remembered only $ a\oplus b $ , let’s denote this number as $ x $ . Help him find any suitable $ a $ and $ b $ or tell him that they do not exist.
输入格式
The first line of the input data contains the single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases in the test.
Each test case is described by a single integer $ x $ ( $ 1 \le x \le 2^{29} $ ) — the number that Vlad remembered.
输出格式
Output $ t $ lines, each of which is the answer to the corresponding test case. As the answer, output $ a $ and $ b $ ( $ 0 < a,b \le 2^{32} $ ), such that $ x = a \oplus b = \frac{a + b}{2} $ . If there are several answers, output any of them. If there are no matching pairs, output -1.
样例 #1
样例输入 #1
6
2
5
10
6
18
36
样例输出 #1
3 1
-1
13 7
-1
25 11
50 22
思路
根据题目 a+b=2x和aa+b=2x和aa+b=2x和a xorxorxor b=xb=xb=x
我们能发现一个非常高重要的突破点a异或b流失了xa异或b流失了xa异或b流失了x
∴a按位与b=x/2a按位与b=x/2a按位与b=x/2
∵题目可输出任意解
∴a=x/2,b=x+x/2a=x/2,b=x+x/2a=x/2,b=x+x/2
但我们还要考虑一个无解的情况:
当x是奇数时,无法被2整除,无解
当(x/2)按位与x!=0(x/2)按位与x!=0(x/2)按位与x!=0,有误,无解
OK,过程理完,上代码
代码实现
#include<bits/stdc++.h>
using namespace std;int t,n;
int main(){scanf("%d",&t);while(t--){scanf("%d",&n);if(n%2==1){printf("-1\n");continue;}if(((n/2)&n)!=0){printf("-1\n");continue;}printf("%d %d\n",n/2,n/2+n);}return 0;
}
相关文章:

CF1790E Vlad and a Pair of Numbers 题解
CF1790E Vlad and a Pair of Numbers 题解题目链接字面描述题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1思路代码实现题目 链接 https://www.luogu.com.cn/problem/CF1790E 字面描述 题面翻译 共有 ttt 组数据。 每组数据你会得到一个正整数 xxx&…...

漏洞预警|Apache Kafka Connect JNDI注入漏洞
棱镜七彩安全预警 近日网上有关于开源项目Apache Kafka Connect JNDI注入漏洞,棱镜七彩威胁情报团队第一时间探测到,经分析研判,向全社会发起开源漏洞预警公告,提醒相关安全团队及时响应。 项目介绍 Karaf是Apache旗下的一个开…...

企业小程序开发步骤【教你创建小程序】
随着移动互联网的兴起,微信已经成为了很多企业和商家必备的平台,而其中,微信小程序是一个非常重要的工具。本文将为大家介绍小程序开发步骤,教你创建小程序。 步骤一、注册小程序账号 先准备一个小程序账号,在微信公…...

刚性电路板的特点及与柔性电路板的区别
打开市场上的任何一个电子产品,会发现里面都有一块或多块电路板。电路板是电子产品运行的核心,之前沐渥小编已经给大家介绍了柔性电路板,下面给大家介绍刚性电路板的基础知识。 刚性电路板俗称硬板,是由不容易变形的刚性基材制成的…...

扫码过磅+车牌识别,内蒙古蒙维过磅实现信息化管理
扫码过磅、车牌识别、对接SAP ERP系统设计思路: 无人值守系统升级改造包括车牌自动识别系统、信息化(扫码等方式)管理系统、智能自动控制系统等实现信息无纸化传递。远程监管地点设于公司东磅房,可以实现远程监测监控画面、称重过…...
蒙特卡洛计算圆周率
使用MC计算圆周率的小例子,使用python的numpy,matplotlib库import numpy as npimport matplotlib.pyplot as pltdef mc_calculate_pi(t):np.random.seed(t)rand_num np.random.rand(t)rand_num2 np.random.rand(t)l1 rand_num-0.5l2 rand_num2-0.5l0…...
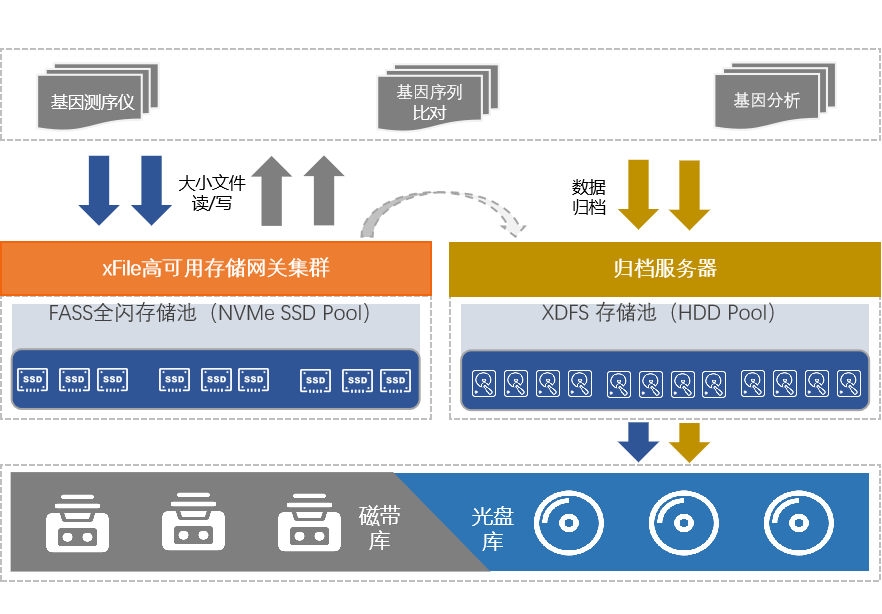
生物信息场景下的用户需求
背景分析概念定义基因测序是一种新型基因检测技术,是基因检测的方法之一,其又叫基因谱测序,是国际上公认的一种基因检测标准。基因测序技术能锁定病变基因,提前预防和治疗。过长的测序周期以及上万美元的仪器成本,成了…...
和sudo(superuser do)的区别?(sudo su与su的区别))
linux su(switch user)和sudo(superuser do)的区别?(sudo su与su的区别)
文章目录linux su(switch user)和sudo(superuser do)的区别?sudo su与su的区别linux su(switch user)和sudo(superuser do)的区别? 在Unix或Linux操作系统中…...
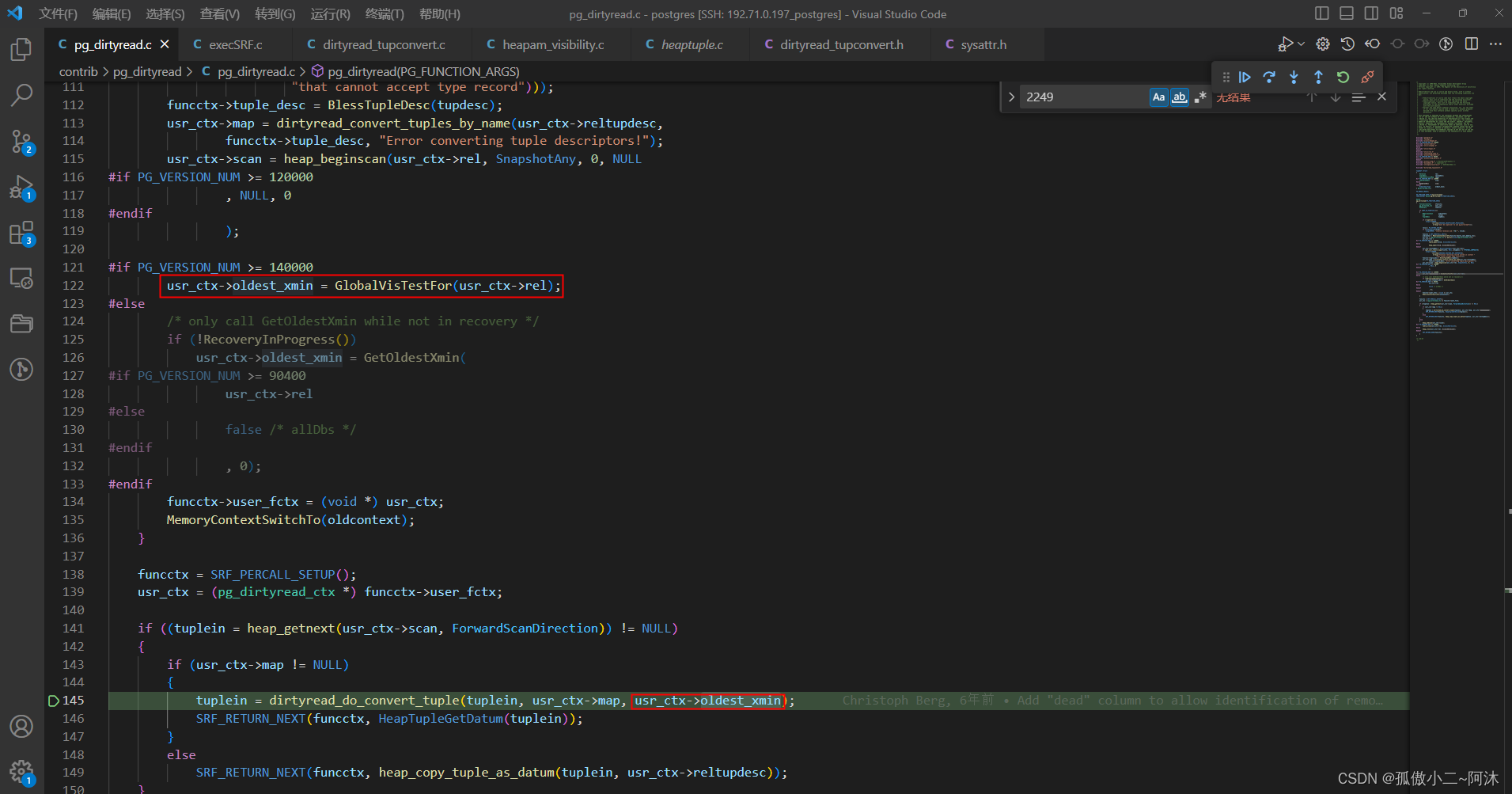
PostgreSQL的学习心得和知识总结(一百二十三)|深入理解PostgreSQL数据库开源扩展pg_dirtyread的使用场景和实现原理
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《PostgreSQL数据库内核分析》 2、参考书籍:《数据库事务处理的艺术:事务管理与并发控制》 3、PostgreSQL数据库仓库…...
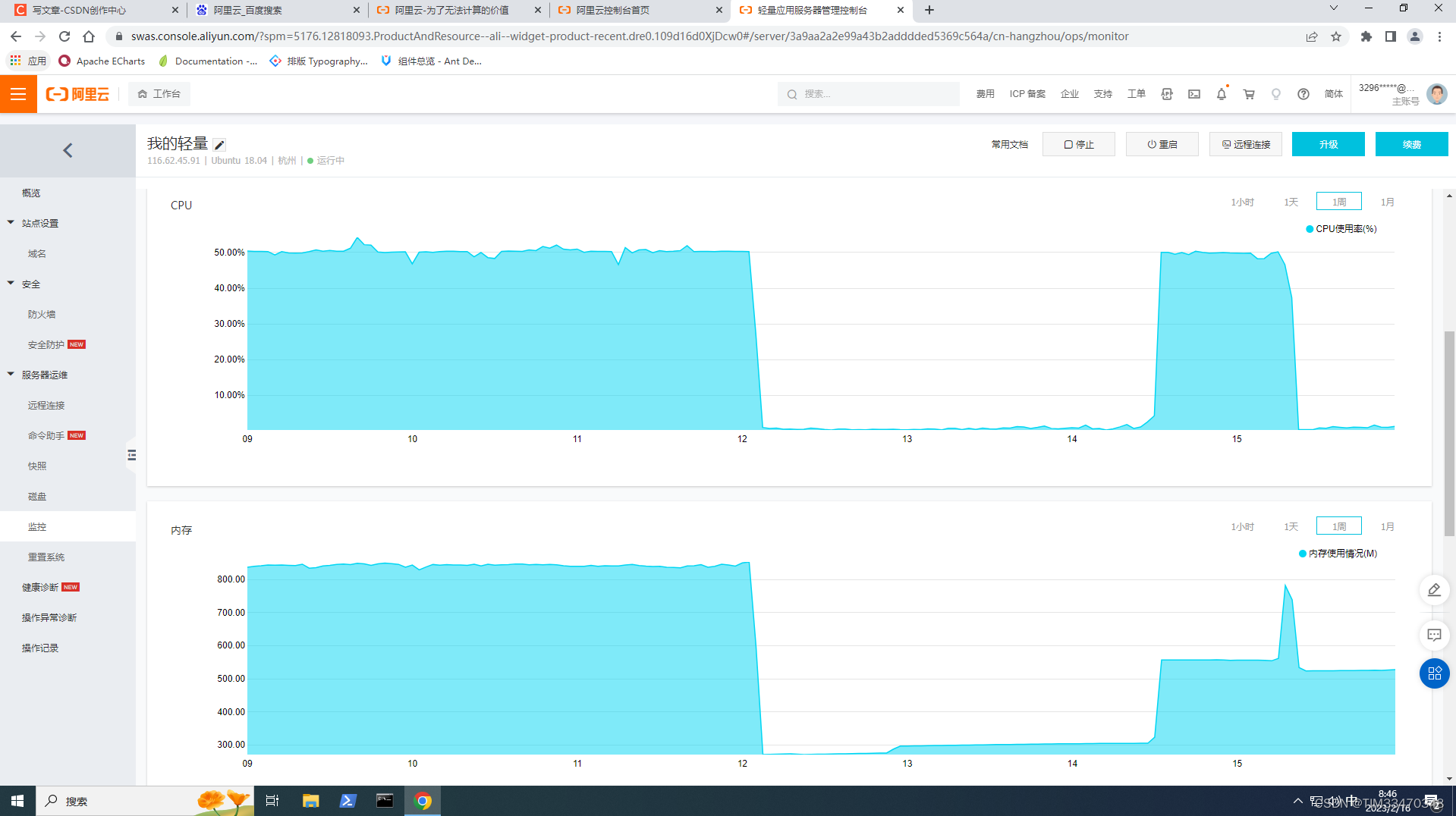
ubuntu清理挖矿病毒
0 序言 我之前搭建的hadoop用于测试,直接使用了8088和9870端口,没有放入docker,从而没有端口映射。于是,就被不法之徒盯上了,hadoop被提交了很多job,使得系统被感染了挖矿病毒,在前几天阿里云站…...

【代码随想录训练营】【Day16】第六章|二叉树|104.二叉树的最大深度|559.n叉树的最大深度|111.二叉树的最小深度|222.完全二叉树的节点个数
二叉树的最大深度 题目详细:LeetCode.104 递归法很容易理解: 定义一个全局变量max, 记录二叉树的最大深度在递归函数中增加一个深度参数,表示当前的节点的深度然后对二叉树进行深度优先遍历当遍历到叶子节点时,比较…...
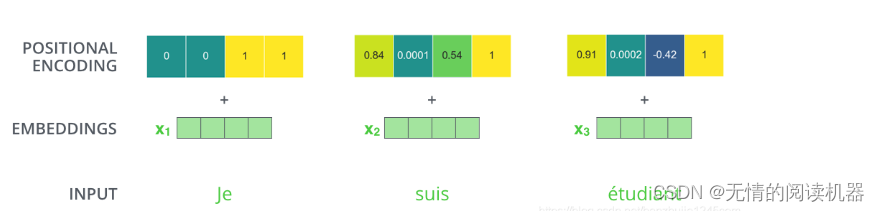
transformer总结
1.注意力机制 意义:人类的注意力机制极大提高了信息处理的效率和准确性。 公式: 1)自注意力机制 b都是在考虑了所有a的情况下生成的。 以产生b1向量为例: 1.在a这个序列中,找到与a1相关的其他向量 2.每个向量与a1关联的程度&a…...

dart flutter入门教程,开发手册 分享
我最近在学校dart flutter.这是我收集的一些手册和教程. 不需要关注公众号,不需要加好友. 我发现flutter(dart)的中文资料比较奇缺.入门的教程非常多.但是api手册几乎没有(全是英文的). 收集原则 1.中文(我英文不好) 2.不要pdf的,网上有一些pdf的 从入门到进阶的,但是太长…...

教育舆情监测关键词有哪些,TOOM教育舆情监测系统流程?
教育舆情监测是指对教育领域的舆情进行收集、分析和处理的过程。舆情是指公众在各种渠道上对教育政策、教育机构、教育事件等方面的言论、态度和情绪。通过对教育舆情的监测和分析,可以了解公众对教育行业的看法和反应,提高对教育行业的管控能力…...
MySQL高级(一)
MySQL-day01 1 MySQL简介 1.1 MySQL简介 MySQL是一个关系型数据库管理系统,由瑞典MySQL AB(创始人Michael Widenius)公司开发,2008被Sun收购(10亿美金),2009年Sun被Oracle收购。MariaDBMaria…...
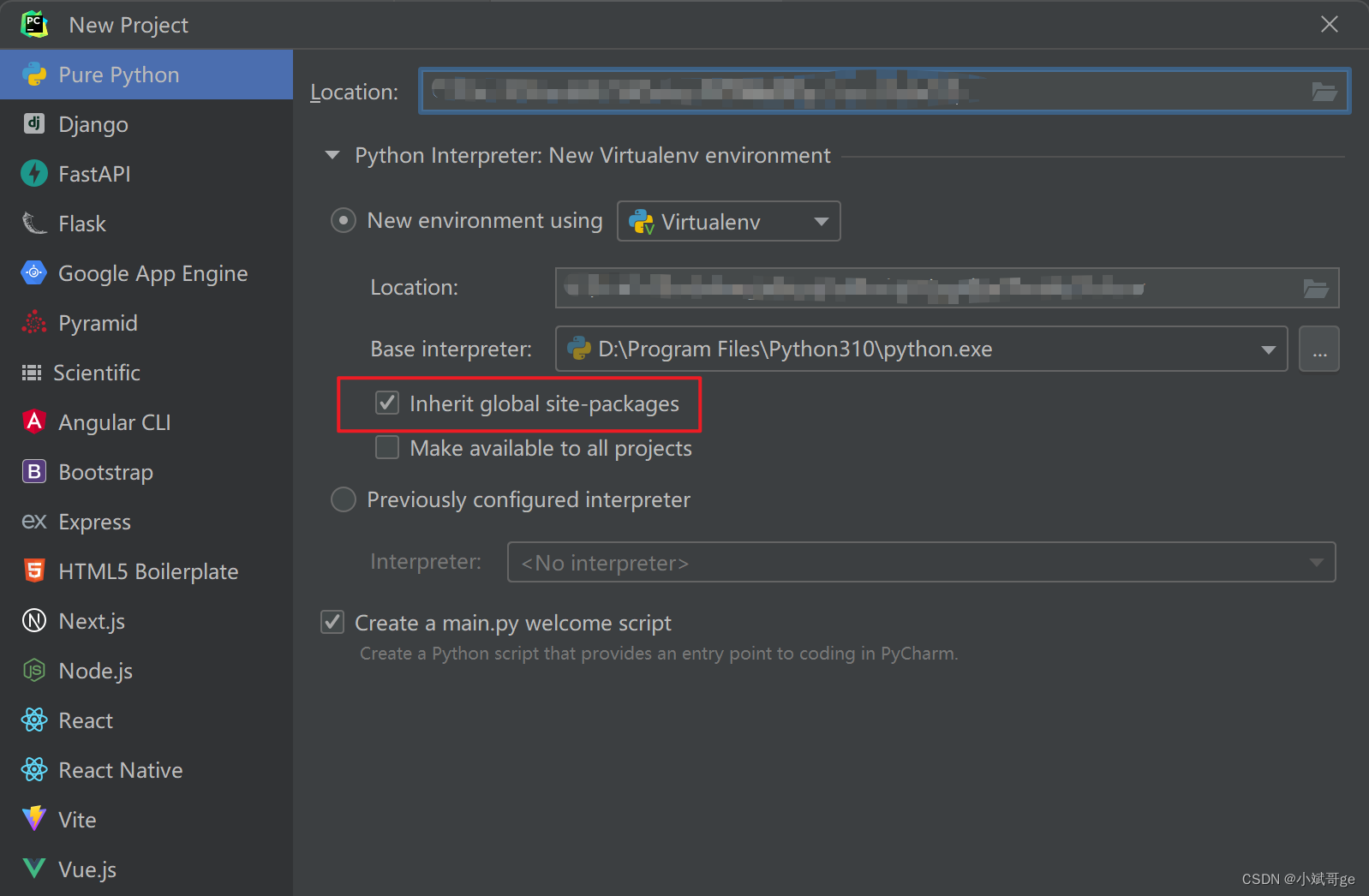
如何将Python项目部署到新电脑上运行?
如何将Python项目部署到新电脑上运行? 在工作中,可能需要在新服务器上部署项目代码,例如新增服务器、把测试环境的代码部署到生产环境等。 在生活中,也会遇到换新电脑,需要将自己在旧电脑上写的(项目&…...
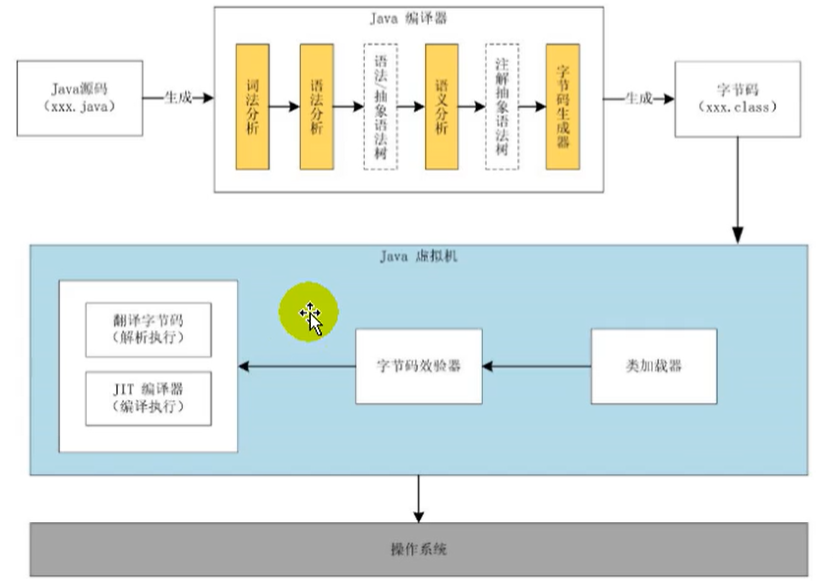
JVM和JAVA体系结构
1、为什么要学习JVM作为Java工程师的你曾被伤害过吗?你是否也遇到过这些问题?运行着的线上系统突然卡死,系统无法访问,甚至直接OOM想解决线上JVM GC问题,但却无从下手新项目上线,对各种JVM参数设置一脸茫然…...
(十)、通过云对象修改阅读量+点赞功能的实现【uniapp+uinicloud多用户社区博客实战项目(完整开发文档-从零到完整项目)】
1,通过云对象importObj修改阅读量 1.1 新建云对象 1.2 云对象中写自增自减方法 封装云对象utilsObj中的自增自减方法,方法名取为operation,传递4个参数。 // 云对象教程: https://uniapp.dcloud.net.cn/uniCloud/cloud-obj // jsdoc语法提…...
)
刷力扣的第一天脑子要长出来的感觉(怎么有人大四才开始啊啊啊啊啊啊啊啊啊啊啊啊,又是等成绩的一天,)
刷力扣的第一天脑子要长出来的感觉(为什么大四才开始啊啊啊啊啊啊啊啊啊啊啊啊) emmm,自己还是想不太出来(只是一点想法),可能还是会参考评论区,求各位轻喷 分析:带符号一定不是回…...
Nuclei文*件上*传FUZZ POC
目录 1.前言 2. Nuclei文件上传FUZZ POC 3. 实战中的应用 1.前言 该文件上传FUZZ POC主要来源于一个靶*场,该POC 主要用来FUZZ目标js页面中的upload ajax请求,以此来进一步尝试文件上传漏*洞利*用。 这里也要感谢下“打工仔1号”提供的开*发人员常见的文*件上*传javaScr…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...
