PTA L1-049 天梯赛座位分配(详解)
前言:内容包括:题目,代码实现,大致思路,代码解读
题目:
天梯赛每年有大量参赛队员,要保证同一所学校的所有队员都不能相邻,分配座位就成为一件比较麻烦的事情。为此我们制定如下策略:假设某赛场有 N 所学校参赛,第 i 所学校有 M[i] 支队伍,每队 10 位参赛选手。令每校选手排成一列纵队,第 i+1 队的选手排在第 i 队选手之后。从第 1 所学校开始,各校的第 1 位队员顺次入座,然后是各校的第 2 位队员…… 以此类推。如果最后只剩下 1 所学校的队伍还没有分配座位,则需要安排他们的队员隔位就坐。本题就要求你编写程序,自动为各校生成队员的座位号,从 1 开始编号。
输入格式:
输入在一行中给出参赛的高校数 N (不超过100的正整数);第二行给出 N 个不超过10的正整数,其中第 i 个数对应第 i 所高校的参赛队伍数,数字间以空格分隔。
输出格式:
从第 1 所高校的第 1 支队伍开始,顺次输出队员的座位号。每队占一行,座位号间以 1 个空格分隔,行首尾不得有多余空格。另外,每所高校的第一行按“#X”输出该校的编号X,从 1 开始。
输入样例:
3
3 4 2
输出样例:
#1
1 4 7 10 13 16 19 22 25 28
31 34 37 40 43 46 49 52 55 58
61 63 65 67 69 71 73 75 77 79
#2
2 5 8 11 14 17 20 23 26 29
32 35 38 41 44 47 50 53 56 59
62 64 66 68 70 72 74 76 78 80
82 84 86 88 90 92 94 96 98 100
#3
3 6 9 12 15 18 21 24 27 30
33 36 39 42 45 48 51 54 57 60代码实现:
#include<stdio.h>
int main()
{int n = 0;scanf("%d", &n);int num[101] = { 0 };int i = 0;int max = 0;int id = 0;int pos[101][11][11] = { 0 };int pre = 0;//输入各高校队伍数并求出最大的队伍数for (i = 1; i <= n; i++){scanf("%d", &num[i]);max = num[i] > max ? num[i] : max;}//编号int j = 0;for (j = 1; j <= max; j++){int k = 0;for (k = 1; k <= 10; k++){for (i = 1; i <= n; i++){if (j <= num[i]){//同一个学校隔位坐if (pre == i){id += 2;}else{//不同学校正常坐id += 1;}pre = i;pos[i][j][k] = id;}}}}//打印编号信息for (i = 1; i <= n; i++){printf("#%d\n", i);for (j = 1; j <= num[i]; j++){int k = 0;for (k = 1; k <= 10; k++){if (k != 10){printf("%d ", pos[i][j][k]);}else{printf("%d\n", pos[i][j][k]);}}}}return 0;
}大致思路:
1. 使用三维数组记录:每一个学校编号,每一个学校分配到的编号
注:每一个学校分配到的编号可以看成一个二维数组,行是该学校队伍的支数,列是一队的人数10
2. 分配编号: 以输入3
3 4 2 为例
a. 分成最大队伍数轮
分成四轮:第一轮给所有学校的第一支队伍分配编号
第二轮给所有学校的第二支队伍分配编号(若是有2支队伍)
第三轮给所有学校的第三支队伍分配编号(若是有3支队伍)
第四轮给所有学校的第四支队伍分配编号(若是有4支队伍)
b. 每一轮:给所有学校的某一支队伍的10个位置编号
现有3个学校,学校编号为1,2,3
学校1:3支队伍,编号的二维数组,行为3,列为10
学校2:4支队伍,编号的二维数组,行为4,列为10
学校3:2支队伍,编号的二维数组,行为2,列为10
c. 若是当前进行分配编号的学校与上一个分配编号的学校不同,则正常编号
若是相同,则隔位编号
代码解读:
part 1:
//输入各高校队伍数并求出最大的队伍数for (i = 1; i <= n; i++){scanf("%d", &num[i]);max = num[i] > max ? num[i] : max;}所有学校的最大队伍数存储到max中
part 2:
//编号int j = 0;for (j = 1; j <= max; j++){int k = 0;for (k = 1; k <= 10; k++){for (i = 1; i <= n; i++){if (j <= num[i]){//同一个学校隔位坐if (pre == i){id += 2;}else{//不同学校正常坐id += 1;}pre = i;pos[i][j][k] = id;}}}}1 编号的进行可以看成一个二维数组:行是最大队伍数(保证所有学校都能分配到编号),列是10
2 第一个for循环进行max次,每一次都给所有学校的某一支队伍(10个位置)编号
编号之前需要判断当前的轮(代表所有学校要进行编号的第x支队伍)是否小于等于当前分配编号的学校的队伍数
若是满足条件,则可以编号
若是大于,则不进行编号,因为当前要分配编号的学校没有这支队伍的位置
3 若是当前进行分配编号的学校与上一个分配编号的学校不同,则正常编号
若是相同,则隔位编号
以如下案列为例:
输入样例:
3
3 4 2
输出样例:
#1
1 4 7 10 13 16 19 22 25 28
31 34 37 40 43 46 49 52 55 58
61 63 65 67 69 71 73 75 77 79
#2
2 5 8 11 14 17 20 23 26 29
32 35 38 41 44 47 50 53 56 59
62 64 66 68 70 72 74 76 78 80
82 84 86 88 90 92 94 96 98 100
#3
3 6 9 12 15 18 21 24 27 30
33 36 39 42 45 48 51 54 57 60总共进行4次循环,因为最大队伍数是4
第一次循环:给学校1,学校2,学校3的第一支队伍的10个位置分配编号
第二次循环:给学校1,学校2,学校3的第二支队伍的10个位置分配编号
第三次循环:给学校1,学校2,学校3的第三支队伍的10个位置分配编号
第四次循环:给学校1,学校2,学校3的第四支队伍的10个位置分配编号
但是:学校1能分配编号的共3支队伍,学校2能分配编号的共4支队伍,学校3能分配编号的共2支队伍,即学校1和2能够进行3轮,给自己的1,2,3的队伍编号,只有学校4能够进行第4轮给自己的第四支队伍编号 ,学校3只能进行两轮给自己的1,2的队伍编号
故而我们在编号之前需要进行判断:
if (j <= num[i])j可以想象成二维数组的行,可以代表第几支队伍
相关文章:
)
PTA L1-049 天梯赛座位分配(详解)
前言:内容包括:题目,代码实现,大致思路,代码解读 题目: 天梯赛每年有大量参赛队员,要保证同一所学校的所有队员都不能相邻,分配座位就成为一件比较麻烦的事情。为此我们制定如下策…...

Linux部分参数作用讲解
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...

Java kafka
JAVA面试题--Kafka(最新最全) 目录概述需求:设计思路实现思路分析1.URL管理2.网页下载器3.爬虫调度器4.网页解析器5.数据处理器拓展实现性能参数测试:参考资料和推荐阅读)Survive by day and develop by night. talk for import b…...

DBA之路---Stream数据共享同步机制与配置方法
oracle的Stream解析–数据共享 在g版本常用,如果是c版本项目一般都会选择goldengate,比stream靠谱多了 Oracle中的stream是消息队列一种应用形式,原理如下: 收集oracle中的事件,将事件保存在队列里,然后将…...

CF1790E Vlad and a Pair of Numbers 题解
CF1790E Vlad and a Pair of Numbers 题解题目链接字面描述题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1思路代码实现题目 链接 https://www.luogu.com.cn/problem/CF1790E 字面描述 题面翻译 共有 ttt 组数据。 每组数据你会得到一个正整数 xxx&…...

漏洞预警|Apache Kafka Connect JNDI注入漏洞
棱镜七彩安全预警 近日网上有关于开源项目Apache Kafka Connect JNDI注入漏洞,棱镜七彩威胁情报团队第一时间探测到,经分析研判,向全社会发起开源漏洞预警公告,提醒相关安全团队及时响应。 项目介绍 Karaf是Apache旗下的一个开…...

企业小程序开发步骤【教你创建小程序】
随着移动互联网的兴起,微信已经成为了很多企业和商家必备的平台,而其中,微信小程序是一个非常重要的工具。本文将为大家介绍小程序开发步骤,教你创建小程序。 步骤一、注册小程序账号 先准备一个小程序账号,在微信公…...

刚性电路板的特点及与柔性电路板的区别
打开市场上的任何一个电子产品,会发现里面都有一块或多块电路板。电路板是电子产品运行的核心,之前沐渥小编已经给大家介绍了柔性电路板,下面给大家介绍刚性电路板的基础知识。 刚性电路板俗称硬板,是由不容易变形的刚性基材制成的…...

扫码过磅+车牌识别,内蒙古蒙维过磅实现信息化管理
扫码过磅、车牌识别、对接SAP ERP系统设计思路: 无人值守系统升级改造包括车牌自动识别系统、信息化(扫码等方式)管理系统、智能自动控制系统等实现信息无纸化传递。远程监管地点设于公司东磅房,可以实现远程监测监控画面、称重过…...
蒙特卡洛计算圆周率
使用MC计算圆周率的小例子,使用python的numpy,matplotlib库import numpy as npimport matplotlib.pyplot as pltdef mc_calculate_pi(t):np.random.seed(t)rand_num np.random.rand(t)rand_num2 np.random.rand(t)l1 rand_num-0.5l2 rand_num2-0.5l0…...
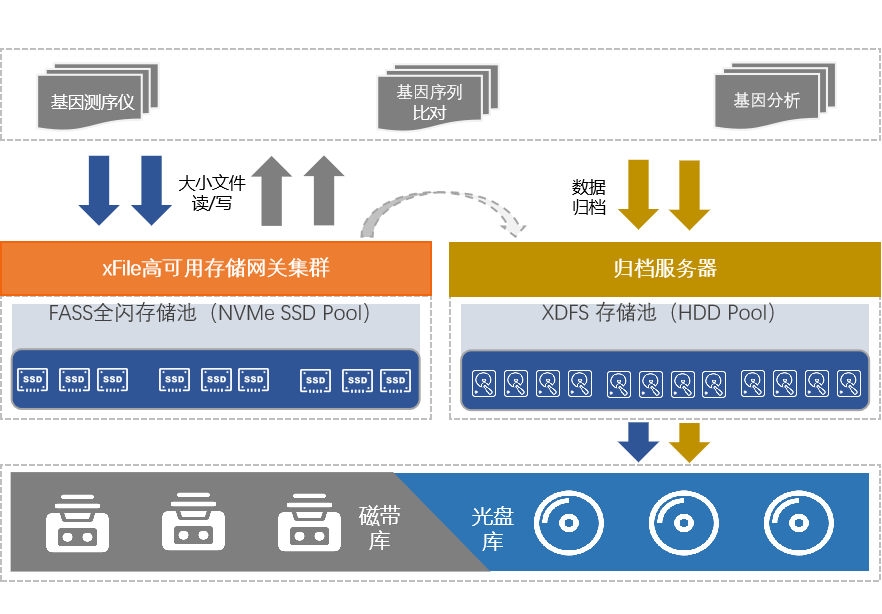
生物信息场景下的用户需求
背景分析概念定义基因测序是一种新型基因检测技术,是基因检测的方法之一,其又叫基因谱测序,是国际上公认的一种基因检测标准。基因测序技术能锁定病变基因,提前预防和治疗。过长的测序周期以及上万美元的仪器成本,成了…...
和sudo(superuser do)的区别?(sudo su与su的区别))
linux su(switch user)和sudo(superuser do)的区别?(sudo su与su的区别)
文章目录linux su(switch user)和sudo(superuser do)的区别?sudo su与su的区别linux su(switch user)和sudo(superuser do)的区别? 在Unix或Linux操作系统中…...
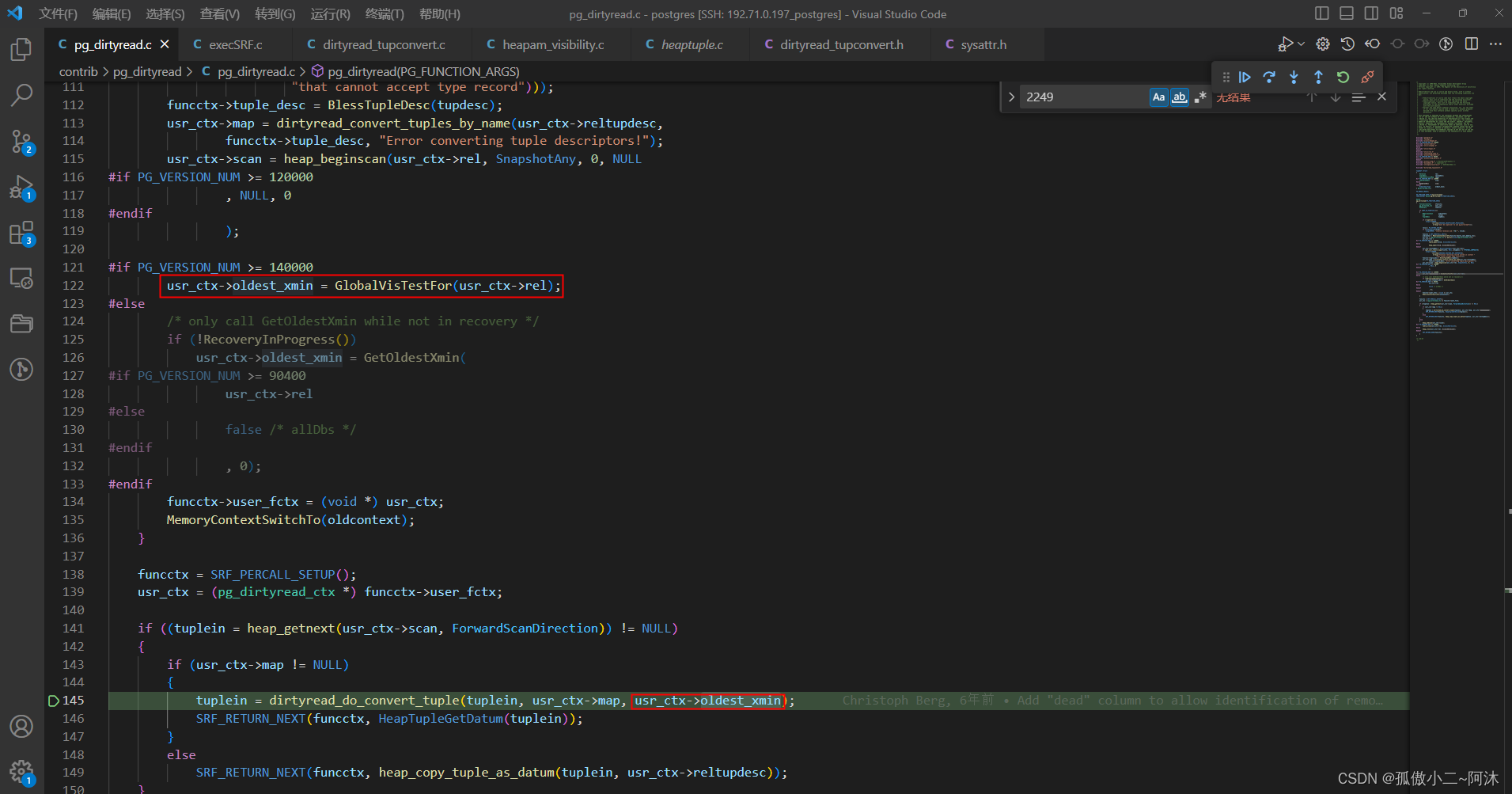
PostgreSQL的学习心得和知识总结(一百二十三)|深入理解PostgreSQL数据库开源扩展pg_dirtyread的使用场景和实现原理
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《PostgreSQL数据库内核分析》 2、参考书籍:《数据库事务处理的艺术:事务管理与并发控制》 3、PostgreSQL数据库仓库…...
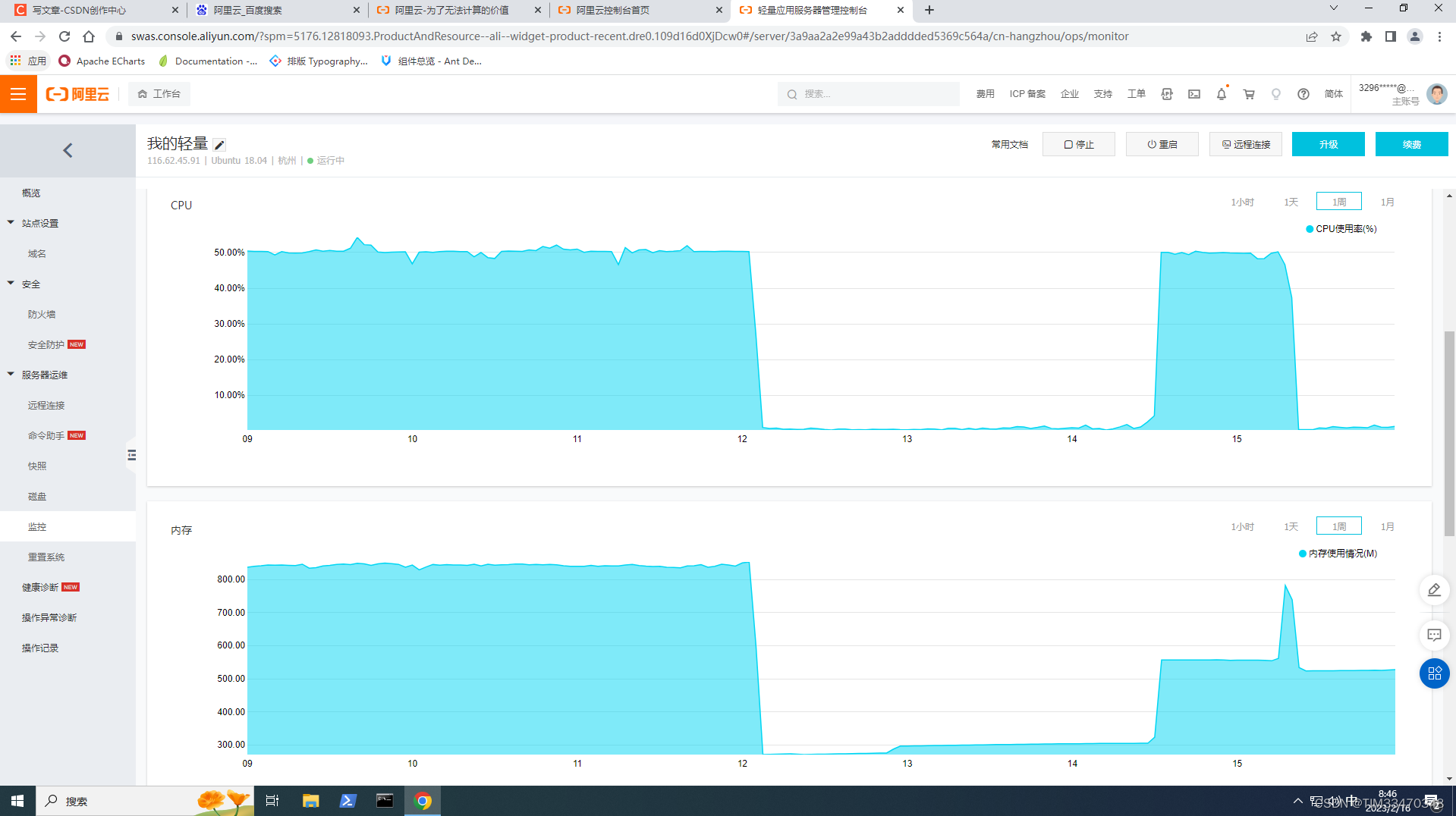
ubuntu清理挖矿病毒
0 序言 我之前搭建的hadoop用于测试,直接使用了8088和9870端口,没有放入docker,从而没有端口映射。于是,就被不法之徒盯上了,hadoop被提交了很多job,使得系统被感染了挖矿病毒,在前几天阿里云站…...

【代码随想录训练营】【Day16】第六章|二叉树|104.二叉树的最大深度|559.n叉树的最大深度|111.二叉树的最小深度|222.完全二叉树的节点个数
二叉树的最大深度 题目详细:LeetCode.104 递归法很容易理解: 定义一个全局变量max, 记录二叉树的最大深度在递归函数中增加一个深度参数,表示当前的节点的深度然后对二叉树进行深度优先遍历当遍历到叶子节点时,比较…...
transformer总结
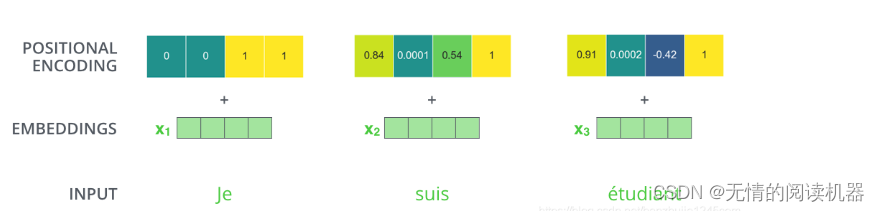
1.注意力机制 意义:人类的注意力机制极大提高了信息处理的效率和准确性。 公式: 1)自注意力机制 b都是在考虑了所有a的情况下生成的。 以产生b1向量为例: 1.在a这个序列中,找到与a1相关的其他向量 2.每个向量与a1关联的程度&a…...

dart flutter入门教程,开发手册 分享
我最近在学校dart flutter.这是我收集的一些手册和教程. 不需要关注公众号,不需要加好友. 我发现flutter(dart)的中文资料比较奇缺.入门的教程非常多.但是api手册几乎没有(全是英文的). 收集原则 1.中文(我英文不好) 2.不要pdf的,网上有一些pdf的 从入门到进阶的,但是太长…...

教育舆情监测关键词有哪些,TOOM教育舆情监测系统流程?
教育舆情监测是指对教育领域的舆情进行收集、分析和处理的过程。舆情是指公众在各种渠道上对教育政策、教育机构、教育事件等方面的言论、态度和情绪。通过对教育舆情的监测和分析,可以了解公众对教育行业的看法和反应,提高对教育行业的管控能力…...
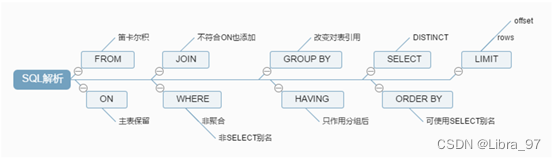
MySQL高级(一)
MySQL-day01 1 MySQL简介 1.1 MySQL简介 MySQL是一个关系型数据库管理系统,由瑞典MySQL AB(创始人Michael Widenius)公司开发,2008被Sun收购(10亿美金),2009年Sun被Oracle收购。MariaDBMaria…...
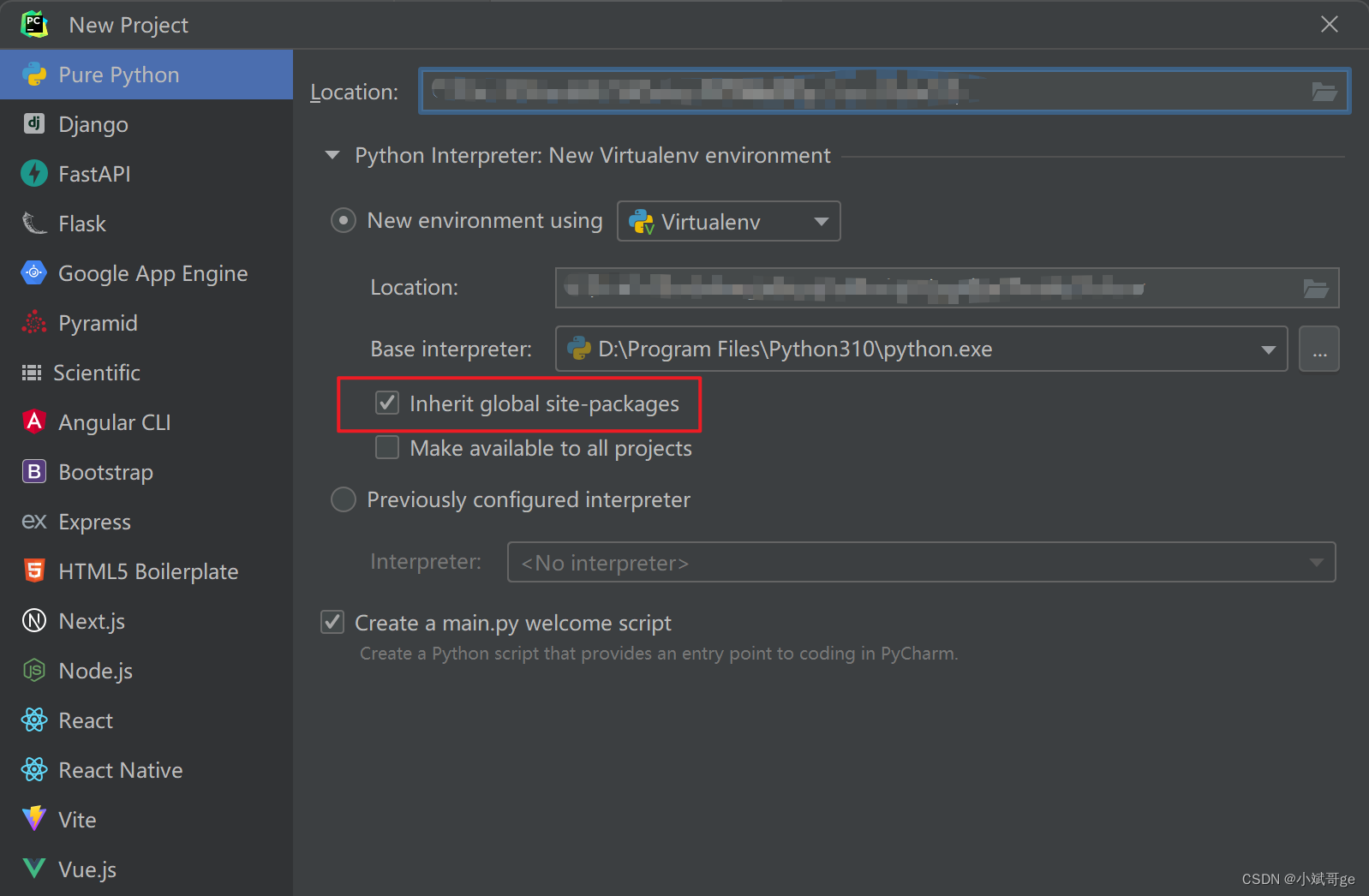
如何将Python项目部署到新电脑上运行?
如何将Python项目部署到新电脑上运行? 在工作中,可能需要在新服务器上部署项目代码,例如新增服务器、把测试环境的代码部署到生产环境等。 在生活中,也会遇到换新电脑,需要将自己在旧电脑上写的(项目&…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...
