线性基 学习笔记
什么是线性基?
先来回顾一下向量空间中的基。这个基代表着空间的一个极大线性无关子集,组中向量线性无关,且空间中的任意一个向量都可以唯一地由基中的向量来表示
那么回到线性基,它其实就类似于是一个向量空间的基
我们考虑一个问题:给定一个数组a,要求一个最小的数组d,使得a中的任意一个数可以由d中的若干个数字来通过异或得到,且d中任意多个数字的异或结果不为0
注意到异或操作其实就是在模2意义下的加法操作,我们如果将每一个数字按二进制位分解,就可以看成一个n维向量(我们假定数字<=2^n)
所以当前要求的东西如下:
给定一个向量组a,,求一组向量d,
(向量个数为m),使得
,存在唯一的一组解k满足
(加法在模2意义下),且不存在一组解s,使得
.
这里
(事实上这样一个线性基不一定是原数组的子集,但是略去这一点的话,它跟空间中的基的概念就有诸多相像的地方了。
这里列出对应的性质
1.数组中的任意一个数可以唯一地由线性基中的若干元素异或得到
2.线性基中任意多个元素的异或值不为0
3.线性基元素的异或集合等于原数组元素的异或集合
那么我们考虑一下如何求出这样一个集合并满足上述性质
好吧其实我也不知道前人是怎么搞出来这个东西的,但是可以意会一下
异或中一个极好的思考角度就是从二进制位入手。想要得到一个数字,说白了就是要让对应位为1或0.那么如果我们的线性基中,每一个数字都有一位,满足其它数字在这一位上都是0,那么或许就可以操控了。所以线性基其实就是按位分成n个数字,每一位对应一个数字(或许没有)
这里先给出求线性基的代码,再慢慢讲解(很简单的,别走)
void add(ll x)
{for(int i=63;i>=0;--i){if(x&(1ll<<i)){if(d[i]) x^=d[i];else {d[i]=x;break;} } }
}这是一个将元素尝试添加进线性基的代码。我们的操作就是,让线性基中每一个元素的最高位拥有唯一的1,就没了。这里如果一个数组的某一个1位已经存在对应的线性基元素了,我们直接将其取异或,知道它的最高位1是唯一的。如果没有这样的位,也就是最后x=0,就无法加入线性基
为什么这样是合理的?我们一个性质一个性质来看
不妨先看性质2 线性基中任意多个元素的异或值不为0
我们假设d[a]^d[b]^d[c]=0,并假设三者加入线性基的次序是a,b,c
显然d[a]^d[b]=d[c],所以在c尝试加入线性基的时候,就会加入失败。
得证
再看性质1 数组中的任意一个数可以唯一地由线性基中的若干元素异或得到
先考虑可行性:
假设数字A成功加入线性基的第i个位置
那么A^d[a]^d[b]^...^d[c]=d[i],反过来:A=d[a]^d[b]^...^d[c]^d[i].
如果A没有加入线性基
那就是因为线性基中存在一些数字的异或和=A
得证
再考虑唯一性:
如果存在两种方案使得d[a1]^d[a2]^..d[ai]=d[b1]^d[b2]^..d[bj]=A,那么取d[a1]^d[a2]^..d[ai]^d[b1]^d[b2]^..d[bj]=0,与性质2矛盾
得证
性质3 线性基元素的异或集合等于原数组元素的异或集合
线性基中的元素都是原数组元素互相异或得来的,所以该性质显然
所以说这样构造是合理的,其实就是按位贪心。
然后我们考虑一下用处:
求数组异或最大值
ans=0;
for(int i=60;i>=0;--i)
{ans=max(ans,ans^d[i]);
}其实还是按位贪心,如果高位能取到1的话,就取,因为决策具有单调性。
求数组异或最小值
如果有元素不能插入线性基,那么最小值显然就是0,否则就是线性基里最小的元素,因为最小的元素无论异或谁都会变大
求数组异或的第k小
我们考虑将线性基重新构造,使得每一个数字的每一位1都是唯一的
如果i<j,aj的第i位是1,就将aj异或上ai。
这样,我们只需要将k按二进制拆分,对于1的位,就异或上对应的元素即可
例题
板子
求数组异或最大值
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,k;
ll mas[N];
ll d[70];
void add(ll x)
{for(int i=60;i>=0;--i){if(x&(1ll<<i)){if(d[i]) x^=d[i]; else{d[i]=x;break;}}}
}
void solve()
{cin>>n;for(int i=1;i<=n;++i) cin>>mas[i];for(int i=1;i<=n;++i) add(mas[i]);ll ans=0;for(int i=60;i>=0;--i){ans=max(ans,ans^d[i]);}cout<<ans<<endl;
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);//ll t;cin>>t;while(t--)solve();return 0;
}彩灯
大意:
求数组的异或结果的种类数
思路:
我们考虑性质2,显然线性基中不同元素的异或结果一定不同,所以答案就是2^(线性基大小)
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,m;
string s;
ll d[70];
vector<ll> vt;
void add(ll x)
{for(int i=60;i>=0;--i){if(x&(1ll<<i)){if(d[i]) x^=d[i];else{d[i]=x;break;}}}
}
void solve()
{cin>>n>>m;for(int i=1;i<=m;++i){cin>>s;ll cnt=0;for(int j=0;j<n;++j){cnt*=2ll;if(s[j]=='O') cnt++;}//cout<<cnt<<endl;vt.push_back(cnt);}for(auto i:vt) add(i);ll num=0;for(int i=0;i<=60;++i) if(d[i]>0) num++;ll ans=1;for(int i=1;i<=num;++i){ans=ans*2%2008;}cout<<ans<<endl;
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();return 0;
}元素
大意:
每一个元素有一个id和val,选择一个子集,任意多个id的异或结果不为0,且val最大
思路:
线性基中任意元素的异或结果不为0,所以其实就是要求一个val最大的线性基。那么我们只要按val倒序贪心即可
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,m;
struct ty
{ll num,val;
}mas[N],d[70];
bool cmp(ty a,ty b)
{return a.val>b.val;
}
void add(ty a)
{for(int i=60;i>=0;--i){if(a.num&(1ll<<i)){if(d[i].num){a.num^=d[i].num;// a.val+=d[i].val;}else {d[i]=a;break;}}}
}
void solve()
{cin>>n;for(int i=1;i<=n;++i){cin>>mas[i].num>>mas[i].val;}sort(mas+1,mas+1+n,cmp);for(int i=1;i<=n;++i) add(mas[i]);ll sum=0;
// cout<<"sdf "<<endl;
// for(int i=0;i<=60;++i) if(d[i].num) cout<<d[i].num<<" "<<d[i].val<<endl;
// cout<<endl;for(int i=0;i<=60;++i) sum+=d[i].val;cout<<sum<<endl;
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();return 0;
}新Nim游戏
大意:
(懒
思路:
Nim的一个结论就是元素异或和为0时,先手必败,否则先手必胜
所以当前先手的策略就是使得后手无论怎么拿,都不可能使元素异或和=0。也就是,我们要取尽可能少的数,使得局面成为一个线性基。因为总能构造出一个线性基(多了就拿掉呗),所以先手必胜
那么升序插入线性基即可
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,m;
ll mas[N];
ll d[70];
ll sum=0;
void add(ll x)
{ll pre=x;for(int i=60;i>=0;--i){if(x&(1ll<<i)){if(d[i]) x^=d[i];else{d[i]=x;break;}}}if(x==0) sum+=pre;
}
void solve()
{cin>>n;for(int i=1;i<=n;++i) cin>>mas[i];sort(mas+1,mas+1+n,greater<ll>());for(int i=1;i<=n;++i) add(mas[i]);cout<<sum<<endl;
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();return 0;
}最大XOR路径
大意:
给一个 n 个点 m 条边(权值为di)的无向有权图,可能有重边和子环。可以多次经过一条边,求1→n 的路径的最大边权异或和。
思路:
显然,一条边被走两次之后,贡献就是0,那么我们什么时候会这样做?当第二次经过时可以到达其它地方时
其实这里有一类边集是很特殊的,环。我们可以异或来得到整个环的值,再从起点出去,就类似于是一个额外贡献。
这启示我们,我们可以将图分为一个一个环和一条链。我们的主线是链,我们沿着链走,中间碰到有环可以走的话,我们可以走,也可以不走。那么就相当于求环的值的集合的一个线性基,然后求链的值与该线性基元素的异或的最大值即可。
这里还有两个问题:
1.从环回去要走重边,所以环的值要扣掉重边对应的部分
2.如何选择我们的主链?
事实上,如果有两条主链的话,就有了一个环
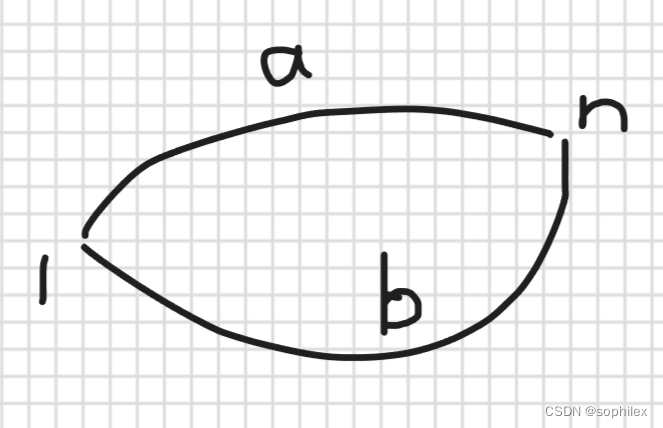
我们取价值为a的路,可能不如b优,但是环的价值是a^b,那么在最后的操作中,a^(a^b),就得到了b。所以我们其实可以任意选择一开始的主链。另外,选择不同的主链,最后可能会得到不同的一个一个的环。如何保证不同链能得到相同的环?不能保证,环套环的情况可能会导致不同的遍历顺序得到不同的环,但是简单环的异或操作可以得到所有的简单环。具体可以看一下这里
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,m;
struct ty
{ll t,l,next;
}edge[N<<1];
ll cn=0;
ll head[N];
ll res[N];
ll vis[N];
ll d[70];
void add(ll x)
{for(int i=63;i>=0;--i){if(x&(1ll<<i)){if(d[i]) x^=d[i];else {d[i]=x;break;} } }
}
ll ma(ll x)
{ll ans=x;for(int i=63;i>=0;--i){ans=max(ans,ans^d[i]);}return ans;
}
void add(ll a,ll b,ll c)
{edge[++cn].t=b;edge[cn].l=c;edge[cn].next=head[a];head[a]=cn;
}
void dfs(ll id,ll now)
{vis[id]=1;res[id]=now;for(int i=head[id];i!=-1;i=edge[i].next){ll y=edge[i].t;if(!vis[y]) dfs(y,now^edge[i].l);else add(now^edge[i].l^res[y]);}
}
void solve()
{memset(head,-1,sizeof head);cin>>n>>m;for(int i=1;i<=m;++i){ll a,b,c;cin>>a>>b>>c;add(a,b,c);add(b,a,c);}dfs(1,0);
// for(int i=64;i>=0;--i) if(d[i]) cout<<d[i]<<' ';
// cout<<endl;cout<<ma(res[n])<<endl;
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();return 0;
}Shortest Path Problem?
大意:
跟上一题一样,只是变成求路径异或最小值了
那么只是换个板子的事情
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n,m;
struct ty
{ll t,l,next;
}edge[N<<1];
ll cn=0;
ll head[N];
ll res[N];
ll vis[N];
ll d[70];
void add(ll x)
{for(int i=63;i>=0;--i){if(x&(1ll<<i)){if(d[i]) x^=d[i];else {d[i]=x;break;} } }
}
ll mi(ll x)
{ll ans=x;for(int i=63;i>=0;--i){ans=min(ans,ans^d[i]);}return ans;
}
void add(ll a,ll b,ll c)
{edge[++cn].t=b;edge[cn].l=c;edge[cn].next=head[a];head[a]=cn;
}
void dfs(ll id,ll now)
{vis[id]=1;res[id]=now;for(int i=head[id];i!=-1;i=edge[i].next){ll y=edge[i].t;if(!vis[y]) dfs(y,now^edge[i].l);else add(now^edge[i].l^res[y]);}
}
void solve()
{//1<<64就炸了 memset(head,-1,sizeof head);cin>>n>>m;for(int i=1;i<=m;++i){ll a,b,c;cin>>a>>b>>c;add(a,b,c);add(b,a,c);}dfs(1,0);
// for(int i=64;i>=0;--i) if(d[i]) cout<<d[i]<<' ';
// cout<<endl;cout<<mi(res[n])<<endl;
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();return 0;
}装备购买
大意:
求一组向量的极大无关组,其中每一个向量还有一个价值val,要求极大无关组的val总和最小
思路:
其实就是实数意义下的一个线性基。那么我们用高斯消元,像求线性基一样,如果当前最高位(向量最左边元素)没有对应的线性基,就加入,并更新后面对应的元素即可
至于val总和最小,跟之前一样,贪心即可
其实就是一个消元求解方程组的过程。
code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
#define ldb long double
const ldb eps=1e-7;
const ll N=510;
ll n,m;
struct ty
{ldb val[N];ldb cost;friend inline bool operator <(const ty& a,const ty& b){return a.cost<b.cost;}
}mas[N];
ll d[N];
ll cnt=0;
ldb ans=0;
void solve()
{cin>>n>>m;for(int i=1;i<=n;++i){for(int j=1;j<=m;++j) cin>>mas[i].val[j];}for(int i=1;i<=n;++i) cin>>mas[i].cost;sort(mas+1,mas+1+n);for(int i=1;i<=n;++i){for(int j=1;j<=m;++j){if(abs(mas[i].val[j])<eps) continue;if(!d[j]){d[j]=i;//确定对应的基ans+=mas[i].cost;cnt++;break;}ldb ap=mas[i].val[j]/mas[d[j]].val[j];for(int k=j;k<=m;++k){mas[i].val[k]-=ap*mas[d[j]].val[k];}}}cout<<cnt<<' '<<(ll)ans<<endl;
}
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();return 0;
}未完待续~
相关文章:

线性基 学习笔记
什么是线性基? 先来回顾一下向量空间中的基。这个基代表着空间的一个极大线性无关子集,组中向量线性无关,且空间中的任意一个向量都可以唯一地由基中的向量来表示 那么回到线性基,它其实就类似于是一个向量空间的基 我们考虑一…...

算法-回溯算法-组合问题
77. 组合https://leetcode.cn/problems/combinations/ 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。 示例 1: 输入:n 4, k 2 输出: [[2,4],[3,4],[2,3],[1,2],[1,3],[1,…...

ABAP中的Null值与space 以及 BW中ADSO的Key值
写出来怪丢人,到现在还没搞懂这个。 在BW中创建ADSO,定义Key字段。可以看到ADSO表的定义中,所有的Key和Data属性如下: 所有的key会有关键字key打头,所有字段都有not null. 但是并不是有个字段是blank空的就不能更新进…...

JavaScript库之Lodash常用方法
Lodash 中文文档https://www.lodashjs.com/docs/lodash.omit/以下总结了在项目中常用的方法,其他的慢慢更新语言:cloneDeep这个方法类似_.clone,除了它会递归拷贝 value。(注:也叫深拷贝)参数value (*): 要…...
Kotlin新手教程二(Kotlin基本数据类型及基础语法)
一、基本数据类型 1.数字 由于Kotlin支持类型推断,所以在使用时若超出Int的范围则会被认定为其它类型;若需要显式指定Long型值,则需要在值后添加L后缀。 2.浮点数 3.比较两个数( 和 ) Kotlin 中没有基础数据类型&a…...
git idea创建新分支,获取/合并主支代码的2个方法
其他sql格式也在更新中,可直接查看这个系列,要是没有你需要的格式,可在评论或私信我 个人目录 获取主支代码的2个方法1,创建一个分支,获取主支的所有代码(场景:我需要一个自己的分支进行编写模…...

CF1714A Everyone Loves to Sleep 题解
CF1714A Everyone Loves to Sleep 题解题目链接字面描述题面翻译题目描述输入格式输出格式样例解释题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1代码实现题目 链接 https://www.luogu.com.cn/problem/CF1714A 字面描述 题面翻译 题目描述 Vlad和其他人一样&am…...
oracle官方下载历史版本JDK版本
背景 日常工作中由于一些特殊原因,我们需要下载指定系统指定位数指定版本的jdk,这个时候去网上搜索下载就会遇到各种坑,病毒、诱导连接、诱导关注/注册、付费、错误版本等,所以最好的办法是去官网下载,下面列举两种方式…...

双击-jar包无法运行解决方法
我自己是通过探索出来的方法解决的,网上的方法适合普通问题 网络流传方法 那种-jar和run.bat的就是曲解了问题意思,问题不是如何运行,而是如何双击jar包就可以直接运行。 普通小问题就是修改注册表,将java路径写进去后面加个 %1…...
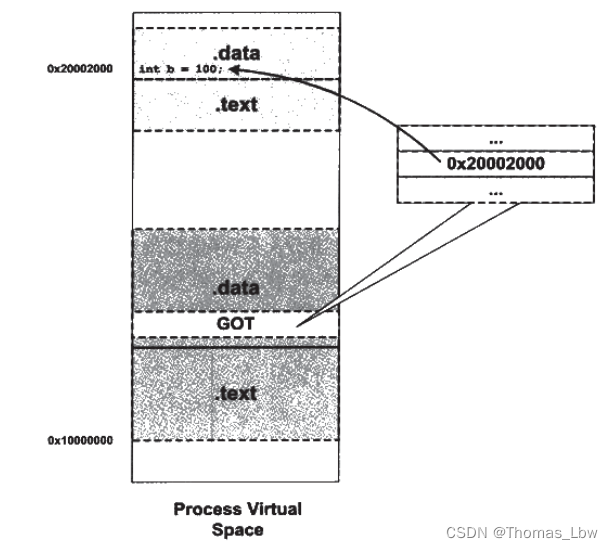
程序员的自我修养第七章——动态链接 (下)
接上一篇。 7.3 地址无关代码 对于现代机器来说,引入地址无关代码并不麻烦,我们展示下各种模型的地址引用方式: 1. 模块内部函数调用 2. 模块内部的数据访问,如全局变量、静态变量。 3. 模块外部的函数调用,跳转。 4.…...
蓝桥杯刷题——基础篇(二)
这部分题目,主要面向有志参加ACM与蓝桥杯竞赛的同学而准备的,蓝桥杯与ACM考察内容甚至评测标准基本都一样,因此本训练计划提供完整的刷题顺序,循序渐进,提高代码量,巩固基础。因竞赛支持C语言、C、Java甚至…...
)
PTA L1-049 天梯赛座位分配(详解)
前言:内容包括:题目,代码实现,大致思路,代码解读 题目: 天梯赛每年有大量参赛队员,要保证同一所学校的所有队员都不能相邻,分配座位就成为一件比较麻烦的事情。为此我们制定如下策…...

Linux部分参数作用讲解
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...

Java kafka
JAVA面试题--Kafka(最新最全) 目录概述需求:设计思路实现思路分析1.URL管理2.网页下载器3.爬虫调度器4.网页解析器5.数据处理器拓展实现性能参数测试:参考资料和推荐阅读)Survive by day and develop by night. talk for import b…...

DBA之路---Stream数据共享同步机制与配置方法
oracle的Stream解析–数据共享 在g版本常用,如果是c版本项目一般都会选择goldengate,比stream靠谱多了 Oracle中的stream是消息队列一种应用形式,原理如下: 收集oracle中的事件,将事件保存在队列里,然后将…...

CF1790E Vlad and a Pair of Numbers 题解
CF1790E Vlad and a Pair of Numbers 题解题目链接字面描述题面翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1思路代码实现题目 链接 https://www.luogu.com.cn/problem/CF1790E 字面描述 题面翻译 共有 ttt 组数据。 每组数据你会得到一个正整数 xxx&…...

漏洞预警|Apache Kafka Connect JNDI注入漏洞
棱镜七彩安全预警 近日网上有关于开源项目Apache Kafka Connect JNDI注入漏洞,棱镜七彩威胁情报团队第一时间探测到,经分析研判,向全社会发起开源漏洞预警公告,提醒相关安全团队及时响应。 项目介绍 Karaf是Apache旗下的一个开…...

企业小程序开发步骤【教你创建小程序】
随着移动互联网的兴起,微信已经成为了很多企业和商家必备的平台,而其中,微信小程序是一个非常重要的工具。本文将为大家介绍小程序开发步骤,教你创建小程序。 步骤一、注册小程序账号 先准备一个小程序账号,在微信公…...

刚性电路板的特点及与柔性电路板的区别
打开市场上的任何一个电子产品,会发现里面都有一块或多块电路板。电路板是电子产品运行的核心,之前沐渥小编已经给大家介绍了柔性电路板,下面给大家介绍刚性电路板的基础知识。 刚性电路板俗称硬板,是由不容易变形的刚性基材制成的…...

扫码过磅+车牌识别,内蒙古蒙维过磅实现信息化管理
扫码过磅、车牌识别、对接SAP ERP系统设计思路: 无人值守系统升级改造包括车牌自动识别系统、信息化(扫码等方式)管理系统、智能自动控制系统等实现信息无纸化传递。远程监管地点设于公司东磅房,可以实现远程监测监控画面、称重过…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...
