机器学习深度学习——线性回归的基本元素
回归用来表示输入输出之间的关系。
用实际例子来解释一下线性回归:根据房屋的面积、房龄来估算房屋价格。为了实现这个预测放假的模型,需要收集一个真实的数据集,该数据集包括了房屋的销售价格、面积和房龄。
在机器学习中,这个数据集称为训练集(training set),每行数据称为样本(sample)或数据点(data point),试图预测的目标称为标签(label)或目标(target)。预测所依据的自变量(面积和房龄)称为特征(feature)。
通常,我们使用n来表示数据集中的样本数。对索引为i的样本,其输入表示为:
x ( i ) = [ x 1 ( i ) , x 2 ( i ) ] T x^{(i)}=[x_1^{(i)},x_2^{(i)}]^T x(i)=[x1(i),x2(i)]T
其对应的标签是:
y ( i ) y^{(i)} y(i)
线性回归的基本元素
- 线性模型
- 损失函数
- 解析解
线性模型
p r i c e = w a r e a ⋅ a r e a + w a g e ⋅ a g e + b price=w_{area}·area+w_{age}·age+b price=warea⋅area+wage⋅age+b
其中,w为权重,决定了每个特征对我们预测值的影响。b为偏置,指当所有特征取0时的预测值。
严格来说,上式是输入特征的一种仿射变换,其特点是通过加权和特征进行线性变换,并通过偏置项来进行平移。
而在机器学习中,通常使用高维数据集,建模时采用线性代数表示法会比较方便。当我们的输入包含d个特征时,我们将预测结果表示为:
y ^ = w 1 x 1 + . . . + w d x d + b \hat{y}=w_1x_1+...+w_dx_d+b y^=w1x1+...+wdxd+b
将所有的特征放到向量x中,并将所有权重放到向量w中,可以用点积来简洁地表达模型:
y ^ = w T x + b \hat{y}=w^Tx+b y^=wTx+b
显然,向量x只能对应于单个数据样本的特征。
用符号表示的矩阵X可以很方便地引用我们整个数据集的n个样本。其中,X的每一行是一个样本,每一列是一种特征。
对于特征集合X,预测值可以通过矩阵-向量乘法表示为:
y ^ = X w + b \hat{y}=Xw+b y^=Xw+b
这个过程中的求和将使用广播机制,给定X和y,线性回归的目标就是找到一组权重向量w和偏置b:当给定从X的同分布中取样的新样本特征时,能使得新样本预测标签的误差尽可能小。
但即使确信特征与标签的潜在关系是线性的, 我们也会加入一个噪声项来考虑观测误差带来的影响。
因此,在开始寻找最好的模型参数w和b之前,还需要两个东西:
(1)一种模型质量的度量方式
(2)一种能够更新模型以提高模型预测质量的方法
损失函数
损失函数能够量化目标的实际值与预测值之间的差距。通常选择非负数作为损失,数值越小表示损失越小,完美预测的损失为0。
回归问题中最常用损失函数是平方误差函数:
l ( i ) ( w , b ) = 1 2 ( y ^ ( i ) − y ( i ) ) 2 l^{(i)}(w,b)=\frac{1}{2}(\hat{y}^{(i)}-y^{(i)})^2 l(i)(w,b)=21(y^(i)−y(i))2
常数1/2不会带来本质上的差别,但这样的形式会稍微简单一点(因为求导后常系数会变为1)。
由于平方误差函数中的二次方项,估计值和观测值之间较大的差异会导致更大的损失。为了度量模型在整个数据集上的质量,我们要计算在训练集n个样本上的损失均值(等价于求和):
L ( w , b ) = 1 n ∑ i = 1 n l ( i ) ( w , b ) = 1 n ∑ i = 1 n 1 2 ( w T x ( i ) + b − y ( i ) ) 2 L(w,b)=\frac{1}{n}\sum_{i=1}^nl^{(i)}(w,b) =\frac{1}{n}\sum_{i=1}^n{\frac{1}{2}(w^Tx^{(i)}+b-y^{(i)})^2} L(w,b)=n1i=1∑nl(i)(w,b)=n1i=1∑n21(wTx(i)+b−y(i))2
在训练模型时,希望寻找一组参数,这组参数能最小化在所有训练样本上的总损失。
解析解
线性回归是一个很简单的优化问题,线性回归的解可以用一个公式简单表达,这类解叫做解析解。
首先,将偏置b合并到参数w中,合并方法是在包含所有参数的矩阵中附加一列。我们的预测问题是最小化:
∣ ∣ y − X w ∣ ∣ 2 ||y-Xw||^2 ∣∣y−Xw∣∣2
这在损失平面上只有一个临界点,对应于整个取余的损失极小点。将损失关于w的导数设为0,得到解析解:
w ∗ = ( X T X ) − 1 X T y w^*=(X^TX)^{-1}X^Ty w∗=(XTX)−1XTy
但是解析解对问题限制太严格,不适合广泛应用于深度学习,接下来讲解随机梯度下降,几乎可以用来优化所有深度学习模型。
相关文章:

机器学习深度学习——线性回归的基本元素
回归用来表示输入输出之间的关系。 用实际例子来解释一下线性回归:根据房屋的面积、房龄来估算房屋价格。为了实现这个预测放假的模型,需要收集一个真实的数据集,该数据集包括了房屋的销售价格、面积和房龄。 在机器学习中,这个数…...
K8S初级入门系列之八-网络
一、前言 本章节我们将了解K8S的相关网络概念,包括K8S的网络通讯原理,以及Service以及相关的概念,包括Endpoint,EndpointSlice,Headless service,Ingress等。 二、网络通讯原理和实现 同一K8S集群&…...

分段@Transactional 坑及失效问题
Transactional 背景:在某些情况下,我们需要分段transaction,在最外面没有transaction,里面分成几个transaction,保证分段是成功的。 问题代码: Service public Order getOrder1(String id) {Optional<Or…...
25、matlab里面的10中优化方法介绍——Opt_Golden法(matlab程序)
1.简述 基本思想 黄金分割法也称为 0.618 法,其基本思想是通过取试探点和进行函数值比较,使包含极小点的搜索区间不断缩短以逼近极小值点。适用于确定区间上的任何单谷函数求极小值的问题。 公式推导 设有定义在[ a , b ] [a,b][a,b]上的单谷函数 φ ( …...

点云拟合球体
前言:在很多情况下,需要根据点云来拟合球体,本博文主要介绍各种方法的拟合情况及优缺点,希望对各位小伙伴有所帮助! 目录 1. vtkFitImplicitFunction进行球拟合 2. 四点求解球 1. vtkFitImplicitFunction进行球拟合 …...
算法的增程式EV能量管理策略研究(MATLAB编程))
基于动态规划(DP)算法的增程式EV能量管理策略研究(MATLAB编程)
文章目录 算法代码仿真结果结果分析算法代码 clc; clear; close all; load CWTVC.mat N=length(T_z); %N=200;load minFuelConsup.txt minFuel_Pe=minFuelConsup(:...

前端知识点视频补充
使用工具: Vscode使用: 需要下载插件:open in browser。这个插件可以快速打开浏览器。 选择文件夹有两种方式:选择打开文件、拖拽方式(这种最方便) 快捷键:快速生成Htm结构文件:…...

python多线程—终止子线程
总体思路 1、获取需要终止的子线程id 2、根据子线程id,终止子线程。 过程 获取子线程id: import threading Thread_id threading.get_ident() # 获取子线程的id值线程终止函数 def async_raise(Thread_id, exctype):"""raises th…...

#P1012. [NOIP2015提高组] 神奇的幻方
题目描述 幻方是一种很神奇的 N \times NNN 矩阵:它由数字 1,2,3, \ldots ,N \times N1,2,3,…,NN 构成,且每行、每列及两条对角线上的数字之和都相同。 当 NN 为奇数时,我们可以通过以下方法构建一个幻方: 首先将 11 写在第一行…...
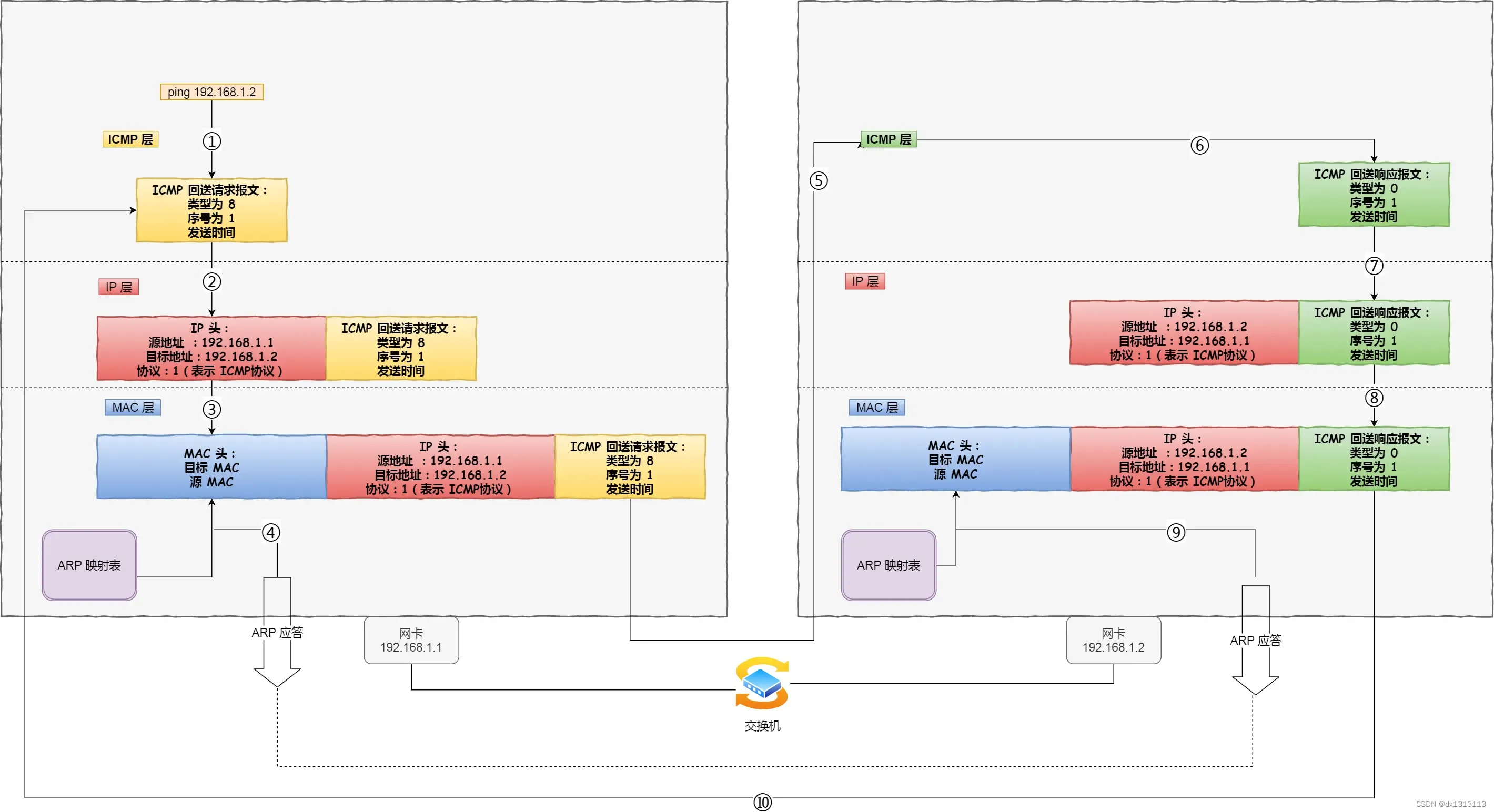
(学习笔记-IP)Ping的工作原理
Ping是基于ICMP协议工作的,ICMP报文封装在IP包里面,它工作在网络层,是IP协议的助手。 ICMP包头的类型字段,大致可分为两大类: 一类是用于诊断的查询消息,也就是查询报文类型一类是通知出错原因的错误消息&…...

php 进程间通信:管道、uds
1、管道 1.1、管道概念 管道是单向的、先进先出的,它把进程的输出和另一个进程的输入连接在一起。一个进程往管道写入数据,另一个进程从管道读取数据。数据被从管道中读取出来之后,将被删除,其他进程无法在读取到相应的数据。管…...

Stable Diffusion如何生成高质量的图-prompt写法介绍
文章目录 Stable Diffusion使用尝试下效果prompt的编写技巧prompt 和 negative promptPrompt格式Prompt规则细节优化Guidance Scale 总结 Stable Diffusion Stable Diffusion是一个开源的图像生成AI系统,由Anthropic公司开发。它基于 Transformer模型架构,可以通过文字描述生成…...

MySQL 高级SQL语句(一)
目录 一、高级SQL语句(进阶查询) 1.1 select 1.2 distinct 1.3 where 1.4 and 和 or 1.5 in 1.6 between 1.7 通配符 1.8 like 1.9 order by 一、高级SQL语句(进阶查询) 先准备2个表 一个location表: use m…...

SkyWalking链路追踪-技术文档首页
SkyWalking 文档中文版(社区提供) (skyapm.github.io)https://skyapm.github.io/document-cn-translation-of-skywalking/ SkyWalking-基本概念 SkyWalking链路追踪是一个用于分布式系统的性能监控工具,它帮助开发人员了解系统中各组件之间…...
AndroidStudio Memory profiler(内存分析器)
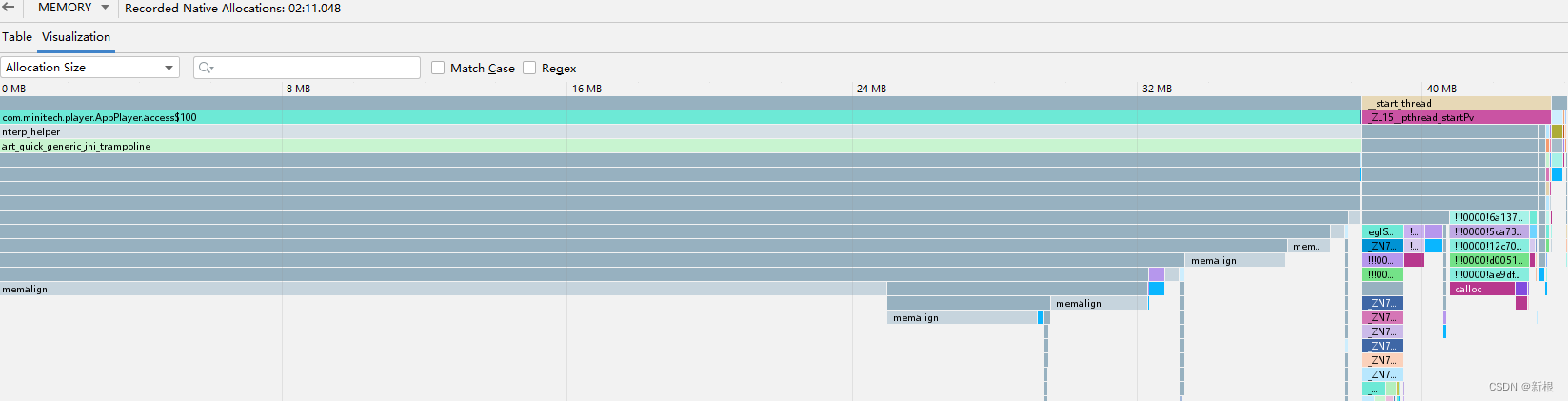
1.Record Java/Kotlin allocations 查看java 层中对象的调用栈和短时间内创建对象的次数。可用于内存抖动快速分析,可用快速查找到该对象的调用栈(等同于mat) 从上图可见,短时间内创建了23个char[] 数组,其中最大的char[] 占用20k, 查看cll stack 调用…...

【C++模板进阶】
目录 一、模板使用时的一个小注意点二、非类型模板参数三、类模板的特化3.1函数模板的特化3.2类模板的特化3.2.1全特化3.2.2偏特化 四、模板的分离编译4.1模板不支持分离编译4.2模板分离编译报错的分析4.2解决方案 五、模板的总结 一、模板使用时的一个小注意点 在使用模板时&…...
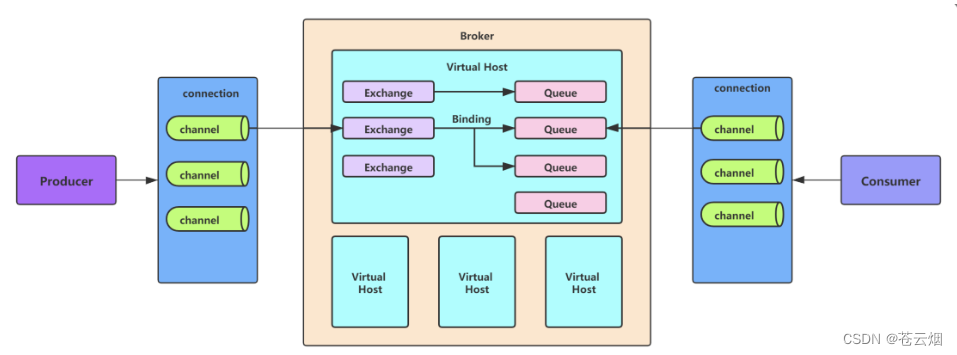
(一)RabbitMQ概念-优势、劣势、应用场景 、AMQP、工作原理
Lison <dreamlison163.com>, v1.0.0, 2023.06.22 RabbitMQ概念-优势、劣势、应用场景 、AMQP、工作原理 文章目录 RabbitMQ概念-优势、劣势、应用场景 、AMQP、工作原理RabbitMQ概念RabbitMQ的优势RabbitMQ劣势RabbitMQ应用的场景RabbitMQ_AMQPRabbitMQ工作原理 RabbitM…...
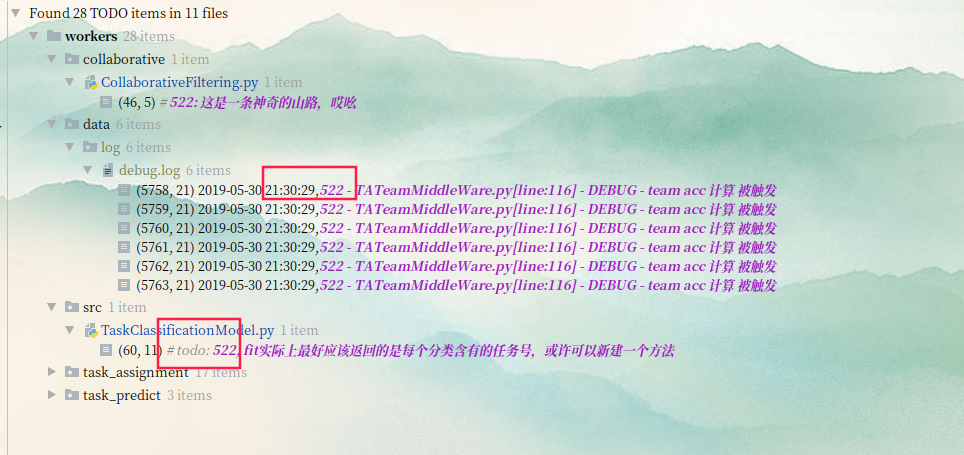
JetBrains全家桶:如何自定义实现类TODO注释?
文章目录 效果图具体方法参考文献 效果图 TODO注释大家应该都用过,在注释开头打上TODO的话,软件下方的TODO选项卡里就可以自动筛选出你打了TODO的注释,你可以点击里面对应的注释来实现快速跳转。 jetbrains全家桶(如Pycharm、Int…...

【技术干货】工业级BLE5.2蓝牙模块SKB378 使用教程,AT指令集
SKB378是一个高度集成的蓝牙5.2模组,可用来在2.4GHz ISM频段内做高速率、短距离无线通信。工业级标准,支持主从模式(1主对8从),支持串口透传,AT指令控制,且支持AoA蓝牙高精度室内定位,模组内部集成32位ARM …...
零基础深度学习——学习笔记1 (逻辑回归)
前言 因为各种各样的原因要开始学习深度学习了,跟着吴恩达老师的深度学习视频,自己总结一些知识点,以及学习中遇到的一些问题,以便记录学习轨迹以及以后复习使用,为了便于自己理解,我会将一些知识点用以个…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
