C++--动态规划路径问题
1.不同路径 力扣
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右示例 2:
输入:obstacleGrid = [[0,1],[0,0]]
输出:1来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/unique-paths-ii
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int r=obstacleGrid.size();int l=obstacleGrid[0].size();vector<vector<int>> dp(r+1,vector<int>(l+1));dp[1][0]=1;for(int i=1;i<=r;i++){for(int j=1;j<=l;j++){if(obstacleGrid[i-1][j-1]==0){dp[i][j]=dp[i][j-1]+dp[i-1][j]; }else {dp[i][j]=0;}}}return dp[r][l];}
};2.不同路径 力扣
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下示例 3:
输入:m = 7, n = 3
输出:28示例 4:
输入:m = 3, n = 3
输出:6来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/unique-paths
class Solution {
public:int uniquePaths(int m, int n) {//以某一处为结尾,创建dp表vector<vector<int>> dp(m+1,vector<int>(n+1));//初始化dp表//dp[0][1]=1;dp[1][0]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1];//递推公式}}return dp[m][n];}
};3.礼物的最大价值 力扣
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
示例 1:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/li-wu-de-zui-da-jie-zhi-lcof
class Solution {
public:int maxValue(vector<vector<int>>& grid) {int m=grid.size();int n=grid[0].size();vector<vector<int>> arr(m+1,vector<int>(n+1));//初始化,求最大,所以初始化最小,vector默认初始//化为0for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){arr[i][j]=max(arr[i-1][j],arr[i][j-1])+grid[i-1][j-1];//递推公式}}return arr[m][n];}
};4.下降路径最小和 力扣
给你一个 n x n 的 方形 整数数组 matrix ,请你找出并返回通过 matrix 的下降路径 的 最小和 。
下降路径 可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。具体来说,位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。
示例 1:
输入:matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出:13
解释:如图所示,为和最小的两条下降路径示例 2:
输入:matrix = [[-19,57],[-40,-5]]
输出:-59
解释:如图所示,为和最小的下降路径来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/minimum-falling-path-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
5.最小路径和 力扣
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/minimum-path-sum
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int n=matrix.size();vector<vector<int>> dp(n+1,vector<int>(n+2,INT_MAX));//创建dp表,并初始化为最大值for(int i=0;i<n+2;i++) dp[0][i]=0;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dp[i][j]=min(dp[i-1][j-1],min(dp[i-1][j],dp[i-1][j+1]))+matrix[i-1][j-1];//递推公式}}int ret=INT_MAX;for(int i=0;i<=n;i++)ret=min(ret,dp[n][i]);//找最小return ret;}
};class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int r=grid.size();int l=grid[0].size();vector<vector<int>> dp(r+1,vector<int>(l+1,INT_MAX));//创建dp表,并初始化,找最小,初始化为最大dp[0][1]=dp[1][0]=0;//由于有两种走法,所以要求drid[0][0]的上方和左边的为最小数0for(int i=1;i<=r;i++){for(int j=1;j<=l;j++){dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];//地推公式}}return dp[r][l];//返回值}
};6.地下城游戏 力扣
恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
示例 1:
输入:dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出:7
解释:如果骑士遵循最佳路径:右 -> 右 -> 下 -> 下 ,则骑士的初始健康点数至少为 7 。示例 2:
输入:dungeon = [[0]]
输出:1来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/dungeon-game
class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {int r=dungeon.size();int l=dungeon[0].size();vector<vector<int>> dp(r+1,vector<int>(l+1,INT_MAX));//创建dp表+初始化dp[r][l - 1] = dp[r - 1][l] = 1;for(int i=r-1;i>=0;i--){for(int j=l-1;j>=0;j--){dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j];//填表+递推公式if(dp[i][j]<=0)dp[i][j]=1;}}return dp[0][0];//返回值}
}相关文章:

C++--动态规划路径问题
1.不同路径 力扣 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。 现在考虑网格中有障碍物。那么从…...
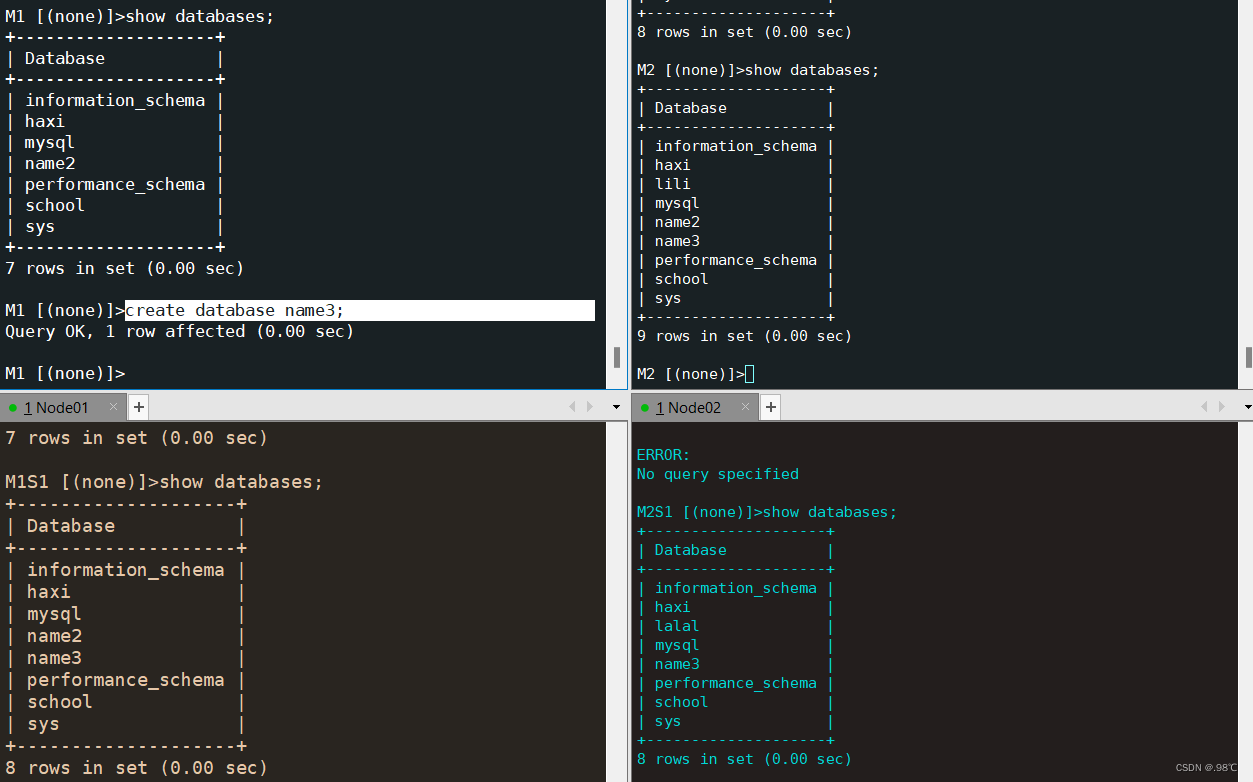
从实践彻底掌握MySQL的主从复制
目录 一、本次所用结构如图---一主多从级联: 二、IP。 三、配置M1: 四、从库M1S1: 五、从库M2配置: 六、 从库M2S1: 一、本次所用结构如图--- 一主多从级联: 二、IP。这里M1S1和M1S2一样的࿰…...

机器学习深度学习——线性回归的基本元素
回归用来表示输入输出之间的关系。 用实际例子来解释一下线性回归:根据房屋的面积、房龄来估算房屋价格。为了实现这个预测放假的模型,需要收集一个真实的数据集,该数据集包括了房屋的销售价格、面积和房龄。 在机器学习中,这个数…...
K8S初级入门系列之八-网络
一、前言 本章节我们将了解K8S的相关网络概念,包括K8S的网络通讯原理,以及Service以及相关的概念,包括Endpoint,EndpointSlice,Headless service,Ingress等。 二、网络通讯原理和实现 同一K8S集群&…...

分段@Transactional 坑及失效问题
Transactional 背景:在某些情况下,我们需要分段transaction,在最外面没有transaction,里面分成几个transaction,保证分段是成功的。 问题代码: Service public Order getOrder1(String id) {Optional<Or…...
25、matlab里面的10中优化方法介绍——Opt_Golden法(matlab程序)
1.简述 基本思想 黄金分割法也称为 0.618 法,其基本思想是通过取试探点和进行函数值比较,使包含极小点的搜索区间不断缩短以逼近极小值点。适用于确定区间上的任何单谷函数求极小值的问题。 公式推导 设有定义在[ a , b ] [a,b][a,b]上的单谷函数 φ ( …...

点云拟合球体
前言:在很多情况下,需要根据点云来拟合球体,本博文主要介绍各种方法的拟合情况及优缺点,希望对各位小伙伴有所帮助! 目录 1. vtkFitImplicitFunction进行球拟合 2. 四点求解球 1. vtkFitImplicitFunction进行球拟合 …...
算法的增程式EV能量管理策略研究(MATLAB编程))
基于动态规划(DP)算法的增程式EV能量管理策略研究(MATLAB编程)
文章目录 算法代码仿真结果结果分析算法代码 clc; clear; close all; load CWTVC.mat N=length(T_z); %N=200;load minFuelConsup.txt minFuel_Pe=minFuelConsup(:...

前端知识点视频补充
使用工具: Vscode使用: 需要下载插件:open in browser。这个插件可以快速打开浏览器。 选择文件夹有两种方式:选择打开文件、拖拽方式(这种最方便) 快捷键:快速生成Htm结构文件:…...

python多线程—终止子线程
总体思路 1、获取需要终止的子线程id 2、根据子线程id,终止子线程。 过程 获取子线程id: import threading Thread_id threading.get_ident() # 获取子线程的id值线程终止函数 def async_raise(Thread_id, exctype):"""raises th…...

#P1012. [NOIP2015提高组] 神奇的幻方
题目描述 幻方是一种很神奇的 N \times NNN 矩阵:它由数字 1,2,3, \ldots ,N \times N1,2,3,…,NN 构成,且每行、每列及两条对角线上的数字之和都相同。 当 NN 为奇数时,我们可以通过以下方法构建一个幻方: 首先将 11 写在第一行…...
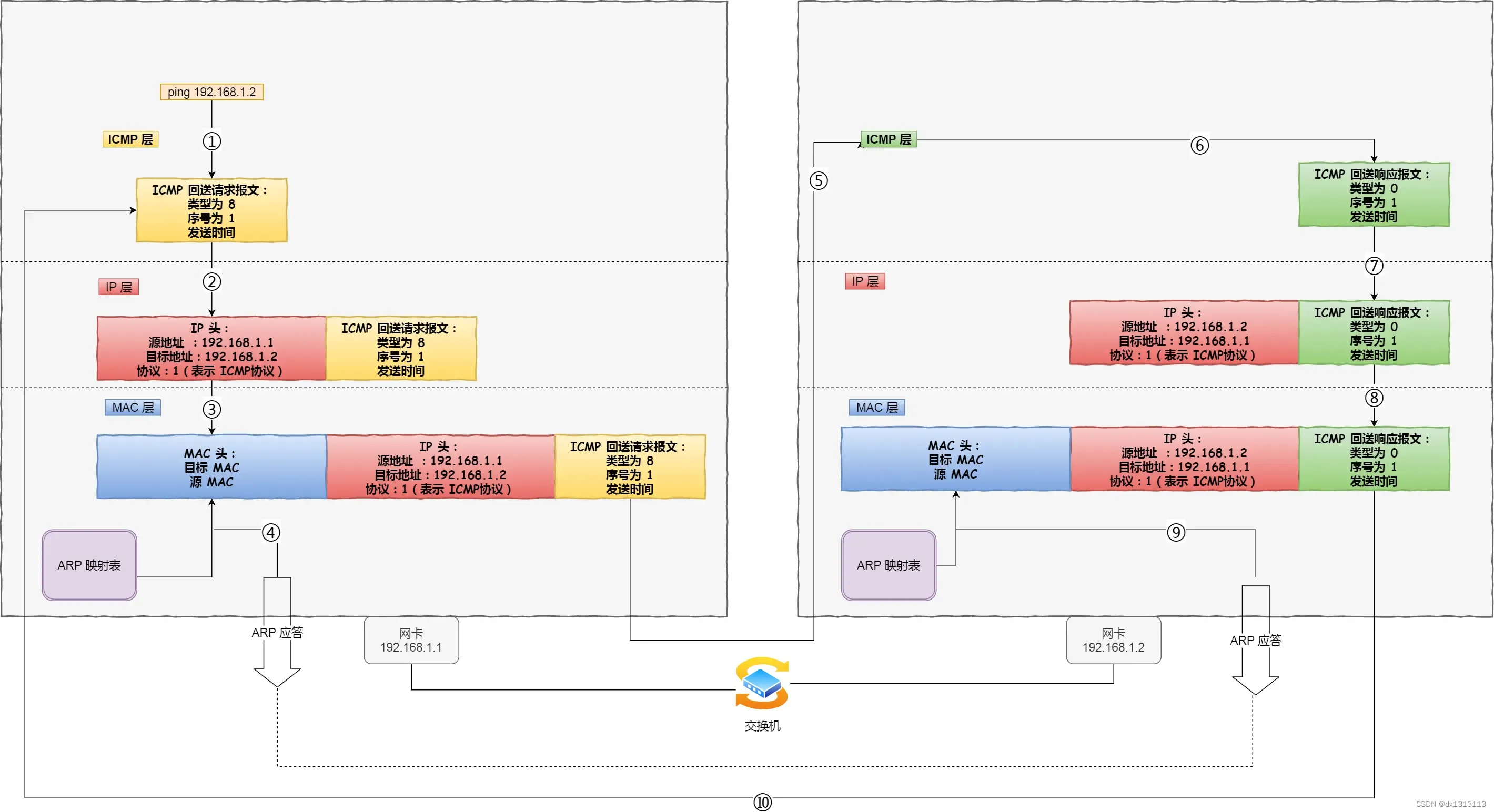
(学习笔记-IP)Ping的工作原理
Ping是基于ICMP协议工作的,ICMP报文封装在IP包里面,它工作在网络层,是IP协议的助手。 ICMP包头的类型字段,大致可分为两大类: 一类是用于诊断的查询消息,也就是查询报文类型一类是通知出错原因的错误消息&…...

php 进程间通信:管道、uds
1、管道 1.1、管道概念 管道是单向的、先进先出的,它把进程的输出和另一个进程的输入连接在一起。一个进程往管道写入数据,另一个进程从管道读取数据。数据被从管道中读取出来之后,将被删除,其他进程无法在读取到相应的数据。管…...

Stable Diffusion如何生成高质量的图-prompt写法介绍
文章目录 Stable Diffusion使用尝试下效果prompt的编写技巧prompt 和 negative promptPrompt格式Prompt规则细节优化Guidance Scale 总结 Stable Diffusion Stable Diffusion是一个开源的图像生成AI系统,由Anthropic公司开发。它基于 Transformer模型架构,可以通过文字描述生成…...

MySQL 高级SQL语句(一)
目录 一、高级SQL语句(进阶查询) 1.1 select 1.2 distinct 1.3 where 1.4 and 和 or 1.5 in 1.6 between 1.7 通配符 1.8 like 1.9 order by 一、高级SQL语句(进阶查询) 先准备2个表 一个location表: use m…...

SkyWalking链路追踪-技术文档首页
SkyWalking 文档中文版(社区提供) (skyapm.github.io)https://skyapm.github.io/document-cn-translation-of-skywalking/ SkyWalking-基本概念 SkyWalking链路追踪是一个用于分布式系统的性能监控工具,它帮助开发人员了解系统中各组件之间…...
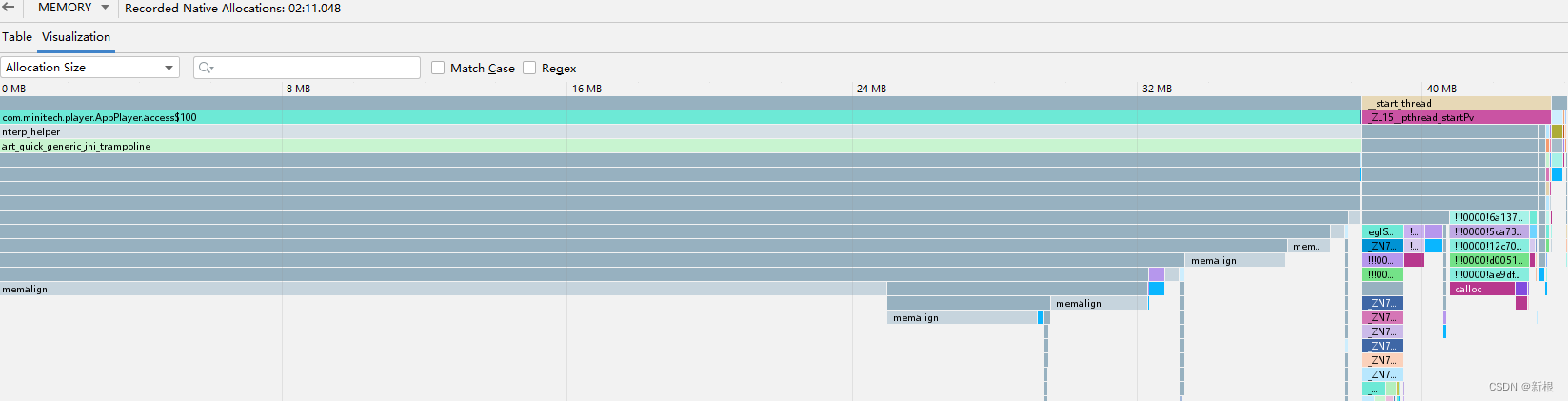
AndroidStudio Memory profiler(内存分析器)
1.Record Java/Kotlin allocations 查看java 层中对象的调用栈和短时间内创建对象的次数。可用于内存抖动快速分析,可用快速查找到该对象的调用栈(等同于mat) 从上图可见,短时间内创建了23个char[] 数组,其中最大的char[] 占用20k, 查看cll stack 调用…...

【C++模板进阶】
目录 一、模板使用时的一个小注意点二、非类型模板参数三、类模板的特化3.1函数模板的特化3.2类模板的特化3.2.1全特化3.2.2偏特化 四、模板的分离编译4.1模板不支持分离编译4.2模板分离编译报错的分析4.2解决方案 五、模板的总结 一、模板使用时的一个小注意点 在使用模板时&…...
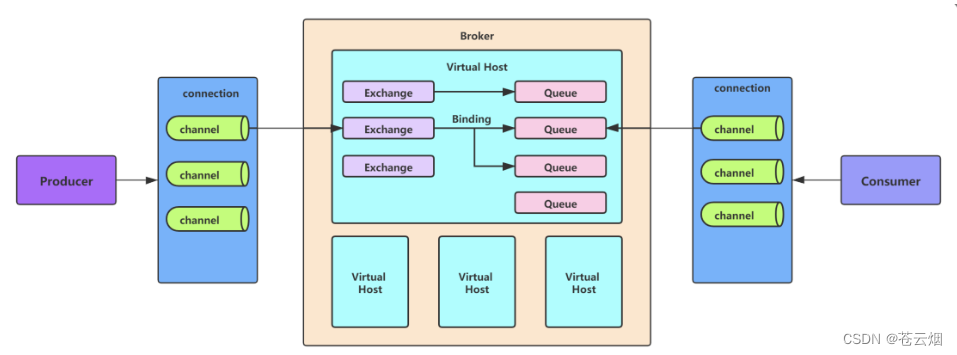
(一)RabbitMQ概念-优势、劣势、应用场景 、AMQP、工作原理
Lison <dreamlison163.com>, v1.0.0, 2023.06.22 RabbitMQ概念-优势、劣势、应用场景 、AMQP、工作原理 文章目录 RabbitMQ概念-优势、劣势、应用场景 、AMQP、工作原理RabbitMQ概念RabbitMQ的优势RabbitMQ劣势RabbitMQ应用的场景RabbitMQ_AMQPRabbitMQ工作原理 RabbitM…...
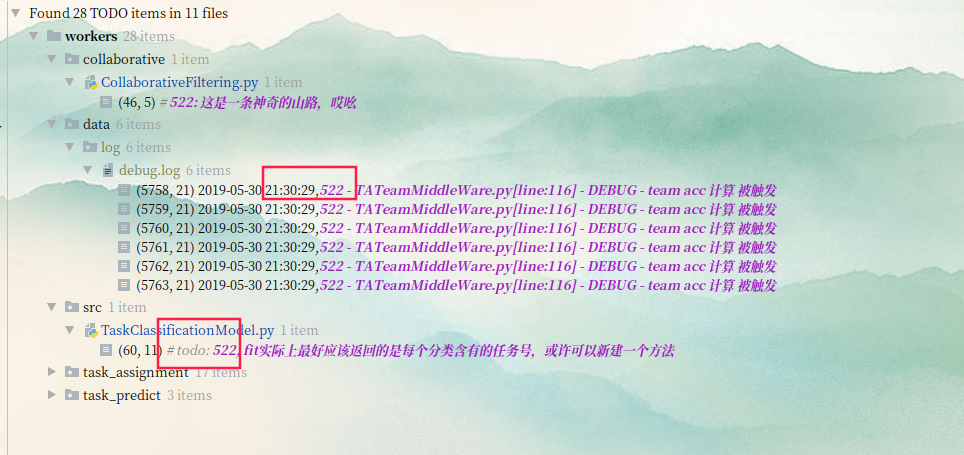
JetBrains全家桶:如何自定义实现类TODO注释?
文章目录 效果图具体方法参考文献 效果图 TODO注释大家应该都用过,在注释开头打上TODO的话,软件下方的TODO选项卡里就可以自动筛选出你打了TODO的注释,你可以点击里面对应的注释来实现快速跳转。 jetbrains全家桶(如Pycharm、Int…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
