【算法基础:搜索与图论】3.6 二分图(染色法判定二分图匈牙利算法)
文章目录
- 二分图介绍
- 染色法判定二分图
- 例题:860. 染色法判定二分图
- 匈牙利匹配
- 二分图最大匹配
- 匈牙利匹配算法思想
- 例题:861. 二分图的最大匹配
二分图介绍
https://oi-wiki.org/graph/bi-graph/
二分图是图论中的一个概念,它的所有节点可以被分为两个独立的集合,每个边的两个端点分别来自这两个不同的集合。
换句话说,二分图中不存在连接同一集合内两个节点的边。


染色法判定二分图
如何判断一个图是二分图?
当且仅当图中不含奇数环。(奇数环指的是环中边的个数是奇数)(因为每一条边都是从一个集合走到另一个集合,只有走偶数次才有可能回到同一个集合。)
染色:相邻的节点的颜色不一样。
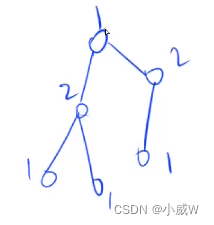
因为没有奇数环,所以染色过程是一定不会发生矛盾的。
时间复杂度是 O ( n + m ) O(n + m) O(n+m) , n 表示点数,m 表示边数。
例题:860. 染色法判定二分图
https://www.acwing.com/activity/content/problem/content/926/
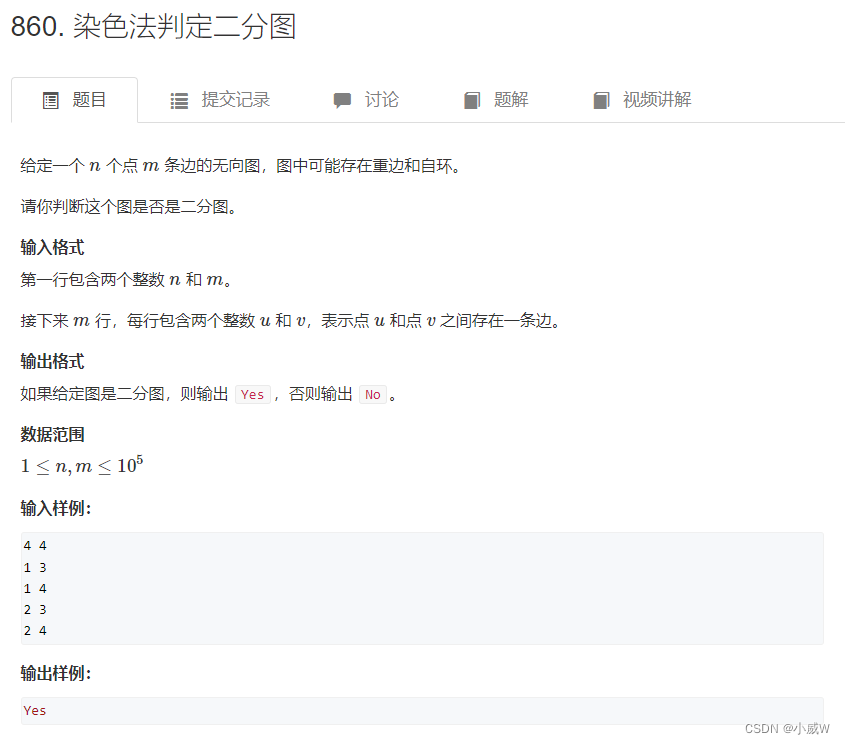
使用 dfs 对图中各个节点染色,染色过程中不发生冲突即为二分图。
import java.util.*;public class Main {static final int N = 100005;static List<Integer>[] g = new ArrayList[N];static int[] color = new int[N];public static void main(String[] args){Scanner sc = new Scanner(System.in);int n = sc.nextInt(), m = sc.nextInt();// 建图Arrays.setAll(g, e -> new ArrayList<Integer>());for (int i = 0; i < m; ++i) {int u = sc.nextInt(), v = sc.nextInt();g[u].add(v);g[v].add(u);}// 图可能由多个非连通的子图构成。因此,应该对每一个尚未访问过的点都进行一次深度优先搜索。boolean f = true;for (int i = 1; i <= n; ++i) {if (color[i] == 0 && !dfs(i, 1)) {f = false;break;}}System.out.println(f? "Yes": "No");}static boolean dfs(int x, int c) {boolean res = true;color[x] = c;for (int y: g[x]) {if (color[y] == 0) res &= dfs(y, 3 - c);else if (color[y] == color[x]) return false;}return res;}
}匈牙利匹配
二分图最大匹配
**二分图最大匹配**:
翻译成人话就是——
给定一个二分图 G,即分左右两部分,各部分之间的点没有边连接,要求选出一些边,使得这些边没有公共顶点,且边的数量最大。
匈牙利匹配算法思想
两个集合的点数分别是 n1 , n2。
枚举 n1 , 尝试 i 是否可以找到一个 j 完成匹配,匹配成功就 ++cnt。
所以重点是 find(i) 方法:
对每个 i ,枚举 i 相邻的所有 j —— 如果 j 没有被匹配就直接返回 true;如果 j 被匹配了,就尝试现在和 j 匹配的另一个 i 能不能换一个 j,能换就换一个然后返回 true;否则返回 false。
时间复杂度是 O ( n ∗ m ) O(n * m) O(n∗m),n 表示点数,m 表示边数。
例题:861. 二分图的最大匹配
https://www.acwing.com/activity/content/problem/content/927/

重点是理解数组 match 和 st 的含义,以及方法 find(x) 的写法和使用。
import java.util.*;public class Main {static final int N = 505;static int[][] g = new int[N][N];static int[] match = new int[N]; // match记录集合2中各个点匹配的集合1的点是哪个static boolean[] st = new boolean[N]; // st表示集合2中的点有没有被匹配static int n1, n2;public static void main(String[] args){Scanner sc = new Scanner(System.in);n1 = sc.nextInt();n2 = sc.nextInt();int m = sc.nextInt();// 建图for (int i = 0; i < m; ++i) {int u = sc.nextInt(), v = sc.nextInt();g[u][v] = 1; // 左边的 u 和 右边的 v 之间有一条边}int cnt = 0;for (int i = 1; i <= n1; ++i) {Arrays.fill(st, false); // 重置stif (find(i)) ++cnt;}System.out.println(cnt);}static boolean find(int x) {for (int j = 1; j <= n2; ++j) {if (!st[j] && g[x][j] == 1) {st[j] = true;// 如果 j 还没有匹配或者当前使用 j 的 x 可以让出去if (match[j] == 0 || find(match[j])) {match[j] = x;return true;}}}return false;}
}相关文章:

【算法基础:搜索与图论】3.6 二分图(染色法判定二分图匈牙利算法)
文章目录 二分图介绍染色法判定二分图例题:860. 染色法判定二分图 匈牙利匹配二分图最大匹配匈牙利匹配算法思想例题:861. 二分图的最大匹配 二分图介绍 https://oi-wiki.org/graph/bi-graph/ 二分图是图论中的一个概念,它的所有节点可以被…...

SpringMVC 怎么和 AJAX 相互调用的
通过 Jackson 框架就可以把 Java 里面的对象直接转化成 Js 可以识别的 Json 对象。 步骤如下 : a、加入 Jackson.jar b、在配置文件中配置 json 的映射 c、在接受 Ajax 方法里面可以直接返回 Object,List 等,但方法前面要加上ResponseBody 详细步骤: …...
UCDOS和WPS推动计算机领域的汉字化发展,中文编程该谁力扛大旗?
你还记得UCDOS吗? 从DOS时代过来的人,还知道UCDOS的,现在可能已经是中年人了! 当时,鲍岳桥的UCDOS可以称得上是中国的国产操作系统。 在Windows还没来得及进入中国市场时,UCDOS可以说是走向了巅峰时刻&a…...

golang+layui提升界面美化度--[推荐]
一、背景 golanglayui提升界面美化度--[推荐]; golang后端写的页面很难看,如何好看点呢,那就是layui https://layui.dev/ 也是一个简单上手容易使用的框架,类似jquery,对于后端开发来说满足使用需求 二、使用注意点…...

42. 接雨水
题目介绍 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3…...

Python学习阶段路线和内容
Python学习阶段路线和内容 这是我的看法和认识,供参考。 Python学习路线主要分为三个阶段:入门阶段、提高阶段和深入阶段。 入门阶段 入门阶段需要学习Python的基本语法,掌握变量和数据类型、条件语句和循环语句、函数和模块等内容。并通过…...
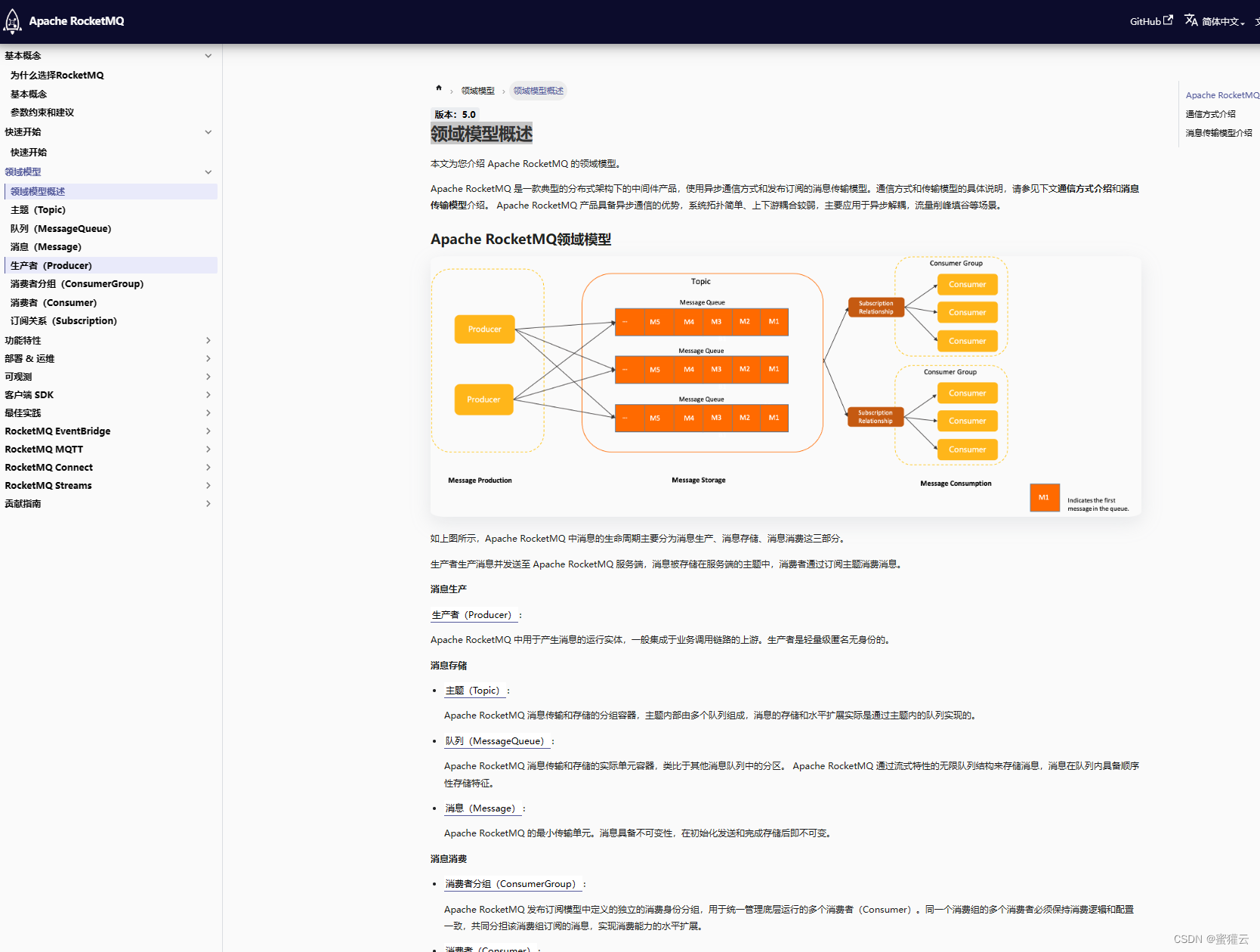
RocketMQ教程-安装和配置
Linux系统安装配置 64位操作系统,推荐 Linux/Unix/macOS 64位 JDK 1.8 Maven3.0 yum 安装jdk8 yum 安装maven 1.下载安装Apache RocketMQ RocketMQ 的安装包分为两种,二进制包和源码包。 点击这里 下载 Apache RocketMQ 5.1.3的源码包。你也可以从这…...

【LeetCode】55.跳跃游戏
题目 给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标。 示例 1: 输入:nums [2,3,1,1,4] 输出:true 解释:可以…...

Docker学习路线12:开发者体验
到目前为止,我们只讨论了使用Docker来部署应用程序。然而,Docker也是一个极好的用于开发应用程序的工具。可以采用一些不同的建议来改善开发体验。 在应用程序中使用docker-compose以方便开发。使用绑定挂载将本地代码挂载到容器文件系统中,…...

后端服务迁移方案及过程记录
阶段时序动作双写数据对比1新rdb集群上线双写数据对比2新服务上线,无流量双写数据对比2后端自己发起的流程比如job,新服务上线一份新的,独立运行双写数据对比2消费二方mq,新服务使用新的消费组消费原有消息双写数据对比3新旧服务比…...

StAX解析
StAX解析 StAX解析介绍 StAX解析与SAX解析类似,也是基于事件驱动的,不同之处在于StAX采用的是拉模式,应用程序通过调用解析器推进解析的进程,可以调用next()方法来获取下一个解析事件(开始文档,结束文档,开…...

[MCU]AUTOSAR COM STACK - CAN协议栈
各层PDU PDU:Protocal Data Unit,协议数据单元,由SDU和PCI组成; I-PDU:Interaction Layer PDU,数据交互层PDU;N-PDU:NetWork Layer PDU,网络层PDU,通常用的…...

React:从 npx开始
使用 npm 来创建第一个 recat 文件( react-demo 是文件名,可以自定义) npx create-react-app react-demo npx是 npm v5.2 版本新添加的命令,用来简化 npm 中工具包的使用 原始: 全局安装npm i -g create-react-app 2 …...
力扣热门100题之接雨水【困难】
题目描述 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3…...

Stable-Diffusion-Webui部署SDXL0.9报错参数shape不匹配解决
问题 已经在model/stable-diffusion文件夹下放进去了sdxl0.9的safetensor文件,但是在切换model的时候,会报错model的shape不一致。 解决方法 git pullupdate一些web-ui项目就可以,因为当前项目太老了,没有使用最新的版本。...

Springboot @Async 多线程获取返回值
Springboot Async 多线程获取返回值 需求背景 最近需要用到多线程, 自己维护线程池很麻烦, 正好看到Springboot集成线程池的例子, 这里自己做了个尝试和总结, 记录一下, 也分享给需要的朋友; 不考虑事务的情况下, 这个多线程实现比较简单, 主要有以下几点: 在启动类加上Enab…...

怎样接入chatGPT
官网链接: OpenAI platform...
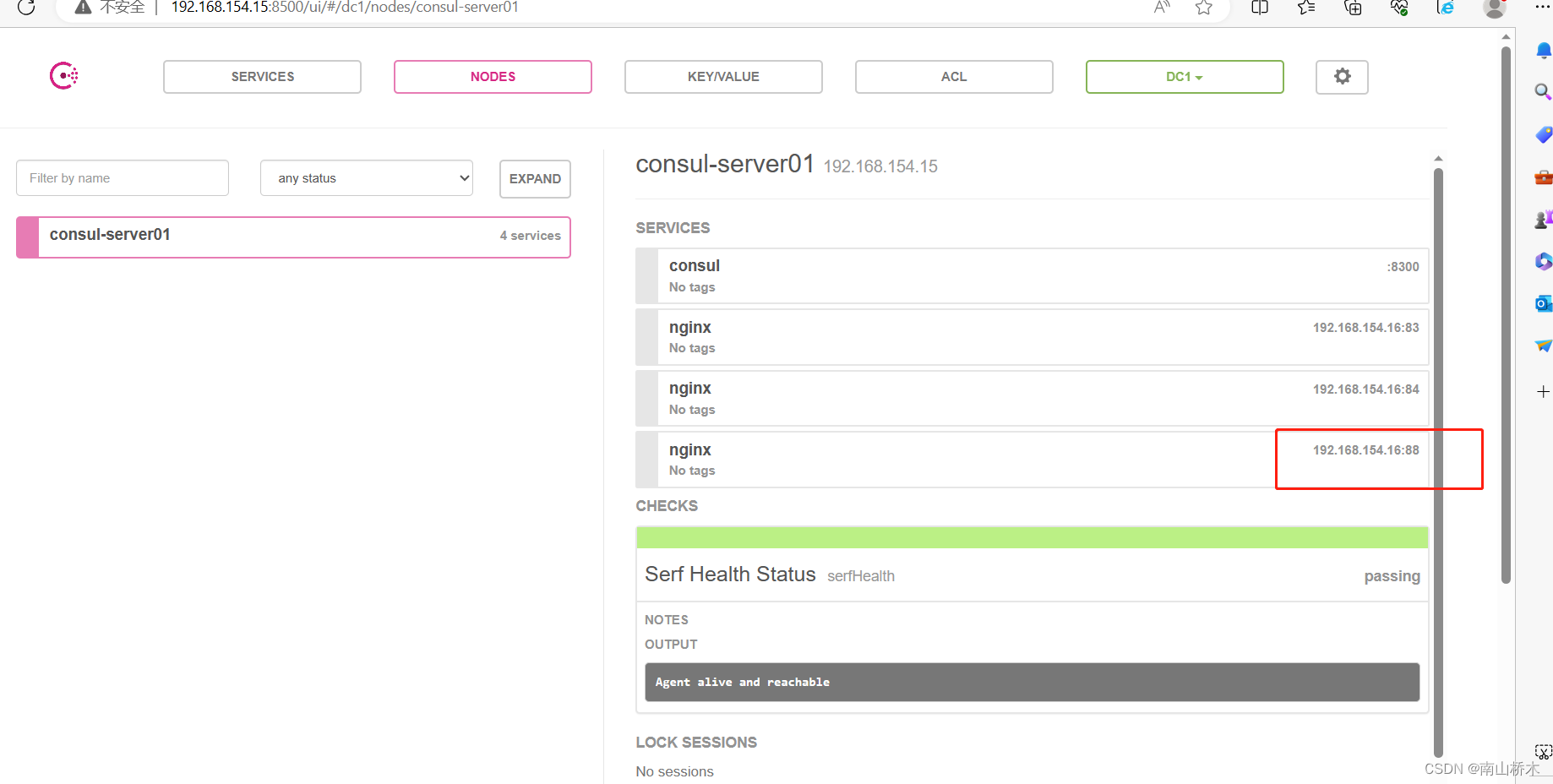
Docker consul容器服务更新与发现
Docker consul容器服务更新与发现 一、什么事服务注册与发现二、什么是consul三、consul部署1、consul服务器2、registrator服务器3、consul-template 一、什么事服务注册与发现 服务注册与发现是微服务架构中不可或缺的重要组件。起初服务都是单节点的,不保障高可…...

[算法很美打卡] 多维数组篇 (打卡第一天)
文章目录 顺时针打印二维数组0所在的行列清零 顺时针打印二维数组 package 每日算法学习打卡.算法打卡.七月份.七月二十六号;public class test1 {public static void main(String[] args) {int[][] matrix {{1,2},{5,6},{9,10},{13,14},};print(matrix);}static void print(i…...
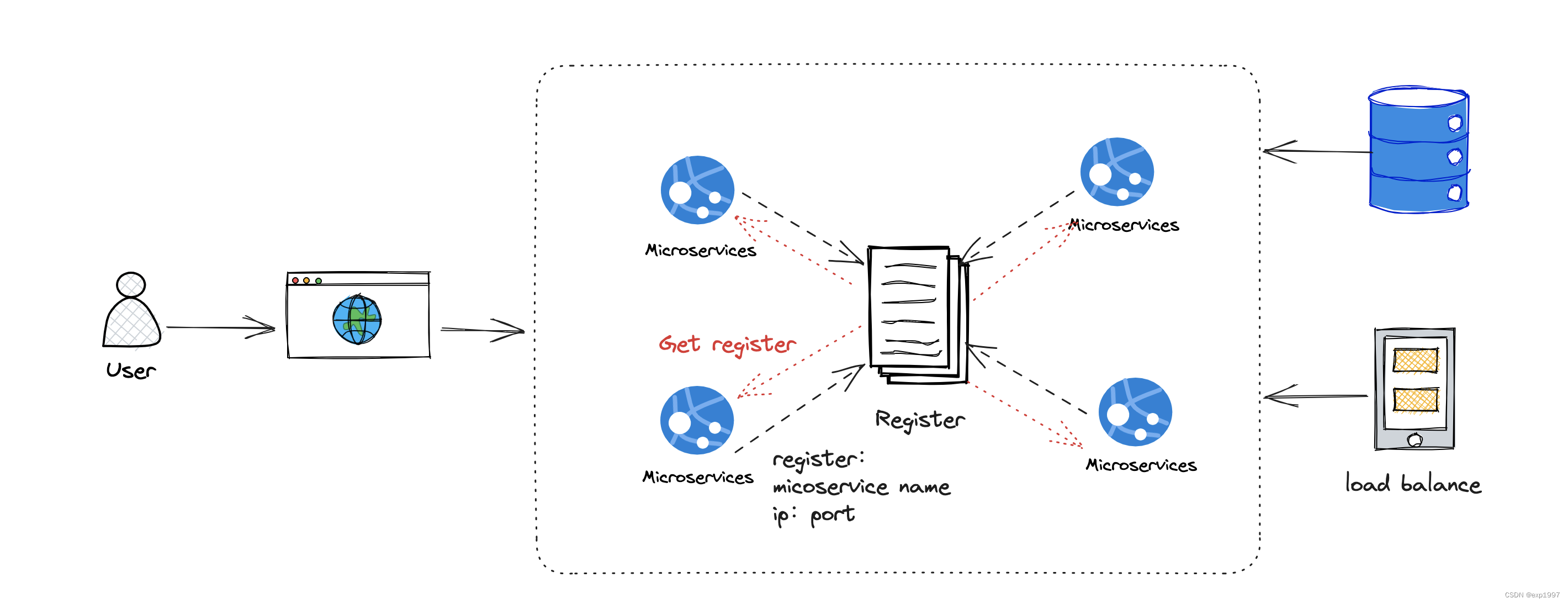
微服务系列(1)-who i am?
微服务系列(1)-我是谁 应用架构的演化 简单来说系统架构可以分为以下几个阶段:复杂的臃肿的单体架构-SOA架构-微服务 单体架构及其所面临的问题 在互联网发展初期,用户数量少,流量小,硬件成本高。因此…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
