车道线检测|利用边缘检测的原理对车道线图片进行识别
前言
那么这里博主先安利一些干货满满的专栏了!
这两个都是博主在学习Linux操作系统过程中的记录,希望对大家的学习有帮助!
操作系统Operating Sys![]() https://blog.csdn.net/yu_cblog/category_12165502.html?spm=1001.2014.3001.5482
https://blog.csdn.net/yu_cblog/category_12165502.html?spm=1001.2014.3001.5482![]() https://blog.csdn.net/yu_cblog/category_11786077.html?spm=1001.2014.3001.5482这两个是博主学习数据结构的同时,手撕模拟STL标准模版库各种容器的专栏。
https://blog.csdn.net/yu_cblog/category_11786077.html?spm=1001.2014.3001.5482这两个是博主学习数据结构的同时,手撕模拟STL标准模版库各种容器的专栏。
STL源码剖析![]() https://blog.csdn.net/yu_cblog/category_11983210.html?spm=1001.2014.3001.5482手撕数据结构
https://blog.csdn.net/yu_cblog/category_11983210.html?spm=1001.2014.3001.5482手撕数据结构![]() https://blog.csdn.net/yu_cblog/category_11490888.html
https://blog.csdn.net/yu_cblog/category_11490888.html
一、摘要
本次实验,通过学习边缘检测的原理,使用Matlab编程语言,完成对输出给定图像的边缘检测图像和完成车道线识别。
二、实验内容及目的
输出给定图像的边缘检测图像和完成车道线识别。
三、实验相关原理描述
边缘检测是一种图像处理技术,用于在图像中检测出物体或场景的边缘或轮廓。其原理是通过分析图像中的亮度或颜色变化来识别边缘位置。常用的边缘检测方法包括Sobel、Prewitt、Canny等。
下面是本次实验主要流程:
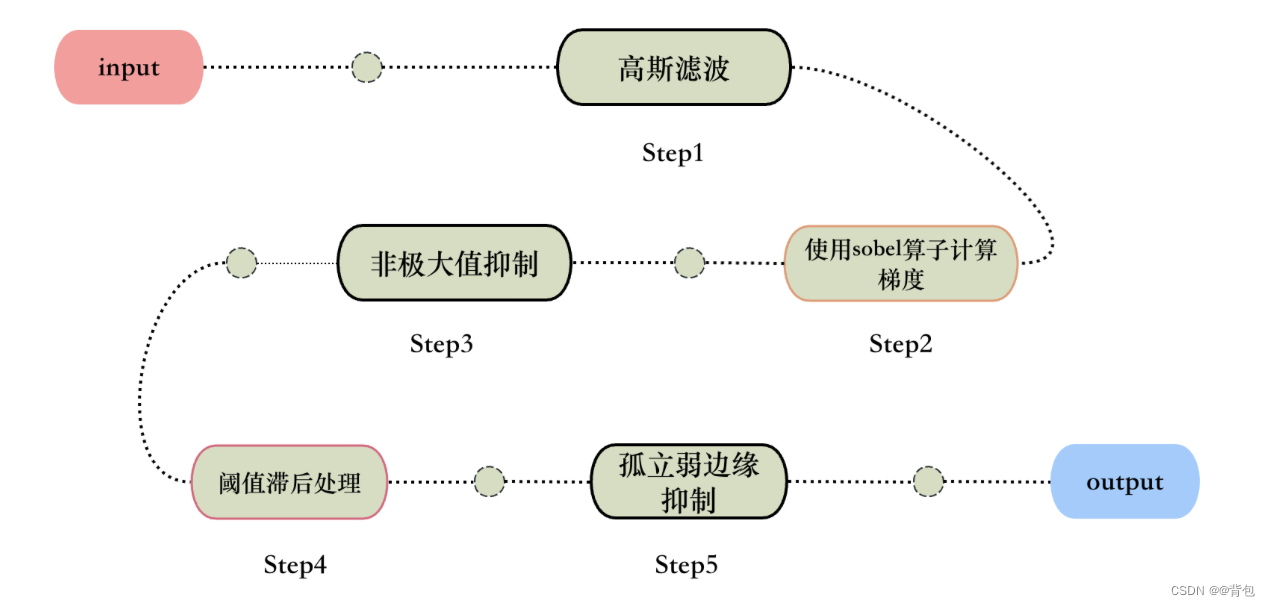
主要步骤原理
高斯滤波:
高斯滤波是一种常用的图像处理技术,用于平滑图像、去除噪声和边缘检测等应用。它基于高斯函数(也称为正态分布函数)的概念,通过对图像中的像素进行加权平均来实现平滑效果。
高斯滤波的公式如下:
其中,G(x,y) 表示高斯滤波器在坐标(x,y) 处的权重值,σ 表示高斯函数的标准差,控制了滤波器的模糊程度。标准差越大,滤波器的模糊程度越高。
高斯滤波的原理是利用高斯函数的权重值对图像中的像素进行加权平均。滤波器的中心像素权重最大,越远离中心像素的像素权重越小。通过对邻近像素进行加权平均,可以使图像中的噪声平均化,并且能够保留图像的整体结构和边缘特征。
Sobel算子计算梯度:
水平方向的 Sobel 算子:
垂直方向的Sobel算子:
这些模板是 3x3 的矩阵,分别对应着水平和垂直方向上的微分操作。通过将这些模板与图像进行卷积操作,可以得到图像在水平和垂直方向上的梯度值。
非极大值抑制:
非极大值抑制可以用来寻找像素点局部最大值,将非极大值所对应的灰度值置0,极大值点置1,这样可以剔除一大部分非边缘的像素点,从而得到一副二值图像,边缘理想状态下都为单像素边缘。
四、实验过程和结果
% 读取图片
img = imread('图像路径');
imshow(img);
% 将图像转换为灰度
gray_img = rgb2gray(img);
% 高斯滤波
sigma = 2; % 高斯滤波器的标准差
gaussian_filtered_img = imgaussfilt(gray_img, sigma);
% 使用Sobel算子进行梯度计算
sobel_filtered_img = double(edge(gaussian_filtered_img, 'sobel'));
% 显示原始图像和处理后的图像
imshow(img); title('原始图像');
imshow(sobel_filtered_img); title('梯度计算后的图像');
% 定义梯度方向
directions = [-pi/2, -pi/4, 0, pi/4, pi/2, 3*pi/4, pi, -3*pi/4];% 对每个像素,找到沿着梯度方向的两个相邻像素,计算它们的插值
nms_img = zeros(size(sobel_filtered_img));
for i=2:size(sobel_filtered_img,1)-1for j=2:size(sobel_filtered_img,2)-1% 找到最近的两个方向[~, index] = min(abs(directions - atan2d(-sobel_filtered_img(i,j), sobel_filtered_img(i,j+1))));if index == 1 || index == 5left = sobel_filtered_img(i-1,j-1);right = sobel_filtered_img(i+1,j+1);elseif index == 2 || index == 6left = sobel_filtered_img(i-1,j+1);right = sobel_filtered_img(i+1,j-1);elseif index == 3 || index == 7left = sobel_filtered_img(i,j-1);right = sobel_filtered_img(i,j+1);elseif index == 4 || index == 8left = sobel_filtered_img(i+1,j-1);right = sobel_filtered_img(i-1,j+1);end% 如果像素值是局部最大值,则保留if sobel_filtered_img(i,j) >= left && sobel_filtered_img(i,j) >= rightnms_img(i,j) = sobel_filtered_img(i,j);endend
end% 显示非极大值抑制后的图像
figure; imshow(nms_img); title('非极大值抑制后的图像');
% 阈值滞后处理
low_threshold = 0.05;
high_threshold = 0.2;
edge_map = zeros(size(nms_img));
edge_map(nms_img > high_threshold) = 1;
for i=2:size(nms_img,1)-1for j=2:size(nms_img,2)-1if (nms_img(i,j) > low_threshold) && (edge_map(i,j) == 0)if (edge_map(i-1,j-1) == 1) || (edge_map(i-1,j) == 1) || (edge_map(i-1,j+1) == 1) || (edge_map(i,j-1) == 1) || (edge_map(i,j+1) == 1) || (edge_map(i+1,j-1) == 1) || (edge_map(i+1,j) == 1) || (edge_map(i+1,j+1) == 1)edge_map(i,j) = 1;endendend
end
imshow(edge_map);% 孤立弱边缘抑制
isolated_threshold = 1;
for i=2:size(edge_map,1)-1for j=2:size(edge_map,2)-1if (edge_map(i,j) == 1) && (sum(sum(edge_map(i-1:i+1,j-1:j+1))) <= isolated_threshold)edge_map(i,j) = 0;endend
end
imshow(edge_map);
% 车道线检测
% [m,n] = size(edge_map)
% x = [1600,0,0,1600];
% y = [1000,0,0,1000];
% mask = poly2mask(x,y,m,n);
% new_img = mask.*edge_map;
% imshow(new_img);new_img = edge_map;
lines = HoughStraightRecognize(new_img);hold on;
imshow(img);
for k = 1:length(lines)
% k = 7;
xy = [lines(k).point1; lines(k).point2];
plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');
plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');
endfunction lines = HoughStraightRecognize(BW)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%该函数为霍夫变换识别直线的函数
%input:图像(可以是二值图,也可以是灰度图)
%output:直线的struct结构,其结构组成为线段的两个端点
%以及在极坐标系下的坐标【rho,theta】
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%[H,T,R] = hough(BW);% imshow(H,[],'XData',T,'YData',R,...% 'InitialMagnification','fit');% xlabel('\theta'), ylabel('\rho');% axis on, axis normal, hold on;P = houghpeaks(H,5,'threshold',ceil(0.3*max(H(:))));%x = T(P(:,2)); y = R(P(:,1));%plot(x,y,'s','color','white');lines = houghlines(BW,T,R,P,'FillGap',5,'MinLength',7);%FillGap 两个线段之间的距离,小于该值会将两个线段合并%MinLength 最小线段长度
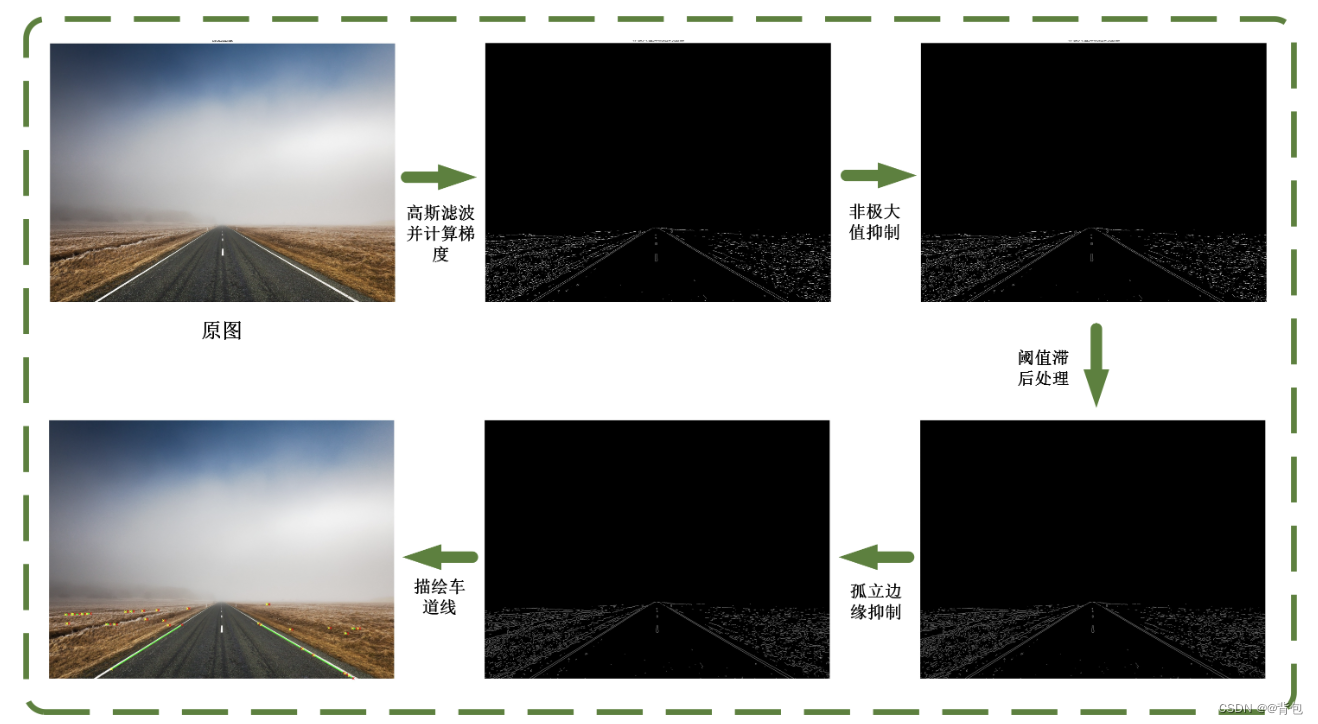
end实验过程所得到输出图像如下图所示:
相关文章:

车道线检测|利用边缘检测的原理对车道线图片进行识别
前言 那么这里博主先安利一些干货满满的专栏了! 这两个都是博主在学习Linux操作系统过程中的记录,希望对大家的学习有帮助! 操作系统Operating Syshttps://blog.csdn.net/yu_cblog/category_12165502.html?spm1001.2014.3001.5482Linux S…...

C++—static关键字详解
引言: C的static有两种用法:面向过程程序设计中的static和面向对象程序设计中的static。前者应用于普通变量和函数,不涉及类;后者主要说明static在类中的作用。 一.面向过程中的static 1.静态全局变量 静态全局变量有以下特点…...

CS144学习笔记(1):Internet and IP
1.网络应用 网络应用可以在世界范围内交换数据,例如你可以通过浏览器读取出版社服务器提供的文章。网络应用的基本模型:两台主机各自在本地运行一个程序,程序通过网络来通信。 最常用的通信模型使用双向可靠字节流,通信的两台主机…...
2 Linux基础篇-Linux入门
2Linux基础篇-Linux入门 文章目录 2Linux基础篇-Linux入门2.1 Linux介绍2.2 Linux和Unix的关系 学习视频来自于B站 【小白入门 通俗易懂】2021韩顺平 一周学会Linux。 2.1 Linux介绍 常见的操作系统有 Windows、MacOS、Android、ios、Linux、Unix等。而其中,Linux是…...

分享200+个关于AI的网站
分享200个关于AI的网站 欢迎大家访问:https://tools.haiyong.site/ai 快速导航 AI 应用AI 写作AI 编程AI 设计AI 作图AI 训练模型AI 影音编辑AI 效率助手 AI 应用 文心一言: https://yiyan.baidu.com/ 百度出品的人工智能语言模型 ChatGPT: https://chat.openai.c…...

静态 链接
1、空间与地址的分配 现在的链接器空间分配的策略基本上都采用 “相似段合并” 的方式。通过将所有相同类型的 section 合并到一起,例如将所有输入目标文件的 .text 合并(按顺序合并)到输出文件的 .text 节中;然后,链接…...
【C#性能】C# 语言中的数组迭代
一、说明 可迭代性,是数组等操作的根本;在C程序开发过程中,可迭代操作是非常普遍、非常广泛的,然而,对这种操作知道多少,又不知道多少,都将影响开发灵活性、开发的进度。因此,本文干…...
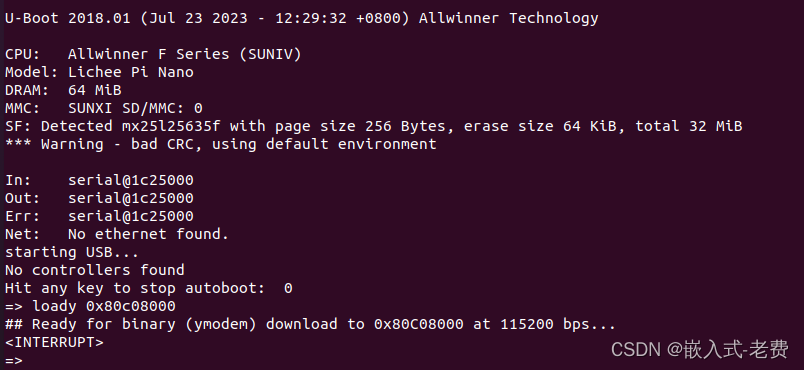
全志F1C200S嵌入式驱动开发(解决spi加载过慢的问题)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing @163.com】 之前的几个章节当中,我们陆续解决了spi-nor驱动的问题、uboot支持spi-nor的问题。按道理来说,下面要做的应该就是用uboot的loady命令把kernel、dtb、rootfs这些文件下载到ddr,然…...
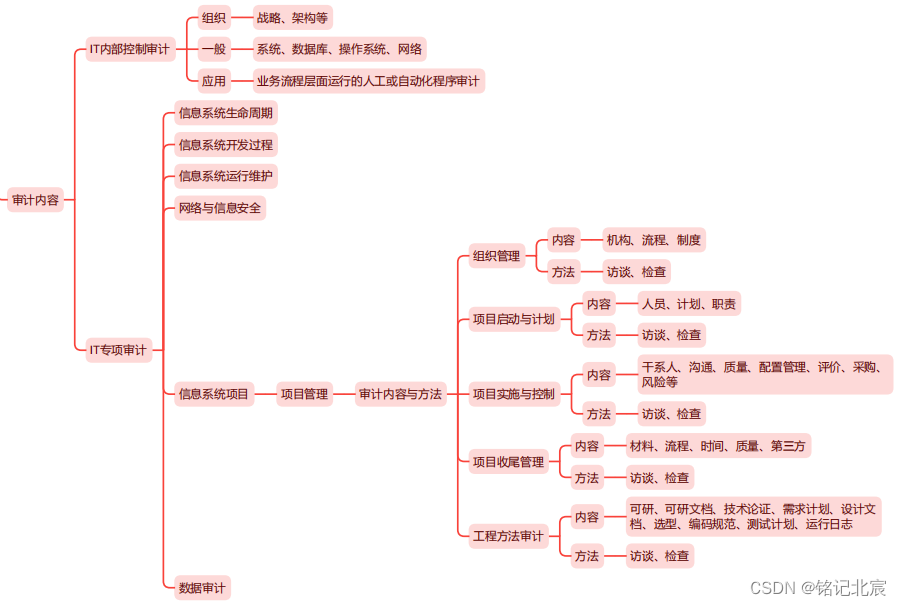
信息系统项目管理师(第四版)教材精读思维导图-第三章信息系统治理
请参阅我的另一篇文章,综合介绍软考高项: 信息系统项目管理师(软考高项)备考总结_计算机技术与软件专业技术_铭记北宸的博客-CSDN博客 目录 3.1 IT治理 3.2 IT审计 3.1 IT治理 3.2 IT审计...

区间预测 | MATLAB实现基于QRF随机森林分位数回归多变量时间序列区间预测模型
区间预测 | MATLAB实现基于QRF随机森林分位数回归多变量时间序列区间预测模型 目录 区间预测 | MATLAB实现基于QRF随机森林分位数回归多变量时间序列区间预测模型效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现基于QRF随机森林分位数回归多变量时间序列区间…...
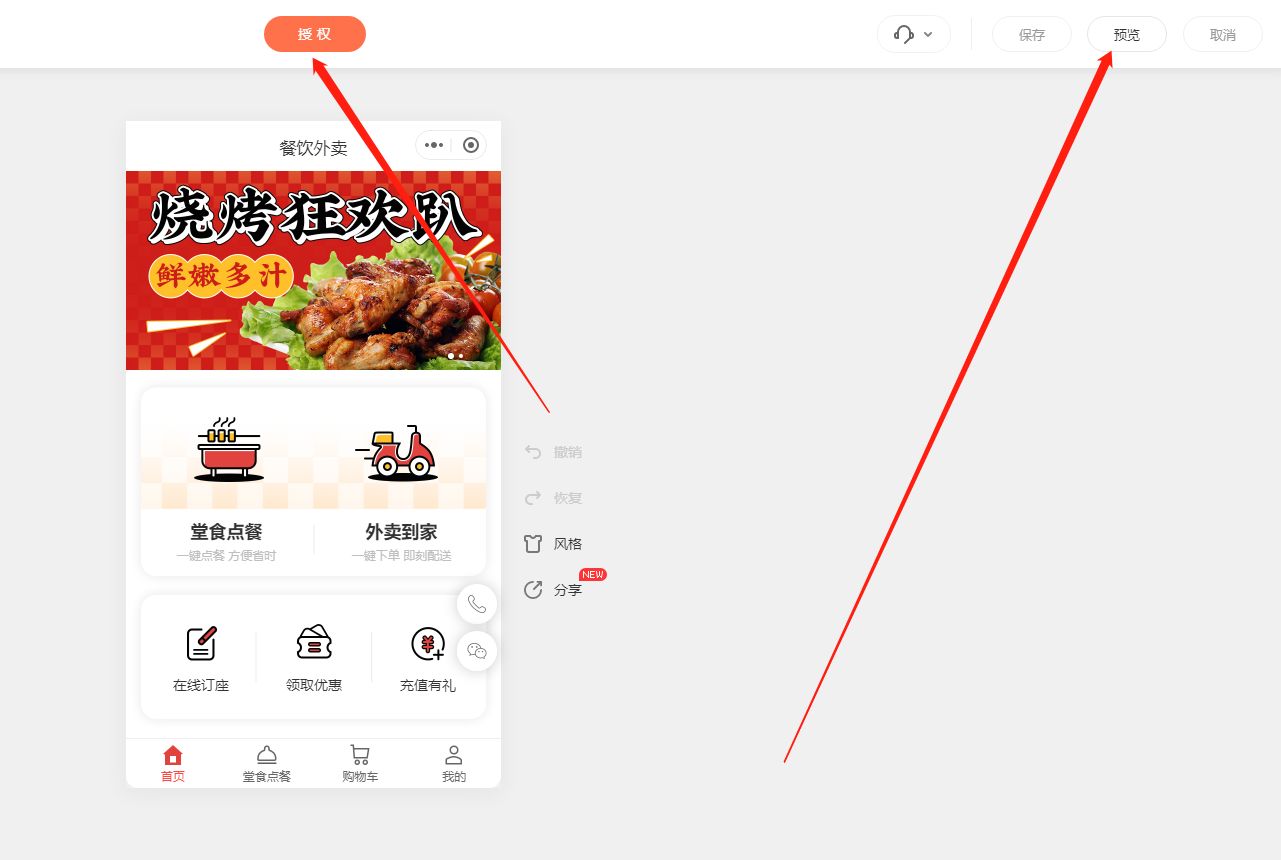
五步快速搭建个性化外卖小程序商城
随着人们生活节奏的加快,外卖行业蓬勃发展。为了满足用户的需求,许多企业开始使用小程序商城来提供外卖服务。那么,如何制作一个功能完善、用户友好的外卖小程序商城呢?下面就来为大家详细介绍一下制作的步骤。 首先,我…...

jenkins中配置了发送邮件,构建后却没有发邮件Not sent to the following valid addresse
【问题描述】:jekins中配置了发送邮件,构建后却没有发邮件的问题,构建报错:Not sent to the following valid addresse 【报错显示】: 【问题定位】:Extended E-mail Notification中,没有配置…...

装箱问题(背包问题)
题目描述 有一个箱子容量为v(正整数,o≤v≤20000),同时有n个物品(o≤n≤30),每个物品有一个体积 (正整数)。要求从 n 个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。 输入格式 第一行,一个整…...

【C++】总结4-this指针
文章目录 什么是this指针this指针存在的意义this指针的特性this指针存在哪里this指针可以为空吗 什么是this指针 C编译器给每个非静态成员函数增加了一个隐藏的指针参数,让该指针指向当前对象(函数运行时调用该函数的对象),在函数…...

go压力测试
压力测试 1.1.1. Go怎么写测试用例 开发程序其中很重要的一点是测试,我们如何保证代码的质量,如何保证每个函数是可运行,运行结果是正确的,又如何保证写出来的代码性能是好的,我们知道单元测试的重点在于发现程序设计…...
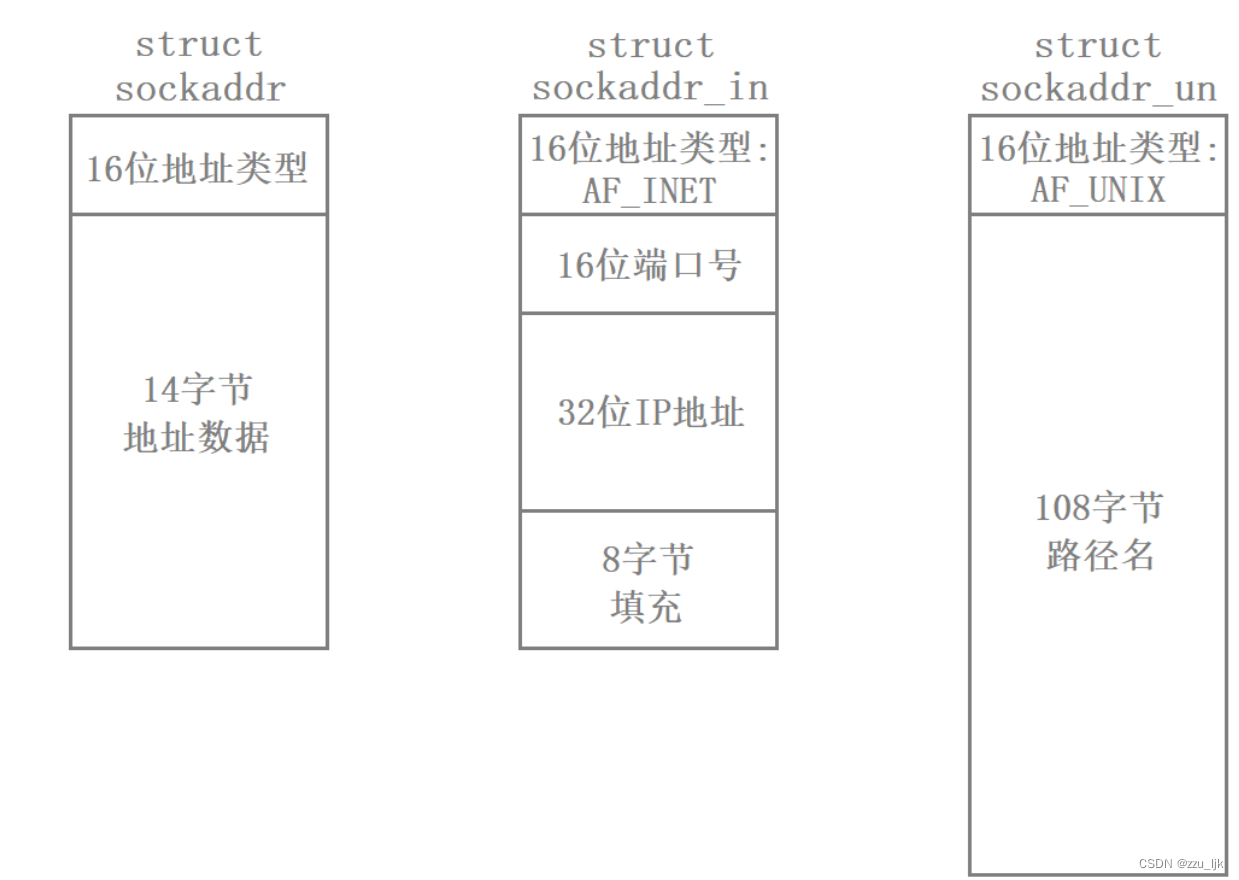
【计算机网络】socket编程基础
文章目录 1. 源IP地址和目的IP地址2. 理解MAC地址和目的MAC地址3. 理解源端口号和目的端口号4. PORT与PID5. 认识TCP协议和UDP协议6. 网络字节序7. socket编程接口7.1 socket常见API7.2 sockaddr结构 1. 源IP地址和目的IP地址 因特网上的每台计算机都有一个唯一的IP地址&#…...
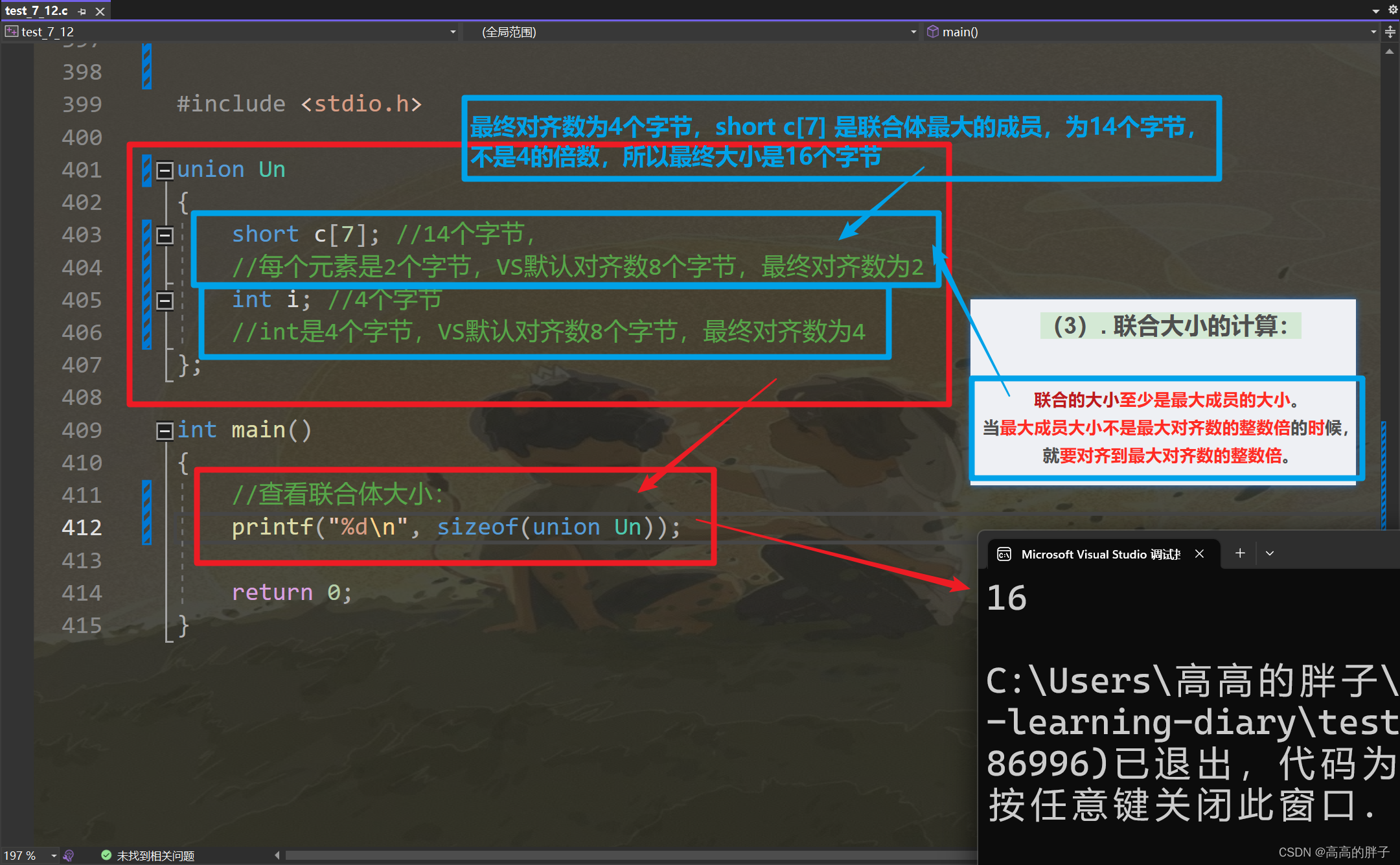
学C的第三十天【自定义类型:结构体、枚举、联合】
相关代码gitee自取:C语言学习日记: 加油努力 (gitee.com) 接上期: 学C的第二十九天【字符串函数和内存函数的介绍(二)】_高高的胖子的博客-CSDN博客 1 . 结构体 (1). 结构体的基础知识: 结构…...
:通过noVNC实现网页访问vnc)
Ubuntu(20.04):通过noVNC实现网页访问vnc
VNC vnc是日常工作和生产环境中常用的远程桌面控制工具。 通常需要在被访问的系统中安装vncserver。 然后在发起访问端,安装客户端软件,比如VNC Viewer。 noVNC noVNC提供了一种方案,就是通过web浏览器直接访问vnc server。 其实现的基本原理是: 1.已经安装好的vncse…...

OpenAI的Function calling 和 LangChain的Search Agent
OpenAI的Function calling openai最近发布的gpt-3.5-turbo-0613 和 gpt-4-0613版本模型增加了function calling的功能,该功能通过定义功能函数,gpt通过分析问题和函数功能描述来决定是否调用函数,并且生成函数对应的入参。函数调用的功能可以…...

【mysql数据库】MySQL7在Centos7的环境安装
说明: 安装与卸载中,用户全部切换成为root,⼀旦安装,普通用户就能使用。初期练习,mysql不进行用户管理,全部使⽤root进⾏,尽快适应mysql语句,后⾯学了用户管理,在考虑新…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
