分布式理论:CAP理论 BASE理论
文章目录
- 1. CAP定理
- 1.1 一致性
- 1.2 可用性
- 1.3 分区容错
- 1.4 矛盾
- 2. BASE理论
- 3. 解决分布式事务的思路
- 4. 扩展

解决分布式事务问题,需要一些分布式系统的基础知识作为理论指导。
1. CAP定理
Consistency(一致性): 用户访问分布式系统中的任意节点,得到的数据必须一致 Availability(可用性):
用户访问集群中的任意健康节点,必须能得到响应,而不是超时或拒绝。 Partition(分区):
因为网络故障或其它原因导致分布式系统中的部分节点与其它节点失去连接,形成独立分区。 tolerance(容错):
在集群出现分区时,整个系统也要持续对外提供服务
======结论: CP : 强一致性,弱可用性(牺牲部分机器的可用性,保证数据一致性) AP : 强可用性,弱一致性(牺牲一致性,保证可用性)
1998年,加州大学的计算机科学家 Eric Brewer 提出,分布式系统有三个指标。
- Consistency(一致性)
- Availability(可用性)
- Partition tolerance (分区容错性)
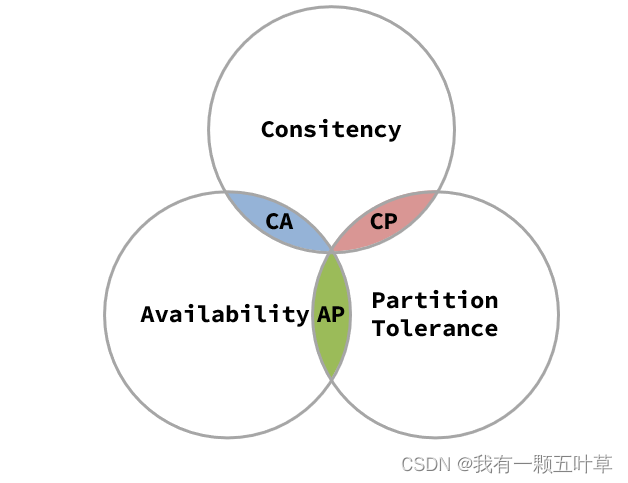
它们的第一个字母分别是 C、A、P。
Eric Brewer 说,这三个指标不可能同时做到。这个结论就叫做 CAP 定理。
1.1 一致性
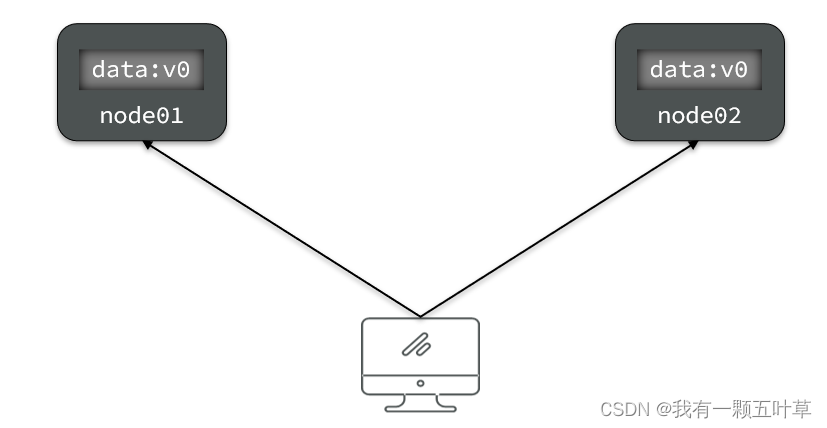
Consistency(一致性):用户访问分布式系统中的任意节点,得到的数据必须一致。
比如现在包含两个节点,其中的初始数据是一致的:
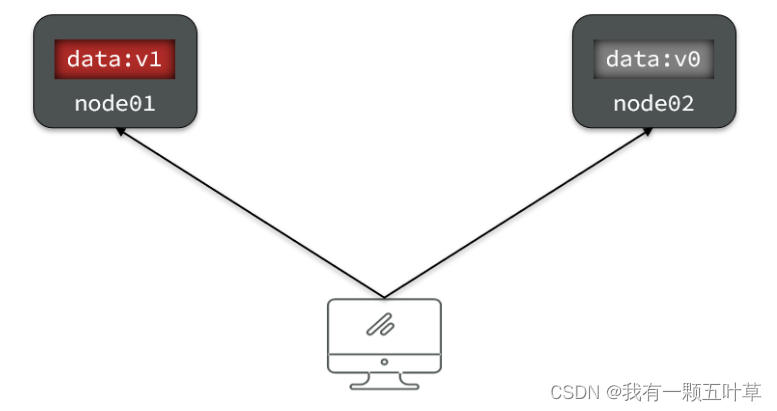
当我们修改其中一个节点的数据时,两者的数据产生了差异:
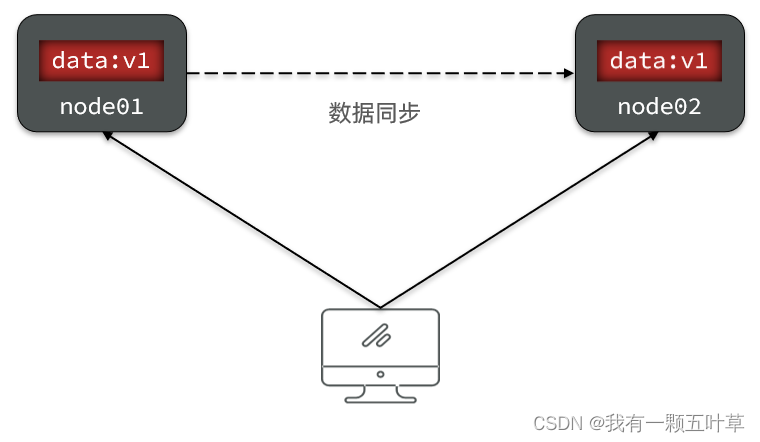
要想保住一致性,就必须实现node01 到 node02的数据 同步:
1.2 可用性
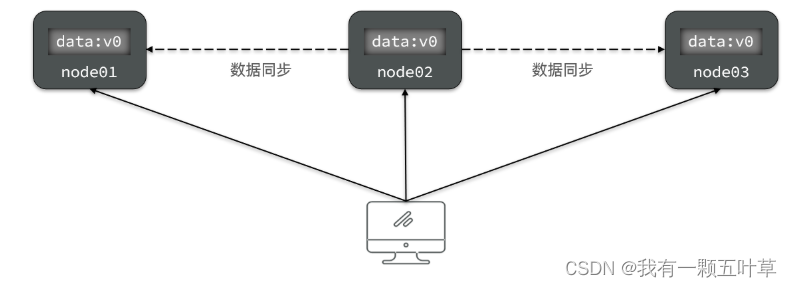
Availability (可用性):用户访问集群中的任意健康节点,必须能得到响应,而不是超时或拒绝。
如图,有三个节点的集群,访问任何一个都可以及时得到响应:
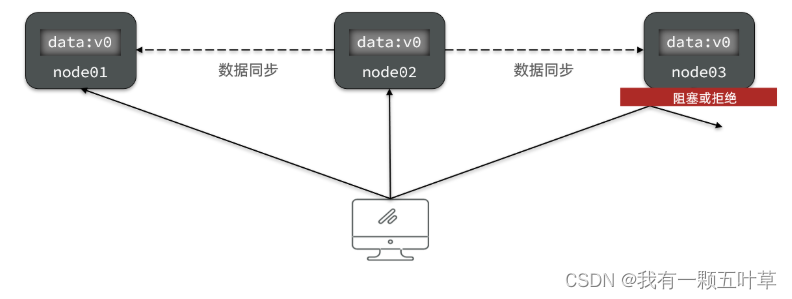
当有部分节点因为网络故障或其它原因无法访问时,代表节点不可用:
1.3 分区容错
Partition(分区):因为网络故障或其它原因导致分布式系统中的部分节点与其它节点失去连接,形成独立分区。
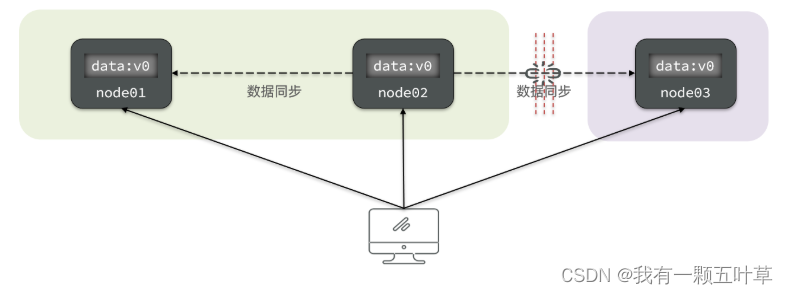
Tolerance(容错):在集群出现分区时,整个系统也要持续对外提供服务
1.4 矛盾
在分布式系统中,系统间的网络不能100%保证健康,一定会有故障的时候,而服务有必须对外保证服务。因此Partition Tolerance不可避免。
当节点接收到新的数据变更时,就会出现问题了:
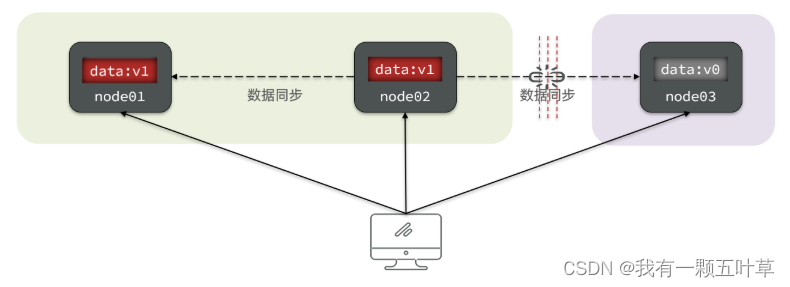
如果此时要保证一致性,就必须等待网络恢复,完成数据同步后,整个集群才对外提供服务,服务处于阻塞状态,不可用。
如果此时要保证可用性,就不能等待网络恢复,那node01、node02与node03之间就会出现数据不一致。
也就是说,在P一定会出现的情况下,A和C之间只能实现一个。
2. BASE理论
BASE理论是对CAP的一种解决思路,包含三个思想:
- Basically Available (基本可用):分布式系统在出现故障时,允许损失部分可用性,即保证核心可用。
- Soft State(软状态) 在一定时间内,允许出现中间状态,比如临时的不一致状态。
- Eventually Consistent(最终一致性):虽然无法保证强一致性,但是在软状态结束后,最终达到数据一致。
3. 解决分布式事务的思路
分布式事务最大的问题是各个子事务的一致性问题,因此可以借鉴CAP定理和BASE理论,有两种解决思路:
-
AP模式:各子事务分别执行和提交,允许出现结果不一致,然后采用弥补措施恢复数据即可,实现最终一致。
-
CP模式:各个子事务执行后互相等待,同时提交,同时回滚,达成强一致。但事务等待过程中,处于弱可用状态。
但不管是哪一种模式,都需要在子系统事务之间互相通讯,协调事务状态,也就是需要一个事务协调者(TC):
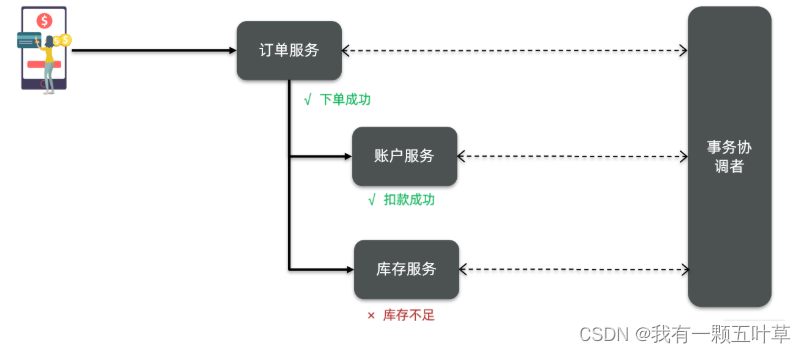
这里的子系统事务,称为分支事务;有关联的各个分支事务在一起称为全局事务。
4. 扩展
ES 是 CP 为主,ES集群有节点发生故障 会剔除故障节点,数据会重新分配到其他节点,这个过程集群是不可用的保证数据的一致性。因此是低可用性、高一致性。
Eureka 是 AP。
Nacos 是有 CP 和 AP 都支持(默认AP)。

相关文章:

分布式理论:CAP理论 BASE理论
文章目录 1. CAP定理1.1 一致性1.2 可用性1.3 分区容错1.4 矛盾 2. BASE理论3. 解决分布式事务的思路4. 扩展 解决分布式事务问题,需要一些分布式系统的基础知识作为理论指导。 1. CAP定理 Consistency(一致性): 用户访问分布式系统中的任意节点,得到的…...

Tensorflow学习
一、处理数据的结构 案例代码如下: import tensorflow.compat.v1 as tf tf.disable_v2_behavior() import numpy as np# create data x_data np.random.rand(100).astype(np.float32) y_data x_data*0.1 0.3# 创建结构(一维结构) Weights tf.Variable(tf.random.uniform(…...
5-Ngnix配置基于用户访问控制和IP的虚拟主机
目录 5.1.Ngnix配置基于用户访问控制的多虚拟主机 5.1.1.前提条件 5.1.2.Ngnix配置基于用户访问控制的多虚拟主机 5.2.Ngnix配置基于IP的虚拟主机 5.3.Ngnix配置基于IP的多虚拟主机 Nginx配置文件在/usr/local/nginx/conf下,文件名为nginx.conf 5.1.Ngnix配置…...

springboot jar分离部署
springboot jar分离部署 注意:spring boot web项目别使用jsp页面,可以使用模板代替,jsp打包时访问页面会报404错误。 1.具体配置如下: <build><plugins><!--更换maven的jar打包插件先前使用的是spring-boot-mav…...

Opencv 细节补充
1.分辨率的解释 •像素:像素是分辨率的单位。像素是构成位图图像最基本的单元,每个像素都有自己的颜色。 •分辨率(解析度): a) 图像分辨率就是单位英寸内的像素点数。单位为PPI(Pixels Per Inch) b) PPI表示的是每英…...
hook之宏定义)
内存泄漏专题(7)hook之宏定义
前面介绍的mtrace也好,bcc也罢,其实都是hook技术的一种实现,但是mtrace本身使用场景上有局限,而bcc环境依赖则十分复杂。因此,这些调试手段只适用于开发环境用来调试,对于生产环境,均不是一个非…...

Python 基础(十八):异常处理
❤️ 博客主页:水滴技术 🌸 订阅专栏:Python 入门核心技术 🚀 支持水滴:点赞👍 收藏⭐ 留言💬 文章目录 一、异常是什么?二、异常处理的基本语法三、捕获特定的异常类型四、finall…...

iTOP-RK3568开发板Docker 安装 Ubuntu 18.04
Docker 下载安装 Ubuntu18.04,输入以下命令: sudo apt update docker pull ubuntu:18.04 切换 Shell 到 Ubuntu 18.04,输入以下命令: docker container run -p 8000:3000 -it ubuntu:18.04 /bin/bash -p 参数:容器的…...
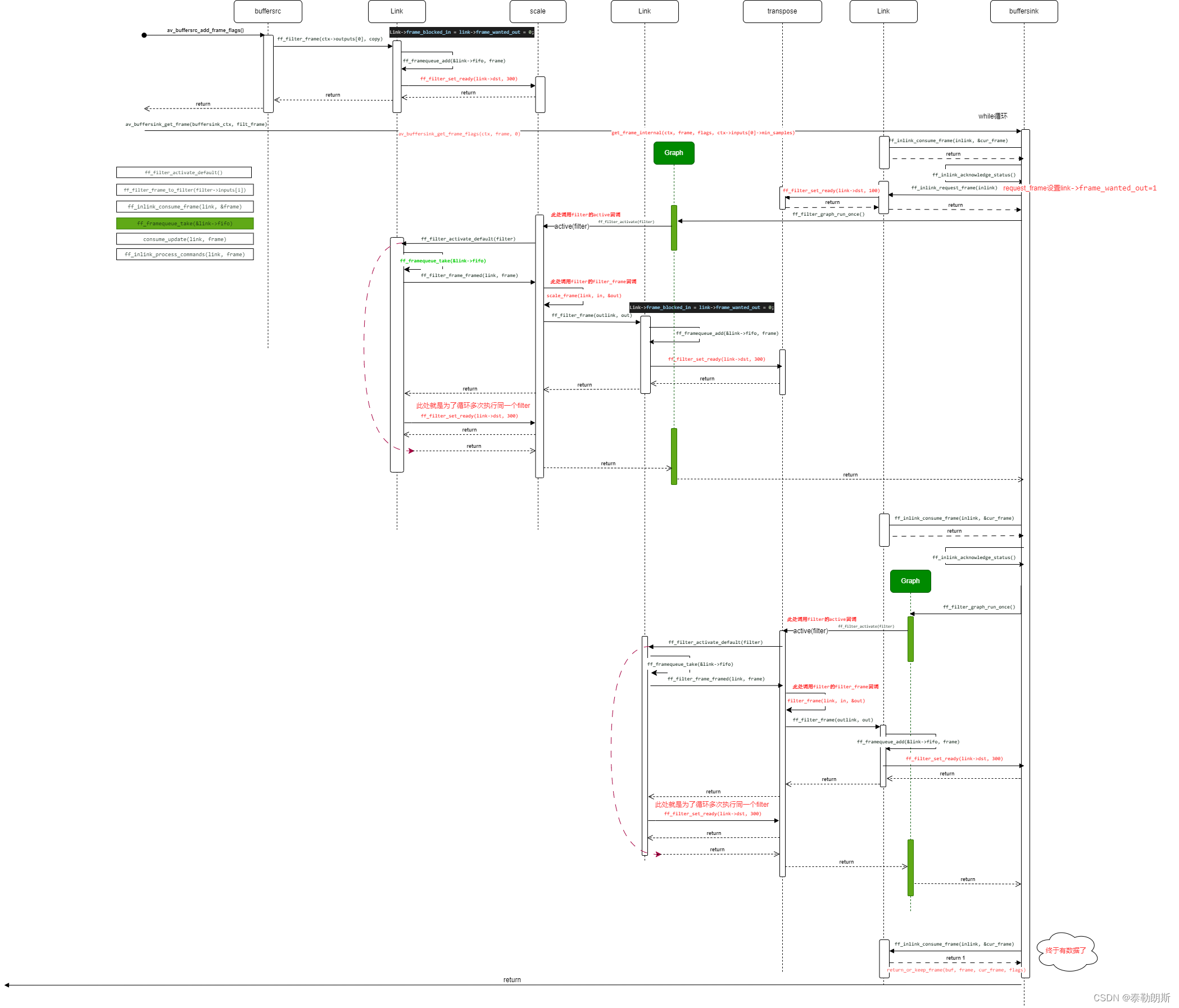
FFmpeg AVFilter的原理(三)- filter是如何被驱动的
首先上官方filter的链接:https://ffmpeg.org/ffmpeg-filters.html 关于filter命令行:FFmpeg-4.0 的filter机制的架构与实现.之一 Filter原理 1、下面是一个avfilter的graph 上图是ffmpeg中doc/examples中filtering_video.c案例的示意图。 特别注意上面蓝…...
ARM day8 key1/2/3led
key_led.h #ifndef _KEY_H_ #define _KEY_H_#include "stm32mp1xx_rcc.h" #include "stm32mp1xx_gpio.h" #include "stm32mp1xx_exti.h" #include "stm32mp1xx_gic.h"//EXTI编号 typedef enum {EXTI0,EXTI1,EXTI2,EXTI3,EXTI4,EXTI5,…...
windows 系统安装sonarqube
SonarQube是一种自动代码审查工具,用于检测代码中的错误,漏洞和代码异味。它可以与您现有的工作流程集成,以便在项目分支和拉取请求之间进行连续的代码检查。 官方网站: https://www.sonarqube.org/ 1. 使用前提条件 运行SonarQ…...
Unity噪声图生成(编辑器扩展)
最近发现项目里很多shader都需要噪声图,(shadergraph中有自己的噪声图生成)当遇到需要噪声图时去寻找很麻烦,所以从网上查阅资料编写了一个Unity扩展的噪声图生成。 Perlin噪声 Perlin噪声是一种渐变噪声算法,由Ken …...

http-为什么文件上传要转成Base64
# 前言 最近在开发中遇到文件上传采用Base64的方式上传,记得以前刚开始学http上传文件的时候,都是通过content-type为multipart/form-data方式直接上传二进制文件,我们知道都通过网络传输最终只能传输二进制流,所以毫无疑问他们本…...

htmlCSS-----定位
目录 前言 定位 分类和取值 定位的取值 1.相对定位 2.绝对位置 元素居中操作 3.固定定位 前言 今天我们来学习html&CSS中的元素的定位,通过元素的定位我们可以去更好的将盒子放到我们想要的位置,下面就一起来看看吧! 定位 定位posi…...

腾讯云大数据型CVM服务器实例D3和D2处理器CPU型号说明
腾讯云服务器CVM大数据型D3和D2处理器型号,大数据型D3云服务器CPU采用2.5GHz Intel Xeon Cascade Lake 处理器,大数据型D2云服务器CPU采用2.4GHz Intel Xeon Skylake 6148 处理器。腾讯云服务器网分享云服务器CVM大数据型CPU型号、处理器主频性能&#x…...
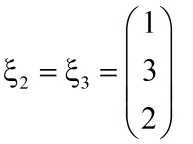
计算机科学cs/电子信息ei面试准备——数学基础/线性代数复习
1. 中值定理 中值定理是反映函数与导数之间联系的重要定理,也是微积分学的理论基础,在许多方面它都有重要的作用,在进行一些公式推导与定理证明中都有很多应用。中值定理是由众多定理共同构建的,其中拉格朗日中值定理是核心&…...
-算法分析)
极速查找(2)-算法分析
篇前小言 本篇文章是对查找(1)的续讲线性索引查找 线性索引查找(Linear Index Search)是一种基于索引的查找算法。它在数据集合中创建一个索引 结构,然后使用该索引结构来加快对目标元素的查找。 线性索引是一种在数…...

flask路由添加参数
flask路由添加参数 在 Flask 中,可以通过两种方式在路由中添加参数:在路由字符串中直接指定参数,或者通过 request 对象从请求中获取参数。 在路由字符串中指定参数:可以将参数直接包含在路由字符串中。参数可以是字符串、整数、…...

网络安全系统教程+学习路线(自学笔记)
一、什么是网络安全 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 无论网络、Web、移动、桌面、云等哪个领域,都有攻与防两面…...

23. 合并 K 个升序链表
题目描述 给你一个链表数组,每个链表都已经按升序排列。 请你将所有链表合并到一个升序链表中,返回合并后的链表。 示例 1: 输入:lists [[1,4,5],[1,3,4],[2,6]] 输出:[1,1,2,3,4,4,5,6] 解释:链表数组…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
