godot引擎c++源码深度解析系列一
许久没有使用c++开发过项目了,如果按照此时单位的入职要求,必须拥有项目经验的话,那我就得回到十多年前,大学的时代,哪个时候真好,电脑没有这么普及,手机没有这么智能,网络没有这么发达,信息传播没有此时的快,哪个年代,5毛钱一份的报纸或许真的很好。学习技术只能靠阅读大量的书籍来获取经验。
入职it这个行业以来,想必很多的同行,前辈们,都知道,软件开发唯一的要求,实践能力必须很强,不亲自实操,你永远不知道代码里有多少个坑,同样的一段代码,在A电脑能运行,在B电脑就运行不了,这就是环境对此的影响。
此时,看看身边的同事们,各有千秋,而自己呢,确又回到了当初。
Godot是一个开源的跨平台游戏引擎,用于开发2D和3D游戏。它由一个专注于游戏开发的非营利组织开发和维护。以下是一些关于Godot的示例代码:
extends Node2Dfunc _ready():var sprite = Sprite.new()sprite.texture = load("res://texture.png")add_child(sprite)
看了上述的代码是不是觉得很有熟悉的感觉,很简单。No,No,No,后面的还有很多。我们先来看下开发工具界面

这个界面看起来还是很舒服的,如果你觉得不舒服,没有问题,打开源码,咱自己修改。前面说过godot是一个开源的游戏引擎,既然开源,那么我们就从源代码里来修改他的界面,看能否实现。

源码我们已经下载好了,如果你还没下载的话,可以参考下方的地址。
- 官方网站:Godot Engine - Free and open source 2D and 3D game engine
- 官方文档:Godot Docs – 4.1 branch — Godot Engine (stable) documentation in English
- GitHub仓库:GitHub - godotengine/godot: Godot Engine – Multi-platform 2D and 3D game engine
看到上述的源码结构,确又不知道从哪里入手了,毕竟好久没有使用c++了,还好凭借着大脑中仅存的一点记忆,找到了程序的入口文件,开启了我阅读源码的路程。

既然找到了熟悉的感觉,那就开启第一个尝试,就是增加一个功能,实现用户打字练习的功能。

经过漫长的一天,总算是有些模样了,虽然丑点,但至少知道从哪里入口了。
当然了研究源码的目的不仅仅只是为了增加一个打字练习的窗口,还有好多的功能要实现,用一句话来表示那就是““路漫漫其修远兮,吾将上下而求索”。

Finally, after a day of tossing and turning, I used all my years of college experience, communicating in English, and returning to the original development language C++. Although ten years have passed, everything seems to be yesterday.。
相关文章:

godot引擎c++源码深度解析系列一
许久没有使用c开发过项目了,如果按照此时单位的入职要求,必须拥有项目经验的话,那我就得回到十多年前,大学的时代,哪个时候真好,电脑没有这么普及,手机没有这么智能,网络没有这么发达…...
【VB6|第21期】检查SqlServer数据库置疑损坏的小工具(含源码)
日期:2023年7月25日 作者:Commas 签名:(ง •_•)ง 积跬步以致千里,积小流以成江海…… 注释:如果您觉得有所帮助,帮忙点个赞,也可以关注我,我们一起成长;如果有不对的地方…...

React的hooks---useCallback useMemo
useCallback 和 useMemo 结合 React.Memo 方法的使用是常见的性能优化方式,可以避免由于父组件状态变更导致不必要的子组件进行重新渲染 useCallback useCallback 用于创建返回一个回调函数,该回调函数只会在某个依赖项发生改变时才会更新,…...
05. 容器资源管理
目录 1、前言 2、CGroup 2.1、是否开启CGroup 2.2、Linux CGroup限制资源能使用 2.2.1、创建一个demo 2.2.2、CGroup限制CPU使用 2.3、Linux CGroup限制内存使用 2.4、Linux CGroup限制IO 3、Docker对资源的管理 3.1、Docker对CPU的限制 3.1.1、构建一个镜像 3.1.2…...
通过ETL自动化同步飞书数据到本地数仓
一、飞书数据同步到数据库需求 使用飞书的企业都有将飞书的数据自动同步到本地数据库、数仓以及其他业务系统表的需求,主要是为了实现飞书的数据与业务系统进行流程拉通或数据分析时使用,以下是一些具体的同步场景示例: 组织架构同步&#…...

MySQL基础扎实——MySQL中各种数据类型之间的区别
在MySQL中,有各种不同的数据类型可供选择来存储不同类型的数据。下面是一些常见的数据类型以及它们之间的区别: 整数类型: TINYINT:1字节,范围为-128到127或0到255(无符号)。SMALLINT࿱…...
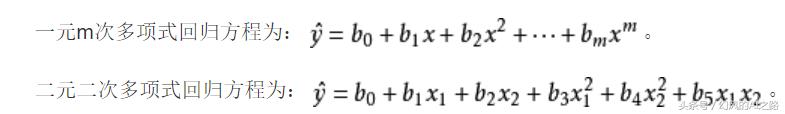
每天五分钟机器学习:多项式非线性回归模型
本文重点 在前面的课程中,我们学习了线性回归模型和非线性回归模型的区别和联系。多项式非线性回归模型是一种用于拟合非线性数据的回归模型。与线性回归模型不同,多项式非线性回归模型可以通过增加多项式的次数来适应更复杂的数据模式。在本文中,我们将介绍多项式非线性回…...

ETH网络学习
概要 ETH网络是一个P2P网络,整个网络又区分为“执行层”与“共识层”。“执行层”节点负责交易交换,“共识层”节点负责区块打包、区块验证、区块同步和链同步。 执行层 执行层分为“服务发现”与“DevP2P”,两者共同并行执行。 服务发现…...

01-将函数参数化进行传递
项目源码:https://github.com/java8/ 1 应对不断变化的需求 在我们进行开发中,经常需要面临需求的不断变更,我们可以将行为参数化以适应不断变更的需求。 行为参数化就是可以帮助我们处理频繁变更的需求的一种软件开发模式 我们可以将代码…...
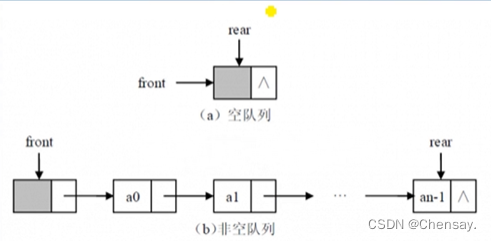
数据结构【栈和队列】
第三章 栈与队列 一、栈 1.定义:只允许一端进行插入和删除的线性表,结构与手枪的弹夹差不多,可以作为实现递归函数(调用和返回都是后进先出)调用的一种数据结构; 栈顶:允许插入删除的那端&…...
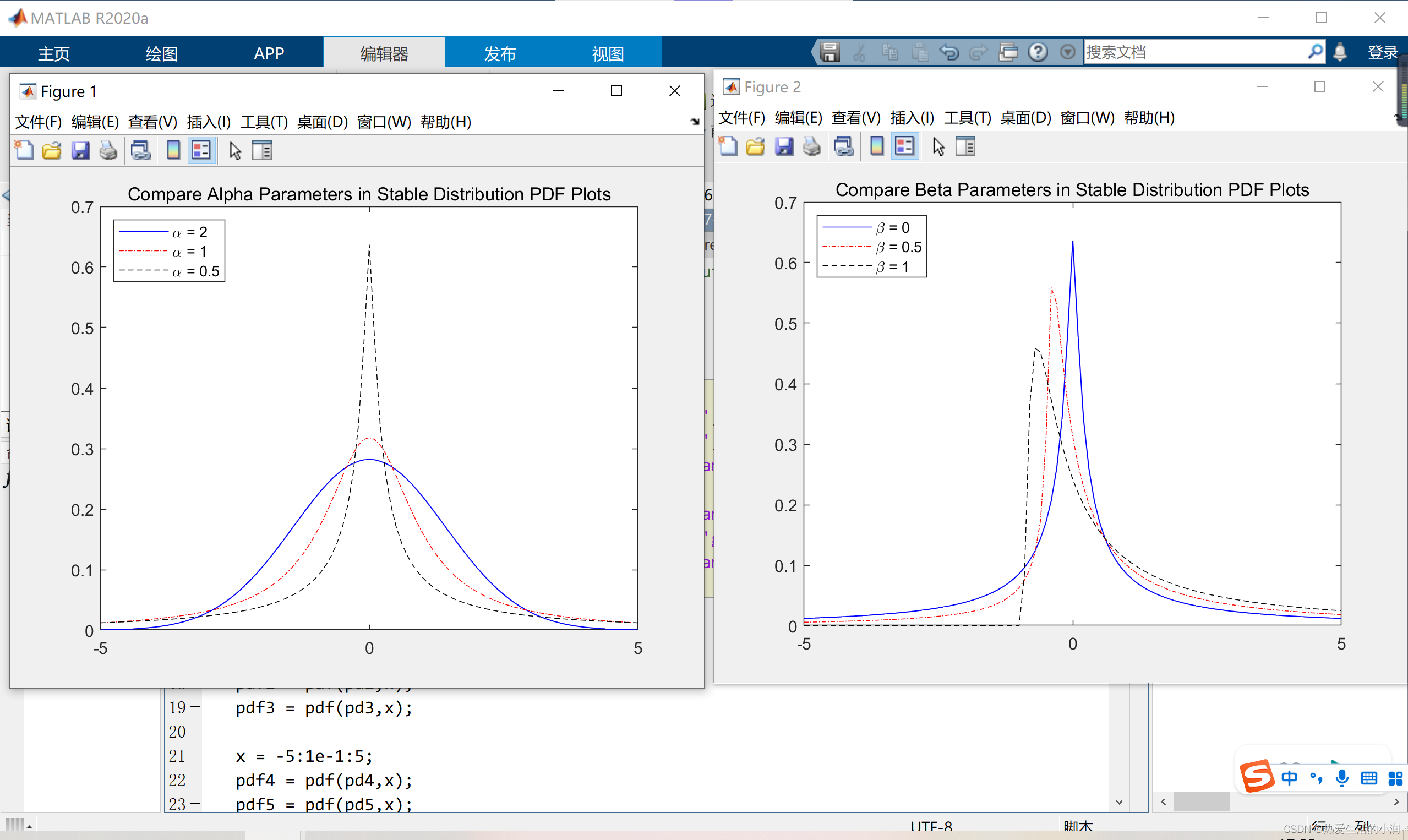
MATLAB | 产生阿尔法稳定分布噪声并作出概率密度函数
一、问题描述 想产生不同特征参数的α稳定随机变量,并且作出其概率密度函数进行对比。 二、解决思路 运行了MATLAB的官方实例代码: openExample(‘stats/ComparePDFsOfStableDistributionsExample’) (1)使用makedist()函数生成…...

深入浅出Pytorch函数——torch.softmax/torch.nn.functional.softmax
分类目录:《深入浅出Pytorch函数》总目录 相关文章: 机器学习中的数学——激活函数:Softmax函数 深入浅出Pytorch函数——torch.softmax/torch.nn.functional.softmax 深入浅出Pytorch函数——torch.nn.Softmax 将Softmax函数应用于沿dim的…...

Vue2学习笔记
vue是根据数据来构建用户界面的一套框架 创建一个vue实例 <!-- 1.创建一个容器 2.引入vue.js开发版本(全局的) 3.创建实例对象 4.配置选项 > 完成渲染 --> <div id"app">{{ msg }} </div> <script srcvue.js><…...
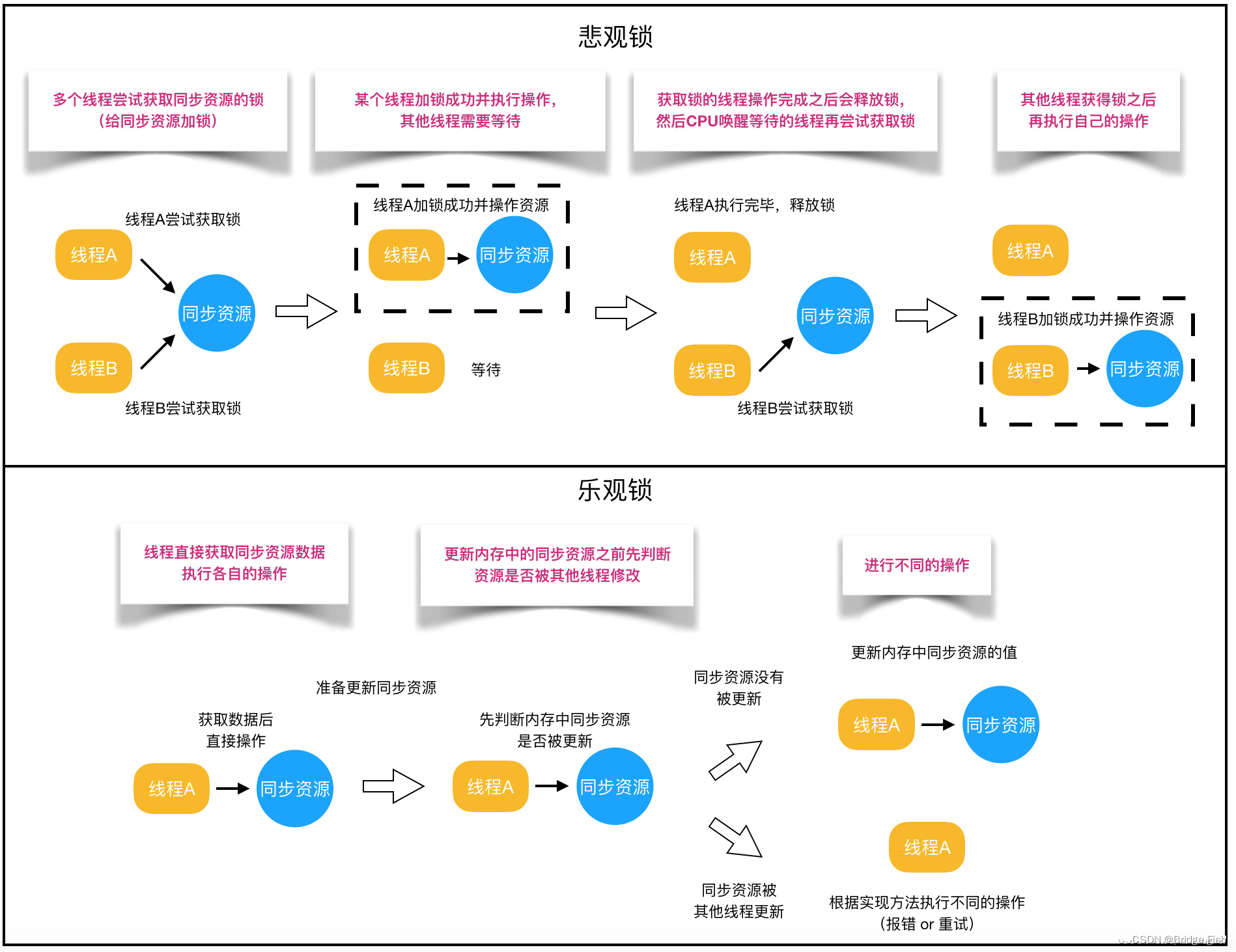
Java 悲观锁 乐观锁
锁可以从不同的角都分类。其中乐观锁和悲观锁是一种分类方式 一、悲观锁、乐观锁定义 悲观锁就是我们常说到的锁。对于悲观锁来说,他总是认为每次访问共享资源时会发生冲突,所以必须每次数据操作加上锁,以保证临界区的程序同一时间只能有一个…...
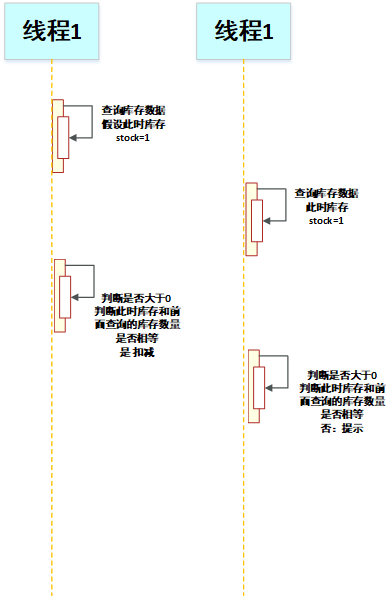
优惠券秒杀(二)
库存超卖问题分析 库存超卖问题其本质就是多个线程操作共享数据产生的线程安全问题,即当一个线程在执行操作共享数据的多条代码的过程中,其他线程也参与了进来,导致了线程安全问题的产生。例如:线程1发送请求,查询库存…...
selenium的java方式打开IE浏览器
1.下载软件Selenium Driver 官方下载地址: https://www.selenium.dev/downloads/解压selenium-java-3.141.59.zip文件到java项目 seleniumDemo,并降解压的文件放入依赖中(1)双击项目的src打开项目结构,或右键-打开…...

分类评估指标
文章目录 1. 混淆矩阵2. Precision(精准率)3. Recall(召回率)4. F1-score5. ROC曲线和AUC指标5.1 ROC 曲线5.2 绘制 ROC 曲线5.3 AUC 值6. API介绍6.1 **分类评估报告api**6.2 **AUC计算API**练习-电信客户流失预测1. 数据集介绍2. 处理流程3. 案例实现4. 小结1. 混淆矩阵 …...
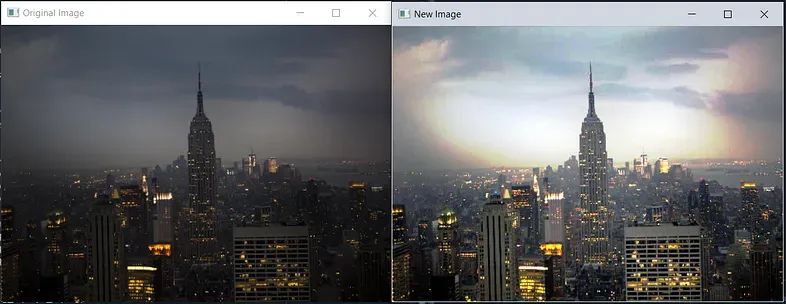
OpenCV:图像直方图计算
图像直方图为图像中像素强度的分布提供了有价值的见解。通过了解直方图,你可以获得有关图像对比度、亮度和整体色调分布的信息。这些知识对于图像增强、图像分割和特征提取等任务非常有用。 本文旨在为学习如何使用 OpenCV 执行图像直方图计算提供清晰且全面的指南。…...

用QFramework来重构 祖玛游戏
资料 Unity - 祖玛游戏 GitHub 说明 用QF一个场景就够了,在UIRoot下切换预制体达到面板切换。 但测试中当然要有一个直接跳到测试面板的 测试脚本,保留测试Scene(不然初学者也不知道怎么恢复测试Scene),所以全文按S…...

生活杂记-显示器尺寸
以下是常见显示器尺寸的对角线长度换算成厘米的结果(已经四舍五入到最接近的厘米数): 19英寸显示器 ≈ 48.26厘米21.5英寸显示器 ≈ 54.61厘米24英寸显示器 ≈ 60.96厘米27英寸显示器 ≈ 68.58厘米32英寸显示器 ≈ 81.28厘米34英寸显示器 ≈…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
