GBDT的参数空间与超参数优化
目录
1. 默认参数下的GBDT与其它算法的对比
2. 基于TPE对GBDT进行优化
step1:建立benchmark
step2:定义参数init需要的算法
step3:定义目标函数、参数空间、优化函数、验证函数
step4:训练贝叶斯优化器
step5:修改搜索空间
step6:继续修改搜索空间
丰富的超参数为集成算法提供了无限的可能,以降低偏差为目的的Boosting算法们在调参之后的表现更是所向披靡,因此GBDT的超参数自动优化也是一个重要的课题。对任意集成算法进行超参数优化之前,需要明确两个基本事实:①不同参数对算法结果的影响力大小;②确定用于搜索的参数空间。对GBDT来说,可以大致如下排列各个参数对算法的影响:
| 影响力 | 参数 |
|---|---|
| ⭐⭐⭐⭐⭐ 几乎总是具有巨大影响力 | n_estimators(整体学习能力) learning_rate(整体学习速率) max_features(随机性) |
| ⭐⭐⭐⭐ 大部分时候具有影响力 | init(初始化) subsamples(随机性) loss(整体学习能力) |
| ⭐⭐ 可能有大影响力 大部分时候影响力不明显 | max_depth(粗剪枝) min_samples_split(精剪枝) min_impurity_decrease(精剪枝) max_leaf_nodes(精剪枝) criterion(分枝敏感度) |
| ⭐ 当数据量足够大时,几乎无影响 | random_state ccp_alpha(结构风险) |
树的集成模型们大多拥有相似的超参数,例如抗过拟合、用来剪枝的参数群(max_depth、min_samples_split等),又比如对样本/特征进行抽样的参数们(subsample,max_features等),这些超参数在不同的集成模型中以相似的方式影响模型,因此原则上来说,对随机森林影响较大的参数对GBDT也会有较大的影响。然而,在随机森林中非常关键的max_depth在GBDT中没有什么地位,取而代之的是Boosting中特有的迭代参数学习率learning_rate。在随机森林中,我们总是在意模型复杂度(max_depth)与模型整体学习能力(n_estimators)的平衡,单一弱评估器的复杂度越大,单一弱评估器对模型的整体贡献就越大,因此需要的树数量就越少。在Boosting算法当中,单一弱评估器对整体算法的贡献由学习率参数learning_rate控制,代替了弱评估器复杂度的地位,因此Boosting算法中我们寻找的是learning_rate与n_estimators的平衡。同时,Boosting算法天生就假设单一弱评估器的能力很弱,参数max_depth的默认值也往往较小(在GBDT中max_depth的默认值是3),因此我们无法靠降低max_depth的值来大规模降低模型复杂度,更难以靠max_depth来控制过拟合,自然max_depth的影响力就变小了。可见,虽然树的集成算法们大多共享相同的超参数,都由于不同算法构建时的原理假设不同,相同参数在不同算法中的默认值可能被设置得不同,因此相同参数在不同算法中的重要性和调参思路也不同。
在解随机森林中,精剪枝工具的效用有限,剪枝一般还是大刀阔斧的粗剪枝更有效。在GBDT中,由于max_depth这一粗剪枝工具的默认值为3,因此在Boosting算法中通过削减模型复杂度来控制过拟合的思路就无法走通。特别地,参数init对GBDT的影响很大,如果在参数init中填入具体的算法,过拟合可能会变得更加严重,因此我们需要在抑制过拟合、控制复杂度这一点上令下功夫。如果无法对弱评估器进行剪枝,最好的控制过拟合的方法就是增加随机性/多样性,因此max_features和subsample就成为Boosting算法中控制过拟合的核心武器,这也是GBDT中会加入Bagging思想的关键原因之一。依赖于随机性、而非弱评估器结构来对抗过拟合的特点,让Boosting算法获得了一个意外的优势:比起Bagging,Boosting更加擅长处理小样本高维度的数据,因为Bagging数据很容易在小样本数据集上过拟合。
需要注意的是,虽然max_depth在控制过拟合上的贡献不大,但是我们在调参时依然需要保留这个参数。当我们使用参数max_features与subsample构建随机性、并加大每一棵树之间的差异后,模型的学习能力可能受到影响,因此我们可能需要提升单一弱评估器的复杂度。因此在GBDT当中,max_depth的调参方向是放大/加深,以探究模型是否需要更高的单一评估器复杂度。相对的在随机森林当中,max_depth的调参方向是缩小/剪枝,用以缓解过拟合。
那在调参的时候,我们应该选择哪些参数呢?首先考虑所有影响力巨大的参数,当算力足够/优化算法运行较快的时候,我们可以考虑将大部分时候具有影响力的参数也都加入参数空间,如果样本量较小,我们可能不选择subsample。除此之外,我们还需要部分影响弱评估器复杂度的参数,例如max_depth。如果算力充足,我们还可以加入criterion这样或许会有效的参数。在这样的基本思想下,考虑到硬件与运行时间因素,这里将选择如下参数进行调整,并使用基于TPE贝叶斯优化(HyperOpt)对GBDT进行优化:
| 参数 | 范围 |
|---|---|
loss | 回归损失中4种可选损失函数 ["squared_error","absolute_error", "huber", "quantile"] |
criterion | 全部可选的4种不纯度评估指标 ["friedman_mse", "squared_error"] |
init | HyperOpt不支持搜索,手动调参 |
n_estimators | 经由提前停止确认中间数50,最后范围定为(25,200,25) |
learning_rate | 以1.0为中心向两边延展,最后范围定为(0.05,2.05,0.05) 如果算力有限,也可定为(0.1,2.1,0.1) |
max_features | 所有字符串,外加sqrt与auto中间的值 |
subsample | subsample参数的取值范围为(0,1],因此定范围(0.1,0.8,0.1) 如果算力有限,也可定为(0.5,0.8,0.1) |
max_depth | 以3为中心向两边延展,右侧范围定得更大。最后确认(2,30,2) |
min_impurity_decrease | 只能放大、不能缩小的参数,先尝试(0,5,1)范围 |
一般在初次搜索时,我们会设置范围较大、较为稀疏的参数空间,然后在多次搜索中逐渐缩小范围、降低参数空间的维度。需要注意的是,init参数中需要输入的评估器对象无法被HyperOpt库识别,因此参数init我们只能手动调参。
1. 默认参数下的GBDT与其它算法的对比
导入所需库和数据:
import pandas as pd
import numpy as np
import sklearn
import matplotlib as mlp
import matplotlib.pyplot as plt
import time
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.ensemble import GradientBoostingRegressor as GBR
from sklearn.ensemble import AdaBoostRegressor as ABR
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.model_selection import cross_validate, KFold#导入优化算法
import hyperopt
from hyperopt import hp, fmin, tpe, Trials, partial
from hyperopt.early_stop import no_progress_lossdata = pd.read_csv(r"F:\\Jupyter Files\\机器学习进阶\\datasets\\House Price\\train_encode.csv",index_col=0)
X = data.iloc[:,:-1]
y = data.iloc[:,-1]
X.shape #(1460, 80)cv = KFold(n_splits=5,shuffle=True,random_state=1412)def RMSE(result,name):return abs(result[name].mean())
modelname = ["GBDT","RF","AdaBoost","RF-TPE","Ada-TPE"]models = [GBR(random_state=1412),RFR(random_state=1412),ABR(random_state=1412),RFR(n_estimators=89, max_depth=22, max_features=14, min_impurity_decrease=0,random_state=1412, verbose=False),ABR(n_estimators=39, learning_rate=0.94,loss="exponential",random_state=1412)]colors = ["green","gray","orange","red","blue"]
for name,model in zip(modelname,models):start = time.time()result = cross_validate(model,X,y,cv=cv,scoring="neg_root_mean_squared_error",return_train_score=True,verbose=False)end = time.time()-startprint(name)print("\t train_score:{:.3f}".format(RMSE(result,"train_score")))print("\t test_score:{:.3f}".format(RMSE(result,"test_score")))print("\t time:{:.2f}s".format(end))print("\n")
--------------------------------------------------------------------------------------
GBDTtrain_score:13990.791test_score:28783.954time:2.16sRFtrain_score:11177.272test_score:30571.267time:5.35sAdaBoosttrain_score:27062.107test_score:35345.931time:0.99sRF-TPEtrain_score:11208.818test_score:28346.673time:1.36sAda-TPEtrain_score:27401.542test_score:35169.730time:0.83s
2. 基于TPE对GBDT进行优化
step1:建立benchmark
| 算法 | RF | AdaBoost | GBDT | RF (TPE) | AdaBoost (TPE) |
|---|---|---|---|---|---|
| 5折验证 运行时间 | 5.35s | 0.99s | 2.16s | 1.36s | 0.83s |
| 最优分数 (RMSE) | 30571.267 | 35345.931 | 28783.954 | 28346.673 | 35169.73 |
step2:定义参数init需要的算法
rf = RFR(n_estimators=89, max_depth=22, max_features=14,min_impurity_decrease=0,random_state=1412, verbose=False)step3:定义目标函数、参数空间、优化函数、验证函数
① 目标函数
def hyperopt_objective(params):reg = GBR(n_estimators = int(params["n_estimators"]),learning_rate = params["lr"],criterion = params["criterion"],loss = params["loss"],max_depth = int(params["max_depth"]),max_features = params["max_features"],subsample = params["subsample"],min_impurity_decrease = params["min_impurity_decrease"],init = rf,random_state=1412,verbose=False)cv = KFold(n_splits=5,shuffle=True,random_state=1412)validation_loss = cross_validate(reg,X,y,scoring="neg_root_mean_squared_error",cv=cv,verbose=False,error_score='raise')return np.mean(abs(validation_loss["test_score"]))② 参数空间
| 参数 | 范围 |
|---|---|
loss | 回归损失中4种可选损失函数 ["squared_error","absolute_error", "huber", "quantile"] |
criterion | 全部可选的4种不纯度评估指标 ["friedman_mse", "squared_error"] |
init | HyperOpt不支持搜索,手动调参 |
n_estimators | 经由提前停止确认中间数50,最后范围定为(25,200,25) |
learning_rate | 以1.0为中心向两边延展,最后范围定为(0.05,2.05,0.05) 如果算力有限,也可定为(0.1,2.1,0.1) |
max_features | 所有字符串,外加sqrt与auto中间的值 |
subsample | subsample参数的取值范围为(0,1],因此定范围(0.1,0.8,0.1) 如果算力有限,也可定为(0.5,0.8,0.1) |
max_depth | 以3为中心向两边延展,右侧范围定得更大。最后确认(2,30,2) |
min_impurity_decrease | 只能放大、不能缩小的参数,先尝试(0,5,1)范围 |
param_grid_simple = {'n_estimators': hp.quniform("n_estimators",25,200,25),"lr": hp.quniform("learning_rate",0.05,2.05,0.05),"criterion": hp.choice("criterion",["friedman_mse", "squared_error"]),"loss":hp.choice("loss",["squared_error","absolute_error", "huber", "quantile"]),"max_depth": hp.quniform("max_depth",2,30,2),"subsample": hp.quniform("subsample",0.1,0.8,0.1),"max_features": hp.choice("max_features",["log2","sqrt",16,32,64,1.0]),"min_impurity_decrease":hp.quniform("min_impurity_decrease",0,5,1)}③ 优化函数
def param_hyperopt(max_evals=100):#保存迭代过程trials = Trials()#设置提前停止early_stop_fn = no_progress_loss(100)#定义代理模型params_best = fmin(hyperopt_objective, space = param_grid_simple, algo = tpe.suggest, max_evals = max_evals, verbose=True, trials = trials, early_stop_fn = early_stop_fn)#打印最优参数,fmin会自动打印最佳分数print("\n","\n","best params: ", params_best,"\n")return params_best, trials④ 验证函数
def hyperopt_validation(params): reg = GBR(n_estimators = int(params["n_estimators"]),learning_rate = params["learning_rate"],criterion = params["criterion"],loss = params["loss"],max_depth = int(params["max_depth"]),max_features = params["max_features"],subsample = params["subsample"],min_impurity_decrease = params["min_impurity_decrease"],init = rf,random_state=1412 #GBR中的random_state只能够控制特征抽样,不能控制样本抽样,verbose=False)cv = KFold(n_splits=5,shuffle=True,random_state=1412)validation_loss = cross_validate(reg,X,y,scoring="neg_root_mean_squared_error",cv=cv,verbose=False)return np.mean(abs(validation_loss["test_score"]))step4:训练贝叶斯优化器
params_best, trials = param_hyperopt(30) #使用小于0.1%的空间进行训练100%|████████████████████████████████████████████████| 30/30 [02:43<00:00, 5.45s/trial, best loss: 26847.550613053456]best params: {'criterion': 0, 'learning_rate': 0.05, 'loss': 0, 'max_depth': 14.0, 'max_features': 2, 'min_impurity_decrease': 3.0, 'n_estimators': 125.0, 'subsample': 0.5}
params_best #注意hp.choice返回的结果是索引,而不是具体的数字{'criterion': 0,'learning_rate': 0.05,'loss': 0,'max_depth': 14.0,'max_features': 2,'min_impurity_decrease': 3.0,'n_estimators': 125.0,'subsample': 0.5}
hyperopt_validation({'criterion': "friedman_mse",'learning_rate': 0.05,'loss': "squared_error",'max_depth': 14.0,'max_features': 16,'min_impurity_decrease': 3.0,'n_estimators': 125.0,'subsample': 0.5})26847.550613053456
不难发现,我们已经得到了历史最好分数,但GBDT的潜力远不止如此。现在我们可以根据第一次训练出的结果缩小参数空间,继续进行搜索。在多次搜索中,我发现loss参数的最优选项基本都是平方误差"squared_error",因此我们可以将该参数排除出搜索队伍。同样,对于其他参数,我们则根据搜索结果修改空间范围、增加空间密度,一般以被选中的值为中心向两边拓展,并减小步长,同时范围可以向我们认为会被选中的一边倾斜。例如最大深度max_depth被选为14,我们则将原本的范围(2,30,2)修改为(10,25,1)。同样subsample被选为0.5,我们则将新范围调整为(0.3,0.7,0.05),依次类推。
step5:修改搜索空间
param_grid_simple = {'n_estimators': hp.quniform("n_estimators",100,180,5),"lr": hp.quniform("learning_rate",0.02,0.2,0.04),"criterion": hp.choice("criterion",["friedman_mse", "squared_error"]),"max_depth": hp.quniform("max_depth",10,25,1),"subsample": hp.quniform("subsample",0.3,0.7,0.05),"max_features": hp.quniform("max_features",10,20,1),"min_impurity_decrease":hp.quniform("min_impurity_decrease",0,5,0.5)}由于需要修改参数空间,因此目标函数也必须跟着修改:
def hyperopt_objective(params):reg = GBR(n_estimators = int(params["n_estimators"]),learning_rate = params["lr"],criterion = params["criterion"],max_depth = int(params["max_depth"]),max_features = int(params["max_features"]),subsample = params["subsample"],min_impurity_decrease = params["min_impurity_decrease"],loss = "squared_error",init = rf,random_state=1412,verbose=False) cv = KFold(n_splits=5,shuffle=True,random_state=1412)validation_loss = cross_validate(reg,X,y,scoring="neg_root_mean_squared_error",cv=cv,verbose=False,error_score='raise')return np.mean(abs(validation_loss["test_score"]))def param_hyperopt(max_evals=100): #保存迭代过程trials = Trials() #设置提前停止early_stop_fn = no_progress_loss(100) #定义代理模型params_best = fmin(hyperopt_objective, space = param_grid_simple, algo = tpe.suggest, max_evals = max_evals, verbose=True, trials = trials, early_stop_fn = early_stop_fn) #打印最优参数,fmin会自动打印最佳分数print("\n","\n","best params: ", params_best,"\n")return params_best, trialsparams_best, trials = param_hyperopt(30) #使用小于0.1%的空间进行训练100%|█████████████████████████████████████████████████| 30/30 [01:24<00:00, 2.82s/trial, best loss: 26673.75433067303]best params: {'criterion': 0, 'learning_rate': 0.04, 'max_depth': 12.0, 'max_features': 13.0, 'min_impurity_decrease': 3.5, 'n_estimators': 110.0, 'subsample': 0.7000000000000001}
params_best, trials = param_hyperopt(60) #尝试增加搜索次数100%|█████████████████████████████████████████████████| 60/60 [03:14<00:00, 3.24s/trial, best loss: 26736.01565552259]best params: {'criterion': 0, 'learning_rate': 0.08, 'max_depth': 13.0, 'max_features': 15.0, 'min_impurity_decrease': 1.0, 'n_estimators': 145.0, 'subsample': 0.7000000000000001}
基于该结果,我们又可以确定进一步确定部分参数的值(比如criterion),再次缩小参数范围、增加参数空间的密集程度。
step6:继续修改搜索空间
param_grid_simple = {'n_estimators': hp.quniform("n_estimators",100,150,1),"lr": hp.quniform("learning_rate",0.01,0.1,0.005),"max_depth": hp.quniform("max_depth",10,16,1),"subsample": hp.quniform("subsample",0.65,0.85,0.0025),"max_features": hp.quniform("max_features",12,16,1),"min_impurity_decrease":hp.quniform("min_impurity_decrease",1,4,0.25)}
def hyperopt_objective(params):reg = GBR(n_estimators = int(params["n_estimators"]),learning_rate = params["lr"],max_depth = int(params["max_depth"]),max_features = int(params["max_features"]),subsample = params["subsample"],min_impurity_decrease = params["min_impurity_decrease"],criterion = "friedman_mse",loss = "squared_error",init = rf,random_state=1412,verbose=False) cv = KFold(n_splits=5,shuffle=True,random_state=1412)validation_loss = cross_validate(reg,X,y,scoring="neg_root_mean_squared_error",cv=cv,verbose=False,error_score='raise')return np.mean(abs(validation_loss["test_score"]))def param_hyperopt(max_evals=100): #保存迭代过程trials = Trials() #设置提前停止early_stop_fn = no_progress_loss(100) #定义代理模型params_best = fmin(hyperopt_objective, space = param_grid_simple, algo = tpe.suggest, max_evals = max_evals, verbose=True, trials = trials, early_stop_fn = early_stop_fn) #打印最优参数,fmin会自动打印最佳分数print("\n","\n","best params: ", params_best,"\n")return params_best, trialsparams_best, trials = param_hyperopt(300) #缩小参数空间的同时增加迭代次数43%|███████████████████▉ | 130/300 [06:12<08:06, 2.86s/trial, best loss: 26563.111168263265]best params: {'learning_rate': 0.055, 'max_depth': 10.0, 'max_features': 13.0, 'min_impurity_decrease': 1.25, 'n_estimators': 124.0, 'subsample': 0.7675000000000001}
关闭提前停止,继续迭代:
def param_hyperopt(max_evals=100): #保存迭代过程trials = Trials()#定义代理模型params_best = fmin(hyperopt_objective, space = param_grid_simple, algo = tpe.suggest, max_evals = max_evals, verbose=True, trials = trials) #打印最优参数,fmin会自动打印最佳分数print("\n","\n","best params: ", params_best,"\n")return params_best, trialsparams_best, trials = param_hyperopt(300) #取消提前停止,继续迭代100%|███████████████████████████████████████████████| 300/300 [13:52<00:00, 2.77s/trial, best loss: 26412.12758959595]best params: {'learning_rate': 0.085, 'max_depth': 10.0, 'max_features': 13.0, 'min_impurity_decrease': 2.75, 'n_estimators': 145.0, 'subsample': 0.675}
start = time.time()
hyperopt_validation({'criterion': "friedman_mse",'learning_rate': 0.085,'loss': "squared_error",'max_depth': 10.0,'max_features': 13,'min_impurity_decrease': 2.75,'n_estimators': 145.0,'subsample': 0.675})26412.12758959595
end = (time.time() - start)
print(end)2.7066071033477783
| 算法 | RF | AdaBoost | GBDT | RF (TPE) | AdaBoost (TPE) | GBDT (TPE) |
|---|---|---|---|---|---|---|
| 5折验证 运行时间 | 5.35s | 0.99s | 2.16s | 1.36s | 0.83s | 2.70s(↑) |
| 最优分数 (RMSE) | 30571.267 | 35345.931 | 28783.954 | 28346.673 | 35169.73 | 26412.1278(↓) |
GBDT获得了目前为止的最高分,虽然这一组参数最终指向了145棵树,导致GBDT运行所需的时间远远高于其他算法,GBDT上得到的分数是比精细调参后的随机森林还低2000左右,这证明了GBDT在学习能力上的优越性。由于TPE是带有强随机性的过程,因此如果我们多次运行,我们将得到不同的结果,但GBDT的预测分数可以稳定在26500上下。如果算力支持使用更多的迭代次数、或使用更大更密集的参数空间,我们或许可以得到更好的分数。同时,如果能够找到一组大学习率、小迭代次数的参数,那GBDT的训练速度也会随之上升。
相关文章:

GBDT的参数空间与超参数优化
目录 1. 默认参数下的GBDT与其它算法的对比 2. 基于TPE对GBDT进行优化 step1:建立benchmark step2:定义参数init需要的算法 step3:定义目标函数、参数空间、优化函数、验证函数 step4:训练贝叶斯优化器 step5:修…...

多线程练习——抽奖箱
题目: 分析以下需求,并用代码实现: 有一个抽奖池,该抽奖池中存放了奖励的金额,该抽奖池中的奖项为 {10,5,20,50,100,200,500,800,900,2,80,300,700};创建两个抽奖箱(线程)设置线程名称分别为“抽奖箱1”,“抽奖箱2”,随…...

RK3399平台开发系列讲解(内核调试篇)Valgrind 内存调试与性能分析
🚀返回专栏总目录 文章目录 一、为什么要学会Valgrind二、什么是内存泄露三、Valgrind的移植四、Valgrind相关参数沉淀、分享、成长,让自己和他人都能有所收获!😄 📢Valgrind 是一个开源的内存调试和性能分析工具,用于帮助开发者找出程序中的内存错误,如内存泄漏、使…...
Windows 11的最新人工智能应用Windows Copilot面世!
Windows Copilot是Windows 11预览版中的一项AI辅助功能。 Windows 11还包括设置应用程序的更改,更广泛的支持压缩文件格式。 上个月,微软宣布将继续其将ChatGPT应用于所有产品的冒险之旅,推出了名为Copilot的新Windows 11功能。几个月前&…...
Mac 预览(Preview)丢失PDF标注恢复
感谢https://blog.csdn.net/yaoyao_chen/article/details/127462497的推荐! 辛苦用预览在pdf上做的阅读标记,关闭后打开全丢失了,推荐尝试下网站导入文件进行恢复: 直接使用该网页应用PDF Annotation Recovery 或者访问该项目&a…...

4.5. 方法的四种类型
文章目录 1、无参数无返回值的方法2、有参数无返回值的方法3、有返回值无参数的方法4、有返回值有参数的方法5、return 在无返回值方法的特殊使用 1、无参数无返回值的方法 // 无参数无返回值的方法(如果方法没有返回值,不能不写,必须写void,…...

四旋翼无人机使用教程
文章目录 前言一、检查遥控器电源开关混控拨码开关微调开关飞行模式刹车开关行程开关接收机对码 二、检查飞机检查接线 三、解锁并飞行 前言 PX4固件 QGC地面站 Pixhwak飞控 Mc6c遥控器 开源飞控博大精深,欢迎广大爱好者加博主微信名片,一起学习交流。…...

优化 PHP 数据库查询性能
优化 PHP 数据库查询性能可以从以下几个方面入手: 使用索引:在数据库中创建适当的索引可以大大提高查询性能。索引可以加快数据的查找速度,特别是在大型数据库中。选择合适的数据类型:选择正确的数据类型可以减少存储空间的占用&…...

vue 使用stompjs websocket连接rabbitmq
1. 首先确保rabbitmq服务已开启web-stomp 1.1 登录rabbitmq web控制台 1.2 在overview目录下 下拉找到Ports and contexts 看列表有没有http/web-stomp 1.3 如果没有需要开启 window/centos 进入rabbitmq安装目录的bin目录下执行rabbitmq-plugins enable rabbitmq_web_stomp ra…...
com.android.ide.common.signing.KeytoolException:
签名没问题但是提示Execution failed for task :app:packageDebug. > A failure occurred while executing com.android.build.gradle.tasks.PackageAndroidArtifact$IncrementalSplitterRunnable > com.android.ide.common.signing.KeytoolException: Failed to read ke…...
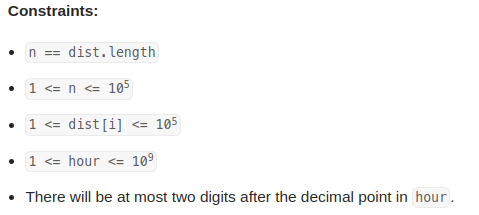
leetcode 1870. Minimum Speed to Arrive on Time(准时到达的最小速度)
需要找一个speed, 使得dist[i] / speed 加起来的时间 < hour, 而且如果前一个dist[i] / speed求出来的是小数,必须等到下一个整数时间才计算下一个。 speed最大不会超过107. 不存在speed满足条件时返回-1. 思路: 如果前一个dist[i] / speed求出来的…...

本地非文字资源无法加载
目录 方法A.静态/动态绑定路径 方法B.require导入(运行时加载) 方法C.import导入(x)(编译时加载) 方法D.ref直接操作元素赋值(x) 相关知识 import和requir区别 模板路径&#…...

Java电子招投标采购系统源码-适合于招标代理、政府采购、企业采购
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查看…...
万向节死锁
要理解万向节死锁的产生原因,首先要理解欧拉角变换,欧拉角变换是基于最初始的坐标进行变换而非变换后的坐标进行变换。 欧拉角变换需要空间中的三个角(即变换后每个轴的偏移量),另外还有每个轴的变换顺序。值得注意的…...

大数据课程D1——hadoop的初识
文章作者邮箱:yugongshiyesina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解大数据的概念; ⚪ 了解大数据的部门结构; ⚪ 了解hadoop的定义; ⚪ 了解hadoop的发展史; 一、大数据简介 1. 概述…...

xml命名空间
xml命名空间 一个xml文档中可以包含多个元素和属性,在文档中使用多个DTD文件时,可能会碰到相同的元素,而这些名称相同的元素可能代表了完全不同的含义,为了防止命名冲突,W3C提供了一个推荐标准-XML命名空间 命名空间有…...
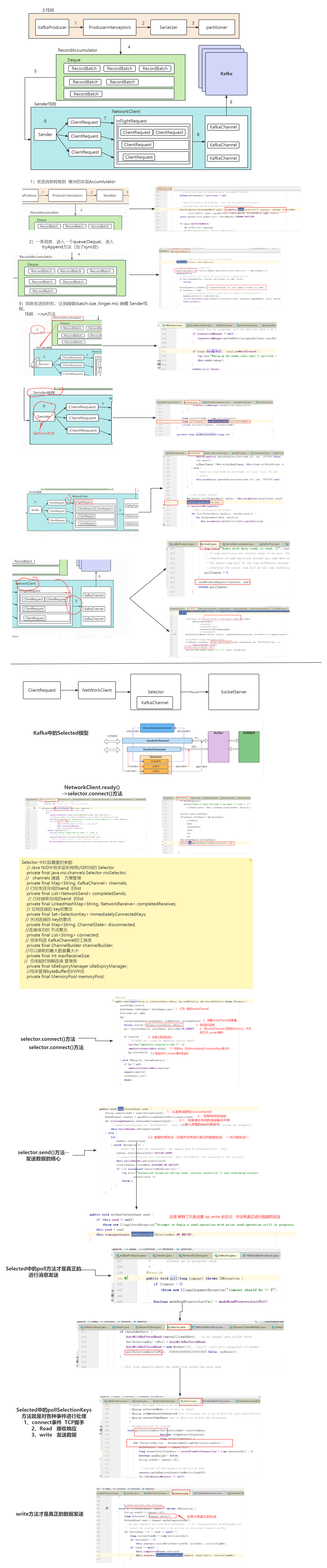
七、Kafka源码分析之网络通信
1、生产者网络设计 架构设计图 2、生产者消息缓存机制 1、RecordAccumulator 将消息缓存到RecordAccumulator收集器中, 最后判断是否要发送。这个加入消息收集器,首先得从 Deque 里找到自己的目标分区,如果没有就新建一个批量消息 Deque 加进入 2、消…...
WEB安全测试通常要考虑的测试点
1、问题:没有被验证的输入 测试方法: 数据类型(字符串,整型,实数,等) 允许的字符集 最小和最大的长度 是否允许空输入 参数是否是必须的 重复是否允许 数值范围 特定的值(枚举型&a…...
的duration音频长度获取不到问题)
关于uni.createInnerAudioContext()的duration音频长度获取不到问题
关于uni.createInnerAudioContext()的duration音频长度获取不到问题 代码如下: onLoad() {let _this this//初始化语音播放对象this.audioObj uni.createInnerAudioContext();this.audioObj.src 音频链接;// 音频进入可以播放状态,但不保证后面可以流…...

使用rknn-toolkit2把YOLOV5部署到OK3588上
使用rknn-toolkit2把YOLOV5部署到OK3588上 虚拟环境搭建软件包安装在PC机上运行yolov5目标检测 虚拟环境搭建 首先在PC的ubuntu系统安装虚拟环境: 我的服务器是ubuntu18.04版本,所以安装python3.6 conda create -n ok3588 python3.6 需要键盘输入y&…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
