【SDOF振荡器的非线性-非弹性多轴时间响应分析】用于SDOF振荡器非线性非弹性时程分析的鲁棒性分析研究(Matlab代码实现)
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
进行SDOF振荡器的非线性非弹性时程分析的鲁棒性分析研究,旨在探究该方法对不同系统参数和分析条件变化的稳定性和可靠性。以下是一些可能的研究内容和方法:
1. 参数变化对结果的影响:通过对系统参数进行变化,例如刚度、阻尼、质量等,观察这些参数变化对非线性非弹性时程分析结果的影响。可以分析参数变化对振动响应的幅值、频谱特性、时程历程等的影响,进而评估该方法的稳定性和准确性。
2. 非线性模型的复杂度:考虑不同程度的非线性,比如线性衰减、非线性阻尼、非线性刚度等,并对这些模型进行时程分析。通过对比不同非线性程度下的振动响应结果,评估方法对于复杂非线性模型的鲁棒性。
3. 非线性耦合效应:对于涉及多个非线性项的情况,如非线性刚度和非线性阻尼同时存在的振动系统,研究该方法对于非线性耦合效应的处理能力。通过引入不同程度的耦合效应,分析其对时程分析结果的影响,进而评估方法的鲁棒性。
4. 数值方法的稳定性:对于非线性非弹性时程分析方法使用的数值方法,如数值积分算法,进行稳定性研究。通过修改数值方法的步长、积分算法等参数,观察这些参数变化对求解结果的影响,评估方法的稳定性和可靠性。
5. 算法对比分析:将SDOF振荡器的非线性非弹性时程分析方法与其他数值方法进行对比,例如频域方法、步进法等,比较它们的优劣和鲁棒性。可以选取不同的振动系统和不同的分析条件,通过对比结果的准确性和收敛性来评估方法的鲁棒性。
通过以上鲁棒性分析研究,可以对SDOF振荡器的非线性非弹性时程分析方法在不同情况下的适用性和可靠性进行评估,提供工程实际应用的指导和建议。
强大的 MatLAB 功能,用于对 SDOF 振荡器进行非线性非弹性时程分析,该振荡器承受多轴同时激励,包括水平、垂直和旋转运动。它还计算传递给SDOF振荡器的地震输入能量的分量。
主要特点是:- 多轴激励 - 材料非线性由Ozdemir的速率无关力-位移模型
表示 - 包括
P-Delta(全局水平)
- 绝对和相对能量分量计算
📚2 运行结果

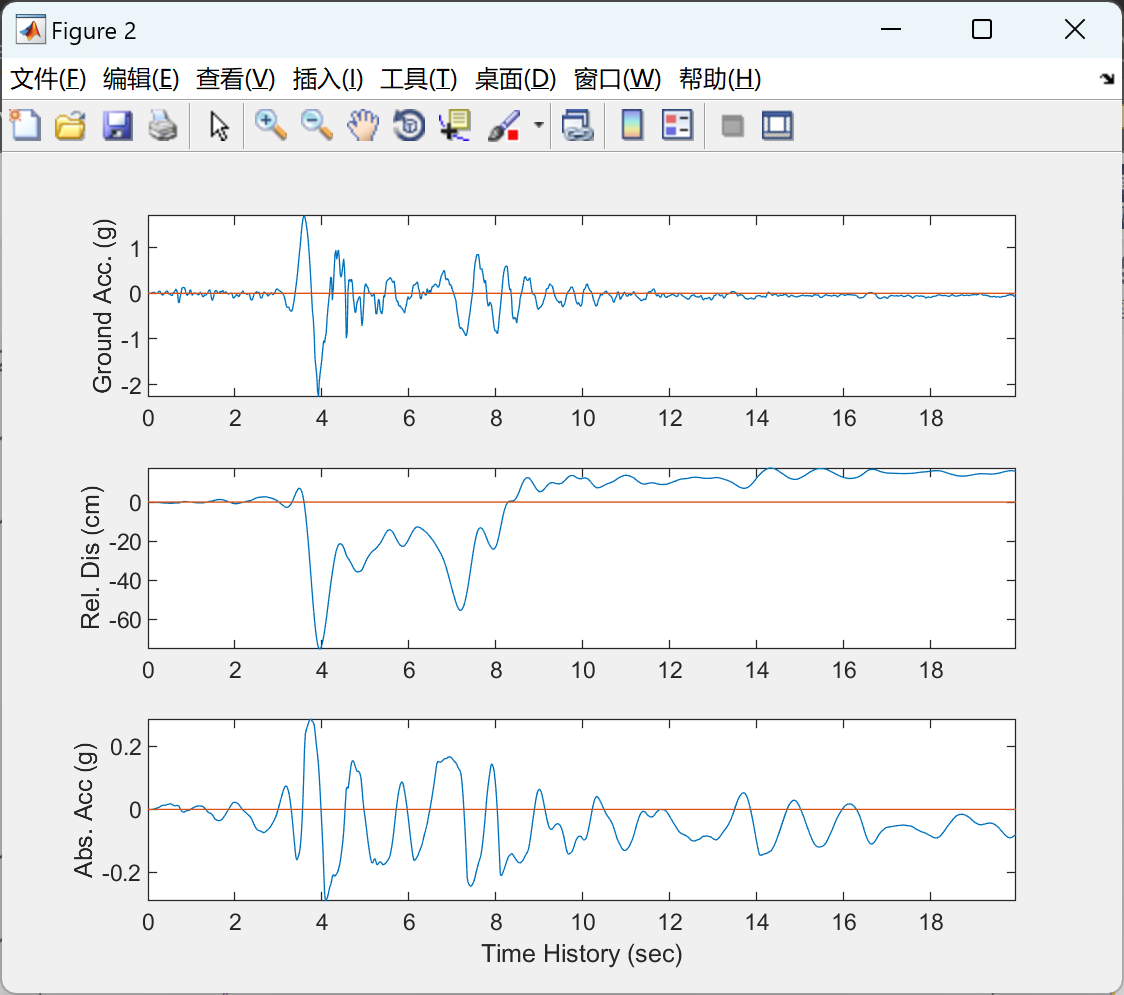
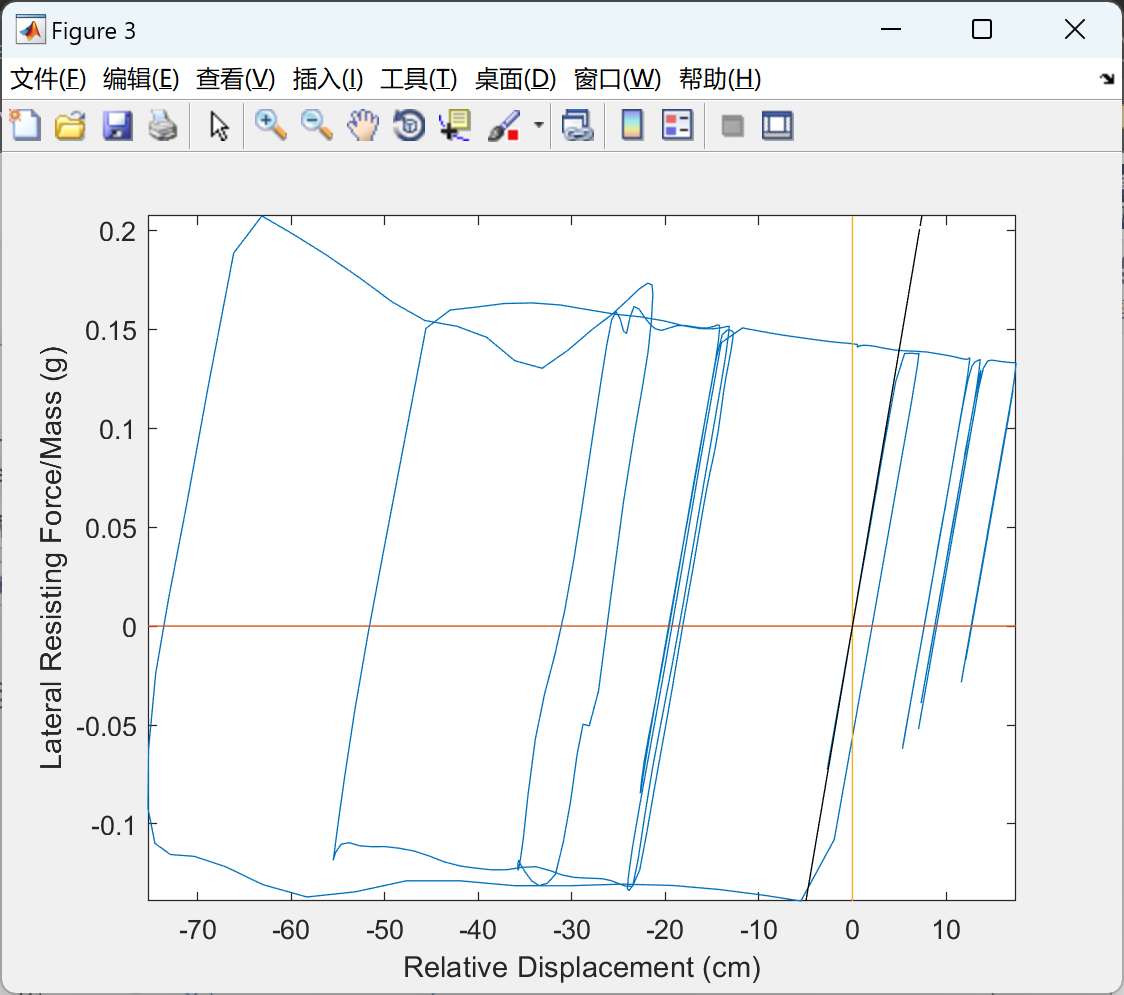
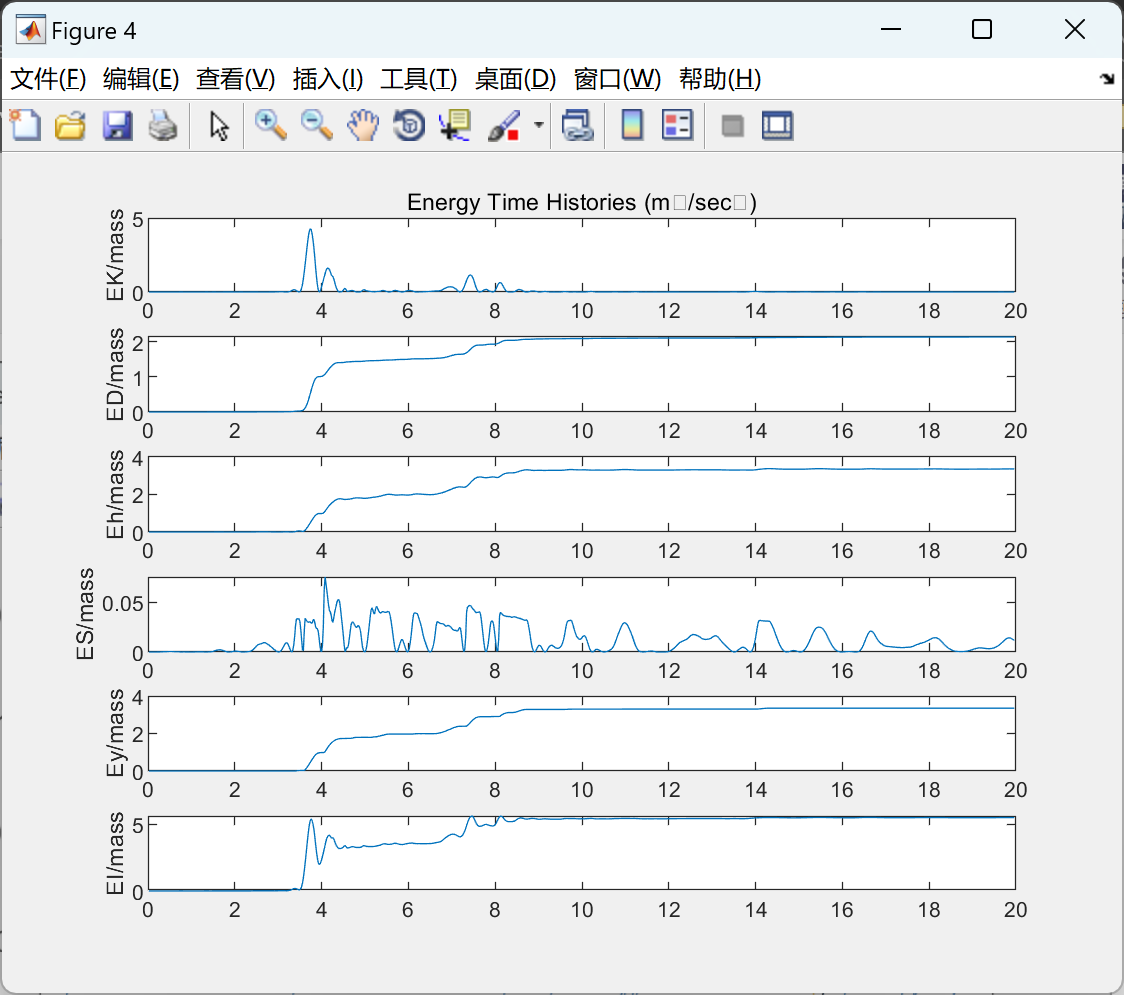

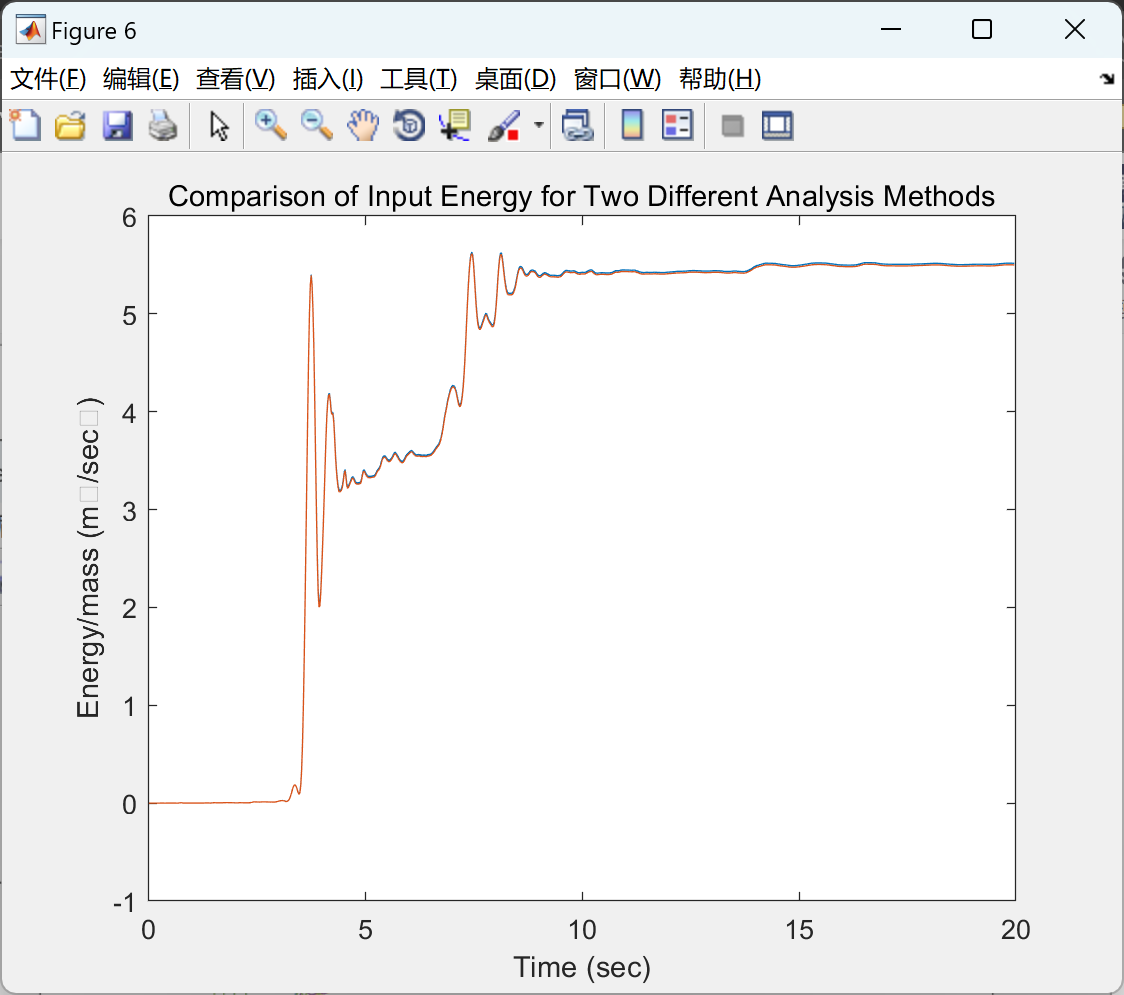
部分代码:
Tn = 1.2; % Natural period (sec)
omegan = 2*pi/Tn; % Natural frequency (rad/sec)
xi = 0.05; % Damping ratio
g = 9.81; % Gravity constant (m/sec�)
%fy = 0.2533*g; % Yield force (normalized by mass which is already 1.0)
ky = 2.40;
%uy = ky/omegan^2; % Yield displacement (m)
uy = 0.0523
alpha = 0.02; % Post to pre-yielding stiffness ratio
eta = 21; % Elastic to inelastic transition parameter
l = 9; % Length of oscillator (m) (if it is too large, small geometric stiffness term)
Kg = g/l; % Geometric stiffness term (1/sec�)
Tg = 2*pi*(1/Kg)^.5; % Static geometric oscillation period (sec) see ASCE paper by Kalkan & Graizer (2007)
dt = 0.02; % Time step of ground acceleration (sec)
[gacc gaccZ gaccH term3 term4] = groundMotionData(l,g,dt); % Call ground motion input data function
% Assign values to integration variables
N = length(gacc); % Number of points
td = N*dt; % Duration of ground motion
tspan = (dt:dt:td); % Time vector (sec)
y1o = 0; % Initial value of y1
y2o = 0; % Initial value of y2
y3o = 0; % Initial value of y3
y4o = 0; % Initial value of y4
y5o = 0; % Initial value of y5
yo = [y1o;y2o;y3o;y4o;y5o]; % Initial conditions for state vector
% Call ODE solver to solve system of first-order ODE's
% (Use a stiff solver since the euqations are nonlinear)
[t,y] = ode15s('nonlinsysMultiAxial',tspan,yo,[],omegan,xi,gacc,tspan,uy,alpha,eta,td,Kg,gaccZ,l,dt);
% Extract response from state vector
% (Note that the output of the ODE solver is the state vector y)
% in which yi as a function of time is in the i-th column
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Dr. Erol Kalkan, P.E. (2023). NONLINEAR-INELASTIC MULTI-AXIAL TIME RESPONSE ANALYSIS OF SDOF OSCILLATOR.
[2]Yaghmaei-Sabegh S,Daneshgari S.Effect of ground motion duration on inelastic displacement ratio of SDOF systems[J].Earthquake Engineering and Engineering Vibration,2023,22(02):423-439.
[3]侯红梅,刘文锋,张怀超.基于SDOF体系和高层结构的地震动强度指标研究[J].地震工程学报,2021,43(06):1436-1443.
🌈4 Matlab代码实现
相关文章:

【SDOF振荡器的非线性-非弹性多轴时间响应分析】用于SDOF振荡器非线性非弹性时程分析的鲁棒性分析研究(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 🌈4 Matlab代码实现 💥1 概述 进行SDOF振荡器的非线性非弹性时程分析的鲁棒性分析研究,旨在探究该方法对不同系统参数和分析条件变化的稳定性和可靠性。以下是一…...

VMPWN的入门系列-1
5.1 实验一 VMPWN1 5.1.1 题目简介 这是一道基础的VM相关题目,VMPWN的入门级别题目。前面提到VMPWN一般都是接收字节码然后对字节码进行解析,但是这道题目不接受字节码,它接收字节码的更高一级语言:汇编。程序直接接收类似”mov…...

将标签中某一个类别添加到另一个标签中
现在有两张CItyscapes数据集的标签,假设我想把第二张图骑车的人添加到第一张图,暂且不考虑添加位置的变换,那么该如何操作呢? 1:将骑车的人和车作为两个类别独立于其他的类别出来。 2:将这两个类别作为一个…...

将指定图片控件中的图片闪烁
/// <summary> /// 将指定图片控件中的图片闪烁 /// </summary> /// <param name"pic">需要闪烁的图片控件</param> public static void FlashImage(object picBox) { try …...
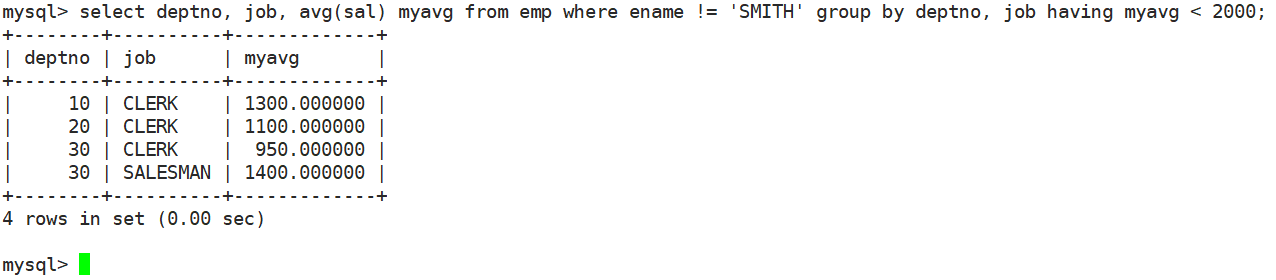
【MySQL】表的增删查改
目录 一、Create创建 1、单行数据全列插入 2、多行数据指定列插入 3、插入更新 4、替换 二、Retrieve查询 1、SELECT 列 1.1、 全列查询 1.2、指定列查询 1.3、查询字段为表达式 1.4、结果去重 2、where条件 2.1、英语不及格的同学及英语成绩 ( < 60 ) 2.2、语…...
Python 爬虫的学习 day01 ,爬虫的基本知识, requests 和 charde模块, get函数的使用
1.Python 爬虫 1.1什么是网络爬虫 网络爬虫,又称为网页蜘蛛,网络机器人,是一种按照一定的规则,自动地抓取万维网信息的程序或者脚本,另外一些不常使用的名字还有蚂蚁、自动索引、模拟程序或者蠕虫。 1.2 网络爬虫的特…...
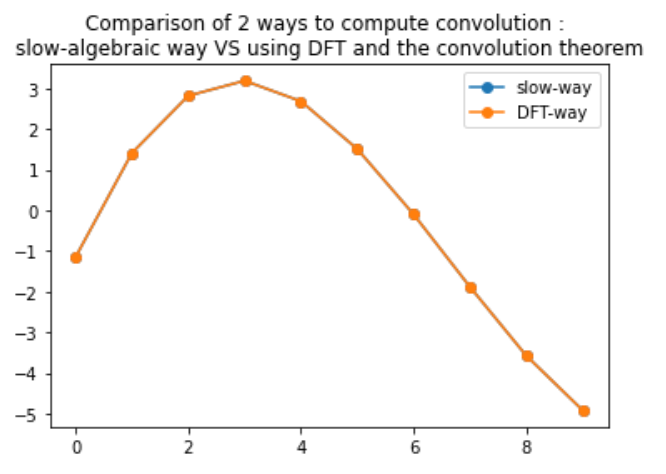
【数据挖掘】时间序列的傅里叶变换:用numpy解释的快速卷积
一、说明 本篇告诉大家一个高级数学模型,即傅里叶模型的使用; 当今,傅里叶变换及其所有变体构成了我们现代世界的基础,为压缩、通信、图像处理等技术提供了动力。我们从根源上理解,从根本上应用,这是值得付…...
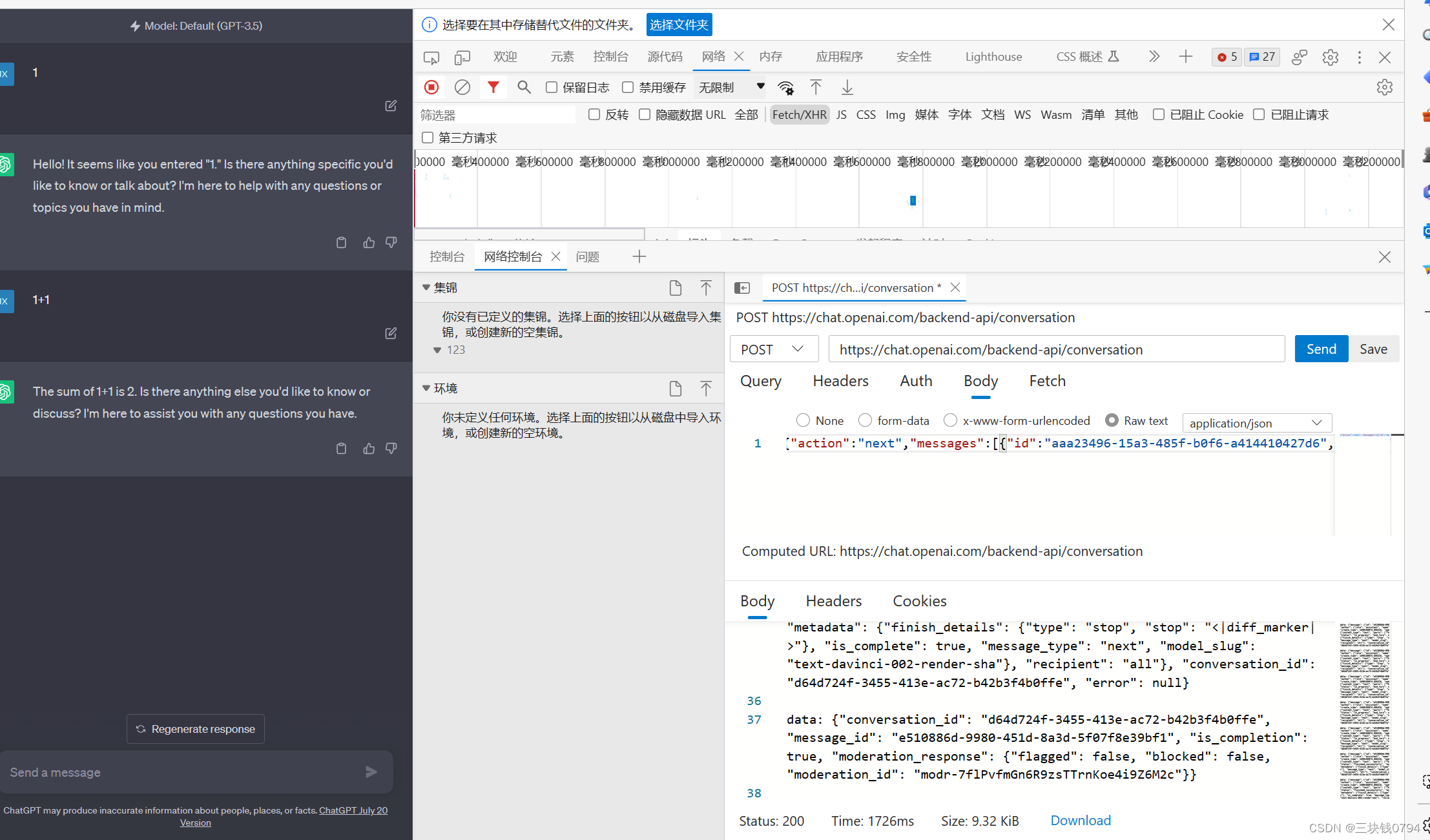
Chatgpt Web API 创建对话,免费,不计token数量,模仿网页提交对话
Chatgpt API 是收费的,按token使用量计费 Chatgpt Web API 免费的,只要有账号就可以使用。 curl https://chat.openai.com/backend-api/conversation \-H authority: chat.openai.com \-H accept: text/event-stream \-H accept-language: zh-CN,zh;q…...
嵌入式软件—RK3568开发环境搭建
一、RK3568 1.1 开发板特点 BSP比较大,对于电脑内存和存储空间要求高 1.2 BSP BSP(Board Support Package,板级支持包),类似于PC系统中BIOS和驱动程序的集合,BSP包含的范围更广,除了外设驱动…...

使用 OpenCV 和 GrabCut 算法进行交互式背景去除
一、说明 我想,任何人都可以尝试从图像中删除背景。当然,有大量可用的软件或工具能够做到这一点,但其中一些可能很昂贵。但是,我知道有人使用窗口绘画3D魔术选择或PowerPoint背景去除来删除背景。 如果您是计算机视觉领域的初学者…...

在Windows server 2012上使用virtualBox运行CentOS7虚拟机,被强制休眠(二)
问题场景 本月7月10日处理了一个虚拟机被强制暂停的问题,详见:在Windows server 2012上使用virtualBox运行CentOS7虚拟机,被强制暂停当时是由于C盘存储空间不足,导致虚拟机被强制暂停,将虚拟机迁移后,问题…...
sql学习笔记
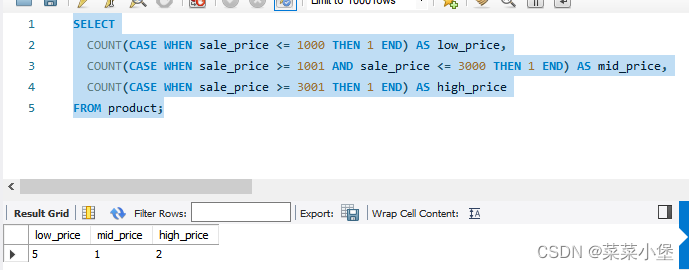
sql语句优先级 FROM → WHERE → GROUP BY → SELECT → HAVING → ORDER BY sql case用法 例题: 按照销售单价( sale_price )对练习 3.6 中的 product(商品)表中的商品进行如下分类。 低档商品:销售单价在1000日元以下&#x…...

Ubuntu 20.04.4 LTS安装Terminator终端(Linux系统推荐)
Terminator终端可以在一个窗口中创建多个终端,并且可以水平、垂直分割,运行ROS时很方便。 sudo apt install terminator这样安装完成后,使用快捷键Ctrl Alt T打开的就是新安装的terminator终端,可以使用以下方法仍然打开ubuntu默…...

22. 括号生成
题目描述 数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 示例 1: 输入:n 3 输出:["((()))","(()())","(())()","()(())",&…...

WPF实战学习笔记05-首页界面
首页界面 新建文件 添加文件[类型:用户控件] ./Common/Models/TaskBars.cs ./Common/Models/ToDoDto.cs ./Common/Models/MemoDto.cs 新建类 TaskBars.cs using System; using System.Collections.Generic; using System.Linq; using Sy…...
一文带你迅速入门SprIngMVC,看这一篇就足够了!
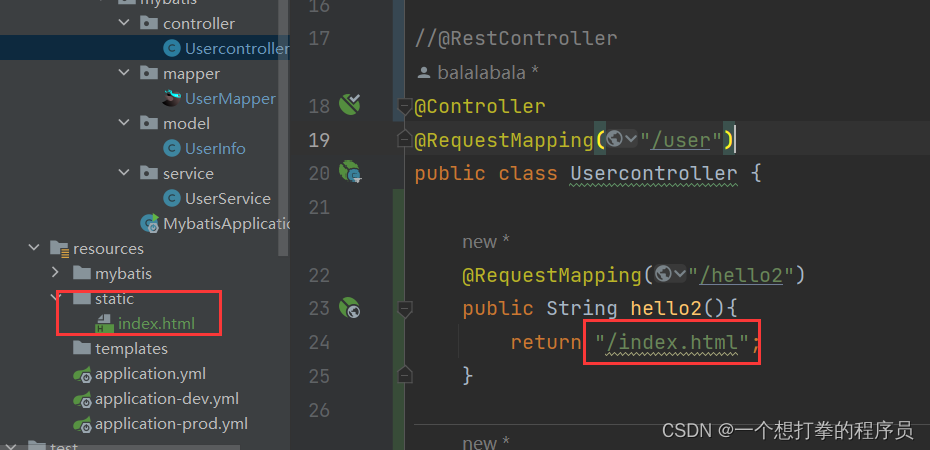
0. 什么是SpringMVC 要知道什么是SpringMVC,我们首先得知道什么 MVC,MVC是软件工程中的一种架构模式,分为 Model、View、Control。它把软件系统分为模型、视图和控制器三个基本部分。 Model:模型,应用程序负责数据逻…...

js路由跳转时放弃正在pending的请求
在单页面应用中通常会对请求进行catch处理,如果用户打开a页面后页面发出了一个请求去获取aaa,但是由于某种原因请求一直在pending。此时用户又进入了b页面,在浏览时a页面的请求失败了,然后页面弹出提示:“数据aaa请求失…...
-0723)
LeetCode(sql)-0723
聚合函数 620 select * from cinema where mod(id,2)1 and description <> boring order by rating desc1251 select p.product_id, Round(sum(price*units)/sum(units),2)as average_price from UnitsSold u left join Prices p using(product_id) where purchase_d…...

【C++】开源:grpc远程过程调用(RPC)配置与使用
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍grpc远程过程调用(RPC)配置与使用。 无专精则不能成,无涉猎则不能通。。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜…...
rabbitmq模块启动报java.net.SocketException: socket closed的解决方法
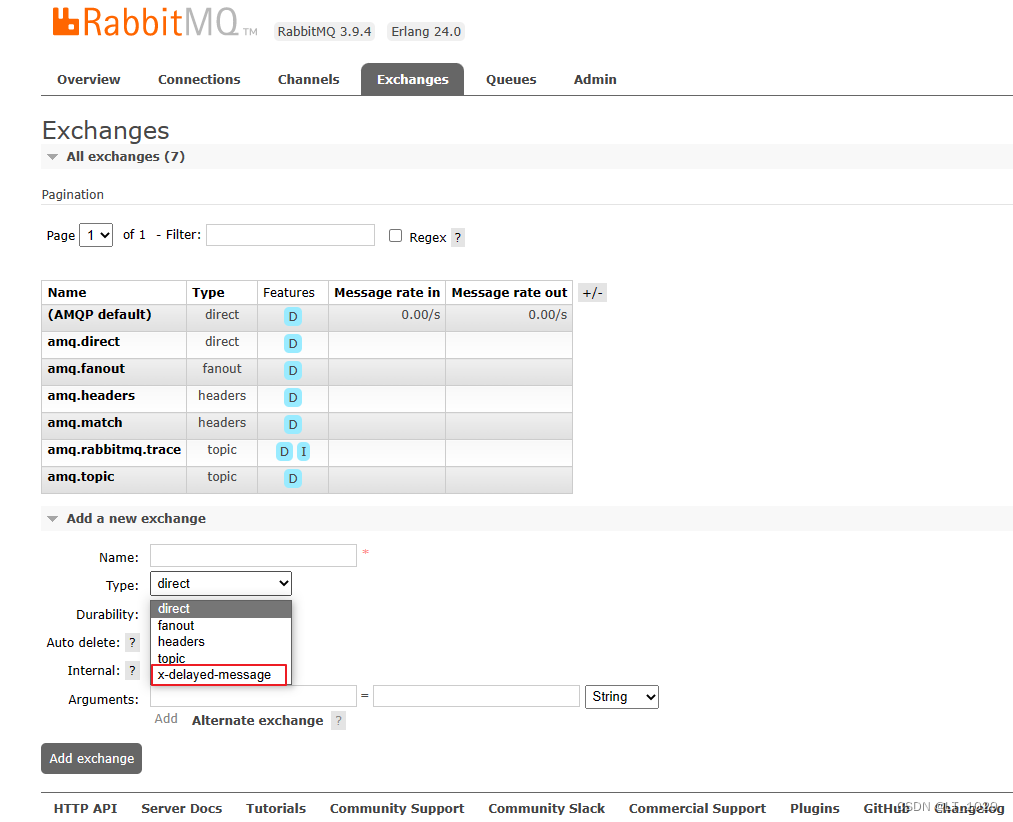
问题 最近在接手一个项目时,使用的是spring-cloud微服务构架,mq消息消费模块是单独一个模块,但启动这个模块一直报如下错误: java.net.SocketException: socket closed 这个错误是这个模块注册不到nacos报的错,刚开…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

