服务器 Docker Alist挂载到本地磁盘(Mac版)夸克网盘
1.服务器下载alist
默认有docker环境
docker pull xhofe/alist
2.生成容器
-v /home/alist:/opt/alist/data
这段意思是alist中的数据映射到docker 主机的文件夹,/home/alist就是我主机的文件夹,这个文件夹必须先创建
docker run -d --restart=always -v /home/alist:/opt/alist/data -p 5244:5244 -e PUID=0 -e PGID=0 -e UMASK=022 --name="alist" xhofe/alist:latest
3.开通服务器的5244访问

4.获得Alist初始登录密码
docker exec -it alist ./alist admin
5.登录web服务器,输入账号密码
http://ip:5244
6.配置夸克服务器
- 点击最下方的管理
- 点击-存储-添加
- 选择夸克驱动,也可以是其他网盘
https://alist.nn.ci/zh/guide/#support-storage 这个地址里面有所有支持网盘的设置,这里我只演示下夸克网盘
就几个地方需要填写
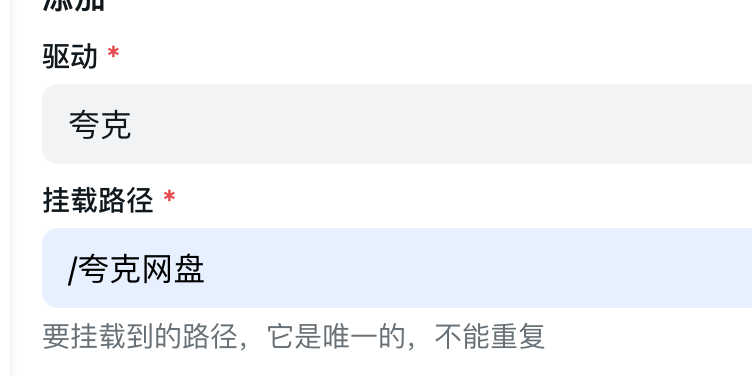
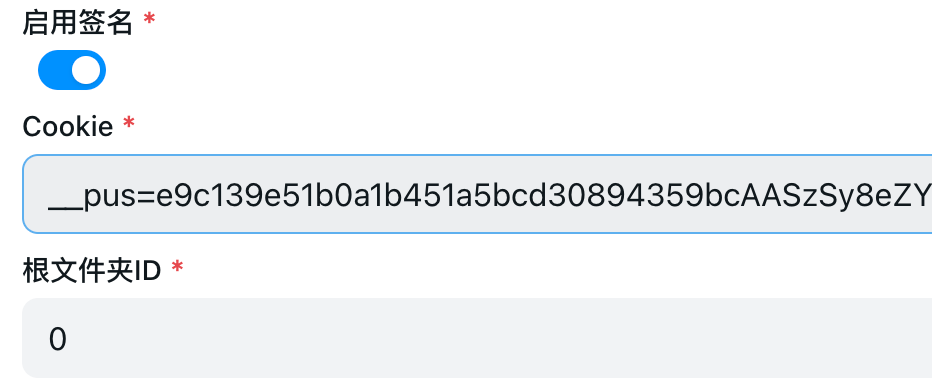
除了cookie之外都照着填就可以,现在讲一下夸克的cookie的获取
首先登录网页版本夸克:地址 https://pan.quark.cn/
按F12 点击网络/NetWork 右键页面刷新,然后找到请求中的sort开头的请求,然后在标投中找到cooki复制
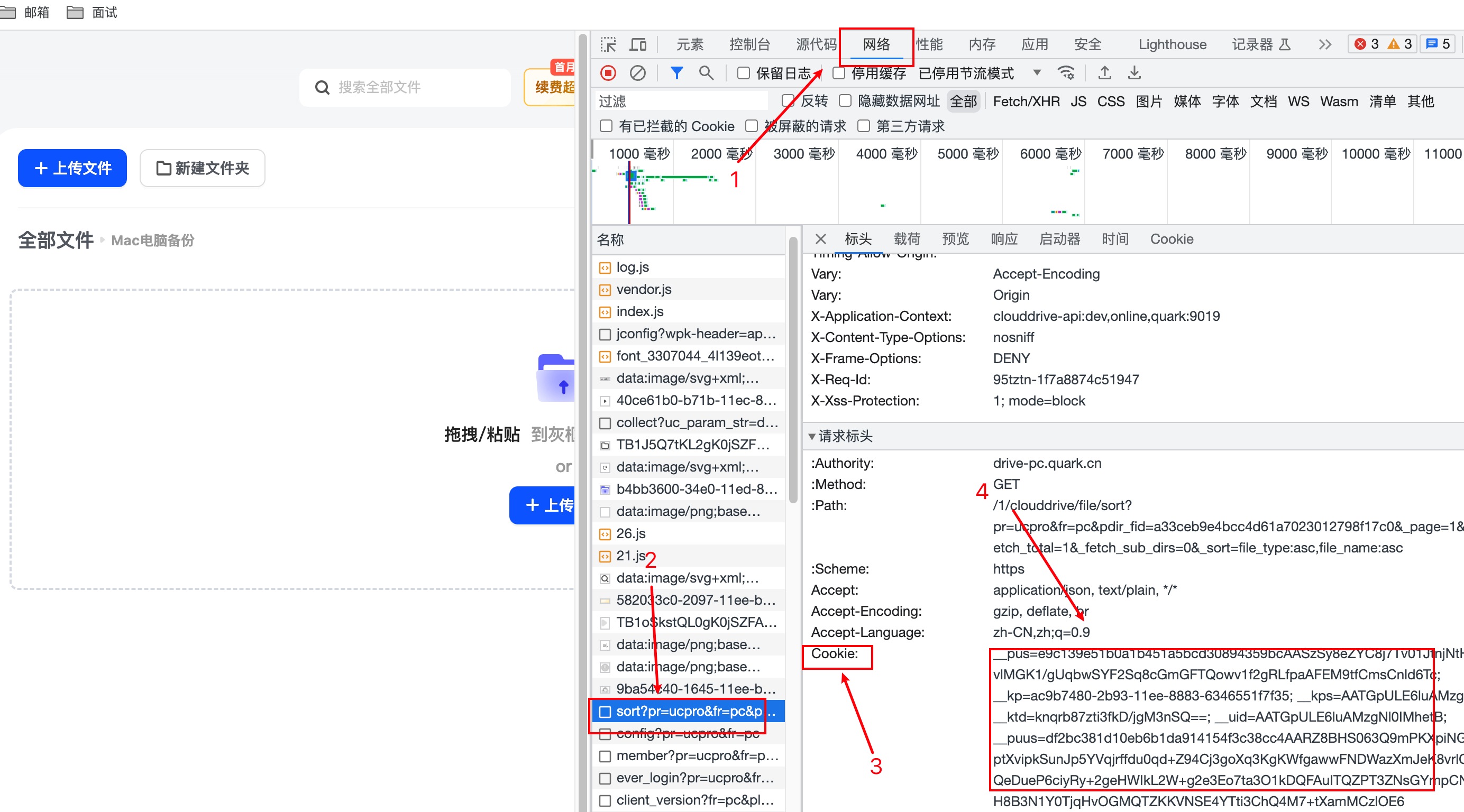
然后点击左下角的主页就看到我们的网盘啦,刚开始的话会同步一会,没有内容是正常的。
7.挂在服务器到本地
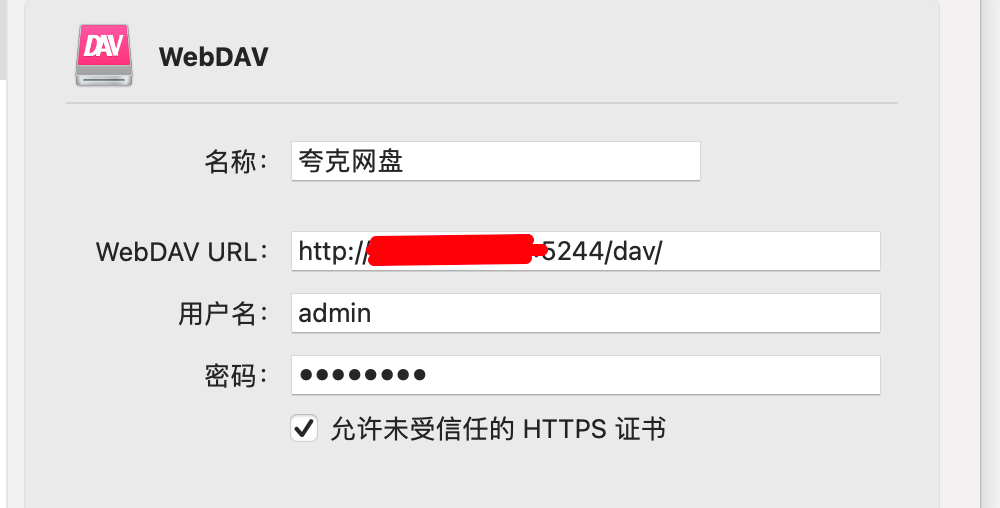
我电脑是mac,所以使用的是CloundMounter这个软件,如果你是windows的话可以使用其他的挂在软件,CloundMounter这个软件目前在appStore就可以下载
http://ip:5244/dav/ 一定到要在末尾加上/dav/不然不会成功
可以看到本地已经有挂载的网盘啦
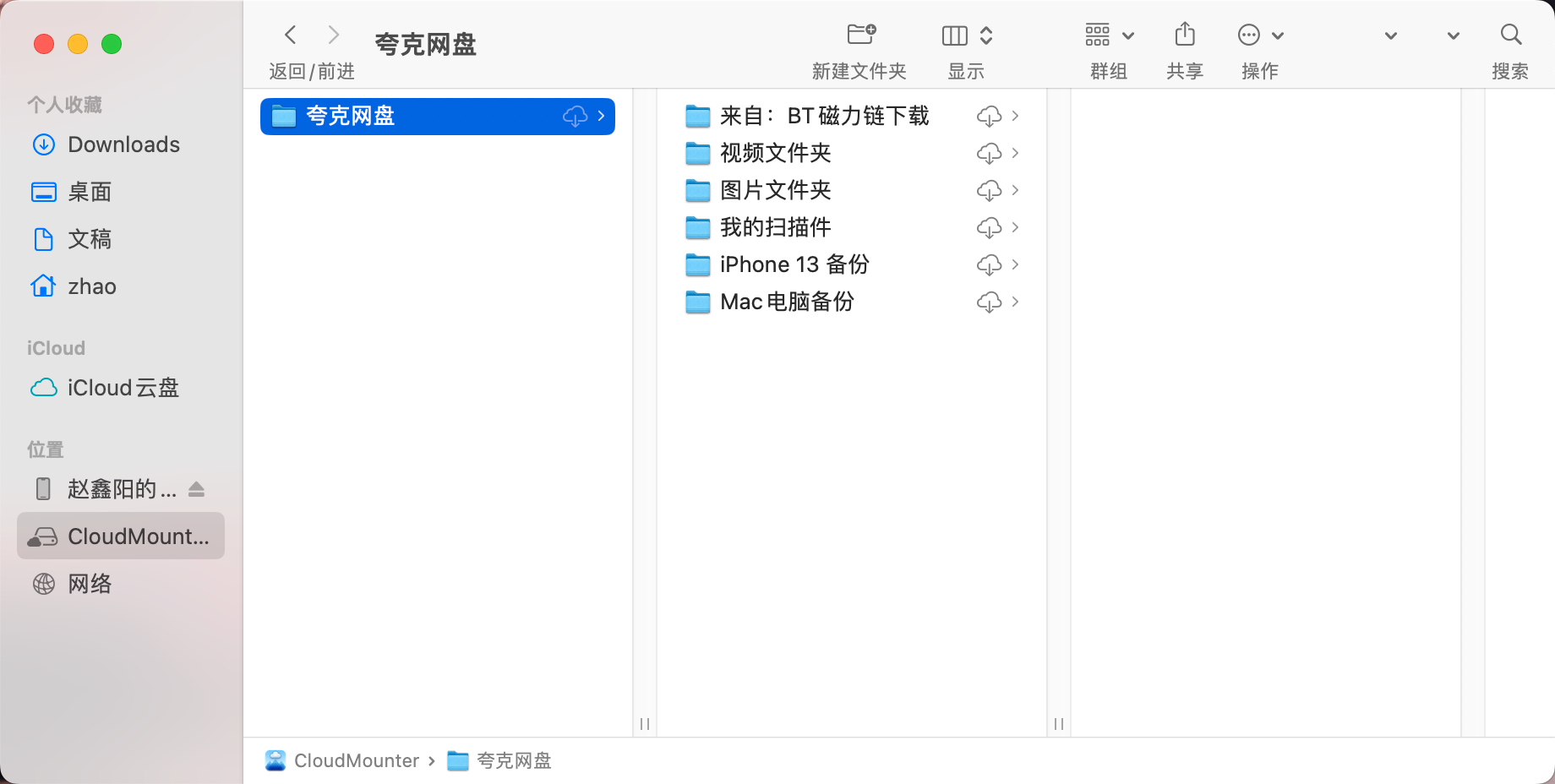
如过没有服务器的话,想在本地安装alist可以看这篇文章
https://zhuanlan.zhihu.com/p/612368639
相关文章:

服务器 Docker Alist挂载到本地磁盘(Mac版)夸克网盘
1.服务器下载alist 默认有docker环境 docker pull xhofe/alist2.生成容器 -v /home/alist:/opt/alist/data 这段意思是alist中的数据映射到docker 主机的文件夹,/home/alist就是我主机的文件夹,这个文件夹必须先创建 docker run -d --restartalways…...
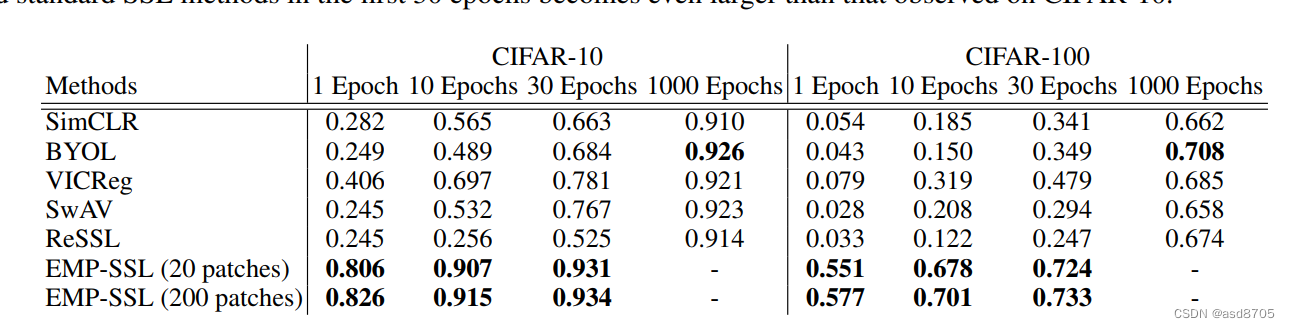
EMP-SSL: TOWARDS SELF-SUPERVISED LEARNING IN ONETRAINING EPOCH
Recently, self-supervised learning (SSL) has achieved tremendous success in learning image representation. Despite the empirical success, most self-supervised learning methods are rather “inefficient” learners, typically taking hundreds of training epoch…...
注解和反射01--什么是注解
注解 什么是注解内置注解元注解自定义注解 什么是注解 1、注解是从JDK5.0开始引入的新技术 2、注解的作用 (1)不是程序本身,可以对程序做出解释(和注释相同) (2)可以被其他程序读取,…...
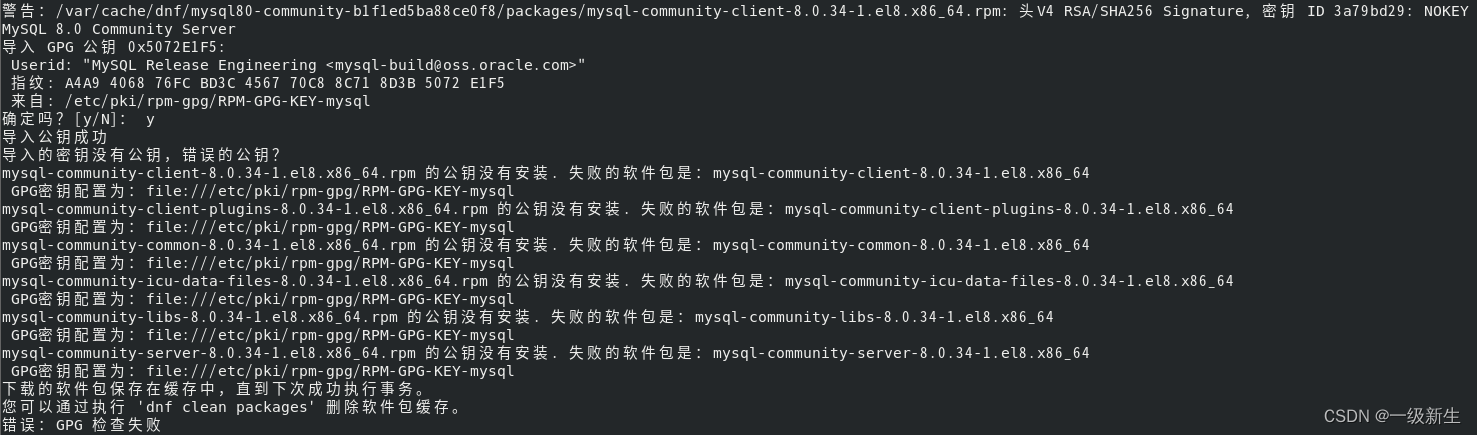
虚拟机 RHEL8 安装 MySQL 8.0.34
目录 安装步骤一、清除所有残留的旧MySQL二、安装MySQL 报错问题1. 提示未找到匹配的参数: mysql-community-server2. 公钥问题 安装步骤 一、清除所有残留的旧MySQL 1. 关闭MySQL [rootlocalhost /]# service mysqld stop Redirecting to /bin/systemctl stop …...

kafka 总结宝典
...
跨平台力量:探索C++Qt框架的未来前景
卓越的跨平台支持:CQt可以在多个平台上运行,包括Windows、Mac、Linux、Android和iOS等。这使得开发者能够使用同一份代码构建跨平台的应用程序,从而显著降低了开发成本和时间投入。 丰富的类库和工具:CQt提供了广泛的类库和工具&…...

基于长短期神经网络LSTM的位移监测,基于长短期神经网络的位移预测,LSTM的详细原理
目录 背影 摘要 LSTM的基本定义 LSTM实现的步骤 基于长短期神经网络LSTM的位移监测 完整代码: https://download.csdn.net/download/abc991835105/88098131 效果图 结果分析 展望 参考论文 背影 路径追踪预测,对实现自动飞行驾驶拥有重要意义,长短期神经网络是一种改进党的…...
)
ChatGPT漫谈(二)
ChatGPT“脱胎”于OpenAI在2020年发布的GPT-3,任何外行都可以使用GPT-3,在几分钟内提供示例,并获得所需的文本输出。GPT-3被认为是当时最强大的语言模型,但现在,ChatGPT模型似乎更强大。ChatGPT能进行天马行空的长对话,可以回答问题,它具备了类人的逻辑、思考与沟通的能…...

【LangChain】检索器之MultiQueryRetriever
MultiQueryRetriever 概要内容总结 概要 基于距离的向量数据库检索在高维空间中嵌入查询,并根据“距离”查找相似的嵌入文档。 但是,如果查询措辞发生细微变化,或者嵌入不能很好地捕获数据的语义,检索可能会产生不同的结果。有时…...

教师ChatGPT的23种用法
火爆全网的ChatGPT,作为教师应该如何正确使用?本文梳理了教师ChatGPT的23种用法,一起来看看吧! 1、回答问题 ChatGPT可用于实时回答问题,使其成为需要快速获取信息的学生的有用工具。 从这个意义上说,Cha…...

【libevent】http客户端1:转存http下载的数据
read_http_input // // HTTP endpoint: GET /rpc/1 (list methods) or POST /rpc/1 (execute RPC) // // JSON-RPC API endpoint. Handles all JSON-RPC method calls. // static void rpc_jsonrpc(evhttp_request *req, void *opaque) {RpcApiInfo *ap =...
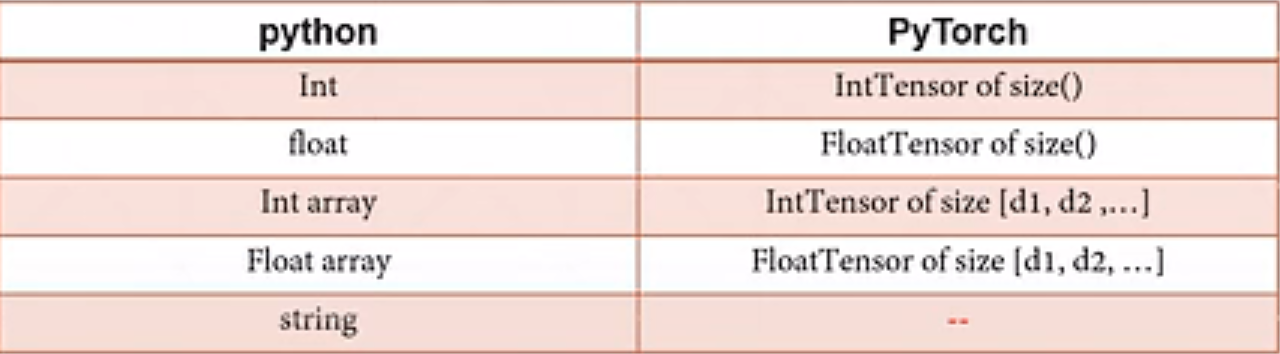
Pytorch学习笔记 | 数据类型 | mnist数据集
数据类型 python中数据类型和pytorch中的对应关系 注意:pytorch是没有没有string类型的 例1:创建一个3行4列的随机数数组,符合均值为0,方差为1的正态分布 import torch a=torch.Tensor(3,4) a Out[17]: tensor([[0....
Linux虚拟机(lvm)报Unmount and run xfs_repair
问题 linux系统没有正常关机,今天启动虚拟机无法进入系统,提示metadata corruption deleted at xxxx; Unmount and run xfs_repair 分析 主机异常掉电后里面的虚拟机无法启动,主要是损坏的分区 解决 看出来应该是dm-0分区损坏…...
【ESP32】Espressif-IDE及ESP-IDF安装
一、下载Espressif-IDE 2.10.0 with ESP-IDF v5.0.2 1.打开ESP-IDF 编程指南 2.点击快速入门–>安装–>手动安装–>Windows Installer–>Windows Installer Download 3.点击下载Espressif-IDE 2.10.0 with ESP-IDF v5.0.2 二、安装Espressif-IDE 2.10.0 wit…...

基于vue3实现画布操作的撤销与重做
基于vue3实现画布操作的撤销与重做 前言 vue3项目中实现在canvas画布上实现画节点和连线功能,要求可以撤销重做 思路 canvasBox 画板数据是存放在对象里面; snapshots存放操作记录; curIndex表示当前操作索引的下标; maxLimit表…...

php 抽象工厂模式
1,抽象工厂(Abstract Factory)模式,是创建设计模式的一种,它创建一系列相关的对象,而不必指定具体的类。该模式为一个产品族提供了统一的创建接口。当需要这个产品族的某一系列的时候,可以为此系…...

WPF实战学习笔记13-创建注册登录接口
创建注册登录接口 添加文件 创建文件 MyToDo.Api ./Controllers/LoginController.cs ./Service/ILoginService.cs ./Service/LoginService.cs MyToDo.Share ./Dtos/UserDto.cs LoginController.cs using Microsoft.AspNetCore.Mvc; using MyToDo.Api.Context;…...

银行API安全解决方案
数字经济背景下,外部市场环境的快速变化给商业银行带来很多不确定性,随着银行行业数字化转型进入深水区,银行经营面临新的机遇和挑战。 数字经济是传统银行向开放银行转型发展的重要支撑,开放银行旨在运用数字技术通过开放数据和…...

3d软件动物生活习性仿真互动教学有哪些优势
软体动物是一类广泛存在于海洋和淡水环境中的生物,其独特的形态和生活习性给学生带来了新奇和有趣的学习主题,为了方便相关专业学科日常授课教学,web3d开发公司深圳华锐视点基于真实的软体动物,制作软体动物3D虚拟展示系统&#x…...

<C语言> 字符串内存函数
C语言中对字符和字符串的处理很是频繁,但是C语言本身是没有字符串类型的,字符串通常放在常量字符串或者字符数组中。 字符串常量 适用于那些对它不做修改的字符串函数. 注意:字符串函数都需要包含头文件<string.h> 1.长度不受限制的…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
