OpenCV 对轮廓进行多边形逼近(Polygon Approximation)
在 OpenCV 中,cv::approxPolyDP 是一个函数,用于对轮廓进行多边形逼近(Polygon Approximation)。它可以将复杂的轮廓逼近为简化的多边形,从而减少轮廓的数据点,使轮廓更加紧凑。
函数原型如下:
cv::approxPolyDP(InputArray curve, OutputArray approxCurve, double epsilon, bool closed);
参数说明:
curve: 输入的轮廓点,可以是一个std::vector<cv::Point>或cv::Mat类型的数据。approxCurve: 输出的多边形逼近点,返回一个std::vector<cv::Point>或cv::Mat类型的数据,代表多边形逼近的点。epsilon: 控制逼近精度的参数。较小的值会产生更精细的逼近,较大的值会产生更简化的逼近。closed: 一个布尔值,用于指定多边形是否闭合。如果设置为true,则多边形是闭合的,如果设置为false,则多边形是非闭合的。
以下是一个简单的示例代码,演示如何使用 cv::approxPolyDP 对轮廓进行多边形逼近:
#include <opencv2/opencv.hpp>int main() {// 读取图像并转换为灰度图像cv::Mat image = cv::imread("path/to/your/image.jpg", cv::IMREAD_GRAYSCALE);// 二值化处理,将图像转换为黑白图像,以便寻找轮廓cv::Mat binary;cv::threshold(image, binary, 128, 255, cv::THRESH_BINARY);// 寻找轮廓std::vector<std::vector<cv::Point>> contours;cv::findContours(binary, contours, cv::RETR_EXTERNAL, cv::CHAIN_APPROX_SIMPLE);// 多边形逼近std::vector<std::vector<cv::Point>> approxContours(contours.size());for (size_t i = 0; i < contours.size(); ++i) {cv::approxPolyDP(contours[i], approxContours[i], 5, true); // 使用 epsilon = 5 进行多边形逼近}// 绘制轮廓和多边形逼近cv::Mat result;cv::cvtColor(binary, result, cv::COLOR_GRAY2BGR);cv::drawContours(result, contours, -1, cv::Scalar(0, 0, 255), 2); // 绘制原始轮廓(红色)cv::drawContours(result, approxContours, -1, cv::Scalar(0, 255, 0), 2); // 绘制多边形逼近(绿色)// 显示结果cv::imshow("Original and Approximated Contours", result);cv::waitKey(0);return 0;
}
在上述示例中,我们首先读取图像并转换为灰度图像,然后进行二值化处理,找到图像中的轮廓。接着,使用 cv::approxPolyDP 对每个轮廓进行多边形逼近,并绘制原始轮廓(红色)和多边形逼近(绿色)的结果。
使用 Python 和 OpenCV 实现多边形逼近的示例代码:
import cv2
import numpy as np# 读取图像并转换为灰度图像
image = cv2.imread("path/to/your/image.jpg", cv2.IMREAD_GRAYSCALE)# 二值化处理,将图像转换为黑白图像,以便寻找轮廓
_, binary = cv2.threshold(image, 128, 255, cv2.THRESH_BINARY)# 寻找轮廓
contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)# 多边形逼近
approxContours = []
for contour in contours:epsilon = 0.01 * cv2.arcLength(contour, True) # epsilon 控制逼近精度的参数approx = cv2.approxPolyDP(contour, epsilon, True)approxContours.append(approx)# 绘制轮廓和多边形逼近
result = cv2.cvtColor(binary, cv2.COLOR_GRAY2BGR)
cv2.drawContours(result, contours, -1, (0, 0, 255), 2) # 绘制原始轮廓(红色)
cv2.drawContours(result, approxContours, -1, (0, 255, 0), 2) # 绘制多边形逼近(绿色)# 显示结果
cv2.imshow("Original and Approximated Contours", result)
cv2.waitKey(0)
cv2.destroyAllWindows()
在 Python 版本的代码中,我们使用了 cv2.threshold 函数进行二值化处理,使用 cv2.findContours 函数找到图像中的轮廓,然后通过 cv2.approxPolyDP 函数对每个轮廓进行多边形逼近。最后,使用 cv2.drawContours 函数将原始轮廓和多边形逼近结果绘制在图像上,并显示结果。
Python 版本的代码与 C++ 版本的代码相比,在函数调用时稍有不同,但整体逻辑是相同的。
相关文章:
)
OpenCV 对轮廓进行多边形逼近(Polygon Approximation)
在 OpenCV 中,cv::approxPolyDP 是一个函数,用于对轮廓进行多边形逼近(Polygon Approximation)。它可以将复杂的轮廓逼近为简化的多边形,从而减少轮廓的数据点,使轮廓更加紧凑。 函数原型如下:…...
Docker的数据管理和Dockerfile的指令
Docker的数据管理 一、Docker数据的概念1、数据卷2、数据卷容器 二、端口映射三、容器互联(使用centos镜像)四、Docker 镜像的创建1、基于现有镜像创建(1)首先启动一个镜像,在容器里做修改(2)然…...

[SQL挖掘机] - 交叉连接: cross join
介绍: 交叉连接是一种多表连接方式,它返回两个表的笛卡尔积,即将一个表的每一行与另一个表的每一行进行组合。换句话说,交叉连接会生成一个包含所有可能组合的结果集。 交叉连接的工作原理如下:它会将左表的每一行与右表的每一行…...
Python web实战 | 使用 Django 搭建 Web 应用程序 【干货】
概要 从社交媒体到在线购物,从在线银行到在线医疗,Web 应用程序为人们提供了方便快捷的服务。Web 应用程序已经成为了人们日常生活中不可或缺的一部分。搭建一个高效、稳定、易用的 Web 应用程序并不是一件容易的事情。本文将介绍如何使用 Django 快速搭…...
)
UE5自定义蓝图节点(二)
继承于UBlueprintAsyncActionBase的类,异步输出节点的实现方法,代码测试正常 .h // Fill out your copyright notice in the Description page of Project Settings.#pragma once#include "CoreMinimal.h" #include "Kismet/BlueprintA…...

Bean容器中的ThreadPoolTaskExecutor需要手动关闭吗
ThreadPoolTaskExecutor 是 Spring 提供的一个方便的线程池实现,用于异步执行任务或处理并发请求。 在使用 ThreadPoolTaskExecutor 作为 Spring Bean 注册到容器中后,Spring 会负责在应用程序关闭时自动关闭所有注册的线程池,所以不需要手动…...
——Redis的Java客户端)
Redis学习路线(3)——Redis的Java客户端
一、如何使用Redis的Java客户端 官方文档: https://redis.io/docs/clients/java/ Java-Redis客户端使用场景Jeids 以Redis命令作为方法名称,学习成本低,简单实现,但是Jedis实例是线程不安全的,多线程环境下需要基于连…...
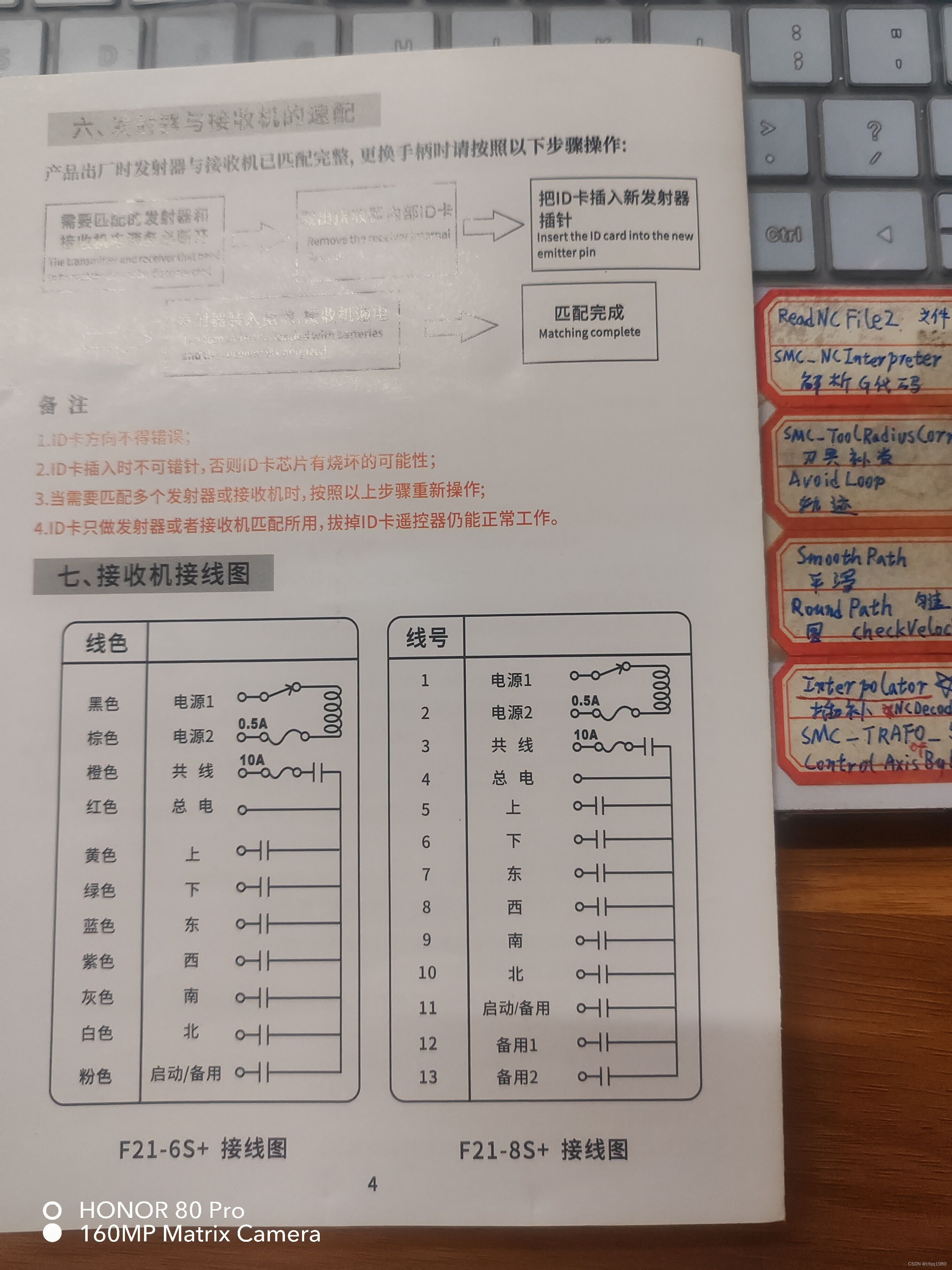
行车遥控接线图
这个一般只有电工才会用。 主要是 【共线和总电】让人疑惑。 这图实际就是PLC的梯形图。 共电:接主电源。【它串联10A保险丝,再到继电器】 总电:它是所有继电器的公共端。【共电的继电器吸合,共电和总电就直通了。】共电的继电器…...

区块链实验室(11) - PBFT耗时与流量特征
以前面仿真程序为例,分析PBFT的耗时与流量特征。实验如下,100个节点构成1个无标度网络,节点最小度为5,最大度为38. 从每个节点发起1次交易共识。统计每次交易的耗时以及流量。本文所述的流量见前述仿真程序的说明:区块链实验室(3)…...
环境变量 位置变量 系统内置变量)
Shell编程基础(三)环境变量 位置变量 系统内置变量
环境变量 & 环境变量环境变量范围父子进程之间有效指定用户有效所有用户有效 位置变量系统内置变量 环境变量 在脚本种直接定义的变量,只能在当前shell进程中使用 若想要在其他shell进程中使用,可以将变量声明为 环境变量 export 变量名 ÿ…...

P5718 【深基4.例2】找最小值
题目描述 给出 n n n 和 n n n 个整数 a i a_i ai,求这 n n n 个整数中最小值是什么。 输入格式 第一行输入一个正整数 n n n,表示数字个数。 第二行输入 n n n 个非负整数,表示 a 1 , a 2 … a n a_1,a_2 \dots a_n a1,a2……...
C++——STL容器之list链表的讲解
目录 一.list的介绍 二.list类成员函数的讲解 2.2迭代器 三.添加删除数据: 3.1添加: 3.2删除数据 四.排序及去重函数: 错误案例如下: 方法如下: 一.list的介绍 list列表是序列容器,允许在序列内的任何…...

使用for循环输出左上三角、右上三角、左下三角、右下三角、上下三角
1、输出如下图形: #include<stdio.h> int main() {/*输出图形 666666666666666*/for(int i1;i<5;i){for(int j1;j<i;j){putchar(6);}printf("\n"); } return 0; } 2、输出如下图形: #include<stdio.h> int main() {/*输出图…...
CAXA中.exb或者.dwg文件保存为PDF
通常CAXAZ中的文件为.exb或者.dwg格式,我们想打印或者保存为PDF文件格式,那么就用一下的方法: CAXA文件如图所示: 框选出你要打印的图纸!!!! 我们选择"菜单"->"…...

华为刷题:HJ3明明随机数
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main {public static void main(String[] args) {Scanner scan new Scanner(System.in);int N scan.nextInt();int[] arr new int[N];for (int i 0; i < N; i) {int n sca…...
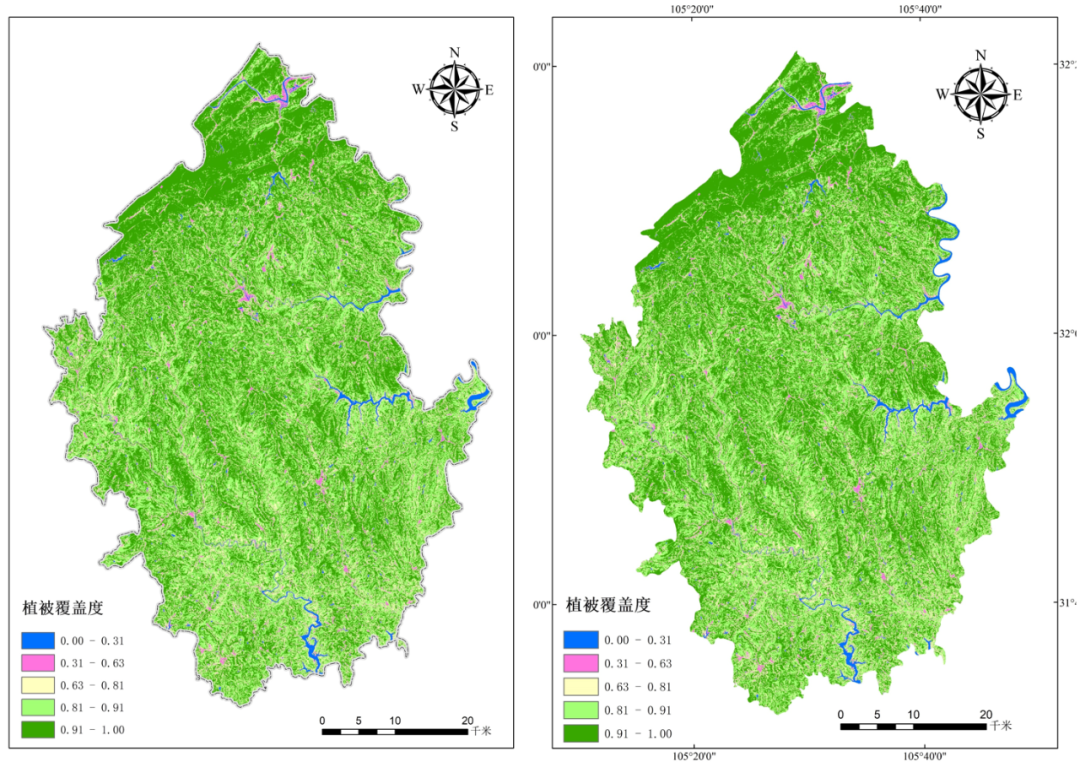
ENVI提取NDVI与植被覆盖度估算
目标是通过ENVI计算植被覆盖度结合ArcGIS出图得到植被覆盖图。 一、植被覆盖度的定义: 植被覆盖度( FractionalVegetation Cover,FVC) 通常定义为植被( 包括叶、茎、枝) 在地面的垂直投影面积占统计区总面积的百分比,它量化了植被的茂密程度,反应了植被的生长态势,是刻画…...

Arm 扩大开源合作伙伴关系,加强投入开放协作
作者:Arm 开源软件副总裁 Mark Hambleton Arm 和我们的生态系统的关键信念之一是与开源社区合作,共创一个高度发达的 Arm 架构,使软件的落地更加稳定,从而让全球数百万开发者能够测试并创建自己的应用。 为此,Arm 支…...

Kubernetes 的核心概念:Pod、Service 和 Namespace 解析
🌷🍁 博主 libin9iOak带您 Go to New World.✨🍁 🦄 个人主页——libin9iOak的博客🎐 🐳 《面试题大全》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~ἳ…...
互联网搜索的学习笔记
1. 参考资料 《Internet Search Tips》《Google Search Operators: The Complete List (42 Advanced Operators)》 2. 预备知识 2.1 查询语法 2.1.1 -:排除符 用于排除指定关键字。例如,如果想搜索“苹果”但不想看到“苹果手机”的结果,…...

vue事件修饰符
vue事件修饰符 1、目标2、语法 1、目标 在事件后面.修饰符名-给事件带来强大功能 2、语法 事件名.修饰符“methods里的函数” 修饰符列表 .stop - 阻止事件冒泡 示例: <template><div id"app"><div click"fatherFn"><…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
