前端CryptoJS-AES加解密 对应php的AES-128-CBC加解密踩坑(java也相同加解密)
前端部分注意看填充是pkcs7
有个前提,要看前端有没有转成hex格式,如果没转,php那边就不需要调用特定函数转hex格式的
const keyStr = '5hOwdHxpW0GOciqZ';const iv = '0102030405060708';//加密function Encrypt(word) {let key = CryptoJS.enc.Utf8.parse(keyStr);let srcs = CryptoJS.enc.Utf8.parse(word);let encrypted = CryptoJS.AES.encrypt(srcs, key, {iv: CryptoJS.enc.Utf8.parse(iv),mode: CryptoJS.mode.CBC,padding: CryptoJS.pad.Pkcs7});let hexStr = encrypted.ciphertext.toString().toUpperCase();return hexStr.toString();// encrypted.ciphertext.toString(); // 返回hex格式的密文//encrypted.toString(); //此方式返回base64格式密文}//解密function Decrypt(word) {let key = CryptoJS.enc.Utf8.parse(keyStr);let encryptedHexStr = CryptoJS.enc.Hex.parse(word);var srcs = CryptoJS.enc.Base64.stringify(encryptedHexStr);let decrypt = CryptoJS.AES.decrypt(srcs, key, {iv: CryptoJS.enc.Utf8.parse(iv),mode: CryptoJS.mode.CBC,padding: CryptoJS.pad.Pkcs7});return CryptoJS.enc.Utf8.stringify(decrypt).toString();}后端php代码
if (!function_exists('encrypt')) {//加密function encrypt($data, $method = 'AES-128-CBC', $typeNum = 1){$key = '5hOwdHxpW0GOciqZ';$iv = '0102030405060708';$a = openssl_encrypt($data, $method, $key, $typeNum, $iv);// $base64 = base64_encode(openssl_encrypt($data, $method, $key, $typeNum, $iv));//先转hex格式 再转大写模式return strtoupper(bin2hex($a)); }
}if (!function_exists('decrypt')) {//解密 这里 $typeNum必须为0function decrypt($data, $method = "AES-128-CBC", $typeNum = 0){$key = '5hOwdHxpW0GOciqZ';$iv = '0102030405060708';$data = base64_encode(hex2bin($data));$a = openssl_decrypt($data, $method, $key, $typeNum, $iv);return $a;}
}相关文章:
)
前端CryptoJS-AES加解密 对应php的AES-128-CBC加解密踩坑(java也相同加解密)
前端部分注意看填充是pkcs7 有个前提,要看前端有没有转成hex格式,如果没转,php那边就不需要调用特定函数转hex格式的 const keyStr 5hOwdHxpW0GOciqZ;const iv 0102030405060708;//加密function Encrypt(word) {let key CryptoJS.enc.Ut…...

Python解码张三的法外狂徒之旅,揭秘视频背后的真相!【含jS逆向解密】
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 传说中,有人因为只是远远的看了一眼法外狂徒张三就进去了😂 我现在是获取他视频,岂不是直接终生了🤩 网友:赶紧跑路吧 😏 好了话不多说ÿ…...

【解析】对比学习和孪生网络的关系
文章目录 区别联系具体概念孪生网络(Siamese Networks)对比学习(Contrastive Learning) 区别 孪生网络是一种特定的神经网络结构;对比学习是一种学习策略,它试图让模型学习如何区分正样本对(相…...

Java版本企业工程项目管理系统平台源码(三控:进度组织、质量安全、预算资金成本、二平台:招采、设计管理)
工程项目管理软件(工程项目管理系统)对建设工程项目管理组织建设、项目策划决策、规划设计、施工建设到竣工交付、总结评估、运维运营,全过程、全方位的对项目进行综合管理 工程项目各模块及其功能点清单 一、系统管理 1、数据字典&#…...

智能井盖:科技赋能城市脚下安全
在智能化飞速发展的今天,智能井盖作为城市基础设施的一部分,正逐渐走进人们的视野。它利用现代科技手段,实现了对城市井盖的实时监控、及时响应和高效管理,为城市管理、市民出行等方面带来了诸多便利。 城市中井盖数量庞大&#x…...

wangeditor编辑器配置
vue项目中使用编辑器,轻量,操作栏选取自己需要的 官网地址:用于 Vue React | wangEditor 使用在vue项目中引入 npm install wangeditor/editor --savenpm install wangeditor/editor-for-vue --save 封装成组件使用 <template>&…...

Sqlite使用WAL模式指南
本文地址:http://t.csdn.cn/kE8ND 文章目录 一、WAL模式的原理二、开启WAL后必须要设置的参数1.PRAGMA SYNCHRONOUS(1)SYNCHRONOUS的类型(2)WAL下如何选择SYNCHRONOUS类型 2.PRAGMA wal_autocheckpoint3.sqlite3_busy…...

一套高质量可靠的 React Hooks 库
个人使用,感受,挺好用 https://ahooks.js.org/zh-CN 我主要用了这个 useCountDown 倒计时,再也不用费心费力去写一个倒计时方法了,而且直接提供end之后要做什么。...
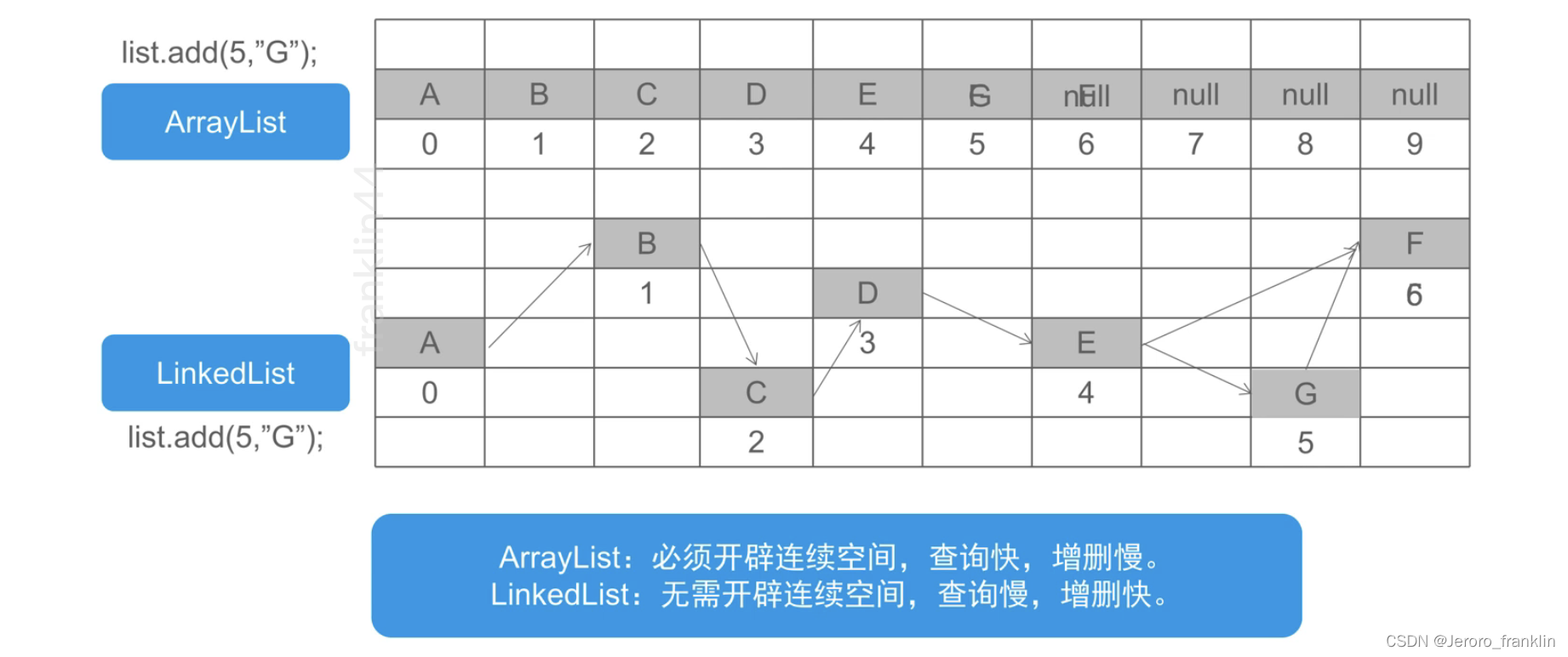
集合---list接口及实现类
一、list概述 1、list接口概述 List接口继承自Collection接口,是单列集合的一一个重要分支,我们习惯性地会将实现了 List接口的对象称为List集合。在List集合中允许出现重复的元素,所有的元素是以一种线性方 式进行有序存储的,在…...
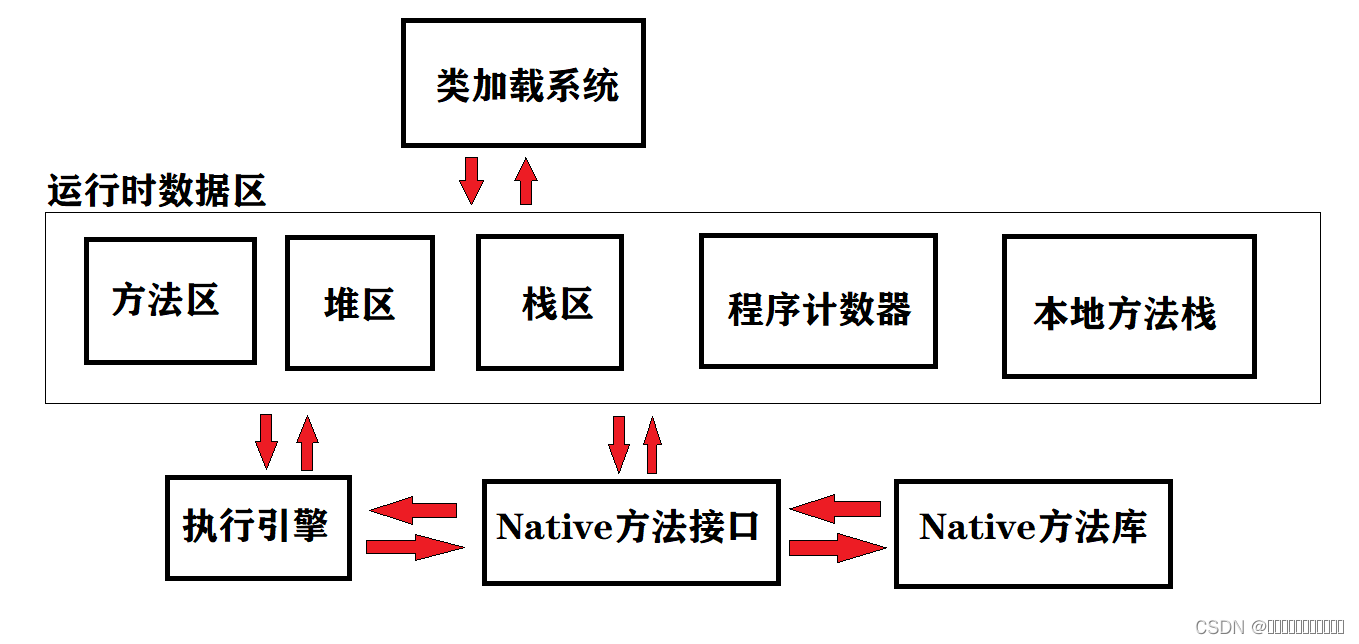
JVM简述
JDK&JRE&JVMJVM运行时内存结构图方法区堆区栈区程序计数器本地方法栈 JVM 的主要组成部分及其作用 JDK&JRE&JVM JVM就是java虚拟机,一台虚拟的机器,用来运行java代码 但并不是只有这台机器就可以的,java程序在运行时需要依赖…...

7.25训练总结
考场错误: A题其实并不简单,但是先想了一个方法后,就交了,wa了后一直卡住,策略不当,到最后后期写C的时候也犯了一些低级的错误,这点需要注意。 之后顺利的把BCDHI写完后,又完成了A的…...
java注解@FeignClient修饰的类路径不在spring boot入口类所在的包下,有哪几种处理方式?
一、注解EnableFeignClients 修饰在spring boot入口类,使得openfeign的FeignClient注解生效。 我们进一步看看注解EnableFeignClients的使用方式。 String[] basePackages() default {};Class<?>[] basePackageClasses() default {};Class<?>[] clie…...

神经网络随记-参数矩阵、剪枝、模型压缩、大小匹配、、
神经网络的参数矩阵 在神经网络中,参数矩阵是模型学习的关键部分,它包含了神经网络的权重和偏置项。下面是神经网络中常见的参数矩阵: 权重矩阵(Weight Matrix):权重矩阵用于线性变换操作,将输…...

4、Kubernetes 集群 YAML 文件详解
目录 一、YAML 概述 二、YAML 基本语法 三、YAML 数据结构 四、k8s资源清单描述方法 五、YAML 快速编写 1、使用 kubectl create 命令 2、使用 kubectl get 命令导出 yaml 文件 一、YAML 概述 k8s 集群中对资源管理和资源对象编排部署都可以通过声明YAML文件来解决&…...
)
leetcode93. 复原 IP 地址(java)
复原 IP 地址 leetcode93. 复原 IP 地址回溯算法代码演示 回溯算法 leetcode93. 复原 IP 地址 有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 ‘.’ 分隔。 例如:“0.1.2…...

极光Java 版本服务器端实现别名消息推送
文章目录 引言I 概述1.1 依赖包1.2 极光证书环境参数1.3 构建推送对象II 推送内容2.1 配置推送内容2.2 获取通知消息内容2.3 配置IOS通知内容2.4 配置Android通知内容2.5 发起推送2.6 分批推送2.7 初始化密钥2.8 配置密钥引言 REST API 文档:https://docs.jiguang.cn/jpush/se…...

【Lua学习笔记】Lua进阶——Table(4)继承,封装,多态
文章目录 封装继承多态 封装 // 定义基类 Object {}//由于表的特性,该句就相当于定义基类变量 Object.id 1//该句相当于定义方法,Object可以视为定义的对象,Test可以视为方法名 //我们知道Object是一个表,但是抽象地看ÿ…...
Linux中常用的指令
ls ls [选项] [目录或文件] 功能:对于目录,列出该目录下所有的子目录和文件;对于文件,列出该文件的文件名和其他属性 常用选项: -a:列出目录下的所有文件,包括以.开头的隐藏文件 -l:列出文件的详细信息。…...
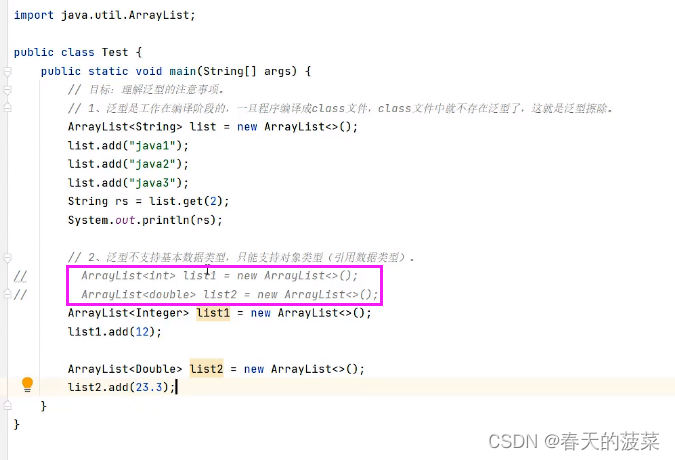
【java】【面对对象高级4】内部类、枚举、泛型
目录 1、内部类 1.1 成员内部类【了解】 1.1.1 定义 1.1.2 扩展变量 1.2 静态内部类【了解】 1.2.1 定义 1.2.2 扩展变量 1.3 局部内部类【了解】 1.4 匿名内部类【重点】 1.4.1 定义 1.4.1.1 常规写法 1.4.1.2 匿名内部类改造 1.4.2 匿名内部类的常见使用场景 1.4.2…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...

