【数据结构与算法】数组2:双指针法 二分法(螺旋矩阵)
文章目录
- 今日任务
- 1.Leetcode977:有序数列的平方
- (1)题目
- (2)思路
- (3)暴力排序
- (4)双指针法
- 2.Leetcode209:长度最小的子数组
- (1)题目
- (2)思路
- (3)暴力排序
- (4)滑动窗口
- 3.Leetcode59:螺旋矩阵II
- (1)题目
- (2)思路
- (3)二分法求解
今日任务
-
977.有序数列的平方
-
209.长度最小的子数组
-
59.螺旋矩阵II
1.Leetcode977:有序数列的平方
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/squares-of-a-sorted-array
(1)题目
**给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 **
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
提示:
- 1 <= nums.length <= 104
- -104 <= nums[i] <= 104
- nums 已按 非递减顺序 排序
进阶:
请你设计时间复杂度为 O(n) 的算法解决本问题
(2)思路
最开始的一个想法,就是首先对每个数进行平方,然后再对新数组进行排序。
(3)暴力排序
有了昨天的经验,我们可以直接使用暴力排序的方式进行编程:
class Solution {
public:vector<int> sortedSquares(vector<int>& nums) {for(int i = 0; i < nums.size(); i++){// nums[i] = pow(abs(nums[i]),2);nums[i] *= nums[i];}sort(nums.begin(),nums.end());return nums;}
};
说明:
- pow(a,b):a作为目标值,b作为指数,是用作指数运算,例如pow(2,2)—>2^2=4;
- abs(n):对n求绝对值
解答:上面的求平方数我用了两种方式求解,但是很明显可以看出注释的那一段代码明显执行的时间复杂度更高,也就是O(nlogn+1+nlog2n),而另外的一种方式的时间复杂度则是O(n+nlogn)
**在这里也有大佬提出:二分法的log2就直接logn就可以,平衡二叉树 排序都直接nlogn就行 **
(4)双指针法
根据数组最大值通过平方之后,不是最大值就是最小值,我们可以考虑使用双指针法,i指向起始位置,j指向终止位置。
- 定义一个新数组result,和数组A一样的大小,让
K指向result数组终止位置 - 如果A[i] *A[i] < A[j] * A[j],那么result[k–] = A[j] * A[j];
- 如果A[i] *A[i] > A[j] * A[j],那么result[k–] = A[i] * A[i];
class Solution {
public:vector<int> sortedSquares(vector<int>& nums) {vector<int> result(nums.size(),0);int k = nums.size() - 1;for(int i = 0,j = nums.size() - 1; i <= j; ){if(nums[i] * nums[i] < nums[j] * nums[j]){result[k--] = nums[j] * nums[j];j--;}else{result[k--] = nums[i] * nums[i];i++;}}return result;}
};
通过双指针法求解有序数列的平方,此时的时间复杂度为O(n),相比较暴力排序这个还是更加推荐!
2.Leetcode209:长度最小的子数组
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/minimum-size-subarray-sum
(1)题目
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
- 1 <= target <= 109
- 1 <= nums.length <= 105
- 1 <= nums[i] <= 105
进阶:
如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。
(2)思路
首先分析题意,最明显的就是要求是连续子数组,然后就是要求这个子数组长度最小,遇到这个问题,我们想到的就是首先分出若干个有效子数组(要求是连续的),然后对这些子数组的长度进行筛选,留下长度最小的返回该数组长度。
(3)暴力排序
对这道题暴力排序的解法是通过使用两个for循环,然后不断寻找符合条件的子序列,具体判断时间复杂度是O(n^2)。
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int result = INT32_MAX; // 最终的结果int sum = 0; // 子序列的数值之和int subLength = 0; // 子序列的长度for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为isum = 0;for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为jsum += nums[j];if (sum >= target) { // 一旦发现子序列和超过了s,更新resultsubLength = j - i + 1; // 取子序列的长度result = result < subLength ? result : subLength;break; // 因为我们是找符合条件最短的子序列,所以一旦符合条件就break}}}// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列return result == INT32_MAX ? 0 : result;}
};
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
对于这部分的暴力排序其实有些还没看懂,先在这插个眼,并且根据力扣的测试,该方法已经超时,应该是不建议使用。
(4)滑动窗口
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们想要的结果。
那怎么理解滑动窗口呢,其实滑动窗口的做法也可以作为双指针法的一种,通过动态变换滑动窗口的起始和终止位置构成的滑动区域,依次遍历可能出现的子数组。
那么最重要的两点来了:
- 如何确定移动窗口的起始位置
- 如何确定移动窗口的结束位置
解答如下:
- 窗口的起始位置如何移动:如果当前窗口的值大于target,说明已经找到一种满足情况的子数组了,那么此时应该将窗口向前移动
- 窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,也就是给定数组下标的最大值
class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int result = INT32_MAX;int sum = 0; // 滑动窗口数值之和int i = 0; // 滑动窗口起始位置int subLength = 0; // 滑动窗口的长度for (int j = 0; j < nums.size(); j++) {sum += nums[j];// 注意这里使用while,每次更新 i(起始位置),并不断比较子序列是否符合条件while (sum >= target) {subLength = (j - i + 1); // 取子序列的长度result = result < subLength ? result : subLength;sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处,不断变更i(子序列的起始位置)}}// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列return result == INT32_MAX ? 0 : result;}
};
在这里的话也才发现滑动窗口这个算法精妙所在,通过不断变更一个窗口的位置,将算法的复杂度明显优化,而且相比较暴力排序,滑动窗口也只用了一个for循环和一个while循环,从而将算法复杂度降为O(n)
3.Leetcode59:螺旋矩阵II
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/spiral-matrix-ii
(1)题目
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
提示:
- 1 <= n <= 20
(2)思路
在这里悉心听取Carl大神的教诲,每次遇到二分法一定要坚持循环不变量原则。
那么我们在模拟顺时针画矩阵时,遵循以下规则:
- 填充上行从左往右
- 填充右列从上往下
- 填充下行从右往左
- 填充左列从下往上
也就是如下图所示,好好理解一下!

回到题目,对于这种螺旋矩阵,我们首先要明确的坚持循环不变量原则,要么选择左闭右闭,要么选择左闭右开,选择好一种处理方式就贯彻到底,不要再做改变了。
这里我们选择左闭右开,首先还是看到上面的螺旋矩阵图,我们分别将3X3矩阵内的所有元素切割为9个部分,解决螺旋矩阵问题,最重要就是确定外围的四个点,即图中的1、3、5、7,前面我们说我们遵循左闭右开规则,其实意思就是对左节点进行处理,而右节点暂不处理,而等待下一次处理时将第一次的右节点作为第二次的左节点,这样就是我们所说的左闭右开原则。
(3)二分法求解
直接看代码部分:
class Solution {
public:vector<vector<int>> generateMatrix(int n) {vector<vector<int>> res(n, vector<int>(n, 0)); // 使用vector定义一个二维数组int startx = 0, starty = 0; // 定义每循环一个圈的起始位置int loop = n / 2; // 每个圈循环几次,例如n为奇数3,那么loop = 1 只是循环一圈,矩阵中间的值需要单独处理int mid = n / 2; // 矩阵中间的位置,例如:n为3, 中间的位置就是(1,1),n为5,中间位置为(2, 2)int count = 1; // 用来给矩阵中每一个空格赋值int offset = 1; // 需要控制每一条边遍历的长度,每次循环右边界收缩一位int i,j;while (loop --) {i = startx;j = starty;// 下面开始的四个for就是模拟转了一圈// 模拟填充上行从左到右(左闭右开)for (j = starty; j < n - offset; j++) {res[startx][j] = count++;}// 模拟填充右列从上到下(左闭右开)for (i = startx; i < n - offset; i++) {res[i][j] = count++;}// 模拟填充下行从右到左(左闭右开)for (; j > starty; j--) {res[i][j] = count++;}// 模拟填充左列从下到上(左闭右开)for (; i > startx; i--) {res[i][j] = count++;}// 第二圈开始的时候,起始位置要各自加1, 例如:第一圈起始位置是(0, 0),第二圈起始位置是(1, 1)startx++;starty++;// offset 控制每一圈里每一条边遍历的长度offset += 1;}// 如果n为奇数的话,需要单独给矩阵最中间的位置赋值if (n % 2) {res[mid][mid] = count;}return res;}
};
相关文章:

【数据结构与算法】数组2:双指针法 二分法(螺旋矩阵)
文章目录今日任务1.Leetcode977:有序数列的平方(1)题目(2)思路(3)暴力排序(4)双指针法2.Leetcode209:长度最小的子数组(1)题目&#x…...

librtmp优化
librtmp是一个RTMP的开源库,很多地方用它来做推流、拉流。它是RTMPDump开源软件里的一部分,librtmp的下载地址:RTMPDump,目前最新版是V2.3。本文重点介绍librtmp优化。 1、调整网络输出块大小。 RTMP_Connect0函数中LibRTMP是关…...

数据结构与算法(二):线性表
上一篇《数据结构与算法(一):概述》中介绍了数据结构的一些基本概念,并分别举例说明了算法的时间复杂度和空间复杂度的求解方法。这一篇主要介绍线性表。 一、基本概念 线性表是具有零个或多个数据元素的有限序列。线性表中数据…...
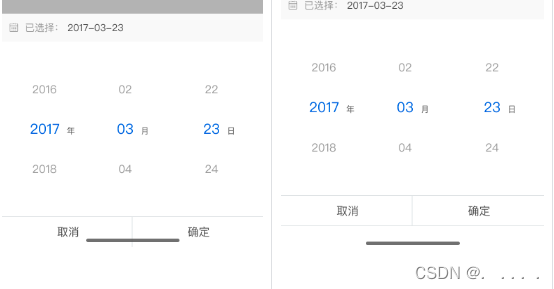
IOS安全区域适配
对于 iPhone 8 和以往的 iPhone,由于屏幕规规整整的矩形,安全区就是整块屏幕。但自从苹果手机 iphoneX 发布之后,前端人员在开发移动端Web页面时,得多注意一个对 IOS 所谓安全区域范围的适配。这其实说白了就是 iphoneX 之后的苹果…...
在Java 中 利用Milo通信库,实现OPCUA客户端,并生成证书
程序结构: 配置文件resources: opcua.properties 西门子PLC端口号为4840,kepserver为49320 #opcua服务端配置参数 #opcua.server.endpoint.urlopc.tcp://192.168.2.102:49320 opcua.server.endpoint.urlopc.tcp://192.168.2.11:4840 opcu…...

三分钟学会用Vim
Vim知识点 目录Vim知识点一:什么是vim二:vim常用的三种模式三:vim的基本操作一:什么是vim vim最小集 vim是一款多模式的编辑器—各种模式—每种模式的用法有差别—每种模式之间可以互相切换 但是我们最常用的就是3~5个模式 vi…...
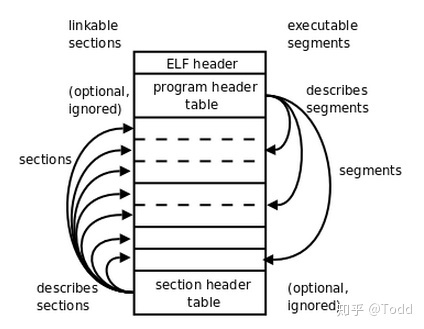
编译链接实战(8)认识elf文件格式
🎀 关于博主👇🏻👇🏻👇🏻 🥇 作者简介: 热衷于知识探索和分享的技术博主。 💂 csdn主页::【奇妙之二进制】 ✍️ 微信公众号:【Linux …...

新手小白如何入门黑客技术?
你是否对黑客技术感兴趣呢?感觉成为黑客是一件很酷的事。那么作为新手小白,我们该如何入门黑客技术,黑客技术又是学什么呢? 其实不管你想在哪个新的领域里有所收获,你需要考虑以下几个问题: 首先ÿ…...
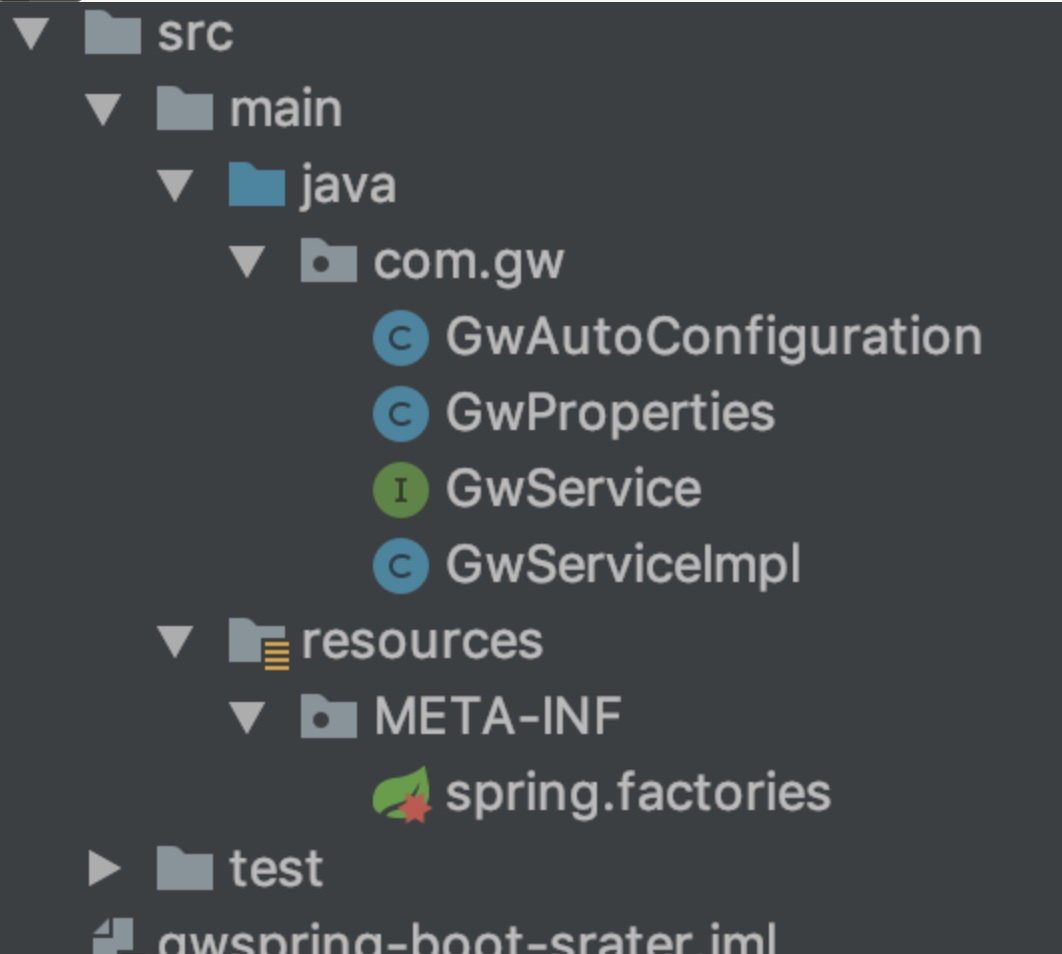
【java】Spring Boot --深入SpringBoot注解原理及使用
步骤一 首先,先看SpringBoot的主配置类: SpringBootApplication public class StartEurekaApplication {public static void main(String[] args){SpringApplication.run(StartEurekaApplication.class, args);} }步骤二 点进SpringBootApplication来…...
一文掌握如何对项目进行诊断?【步骤方法和工具】
作为项目经理和PMO,面对错综复杂的项目,需要对组织的项目运作情况进行精确的分析和诊断,找出组织项目管理中和项目运行中存在的问题和潜在隐患,分析其原因,预防风险,并且形成科学合理的决策建议和解决方案&…...

系统分析师真题2020试卷相关概念二
结构化设计相关内容: 结构化设计是一种面向数据流的系统设计方法,它以数据流图和数据字典等文档为基础。数据流图从数据传递和加工的角度,以图形化方式来表达系统的逻辑功能、数据在系统内部的逻辑流向和逻辑变换过程,是结构化系统分析方法的主要表达工具及用于表示软件模…...
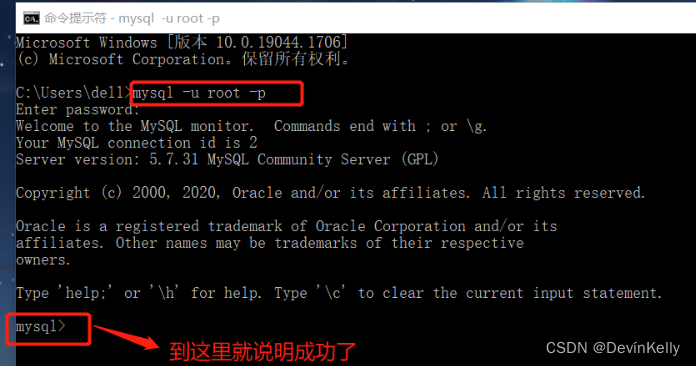
<<Java开发环境配置>>5-MySQL安装教程(绿色版)
一.MySQL绿色版安装: 1.直接解压下载的ZIP文件到对应的目录下(切记安装目录不要有中文); 如图:我的安装目录:D:Program Files 2.创建配置文件: 在MySQL安装目录下,创建一个my.ini配置文件,然后在里面添加以下内容(别忘了MySQL安装目录要改成…...

空间复杂度与时间复杂度
1、时间复杂度和空间复杂度 (1)时间复杂度、空间复杂度是什么? 算法效率分析分为两种:第一种是时间效率,第二种是空间效率。时间效率被称为时间复杂度,空间效率被称作空间复杂度时间复杂度主要衡量的是一…...

javaEE 初阶 — 延迟应答与捎带应答
文章目录1. 延迟应答2. 捎带应答TCP 工作机制:确认应答机制 超时重传机制 连接管理机制 滑动窗口 流量控制与拥塞控制 1. 延迟应答 延时应答 也是提升效率的机制,也是在滑动窗口基础上搞点事情。 滑动窗口的关键是让窗口大小大一点,传输…...

Twitter账号老被封?一文教会你怎么养号
昨天龙哥给大家科普完要怎么批量注册Twitter账号,立刻有朋友来私信龙哥说里面提到的这个养号和防关联具体是个怎么样的做法。由于Twitter检测机制还是比较敏感的,账号很容易被冻结,所以养号是非常重要的步骤。其实要养好Twitter账号其实并不难…...

当遇到国外客户的问题,你解决不了的时候怎么办
对我来说,今年的这个春节假期有点长,差不多休了一个月。复工之后,截止目前做到了60万RMB的业绩,但是相较于往年,整体状态还是差了些。往年的春节,我都是随时待命的状态,整个春节天天坐于电脑前&…...
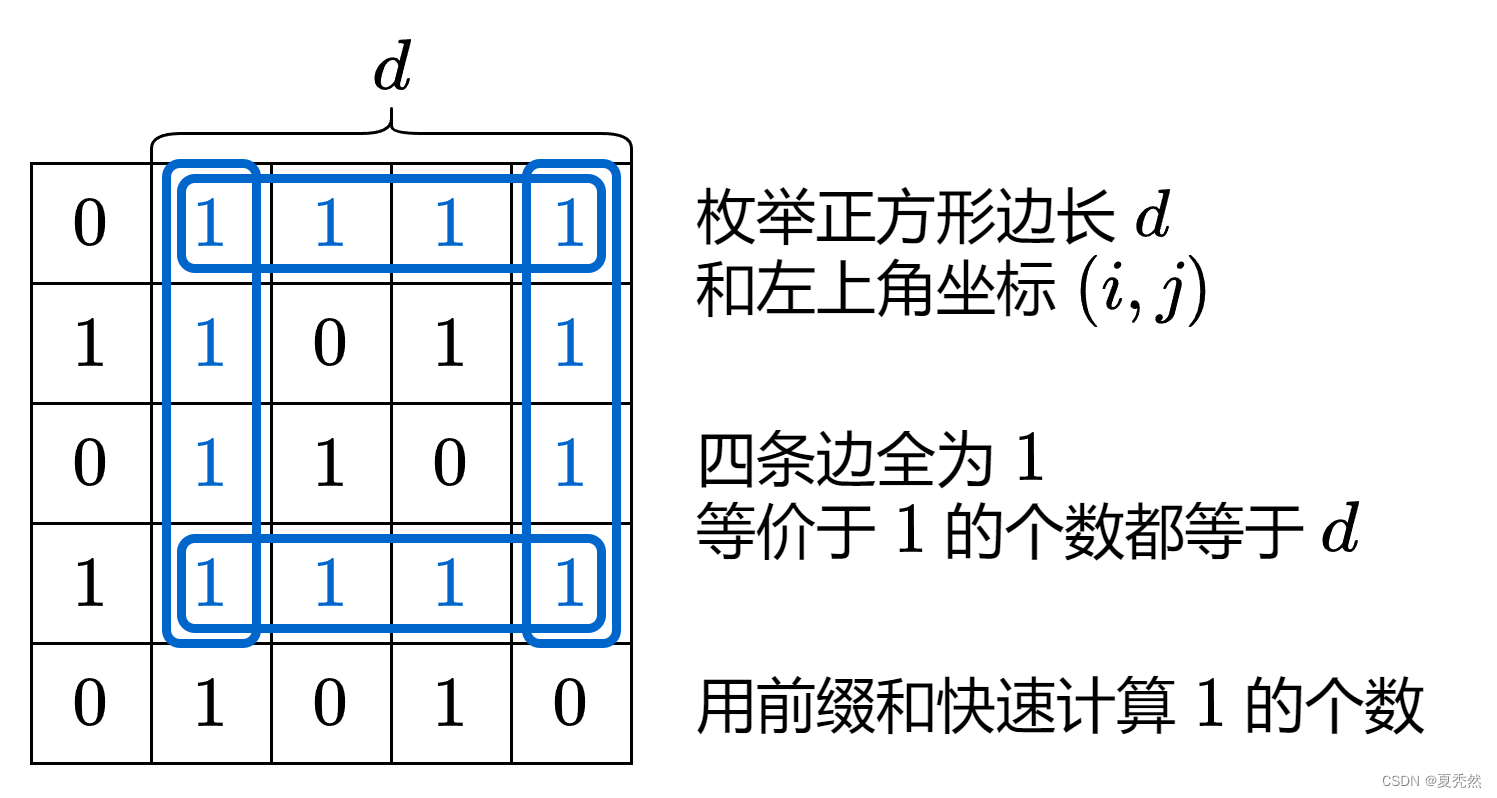
算法刷题打卡第93天: 最大的以 1 为边界的正方形
最大的以 1 为边界的正方形 难度:中等 给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。 示例 1: 输入:…...
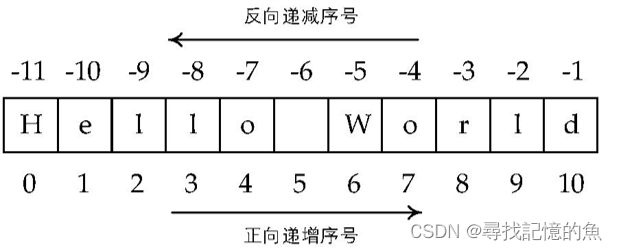
python语言基础(最详细版)
文章目录一、程序的格式框架缩进1、定义2、这里就简单的举几个例子注释二、语法元素的名称三、数据类型四、数值运算符五、关系运算六、逻辑运算七、运算符的结合性八、字符串一、程序的格式框架 缩进 1、定义 (1)python中通常用缩进来表示代码包含和…...

Java小技能:字符串
文章目录 引言I 预备知识1.1 Object类1.2 重写的规则1.3 hashCode方法II String2.1 String的特性2.2 字符串和正则2.3 StringBuilder,StringBuffer引言 String,StringBuffer,StringBuilder,char[],用来表示字符串。 I 预备知识 1.1 Object类 是所有类的根类 toString…...

2023美赛D题:可持续发展目标
以下内容全部来自人工翻译,仅供参考。 文章目录背景要求术语表文献服务背景 联合国制定了17个可持续发展目标(SDGs)。实现这些目标最终将改善世界上许多人的生活。这些目标并不相互独立,因此,一些目标的积极进展常常…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...
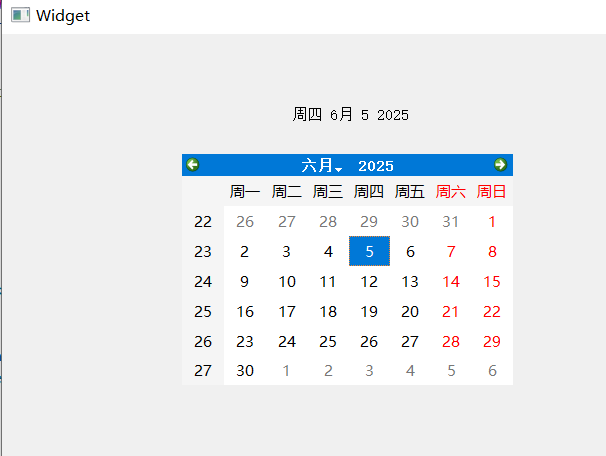
【QT控件】显示类控件
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏:QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...

深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀”
深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀” 在JavaScript中,我们经常需要处理文本、数组、对象等数据类型。但当我们需要处理文件上传、图像处理、网络通信等场景时,单纯依赖字符串或数组就显得力不从心了。这时ÿ…...

【中间件】Web服务、消息队列、缓存与微服务治理:Nginx、Kafka、Redis、Nacos 详解
Nginx 是什么:高性能的HTTP和反向代理Web服务器。怎么用:通过配置文件定义代理规则、负载均衡、静态资源服务等。为什么用:提升Web服务性能、高并发处理、负载均衡和反向代理。优缺点:轻量高效,但动态处理能力较弱&am…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术点解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术点解析 第一轮:基础概念问题 请解释Spring框架的核心容器是什么?它的作用是什么? 程序员JY回答:Spring框架的核心容器是IoC容器(控制反转…...
