无人机影像配准并发布(共线方程)
无人机影像 + DEM 计算四个角点坐标(刚性变换)
-
像空间坐标(x,y,-f)
-
像空间坐标畸变纠正 deltax,deltay

-
已知(x,y),求解(X,Y, Z)或者(Lat,Lon)
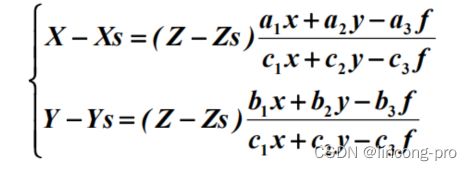
这里的Z是DEM上获取的坐标和Zs为相机坐标的高程,如果均为已知的情况下,则可以求解(X,Y),这里的(X,Y,Z)为地固地心坐标,单位为米。平地的情况只需要获取行高即可求解(X,Y),接着使用proj库将地固地心坐标转化为经纬度坐标即可。 -
地理配准
这里直接采用**gdal_translate和gdal_wrap**,gdal_translate转换过程如下,大概就是将jpg进行地理配准。请注意,GDAL的影像起点是左上角,但是我们的相机模型是左下角,所以需要变换Y轴。转换之后的tif只有专业的QGIS之类的软件才能读取。

下面是QGIS读取的效果。但是为了geoserver能够识别,还需要转换,这时候需要
gdal_wrap,这个时候就很关键,我们需要设置其为透明。gdalwarp -r cubic -ovr AUTO -dstalpha D:\code\roadProj\public\demo\DSC00002\test.tif D:\code\roadProj\public\demo\DSC00002\test3_geotiff.tif
gdal_translate.exe -of GTiff -gcp 0 5304 102.1265090139 29.6453703982 -gcp 7952 5304 102.1164515460 29.6474820822 -gcp 7952 0 102.1131839750 29.6445496193 -gcp 0 0 102.1233217949 29.6424804051 -ovr AUTO -co GCPs_Creation=YES D:\code\roadProj\public\demo\DSC00002\DSC00002.jpg D:\code\roadProj\public\demo\DSC00002\test.tif- geoserver发布,具体操作比较简单
代码逻辑
下面是求解影像四个角点经纬度的简单思路,主要还是共线方程,代码中的1000还是得根据距离地面的高度,即需要DEM的高程值才能求解得到较为精确的精度。
具体实现分为相机模型(固定的参数不部分),大疆无人机是WGS84椭球,EPSG:4978是地心地固的转换参数。
struct CameraModel {double f = 7538.508; // 像素为单位double u0 = 3982.417; // 像素为单位double v0 = 2671.637;double pixelSize = 4.5e-6; // 米为单位double k1 = 2.470920e-9; // 径向畸变系数double k2 = -2.767172e-16;double k3 = 2.479935e-23;double k4 = -6.583598e-31;double p1 = 1.388595e-8; // 偏心畸变系数double p2 = 1.781812e-7;double alpha = -4.697031e-4; // CCD非正方形比例系数double beta = -1.300023e-4;double width = 7952; // 影像的高度和宽度double height = 5304;
};``````cpp
///
/// \brief The ComputeBoundingBox class
/// 计算影像的包围盒的经纬度坐标 + 高程,然后贴地
///
class ComputeBoundingBox {
public:ComputeBoundingBox() {transTool.init("EPSG:4326","EPSG:4978"); // 椭球坐标->地心坐标 XYZ}////// \brief resetR/// \param phi 俯仰角/// \param omega 横滚角/// \param kappa 旋转角///void resetR(double phi, double omega, double kappa) {this->phi = degreeToRadian(phi);this->omega = degreeToRadian(omega);this->kappa = degreeToRadian(kappa);}////// \brief resetCamera/// \param lat 维度/// \param lon 经度/// \param height 高程///void resetCamera(const QString &imgNumber, double lat, double lon, double height) {this->imgNumber = imgNumber;this->cameraLat = lat;this->cameraLon = lon;this->height = height;}////// \brief compute 计算相机位置 + 旋转矩阵///void compute();private:////// \brief computeLatlon 根据像点坐标计算经纬度坐标(共线方程的逻辑)/// @param vector2d uv x轴,y轴坐标///Eigen::Vector2d computeLatlon(Eigen::Vector2d &uv);////// \brief degreeToRadian 度转弧度/// \param degree/// \return///double degreeToRadian(double degree) { return degree * M_PI / 180.0; }// double computeDeltaX();// double computeDeltaY();Eigen::Vector3d cameraGeo;Eigen::Matrix3d rMatrix;Transform transTool;CameraModel intrinsic; // 内参数矩阵QString imgNumber; // 影像编号double cameraLat; // 相机外参数矩阵double cameraLon;double height;double phi;double omega;double kappa;
};
Eigen::Vector2d ComputeBoundingBox::computeLatlon(Eigen::Vector2d &uv) {double u = uv.x();double v = uv.y();Eigen::Vector3d cameraSpace(u, v, -this->intrinsic.f); // 像空间坐标double r = qSqrt(pow(u - this->intrinsic.u0, 2) + pow(v - this->intrinsic.v0, 2));// (x-x0) * (k1*r^2 + k2*r^4 + k3*r^6 + k4*r8) + p1*(r^2 + 2*(x-x)^2) + 2p2*(x-x0)(y-y0) + alpha*(x-x0) +// beta*(y-y0)double deltaX = (u - this->intrinsic.u0) * (this->intrinsic.k1 * pow(r, 2) + this->intrinsic.k2 * pow(r, 4) +this->intrinsic.k3 * pow(r, 6) + this->intrinsic.k4 * pow(r, 8)) +this->intrinsic.p1 * (pow(r, 2) + 2 * pow((u - this->intrinsic.u0), 2)) +2 * this->intrinsic.p2 * (u - this->intrinsic.u0) * (v - this->intrinsic.v0) +this->intrinsic.alpha * (u - this->intrinsic.u0) + this->intrinsic.beta * (v - this->intrinsic.v0);double deltaY = (v - this->intrinsic.v0) * (this->intrinsic.k1 * pow(r, 2) + this->intrinsic.k2 * pow(r, 4) +this->intrinsic.k3 * pow(r, 6) + this->intrinsic.k4 * pow(r, 8)) +this->intrinsic.p2 * (pow(r, 2) + 2 * pow((v - this->intrinsic.v0), 2)) +2 * this->intrinsic.p1 * (u - this->intrinsic.u0) * (v - this->intrinsic.v0);Eigen::Vector3d cameraOffset(deltaX - this->intrinsic.u0, deltaY - this->intrinsic.v0,0); // 像点坐标偏移Eigen::Vector3d cameraSpaceTrue = cameraSpace + cameraOffset; // 实际的像点坐标[最后一位该如何求解]Eigen::Vector3d worldCoordBa =this->rMatrix * cameraSpaceTrue * this->intrinsic.pixelSize; // (xBa, yBa, zBa) pixelSize这个参数多余worldCoordBa =Eigen::Vector3d(worldCoordBa.x() / worldCoordBa.z() * 1000, worldCoordBa.y() / worldCoordBa.z() * 1000, 0);// qDebug() << worldCoordBa.x() << " " << worldCoordBa.y() << " " << worldCoordBa.z();Eigen::Vector3d worldCoord = worldCoordBa + this->cameraGeo; // 真正的坐标// std::cout << worldCoord.x() << " " << worldCoord.y() << " " << worldCoord.z();// PJ_COORD latlonh = proj_coord(cameraLon, cameraLat, height, 0);PJ_COORD geoxyz = proj_coord(worldCoord.x(), worldCoord.y(), worldCoord.z(), 0); // 地心坐标PJ_COORD latlon = this->transTool.backward(geoxyz);// std::cout << "lat:" << latlon.lpz.lam << " ,lon:" << latlon.lpz.phi << ", " << latlon.lpz.z;return Eigen::Vector2d(latlon.lp.phi, latlon.lp.lam); // lat and lon
}
void ComputeBoundingBox::compute() {PJ_COORD latlonh = proj_coord(cameraLon, cameraLat, height, 0);PJ_COORD geoxyz = transTool.forward(latlonh);this->cameraGeo = Eigen::Vector3d(geoxyz.xyz.x, geoxyz.xyz.y, geoxyz.xyz.z); // 地心坐标// 计算绕X轴旋转的旋转矩阵 Rx(φ)Eigen::Matrix3d Rx;Rx << 1, 0, 0, 0, std::cos(phi), -std::sin(phi), 0, std::sin(phi), std::cos(phi);// 计算绕Y轴旋转的旋转矩阵 Ry(ω)Eigen::Matrix3d Ry;Ry << std::cos(omega), 0, std::sin(omega), 0, 1, 0, -std::sin(omega), 0, std::cos(omega);// 计算绕Z轴旋转的旋转矩阵 Rz(κ)Eigen::Matrix3d Rz;Rz << std::cos(kappa), -std::sin(kappa), 0, std::sin(kappa), std::cos(kappa), 0, 0, 0, 1;// 计算总的旋转矩阵 R_total = Rz(κ) * Ry(ω) * Rx(φ)this->rMatrix = Rz * Ry * Rx;// 像素点畸变纠正Eigen::Vector2d lb(0, 0); // 左下角为起点Eigen::Vector2d rb(this->intrinsic.width, 0); // 右下角坐标Eigen::Vector2d rt(this->intrinsic.width, this->intrinsic.height); // 右上角坐标Eigen::Vector2d lt(0, this->intrinsic.height); // 左上角成果std::vector<Eigen::Vector2d> latlonVec = {lb, rb, rt, lt};qDebug() << "####################" << this->imgNumber << "########################";for (Eigen::Vector2d &pixelCoord : latlonVec) {pixelCoord = this->computeLatlon(pixelCoord);qDebug() << "lat: " << QString::number(pixelCoord.x(), 'f', 10)<< ",lon:" << QString::number(pixelCoord.y(), 'f', 10);}
}
效果图

相关文章:

无人机影像配准并发布(共线方程)
无人机影像 DEM 计算四个角点坐标(刚性变换) 像空间坐标(x,y,-f) 像空间坐标畸变纠正 deltax,deltay 已知(x,y),求解(X,Y, Z)或者(Lat,Lon) 这里的Z是DEM上获取的坐标和Zs为相机坐标的高程,如果均为已…...

openGauss学习笔记-23 openGauss 简单数据管理-时间/日期函数和操作符
文章目录 openGauss学习笔记-23 openGauss 简单数据管理-时间/日期函数和操作符23.1 时间日期操作符23.2 时间/日期函数23.3 TIMESTAMPDIFF23.4 EXTRACT23.5 date_part openGauss学习笔记-23 openGauss 简单数据管理-时间/日期函数和操作符 23.1 时间日期操作符 用户在使用时…...
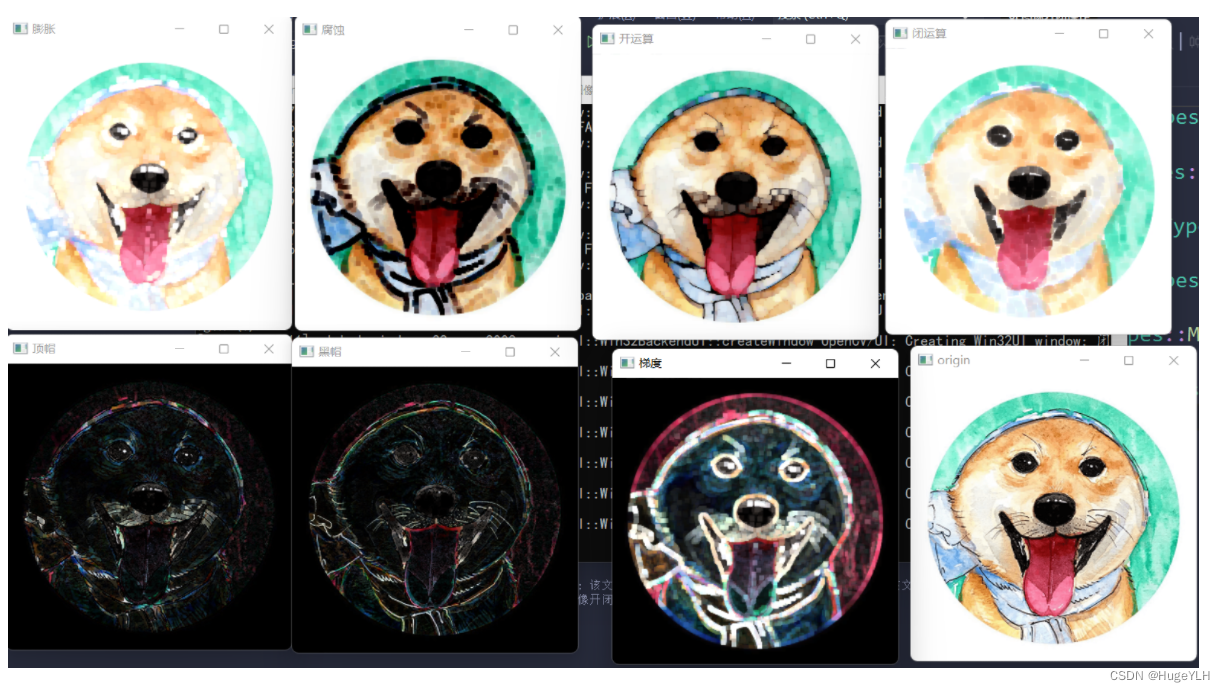
C++OpenCV(7):图像形态学基础操作
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 🔆 OpenCV项目地址及源代码:点击这里 文章目录 膨胀与腐蚀形态学基础 膨胀与腐蚀 膨胀与腐蚀是数学形态学在图像处理中最基础的操作。 膨胀操作是取每个位置领域内最大值࿰…...

Appium+python自动化(二十二)- 控件坐标获取(超详解)
简介 有些小伙伴或者是童鞋可能会好奇会问上一篇中的那个monkey脚本里的坐标点是如何获取的,不是自己随便蒙的猜的,或者是自己用目光或者是尺子量出来的吧,答案当然是:NO。获取控件坐标点的方式这里宏哥给小伙伴们分享和讲解三种方…...
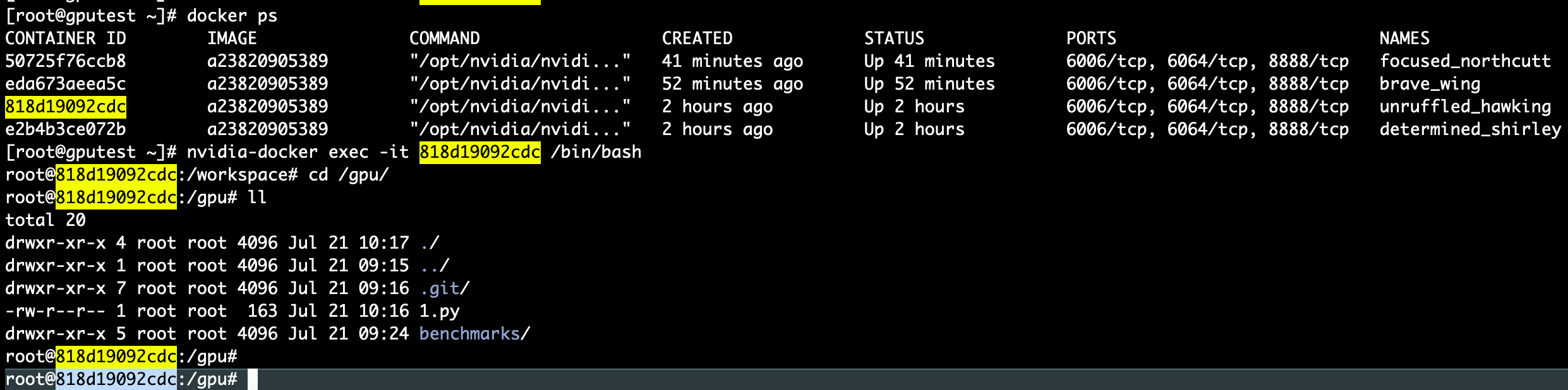
Tensorflow benchmark 实操指南
环境搭建篇见环境搭建-CentOS7下Nvidia Docker容器基于TensorFlow1.15测试GPU_东方狱兔的博客-CSDN博客 1. 下载Benchmarks源码 从 TensorFlow 的 Github 仓库上下载 TensorFlow Benchmarks,可以通过以下命令来下载 https://github.com/tensorflow/benchmarks 我…...

【linux】调试工具介绍
文章目录 前言一、kdb二、ftrace三、gdb 前言 在Linux内核调试过程中,可以使用各种工具和技术来诊断和解决问题。以下是一些常用的Linux内核调试方法: printk:printk是Linux内核中的打印函数,可以在代码中插入打印语句来输出调试…...

2.获取DOM元素
获取DOM元素就是利用JS选择页面中的标签元素 2.1 根据CSS选择器来获取DOM元素(重点) 2.1.1选择匹配的第一个元素 语法: document.querySelector( css选择器 )参数: 包含一个或多个有效的CSS选择器 字符串 返回值: CSS选择器匹配的第一个元素,一个HTMLElement对象…...

flask中redirect、url_for、endpoint介绍
flask中redirect、url_for、endpoint介绍 redirect 在 Flask 中,redirect() 是一个非常有用的函数,可以使服务器发送一个HTTP响应,指示客户端(通常是浏览器)自动导航到新的 URL。基本上,它是用来重定向用…...

《MySQL》第十二篇 数据类型
目录 一. 整数类型二. 浮点类型三. 日期和时间类型四. 字符串类型五. 枚举值类型六. 二进制类型七. 小结 MySQL 支持多种数据类型,学习好数据类型,才能更好的学习 MySQL 表的设计,让表的设计更加合理。 一. 整数类型 类型大小SIGNED(有符号)…...

Python与OpenCV环境中,借助SIFT、单应性、KNN以及Ransac技术进行实现的图像拼接算法详细解析及应用
一、引言 在当今数字化时代,图像处理技术的重要性不言而喻。它在无人驾驶、计算机视觉、人脸识别等领域发挥着关键作用。作为图像处理的一个重要部分,图像拼接算法是实现广阔视野图像的重要手段。今天我们将会讲解在Python和OpenCV环境下,如何使用SIFT、单应性、KNN以及Ran…...

苍穹外卖Day01项目日志
1.软件开发流程和人员分工是怎样的? 软件开发流程 一个软件是怎么被开发出来的? 需求分析 先得知道软件定位人群、用户群体、有什么功能、要实现什么效果等。 需要得到需求规格说明书、产品原型。 需求规格说明书 其中前后端工程师要关注的就是产品原…...
)
Netty学习(二)
文章目录 二. Netty 入门1. 概述1.1 Netty 是什么?1.2 Netty 的作者1.3 Netty 的地位1.4 Netty 的优势 2. Hello World2.1 目标加入依赖 2.2 服务器端2.3 客户端2.4 流程梳理课堂示例服务端客户端 分析提示(重要) 3. 组件3.1 EventLoop事件循…...

ReactRouterv5在BrowserRouter和HashRouter模式下对location.state的支持
结论:HashRouter不支持location.state 文档:ReactRouter v5 从文档可看到history.push()方法支持2个参数:path, [state] state即是location.state,常用于隐式地传递状态参数 但文档未提的是,仅适用于BrowserRouter&am…...
运动设置命令Motion Setup Commands)
Aerotech系列文章(3)运动设置命令Motion Setup Commands
1.运动设置命令Motion Setup Commands 斜坡类型: 直线,S曲线,与正弦曲线 Enumerator: RAMPTYPE_Linear Linear-based ramp type. RAMPTYPE_Scurve S-curve-based ramp type. RAMPTYPE_Sine Sine-based ramp type. 函数原型&a…...

线性神经网络——softmax 回归随笔【深度学习】【PyTorch】【d2l】
文章目录 3.2、softmax 回归3.2.1、softmax运算3.2.2、交叉熵损失函数3.2.3、PyTorch 从零实现 softmax 回归3.2.4、简单实现 softmax 回归 3.2、softmax 回归 3.2.1、softmax运算 softmax 函数是一种常用的激活函数,用于将实数向量转换为概率分布向量。它在多类别…...
【Nodejs】Node.js开发环境安装
1.版本介绍 在命令窗口中输入 node -v 可以查看版本 0.x 完全不技术 ES64.x 部分支持 ES6 特性5.x 部分支持ES6特性(比4.x多些),属于过渡产品,现在来说应该没有什么理由去用这个了6.x 支持98%的 ES6 特性8.x 支持 ES6 特性 2.No…...
简介及Python实现)
梅尔频谱(Mel spectrum)简介及Python实现
梅尔频谱(Mel spectrum)简介及Python实现 1. 梅尔频谱(Mel spectrum)简介2. Python可视化测试3.频谱可视化3.1 Mel 频谱可视化3.2 STFT spectrum参考文献资料1. 梅尔频谱(Mel spectrum)简介 在信号处理上,声信号(噪声信号)是一种重要的传感监测手段。对于语音分类任务…...

【数据结构】实验六:队列
实验六 队列 一、实验目的与要求 1)熟悉C/C语言(或其他编程语言)的集成开发环境; 2)通过本实验加深对队列的理解,熟悉基本操作; 3) 结合具体的问题分析算法时间复杂度。 二、…...

【Linux线程】第一章||理解线程概念+创建一个线程(附代码加讲解)
线程概念 🌵什么是线程🌲线程和进程的关系🎄线程有以下特点:🌳 线程的优点🌴 线程的缺点🌱线程异常🌿线程用途 ☘️手动创建一个进程🍀运行 🌵什么是线程 在L…...

Android进阶之微信扫码登录
遇到新需求要搭建微信扫码登录功能,这篇文章是随着我的编码过程一并写的,希望能够帮助有需求的人和以后再次用到此功能的自己。 首先想到的就是百度各种文章,当然去开发者平台申请AppID和密钥是必不可少的,等注册好发现需要创建应用以及审核(要官网,流程图及其他信息),想着先写…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
