el-tree转换为表格样式的记录2
上一篇文章记录的是自己将树状数据转换为表格形式。但是出现了一个小bug,点击子节点时候会选中父节点,这个是正常需求没问题。但是我点击父节点时候取消所有子节点,父节点 选择也会失去,这是我不想要执行的。例如一个页面里面有主页,各种小组件,但是我只想看一个主页,小组件都不要了。而不是我如果想要看主页必须最少选择一个组件。
代码:
el-tree的组件方法
| check-change | 节点选中状态发生变化时的回调 | 共三个参数,依次为:传递给 data 属性的数组中该节点所对应的对象、节点本身是否被选中、节点的子树中是否有被选中的节点 |
| check | 当复选框被点击的时候触发 | 共两个参数,依次为:传递给 data 属性的数组中该节点所对应的对象、树目前的选中状态对象,包含 checkedNodes、checkedKeys、halfCheckedNodes、halfCheckedKeys 四个属性 |
<el-treeshow-checkbox:data="allMenu":default-expand-all="true"node-key="permissionId"ref="menuTree"check-strictlyhighlight-current:props="xxxxx"empty-text="暂未匹配到信息"@check="handleCheck"@check-change="handleCheckChange"></el-tree>一、递归调用获取所有的节点ID
| setChecked | 通过 key / data 设置某个节点的勾选状态,使用此方法必须设置 node-key 属性 | (key/data, checked, deep) 接收三个参数,1. 勾选节点的 key 或者 data 2. boolean 类型,节点是否选中 3. boolean 类型,是否设置子节点 ,默认为 false |
这里为什么不使用带S的。肯定是这个方法有问题。
| setCheckedKeys | 通过 keys 设置目前勾选的节点,使用此方法必须设置 node-key 属性 | (keys, leafOnly) 接收两个参数,1. 勾选节点的 key 的数组 2. boolean 类型的参数,若为 |
selectChildren(data) {if (data && data.sonPermissionList) {// 如果数据存在且有子权限列表data.sonPermissionList.map((item) => {// 将子节点的权限设置为勾选状态this.$refs.menuTree.setChecked(item.permissionId, true);if (data.sonPermissionList) {// 如果子权限列表存在,则递归调用 selectChildren 方法this.selectChildren(item);}});}
}二,点击复选框事件
在点击时候能获取到当前的树目前的选中状态对象,包含 checkedNodes、checkedKeys、halfCheckedNodes、halfCheckedKeys 四个属性
handleCheck(data, { checkedKeys }) {// 第二个参数使用解构赋值获取选中状态的对象 checkedKeys// 使用 includes 方法判断当前节点的权限ID是否包含在 checkedKeys 中。如果包含,则调用 selectChildren 方法。if (checkedKeys.includes(data.permissionId)) {this.selectChildren(data);}
},三、在点击复选框时候 进行父子节点的处理
handleCheckChange(data, checked, indeterminate) {if (checked === false) {if (data.sonPermissionList) {// 如果当前节点被取消勾选data.sonPermissionList.map((item) => {// 将子节点的权限设置为取消勾选状态this.$refs.menuTree.setChecked(item.permissionId, false);});}} else {if (data.pid !== null) {// 如果当前节点被勾选,并且有父节点this.$refs.menuTree.setChecked(data.pid, true);}}// 获取勾选状态的节点数组var check = this.$refs.menuTree.getCheckedNodes();// 提取节点数组中的权限ID,并去重var idList = check.map((item) => {this.permissionIdList = [];return item.permissionId;});this.permissionIdList.push(...idList);// 对去重后的权限ID列表进行过滤this.permissionIdList = this.permissionIdList.filter((item, index) => {return this.permissionIdList.indexOf(item, 0) === index;});
}相关文章:

el-tree转换为表格样式的记录2
上一篇文章记录的是自己将树状数据转换为表格形式。但是出现了一个小bug,点击子节点时候会选中父节点,这个是正常需求没问题。但是我点击父节点时候取消所有子节点,父节点 选择也会失去,这是我不想要执行的。例如一个页面里面有主…...

MS1826B HDMI 1进4出 视频拼接芯片
MS1826B 是一款多功能视频处理器,包含 4 路独立 HDMI 音视频输出通道、1 路 HDMI 音视 频输入通道以及 1 路独立可配置为输入或者输出的 SPDIF、I2S 音频信号。支持 4 个独立的字库定 制型 OSD;可处理隔行和逐行视频或者图形输入信号;有四路独…...

Spring之注解
SpringIOC注解 组件添加标记注解: Component:该注解标记类表示该类为一个普通类,表示为IOC中的一个组件bean Repository:该注解用于将数据访问层(Dao层)的类标识为Spring中的Bean Service&…...

【UniApp开发小程序】悬浮按钮+出售闲置商品+商品分类选择【基于若依管理系统开发】
文章目录 界面效果界面实现悬浮按钮实现商品分类选择界面使元素均匀分布 闲置商品描述信息填写界面价格校验 界面效果 【悬浮按钮】 【闲置商品描述信息填写界面】 【商品分类选择界面】 【分类选择完成】 界面实现 悬浮按钮实现 悬浮按钮漂浮于页面之上,等页面…...
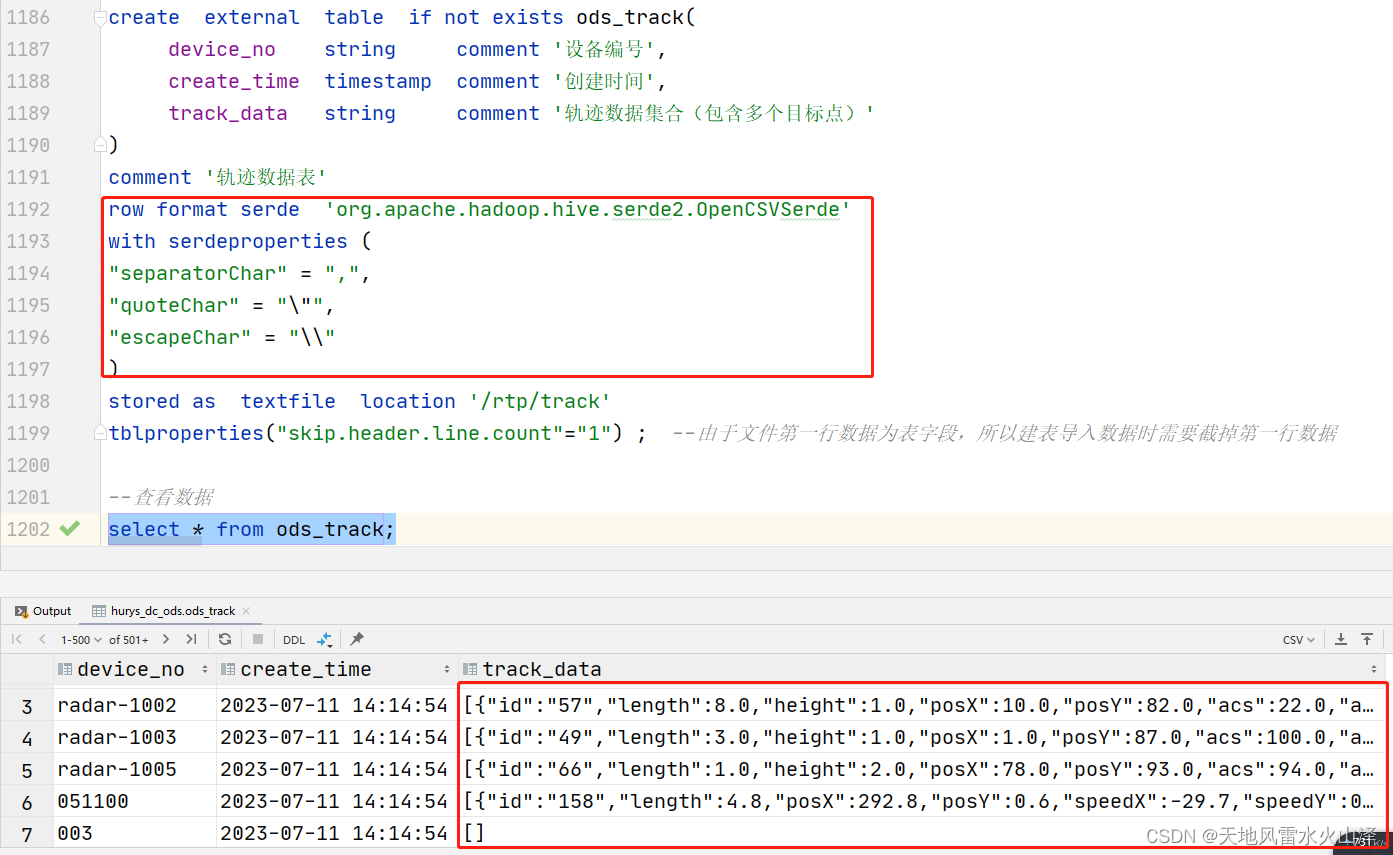
一百三十三、Hive——Hive外部表加载含有JSON格式字段的CSV文件数据
一、目标 在Hive的ODS层建外部表,然后加载HDFS中的CSV文件数据 注意:CSV文件中含有未解析的JSON格式的字段数据,并且JSON字段中还有逗号 二、第一次建外部表,直接以,分隔行字段,结果JSON数据只显示一部分…...
rust gtk 桌面应用 demo
《精通Rust》里介绍了 GTK框架的开发,这篇博客记录并扩展一下。rust 可以用于桌面应用开发,我还挺惊讶的,大学的时候也有学习过 VC,对桌面编程一直都很感兴趣,而且一直有一种妄念,总觉得自己能开发一款很好…...
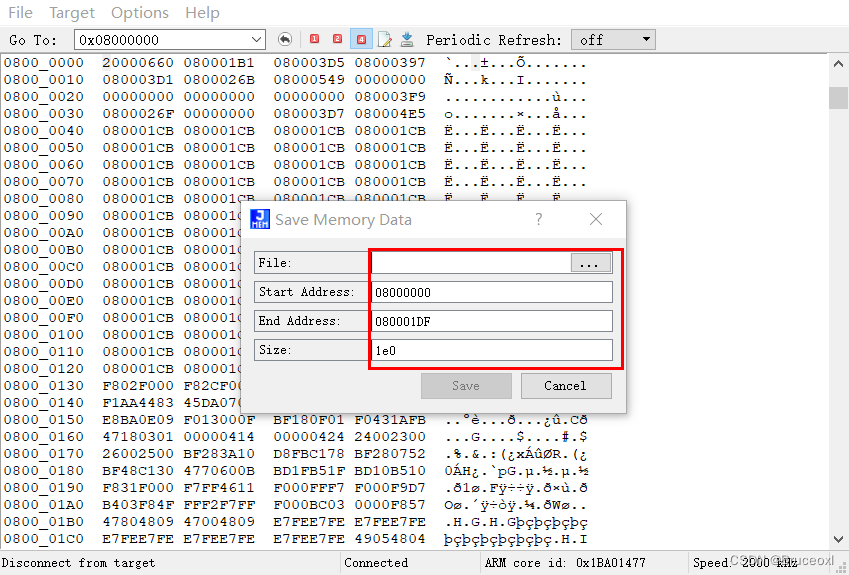
《嵌入式 - 工具》J-link读写MCU内部Flash
1 J-Link简介 J-Link是SEGGER公司为支持仿真ARM内核芯片推出的JTAG仿真器。配合IAR EWAR,ADS,KEIL,WINARM,RealView等集成开发环境支持所有ARM7/ARM9/ARM11,Cortex M0/M1/M3/M4, Cortex A5/A8/A9等内核芯片的仿真,是学…...

算法练习-LeetCode1071. Greatest Common Divisor of Strings
题目地址:LeetCode - The Worlds Leading Online Programming Learning Platform Description: For two strings s and t, we say "t divides s" if and only if s t ... t (i.e., t is concatenated with itself one or more times). Given two strin…...

Nuget不小心用sudo下载后怎么在user里使用
问题发生 协同开发的过程中,同时在dotnet里面添加了nuget的grpc包,在不清楚的情况下执行自动生成脚本,下载nuget包失败,说是权限不足,于是就使用了sudo进行自动生成,结果在下一次重新打包的过程中ÿ…...

软件测试技能大赛环境搭建及系统部署报告
环境搭建及系统部署报告 环境搭建与配置过程(附图) JDK环境变量配置截图 【截取JDK环境变量配置截图】 查看JDK版本信息截图 【截取使用命令查看JDK版本信息截图,必须截取查看信息成功截图】 root账号成功登录MySQL截图 【截取使用root账…...

浅谈现代通信技术
目录 1.传统通信方法 2.传统通信方式的缺点 3.现代通信技术 4.现代通信技术给人类带来的福利 1.传统通信方法 传统通信方法指的是在数字化通信之前使用的传统的通信方式。以下是一些常见的传统通信方法: 1. 书信:通过邮件或快递等方式发送纸质信件。这…...
windows环境下adb 下载和配置,连接手机。
ADB下载地址: https://adbdownload.com/ 选择下载windows系统的。 下载后解压,查看adb.exe所在的目录,如下 这里将路径复制下来:D:\ADB 配置到系统环境变量中。 然后再打开cmd,输入adb version查看版本。 出现…...

[STL]list使用介绍
[STL]list使用 注:本文测试环境是visual studio2019。 文章目录 [STL]list使用1. list介绍2. 构造函数3. 迭代器相关函数begin函数和end函数rbegin函数和rend函数 4. 容量相关函数empty函数size函数 5. 数据修改函数push_back函数和pop_back函数push_front函数和pop…...

k8s服务发现之第五弹--使用 Service 连接到应用
Kubernetes 的网络模型 通过前面教程的学习,我们已经可以将容器化的应用程序在 Kubernetes 中运行起来,并且发布到 Kubernetes 内/外的网络上。 通常,Docker 使用一种 host-private 的联网方式,在此情况下,只有两个容…...

SAP ABAP 自定义表数据导入
一:效果展示: 读取 Excel 数据到 SAP 数据库表。 二:源码: *&---------------------------------------------------------------------* *& Report ZTEST_DRW02 *&----------------------------------------------------------…...

目标检测识别——大恒(DaHeng)相机操作与控制编程
文章目录 引言正文相关开发库的介绍编程准备配置引用头文件GalaxyIncludes.h配置lib文件 具体编程过程初始化和反初始化枚举设备开关设备 属性控制属性控制器种类 图像采集控制和图像处理采单帧回调采集 总结 引言 在做老师的横向项目时,需要用大恒相机,…...
国标GB28181视频监控平台EasyGBS视频无法播放,抓包返回ICMP是什么原因?
国标GB28181视频平台EasyGBS是基于国标GB/T28181协议的行业内安防视频流媒体能力平台,可实现的视频功能包括:实时监控直播、录像、检索与回看、语音对讲、云存储、告警、平台级联等功能。国标GB28181视频监控平台部署简单、可拓展性强,支持将…...

如何正确使用npm常用命令
npm常用命令: 官方文档:CLI Commands | npm Docs 1. npm -v:查看 npm 版本 2. npm init:初始化后会出现一个 Package.json 配置文件,可以在后面加上 -y,快速跳到问答界面 3. npm install:会…...

无人机影像配准并发布(共线方程)
无人机影像 DEM 计算四个角点坐标(刚性变换) 像空间坐标(x,y,-f) 像空间坐标畸变纠正 deltax,deltay 已知(x,y),求解(X,Y, Z)或者(Lat,Lon) 这里的Z是DEM上获取的坐标和Zs为相机坐标的高程,如果均为已…...

openGauss学习笔记-23 openGauss 简单数据管理-时间/日期函数和操作符
文章目录 openGauss学习笔记-23 openGauss 简单数据管理-时间/日期函数和操作符23.1 时间日期操作符23.2 时间/日期函数23.3 TIMESTAMPDIFF23.4 EXTRACT23.5 date_part openGauss学习笔记-23 openGauss 简单数据管理-时间/日期函数和操作符 23.1 时间日期操作符 用户在使用时…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
