SDK命令行工具配置
SDK命令行工具配置
最早的Android SDK工具包,包含一些GUI的工具。
而在一些场景(如打包)只需要命令行工具时,下载 command-line tools 即可。
到 Android Studio下载页 ,找到 Command line tools only 下载。
命令行工具包,替换了原SDK工具包 tools 目录下的内容:
- sdkmanager 查看、更新、安装、卸载SDK包
- avdmanager 创建Android虚拟设备,即模拟器命令
- apkanalyzer 分析APK
- lint 扫描分析代码
- retrace
1. 配置方法
通过下载页,得到最新下载地址(这里使用了Linux平台的):
https://dl.google.com/android/repository/commandlinetools-linux-9477386_latest.zip
通过一下方法配置:
- 创建Android SDK目录,可命名为 android_sdk
- 把下载的命令行工具解压
- 把解压cmdline-tools目录下内容,移动到 android_sdk/cmdline-tools/latest 目录下
完成配置,通过 android_sdk/cmdline-tools/latest/bin/sdkmanager 来更新下载SDK工具包。
2. sdkmanager
负责SDK的管理。
# 列出所有可用的包
sdkmanager --list# 安装包,可以安装多个用空格分开
sdkmanager "platforms;android-33" "build-tools;34.0.0"# 安装CMake或NDK,使用下面语法
sdkmanager --install "ndk;21.3.6528147"
sdkmanager --install "cmake;10.24988404"# 卸载包
sdkmanager --uninstall "platforms;android-33"# 更新已安装的包
sdkmanager --update# 接受协议
sdkmanager --licenses
3. SDK一键配置脚本
上面所述配置,这里提供 完成下载初始化目录、安装sdk相关包 的 Shell脚本:
#!/bin/shSDK_DIR=./android_sdk
# 配置命令行工具目录
mkdir -p $SDK_DIR/cmdline-tools/latest
wget https://dl.google.com/android/repository/commandlinetools-linux-9477386_latest.zip
unzip -o commandlinetools-linux-9477386_latest.ziprm -rf $SDK_DIR/cmdline-tools/latest/*
mv -f cmdline-tools/* $SDK_DIR/cmdline-tools/latest# 接受协议,安装sdk
cd $SDK_DIR/cmdline-tools/latest/bin
yes | ./sdkmanager --licenses
./sdkmanager "platforms;android-32" "build-tools;34.0.0"
文档
- 命令行工具 https://developer.android.com/tools#tools-sdk
- sdkmanager https://developer.android.com/tools/sdkmanager
- 旧的sdk-tools下载和配置 https://blog.csdn.net/lkl22/article/details/77225096
- 参考博客 Linux下命令行安装配置android sdk
相关文章:

SDK命令行工具配置
SDK命令行工具配置 最早的Android SDK工具包,包含一些GUI的工具。 而在一些场景(如打包)只需要命令行工具时,下载 command-line tools 即可。 到 Android Studio下载页 ,找到 Command line tools only 下载。 命令…...
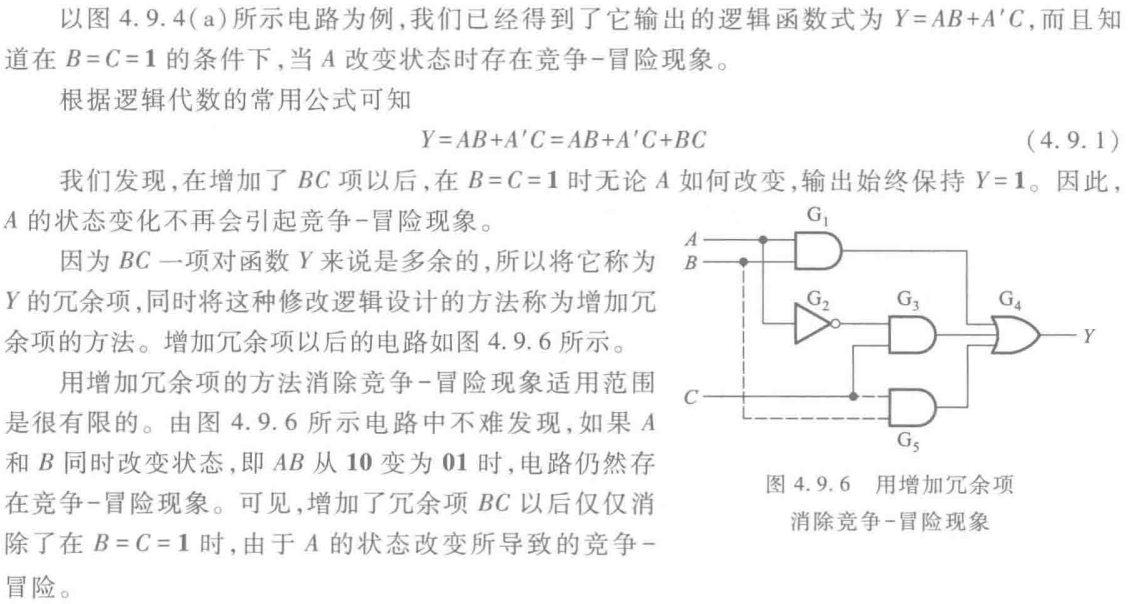
【数字IC基础】竞争与冒险
竞争-冒险 1. 基本概念2. 冒险的分类3. 静态冒险产生的判断4. 毛刺的消除使用同步电路使用格雷码增加滤波电容增加冗余项,消除逻辑冒险引入选通脉冲 1. 基本概念 示例一: 如上图所示的这个电路,使用了两个逻辑门,一个非门和一个与…...
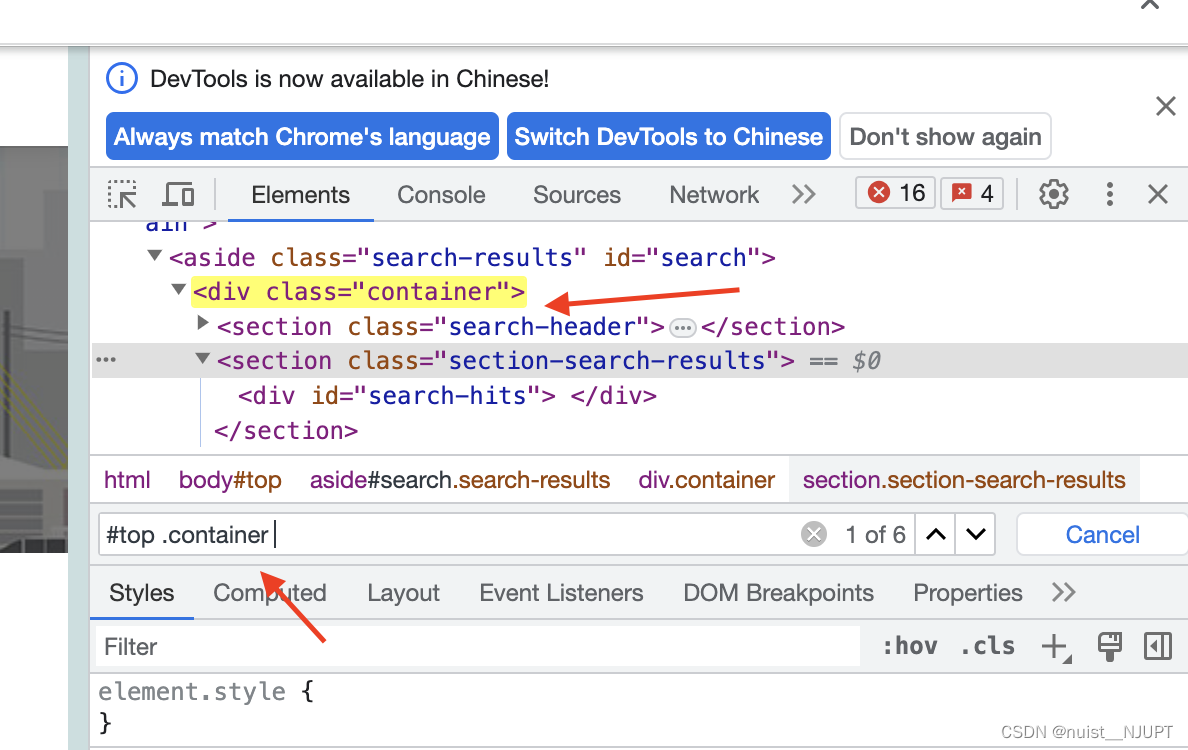
速成版-带您一天学完python自动化测试(selenium)
Selenium是一套web网站的程序自动化操作解决方案。我们通过编写自动化程序,使得自动完成浏览器界面的相关操作,除了能够自动化的完成相关操作,还能从web页面获取相关信息,然后通过程序进行分析处理,本质上就是提升从网…...
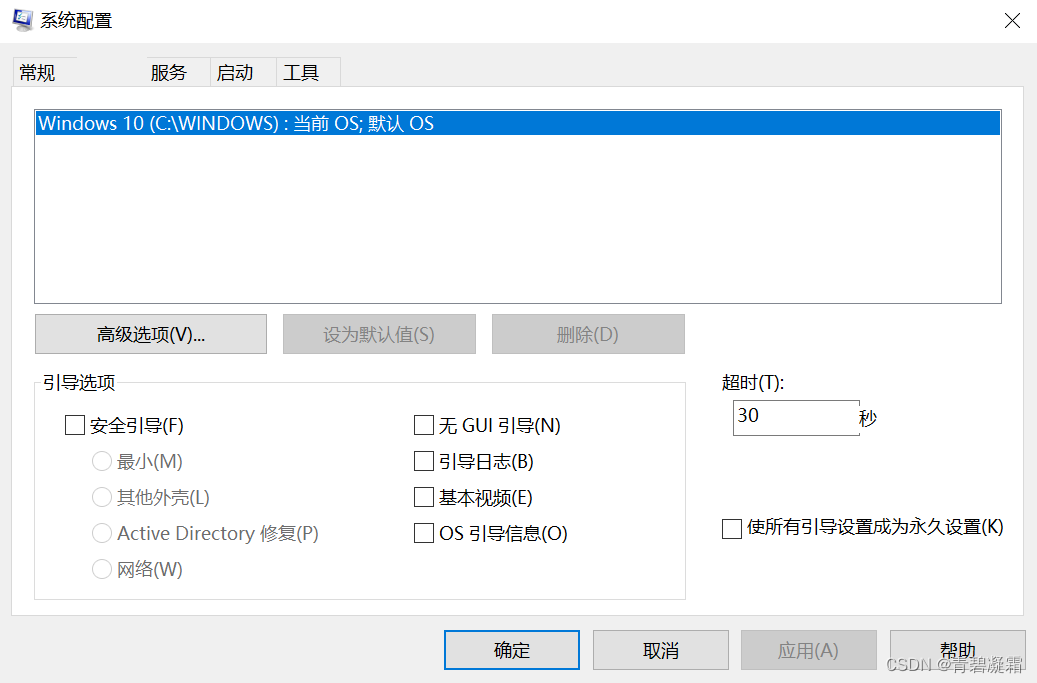
windows 删除无法删除的文件
有两种原因: 文件被占用文件无权限 解决方案 通用解决方案是进入安全模式进行删除 安全模式: 不会启动非必要的进程有最高的系统权限 进入系统配置 安全引导,重启 删除文件 修改系统配置为正常启动 重启...

FFmpeg[7] - FFmpeg之预设编码参数preset
目录 前言 正文 一、定义与作用 二、取值范围 三、枚举值 四、使用实例...

CVPR2023新作:3D视频物体检测
Title: 3D Video Object Detection With Learnable Object-Centric Global Optimization Affiliation: 中国科学院自动化研究所 (Institute of Automation, Chinese Academy of Sciences),中国科学院大学人工智能学院 (School of Artificial Intelligence, Univers…...

Keepalived热备、Keepalived+LVS、HAProxy监控及后端服务器健康检查、负载均衡调度器对比
day02 day02KeepAlived高可用集群配置高可用的web集群监控本机80端口,实现主备切换实现原理实施配置高可用、负载均衡的web集群配置高可用、负载均衡HAProxy配置haproxy负载均衡调度器比较LVS(Linux Virtual Server)NginxHAProxy KeepAlive…...
)
用Vue开发仿旅游站webapp项目总结 (上)
写着写着发现会写不少内容... 全部写在一篇文章里感觉太多了不方便看,所以分为上下篇吧... 下篇写完啦,感兴趣的朋友可以继续关注~ > 用Vue开发仿旅游站webapp项目总结 (下) 温馨提示 此文章,仅是做完项目后的个人…...
【Koa】[NoSQL] Koa中相关介绍和使用Redis MongoDB增删改查
目录 NoSQL非关系型数据库关系型数据库(RMDB)介绍非关系型数据库(NoSQL)介绍Redis & MongoDB 在 Koa 中使用 Redis (了解)Redis 的安装和使用在 Koa 中连接 和 调用 Redis 在 Koa 中使用 MongoDBMongoDB 的安装MongoShell 操作…...

【JS 阻止滑动穿透】
在实现阻止滑动穿透时,可以使用以下方法之一: 使用 CSS 属性 overflow: hidden 来禁止页面滚动。 body {overflow: hidden; }使用 JavaScript 监听滚动事件并阻止默认行为。 document.addEventListener(touchmove, function(e) {e.preventDefault(); …...

编译原理
目录 一,基本概念 二,词法分析 三,自上而下推导 一,基本概念 二,词法分析 三,自上而下推导...

项目播报 | 新基德携手璞华易研PLM,打造企业新一代研发管理平台
近日,“新基德PLM(Product Lifecycle Management,产品生命周期管理)项目”在新基德(深圳)电子有限公司(以下简称:新基德)正式启动。新基德是一家集手机研发、生产、销售、…...

elementui el-table 封装表格
ps: 1.3版本 案例: 完整代码: 可直接复制粘贴,但一定要全看完! v-slot"scopeRows" 是vue3的写法; vue2是 slot-scope"scope" <template><!-- 简单表格、多层表头、页码、没有合并列行…...

集合--collections
一、collections概述 Collections和Arrays、Objects-一样,都是一种针对性的工具类, Arrays是针对数组,Objects是针对Object, 而Colections则是针对集合的一种工具类,里面提供了大量的方便我们操作集合的方法: //往集合中添加一些元素。 p…...

go使用gin结合jwt做登录功能
1、安装gin go get -u github.com/gin-gonic/gin 2、安装session go get github.com/gin-contrib/sessions 3、安装JWT鉴权 go get "github.com/golang-jwt/jwt/v4" 4、创建一个jwt的工具文件 package utilsimport ("errors""github.com/golan…...

【C++】开源:Boost网络库Asio配置使用
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍Asio网络库配置使用。 无专精则不能成,无涉猎则不能通。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,下次…...
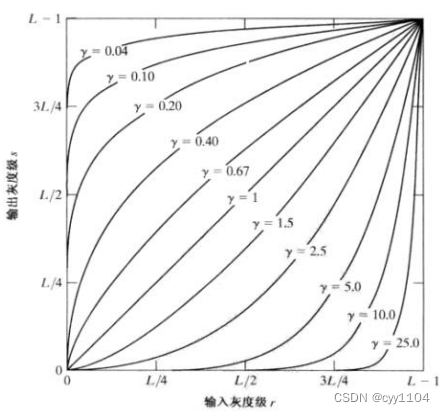
图像滤波器
图像噪声 • 图像噪声是图像在获取或是传输过程中受到随机信号干扰,妨碍人们对图像理解及分析处理 的信号。 • 图像噪声的产生来自图像获取中的环境条件和传感元器件自身的质量,图像在传输过程中产 生图像噪声的主要因素是所用的传输信道受到了噪声…...

【每日一题】2569. 更新数组后处理求和查询
【每日一题】2569. 更新数组后处理求和查询 2569. 更新数组后处理求和查询题目描述解题思路 2569. 更新数组后处理求和查询 题目描述 给你两个下标从 0 开始的数组 nums1 和 nums2 ,和一个二维数组 queries 表示一些操作。总共有 3 种类型的操作: 操作…...
PLC的高端版本通常具有以下特点:
高速处理能力:高端PLC通常具有更快的处理速度和更高的运行频率,可以处理更复杂的控制逻辑和更多的输入/输出信号。 大容量存储:高端PLC通常具有更大的存储容量,可以保存更多的程序和数据,以满足更复杂的应用需求。 多种…...

Scrum敏捷开发项目管理和产品研发管理培训- Leangoo领歌
Scrum是目前运用最为广泛的敏捷开发方法,是一个轻量级的项目管理和产品研发管理框架。 这是一个两天的实训课程,面向研发管理者、项目经理、产品经理、研发团队等,旨在帮助学员全面系统地学习Scrum和敏捷开发, 帮助企业快速启动敏捷实施。 …...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
