HCIP——OSPF的防环机制
OSPF的防环机制
- 一、域间防环
- 二、域内防环
- 有向图转化
- 1、有向图的画法
- 2、示例:
- 三、SPF算法
OSPF将整个OSPF域划分为多个区域,区域内部通过拓扑信息计算路由,区域间传递路由信息,实现全网可达。OSPF防环机制主要是体现在域内防环和域间防环。
一、域间防环
-
OSPF的星型拓扑划分规则实际上就是一种防环手段。OSPF要求所有的非0区域必须与骨干区域直接相连,区域间路由需经由骨干区域中转。OSPF要求所有的非0区域必须与骨干区域直接相连, 区域间( Inter- - Area Route )路由需经由骨干区域中转。这个要求使得区域间的路由传递不能发生在两个非0的区域之间,这在很大程度上规避了区域间路由环路的发生,也使得OSPF的区域架构在逻辑上形成了一个类似星型的拓扑,如下图所示。

-
ABR从非骨干区域收到的Type-3 LSA不能用于区域间路由的计算。当一台 ABR 在非 Area0 的区域中收到 Type- - 3 LSA 时,虽然它会将其装载进 LSDB ,但是该路由器不会使用这些 Type- - 3 LSA 进行路由计算,当然它更不会将这些 Type- - 3 LSA 再注入回Area0 中。

-
区域之间存在水平分割机制,从某个区域学到的路由信息不会再通告到这个区域,这和距离适量协议的水平分割相似,区域水平分割可以概括为:从此区域出,不进此区域。

二、域内防环
OSPF基于一类二类LSA的洪泛收集区域内的拓扑信息,将这些拓扑信息转化为有向图,再用SPF算法将有向图转化为最短路径树,而树形结构是无环的,OSPF最后依据树形结构将路由加载到路由表中。
有向图转化
一类LSA描述了某个设备的接口信息,二类LSA只是一类LSA对MA网络的补充,通过查看一二类LSA可以画出单区域的有向图。
1、有向图的画法
- 一类LSA中有四种接口类型,这里我们不考虑virtual类型
| Type | Link ID | Data |
|---|---|---|
| p-2-p | 邻居的RID | 该网段上本地接口的IP地址 |
| TransNet | DR的接口的IP地址 | 该网段上本地接口的IP地址 |
| StubNet | 该Stub网段的IP网络地址 | 该网段的网路掩码 |
| Virtual | 虚连接邻居的RID | 去往该虚连接的本地接口IP |
- Stub网段表示该网段只有数据入口,例如一个Loopback接口就是一个Stub网段。转化为有向图时路由器为一个圈,stub网段也是一个圈,然后再画一条路由器指向stub网段的箭头,箭头上添上该接口的开销值,表示路由器到该网段的需要的开销值。
描述拓扑结构——路由器节点和Stub网段

- Transit网段即一个MA网段,从路由器到所连Transit网段的开销值就是连接到这个网段的接口所配
置的开销值。从一个Transit网段到连接到这个网段的路由器的开销为0。下图的N1也被称为伪节点。
描述拓扑结构——Transit网段

在描述点到点接口的Router-LSA中:
1、通告一个到邻居路由器的点到点链接,Link ID设置为对端的Router
ID,Data设置为本地接口的IP地址;
2、 通告一个到该点到点网段的Stub连接,Link ID设置为该点到点网段
的网络号,Data设置为该点到点网段的网络掩码;
3、上述两个连接的Cost值均为该点到点接口上的Cost值。
- 一类LSA在描述p2p网络时,由于点到点链路两端接口的网络号可能不一致,所以需要有两个link对其描述。
- 两接口处于不同网段的点到点网段的规则如下:两台路由器经由两条有向线段直接相连,每个方向一条。两个接口的网段被表示成Stub网段。每个路由器通告一个Stub连接到该路由器所连的网段
描述拓扑结构——点对点网段

- 两接口处于同一网段的点到点网段的规则如下:两台路由器经由两条有向线段直接相连,每个方向一条。连接两个接口的网段被表示成Stub网段。
描述点对点网段

2、示例:
计算最短路径树——物理拓扑

由LSDB描述的有向图

三、SPF算法
SPF算法每一个路由器都将自己作为根(ROOT)来计算其到每一个目的地路由器的距离,每一个路由器根据一个统一的数据库会计算出路由域的拓扑结构图,该结构图类似于一棵树,在SPF算法中,被称为最短路径树。OSPF计算阶段分为两个阶段:
| 第一阶段 | 计算Transit节点,忽略Stub节点,生成一个最短路径树 |
|---|---|
| 第二阶段 | 只计算Stub节点,将Stub网段挂到最短路径树上去 |
计算过程中首先初始化最短路径树,RTA将自己做为根节点添加到最短路径树上

- RTA将自己添加到最短路径树上之后,检查自己生成的Router-LSA,对于该LSA中所描述的每一个连接,如果不是一个Stub连接,就把该连接添加到候选列表中,端点ID为Link ID,到根端点的开销为LSA中描述的Metric值。本例中,添加端点4.4.4.4和2.2.2.2。

- 将候选列表中到根端点开销最小的端点移到最短路径树上


- 当有新节点添加到最短路径树上的时候,则检查LS ID为新节点的link-idID的LSA,本例中检查LS ID为2.2.2.2的LSA。
如果LSA中所描述的连接的Link ID在最短路径树上已经存在,则忽略该连接。本例中,Link ID为1.1.1.1的连接被忽略,只有10.3.1.1的连接被添加到候选列表中。到根端点的开销设置为此连接的Metric值(本例中此连接的Metric值为1)与父端点(本例中此连接的父端点为2.2.2.2)到根端点的开销(本例中此开销值为48)之和。

将候选列表中到根端点的开销最小的端点移动到最短路径树上,本例中,将10.3.1.1移到最短路径树上。


- 检查LS ID为最新添加节点的端点ID的LSA,本例中检查LS ID为10.3.1.1的LSA。
在所描述的连接中,忽略2.2.2.2,将3.3.3.3和4.4.4.4添加到候选列表中。从Transit网段到所连路由器的开销为0。如果在候选列表中出现两个端点ID一样但是到根端点的开销不一样的端点,则删除到根端点的开销大的端点。

将候选列表中到根端点的开销最小的端点移动到最短路径树上,本例中,将3.3.3.3移到最短路径树上。


- 检查LS ID为最新添加节点的端点ID的LSA,本例中检查LS ID为3.3.3.3的LSA。
本例中,没有新端点被添加到候选列表中。

- 将候选列表中到根端点的开销最小的端点移动到最短路径树上,本例中,将4.4.4.4移到最短路径树上。


- 检查LS ID为最新添加节点的端点ID的LSA,本例中检查LS ID为4.4.4.4的LSA。
本例中,没有新端点被添加到候选列表中。如果在此时候选列表为空,则计算最短路径树的第一阶段结束。

- 检查每个路由器端点的Router-LSA,计算Stub网段。
本例中,首先检查RTA的Router-LSA,共有三个Stub网段。




相关文章:

HCIP——OSPF的防环机制
OSPF的防环机制 一、域间防环二、域内防环有向图转化1、有向图的画法2、示例: 三、SPF算法 OSPF将整个OSPF域划分为多个区域,区域内部通过拓扑信息计算路由,区域间传递路由信息,实现全网可达。OSPF防环机制主要是体现在域内防环和…...

安全基础 --- 正则表达式
正则表达式是表达文本模式的方法 正则表达式(Regular Expression),简称为正则或Regex,是一个用来描述、匹配和操作字符串的工具。 (1)限定字符 限定字符多用于重复匹配次数 常用限定字符: 语…...

【vue】vue面试高频问题之-$nextTick的作用和使用场景
nextTick的作用和使用场景 vue中的nextTick主要用于处理数据动态变化后,DOM还未及时更新的问题,用nextTick就可以获取数据更新后最新DOM的变化 api文档 Vue.nextTick( [callback, context] ) 参数: {Function} [callback]{Object} [context]…...

MySQL学习笔记之SQL语句执行过程查看
文章目录 参数使能查看最近一条SQL执行过程查看profiling打开开后,所有SQL语句执行耗时查看某一条SQL的执行过程指定要查看的性能选项查看所有性能选项 参数使能 以select语句为例,首先打开profile参数: mysql> set profiling 1; Query…...
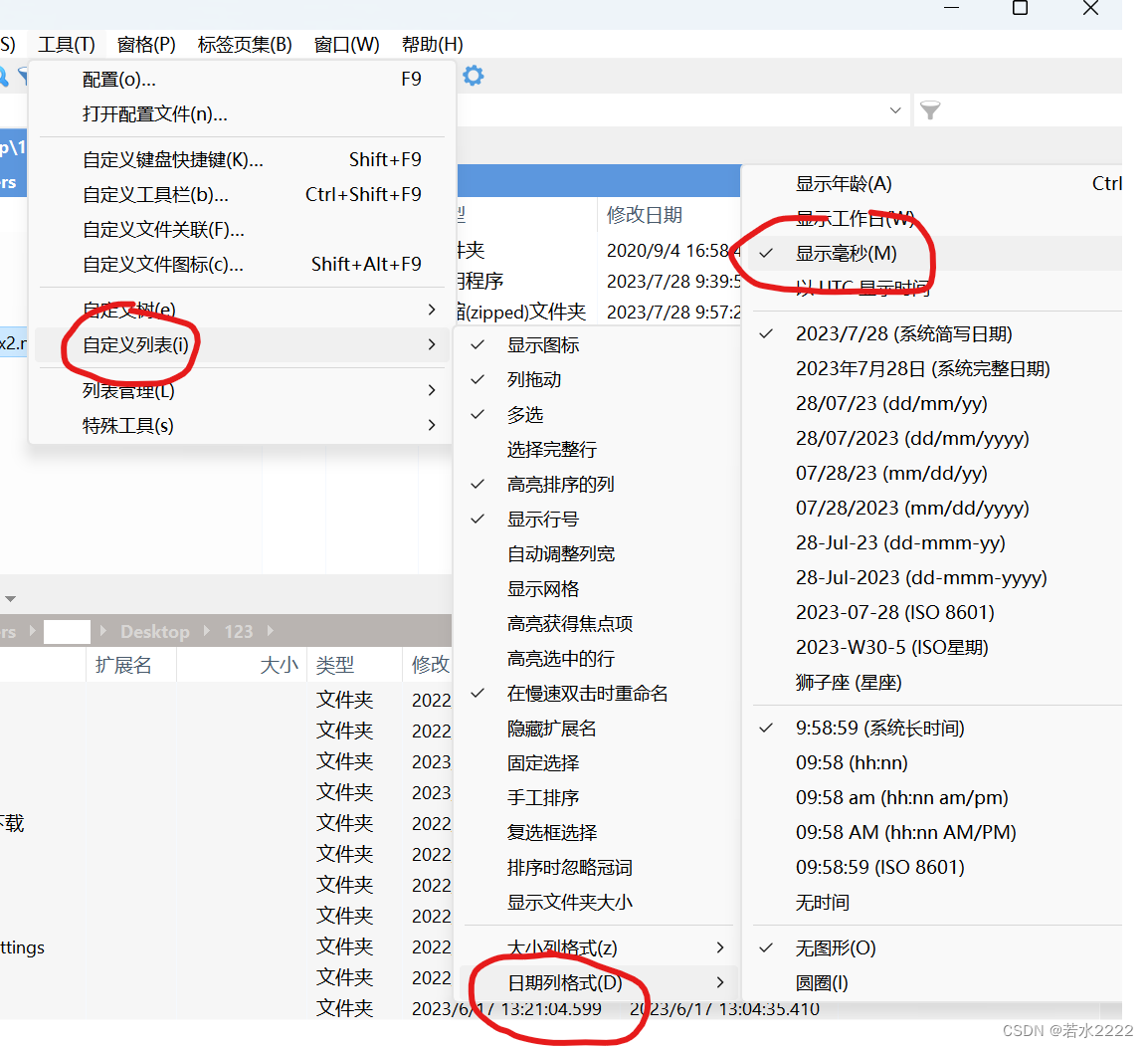
如何以毫秒精度,查看系统时间以及文件的创建时间
用 cmd 查看系统的时间: powershell -command "(Get-Date -UFormat %Y-%m-%d %H:%M:%S).toString() . ((Get-Date).millisecond)" 用 XYplorer 查看文件的精确创建时间(含30天试用): XYplorer - File Manager for …...
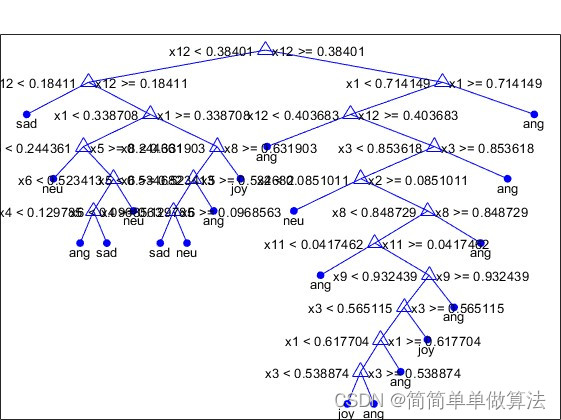
基于机器学习的情绪识别算法matlab仿真,对比SVM,LDA以及决策树
目录 1.算法理论概述 2.部分核心程序 3.算法运行软件版本 4.算法运行效果图预览 5.算法完整程序工程 1.算法理论概述 情绪识别是一种重要的情感分析任务,旨在从文本、语音或图像等数据中识别出人的情绪状态,如高兴、悲伤、愤怒等。本文介绍一种基于…...
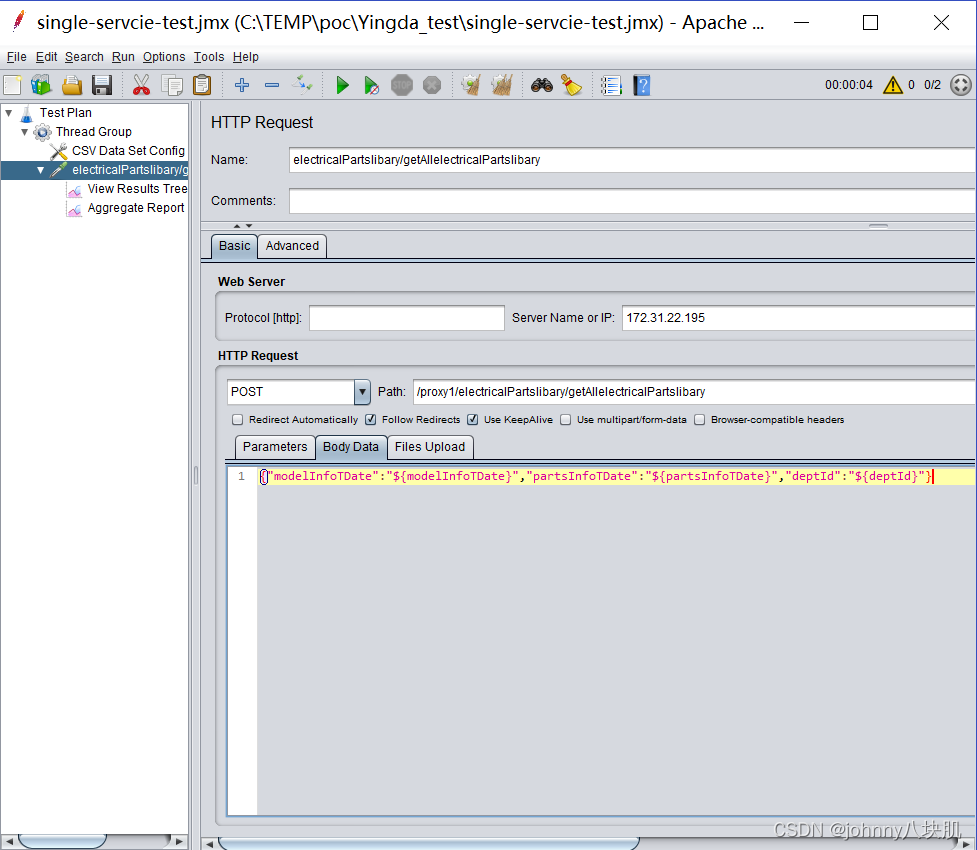
jMeter使用随记
参数化BodyData 先制作参数文件 再设置一个csv data set config 最后在body data里面写上参数${xxxxx}...

[语义分割] DeepLab v3(Cascaded model、ASPP model、两种ASPP对比、Multi-grid、训练细节)
Rethinking Atrous Convolution for Semantic Image Segmentation 论文地址:Rethinking Atrous Convolution for Semantic Image SegmentationPytorch 实现代码:pytorch_segmentation/deeplab_v3 这是一篇 2017 年发表在CVPR上的文章。相比 DeepLab V2 有…...

css - Media Query
使用bootstrap的grid system可以在一个较为粗糙的范围得到较好的响应性,但是通过viewport可以看到网站在具体哪个像素点处变得丑陋,再通过css media query来精细调整网页布局。 可以通过media query来提高网页移动响应能力。...
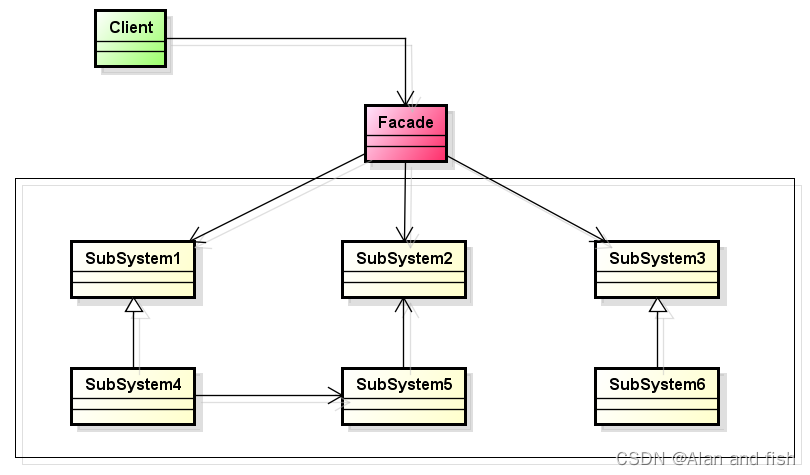
9.python设计模式【外观模式】
内容:为子系统中的一组接口提供一个一致的界面,外观模式定义了一个高层接口,这个接口使得这一个子系统更加容易使用。 角色: 外观(facade)子类系统(subsystem classes) UML图 举…...

Webpack5 CopyPlugin的作用
在Webpack 5中,CopyPlugin是一个插件,用于将文件或目录从源位置复制到构建目录中。它的作用是帮助开发人员在构建过程中将静态文件(如图片、字体等)直接复制到输出目录,而无需经过任何处理。 CopyPlugin并不是必须的&…...

kafka服务端允许生产者发送最大消息体大小
1、kafka config服务端配置文件server.properties server.properties中加上的message.max.bytes配置,我目前设置为5242880,即5MB,可以根据实际情况增大。 message.max.bytes5242880 在生产者端配置max.request.size,这是单个消息…...

台阶型Nim游戏博弈论
台阶型Nim游戏 题目 https://www.acwing.com/problem/content/894/ 现在,有一个 n n n 级台阶的楼梯,每级台阶上都有若干个石子,其中第 i i i 级台阶上有 a i a_i ai 个石子( i ≥ 1 i \ge 1 i≥1)。 两位玩家轮流操作,每…...

NestJS 的 中间件 学习
基本概念 中间件是在路由处理程序之前调用的函数。中间件函数可以访问请求和响应对象。在程序中我们可以让多个中间件串起来一起使用,当多个中间件一起使用时我们可以使用next()调用下一个中间件。 中间件主要是可以实现如下功能: 执行任何代码更改请…...

搭建自己第一个golang程序
概念: golang 和 java有些类似,配置好环境就可以直接编写运行了;这里分两种: 一.shell模式 创建一个go类型的文件 往里面编写代码 二.开发工具模式 这里的开发工具 我选用goland package mainimport "fmt"func mai…...
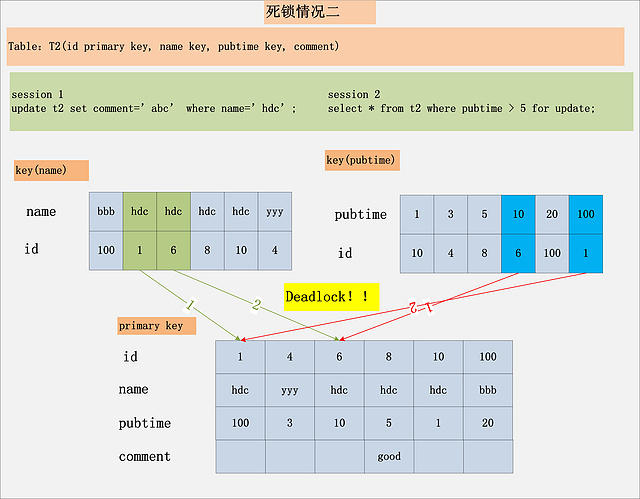
Mysql加锁过程
1、背景 MySQL/InnoDB的加锁分析,一直是一个比较困难的话题。我在工作过程中,经常会有同事咨询这方面的问题。同时,微博上也经常会收到MySQL锁相关的私信,让我帮助解决一些死锁的问题。本文,准备就MySQL/InnoDB的加锁问…...

财经界杂志财经界杂志社财经界编辑部2023年第19期目录
《财经界》投稿邮箱:cnqikantg126.com(注明投稿“《财经界》”) ●崔编辑Q Q :695548262 微信号:f99832970 名刊名著_国内外名刊名著 财经名刊名著 李少鹏 ;王海蕴; 6-7 发改委专线 六方面发力 看中国经济形势,既要看准当…...

Linux常用命令——dpkg-split命令
在线Linux命令查询工具 dpkg-split Debian Linux中将大软件包分割成小包 补充说明 dpkg-split命令用来将Debian Linux中的大软件包分割成小软件包,它还能够将已分割的文件进行合并。 语法 dpkg-split(选项)(参数)选项 -S:设置分割后的每个小文件最…...
常见的二十种软件测试方法详解
一.单元测试(模块测试) 单元测试是对软件组成单元进行测试。其目的是检验软件组成单位的正确性。测试对象是:模块。 对模块进行测试,单独的一个模块测试,属于静态测试的一类 测试阶段:编码后或者编码前&…...

Python(一)
要做到坚韧不拔,最要紧的是坚持到底。——陀思妥耶夫斯基 2023 6 14~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ --根据你自己的操作系统下载对应的。 -- pyhton 文档 --交互方式 使用的工具 --如何启动工具 -- 交互式方式一般在数据分析中…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...
