网络安全/信息安全—学习笔记
一、网络安全是什么
网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。
无论网络、Web、移动、桌面、云等哪个领域,都有攻与防两面性,例如 Web 安全技术,既有 Web 渗透,也有 Web 防御技术(WAF)。作为一个合格的网络安全工程师,应该做到攻守兼备。
二、网络安全的前景
人才需求量很大的,市场空缺大,像物联网网应用的普及、5G的普及等,都会增加网络安全岗位的需求。
从长久来看,网络安全只会越来越火,智能学科的崛起必定带动新型的网络安全技术发展。
网络安全未来三大发展方向:网络安全(安全等保)、云原生安全、 AI 人工智能在网络安全的运用( ChatGPT )
发展空间大:
在企业内部,网络工程师基本处于"双高"地位,即地位高、待遇高。就业面广,一专多能,实践经验适用于各个领域。
增值潜力大:
掌握企业核心网络架构、安全技术,具有不可替代的竞争优势。职业价值随着自身经验的丰富以及项目运作的成熟,升值空间一路看涨。
职业寿命长:
网络工程师工作的重点在于对企业信息化建设和维护,其中包含技术及管理等方面的工作,工作相对稳定,随着项目经验的不断增长和对行业背景的深入了解,会越老越吃香。
最后,我在这里可以很肯定地告诉你:"网络安全有很好的发展前景,前沿网络安全技术即将崛起,或者说已经崛起"。
三、网络安全技能表
【一一帮助安全学习,所有资源一一】
①网络安全学习路线
②20份渗透测试电子书
③安全攻防357页笔记
④50份安全攻防面试指南
⑤安全红队渗透工具包
⑥网络安全必备书籍
⑦100个漏洞实战案例
⑧安全大厂内部视频资源
⑨历年CTF夺旗赛题解析
【——关注自动发送一一】

四、网络安全的知识多而杂,怎么科学合理安排?
如果你已经决定开始学网络安全的话,那建议你看看下面我所说,具体到每个知识点,自学时间共计半年左右,亲测有效(文末有惊喜):
第一阶段:安全基础
网络安全行业与法规
Linux操作系统
计算机网络
HTML PHP Mysql Python基础到实战掌握
第二阶段:信息收集
IP信息收集
域名信息收集
服务器信息收集
Web网站信息收集
Google hacking
Fofa网络安全测绘
第三阶段:Web安全
SQL注入漏洞
XSS
CSRF漏洞
文件上传漏洞
文件包含漏洞
SSRF漏洞
XXE漏洞
远程代码执行漏洞
密码暴力破解与防御
中间件解析漏洞
反序列化漏洞
第四阶段:渗透工具
MSF
Cobalt strike
Burp suite
Nessus Appscea AWVS
Goby XRay
Sqlmap
Nmap
Kali
第五阶段:实战挖洞
漏洞挖掘技巧
Src
Cnvd
众测项目
热门CVE漏洞复现
靶场实战
五、最后
学习框架学习路线已经制定完全,接下来就差资源跟随学习了。
网络平台或者各大论坛都能找到学习资料,但是本人经历是感觉找的资料都是东一块西一块,前言不搭后语,学着学着就懵了,越学越难。
如果你想学的话,我可以把我自己学习的笔记全部分享,全知识点全内容,包含电子书、面试题、pdf文档、视频以及相关的课件笔记,关注后台自动发送。

希望大家都能学成,成为优秀的网络安全工程师!
相关文章:

网络安全/信息安全—学习笔记
一、网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 无论网络、Web、移动、桌面、云等哪个领域,都有攻与防两面…...

【Visual Studio】无法打开包括文件: “dirent.h”: No such file or directory
VS2017/2019 无法打开包括文件: “dirent.h”: No such file or directory 1 “dirent.h”: No such file or directory 在windows下的VS2017/2019编译器中,发现无法打开“dirent.h”,主要是MSVC并没有实现这个头文件,但是在Linux这个头文件…...

asp.net MVC markdown编辑器
在 ASP.NET MVC 中,你可以使用一些第三方 Markdown 编辑器来让用户在网页上方便地编辑和预览 Markdown 内容。这些编辑器通常提供实时预览功能,将 Markdown 文本转换为实时渲染的 HTML,并支持编辑器工具栏来辅助用户编辑。 以下是一些流行的…...

论文浅尝 | 预训练Transformer用于跨领域知识图谱补全
笔记整理:汪俊杰,浙江大学硕士,研究方向为知识图谱 链接:https://arxiv.org/pdf/2303.15682.pdf 动机 传统的直推式(tranductive)或者归纳式(inductive)的知识图谱补全(KGC)模型都关注于域内(in-domain)数据,而比较少关…...
)
算法工程师-机器学习面试题总结(2)
线性回归 线性回归的基本思想是? 线性回归是一种用于建立和预测变量之间线性关系的统计模型。其基本思想是假设自变量(输入)和因变量(输出)之间存在线性关系,通过建立一个线性方程来拟合观测数据ÿ…...

低成本32位单片机空调内风机方案
空调内风机方案主控芯片采用低成本32位单片机MM32SPIN0230,内部集成了具有灵动特色的电机控制功能:高阶4路互补PWM、注入功能的高精度ADC、轨到轨运放、轮询比较器、32位针对霍尔传感器的捕获时钟、以及硬件除法器和DMA等电机算法加速引擎。 该方案具有…...
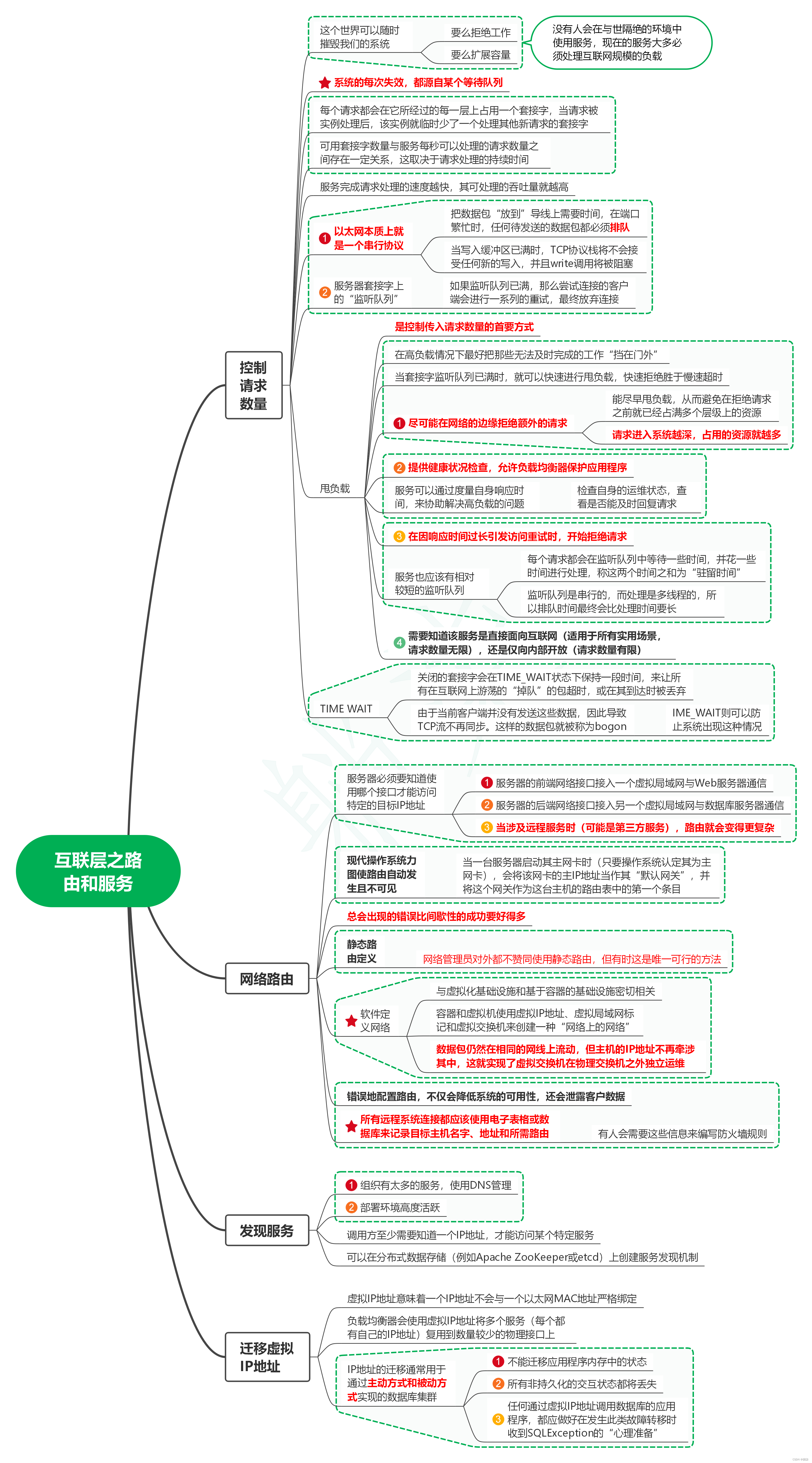
读发布!设计与部署稳定的分布式系统(第2版)笔记25_互联层之路由和服务
1. 控制请求数量 1.1. 这个世界可以随时摧毁我们的系统 1.1.1. 要么拒绝工作 1.1.2. 要么扩展容量 1.1.3. 没有人会在与世隔绝的环境中使用服务,现在的服务大多必须处理互联网规模的负载 1.2. 系统的每次失效,都源自某个等待队列 1.3. 每个请求都会…...
)
AI面试官:LINQ和Lambda表达式(二)
AI面试官:LINQ和Lambda表达式(二) 当面试官面对C#中关于LINQ和Lambda表达式的面试题时,通常会涉及这两个主题的基本概念、用法、实际应用以及与其他相关技术的对比等。以下是一些可能的面试题目,附带简要解答和相关案…...

Mysql原理篇--第二章 索引
文章目录 前言一、mysql的索引是什么?1.1 索引的结构:1.2 b树特性:1.3 b树每个节点的结构:1.4 b树 键值的大小排序:1.4 b树 存储(InnoDB): 二、索引类型2.1 主要的索引类型ÿ…...
保姆级系列教程-玩转Fiddler抓包教程(1)-HTTP和HTTPS基础知识
1.简介 有的小伙伴或者童鞋们可能会好奇地问,不是讲解和分享抓包工具了怎么这里开始讲解HTTP和HTTPS协议了。这是因为你对HTTP协议越了解,你就能越掌握Fiddler的使用方法,反过来你越使用Fiddler,就越能帮助你了解HTTP协议。 Fid…...

【iOS】单例、通知、代理
1 单例模式 1.1 什么是单例 单例模式在整个工程中,相当于一个全局变量,就是不论在哪里需要用到这个类的实例变量,都可以通过单例方法来取得,而且一旦你创建了一个单例类,不论你在多少个界面中初始化调用了这个单例方…...

从Vue2到Vue3【五】——新的组件(Fragment、Teleport、Suspense)
系列文章目录 内容链接从Vue2到Vue3【零】Vue3简介从Vue2到Vue3【一】Composition API(第一章)从Vue2到Vue3【二】Composition API(第二章)从Vue2到Vue3【三】Composition API(第三章)从Vue2到Vue3【四】C…...
PostgreSQL——sql文件导入
Windows方式: 进入PostgreSQL安装目录的bin,进入cmd 执行命令: psql -d 数据库名 -h localhost -p 5432 -U 用户名 -f 文件目录 SQL Shell: 执行命令: \i 文件目录(Windows下要加引号和双斜线)...

[SQL挖掘机] - 全连接: full join
介绍: 在sql中,join是将多个表中的数据按照一定条件进行关联的操作。全连接(full join)是一种连接类型,它会返回所有满足连接条件的行,同时还包括那些在左表和右表中没有匹配行的数据。 在进行全连接时,会…...

SpringDataJpa 实体类—主键生成策略
主键配置 IdGeneratedValue(strategy GenerationType.IDENTITY)Column(name "cust_id")private Long custId;//主键 Id:表示这个注解表示此属性对应数据表中的主键GeneratedValue(strategy GenerationType.IDENTITY) 此注解表示配置主键的生成策…...

【LeetCode 算法】Parallel Courses III 并行课程 III-拓扑
文章目录 Parallel Courses III 并行课程 III问题描述:分析代码拓扑 Tag Parallel Courses III 并行课程 III 问题描述: 给你一个整数 n ,表示有 n 节课,课程编号从 1 到 n 。同时给你一个二维整数数组 relations ,其…...

进行消息撤回功能的测试时,需要考虑哪些?
进行消息撤回功能的测试时,可以考虑以下测试点: 1. 功能可用性测试:确认消息撤回功能是否能够正常使用,并且在不同的场景下(例如单聊、群聊)是否表现一致。 2. 撤回时限测试:检查消息撤回的时…...
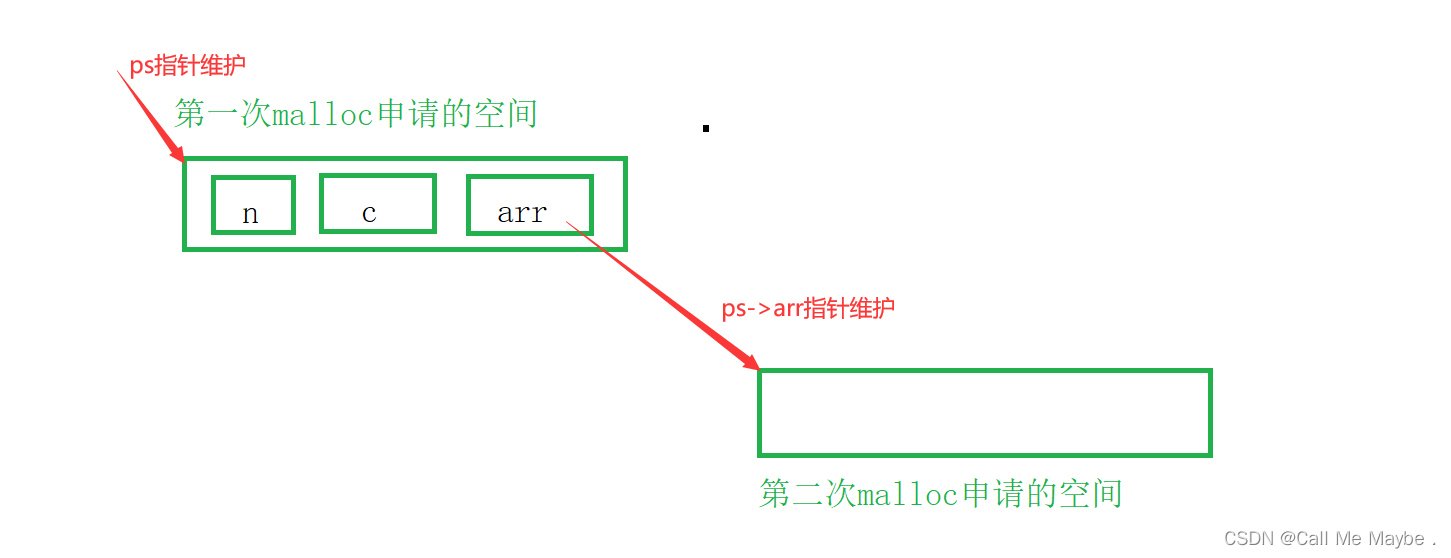
C语言动态内存管理(三)
目录 五、C/C程序的内存开辟1.图解2.关键点 六、柔性数组1.什么是柔性数组2.两种语法形式3.柔性数组的特点4.柔性数组的创建及使用在这个方案中柔性数组的柔性怎么体现出来的? 5.不用柔性数组,实现数组可大可小的思路6.对比 总结 五、C/C程序的内存开辟 1.图解 &a…...
通过cmake工程生成visual studio解决方案
1、前言 visual studio是一个很强大的开发工具,这个工具主要是通过解决方案对我们的源码进行编译等操作。但是我们很多时候拿到的可能并不是一个直接的解决方案,可能是是一个cmake工程,那么这个时候我们就需要通过cmake工程生成解决方案&…...
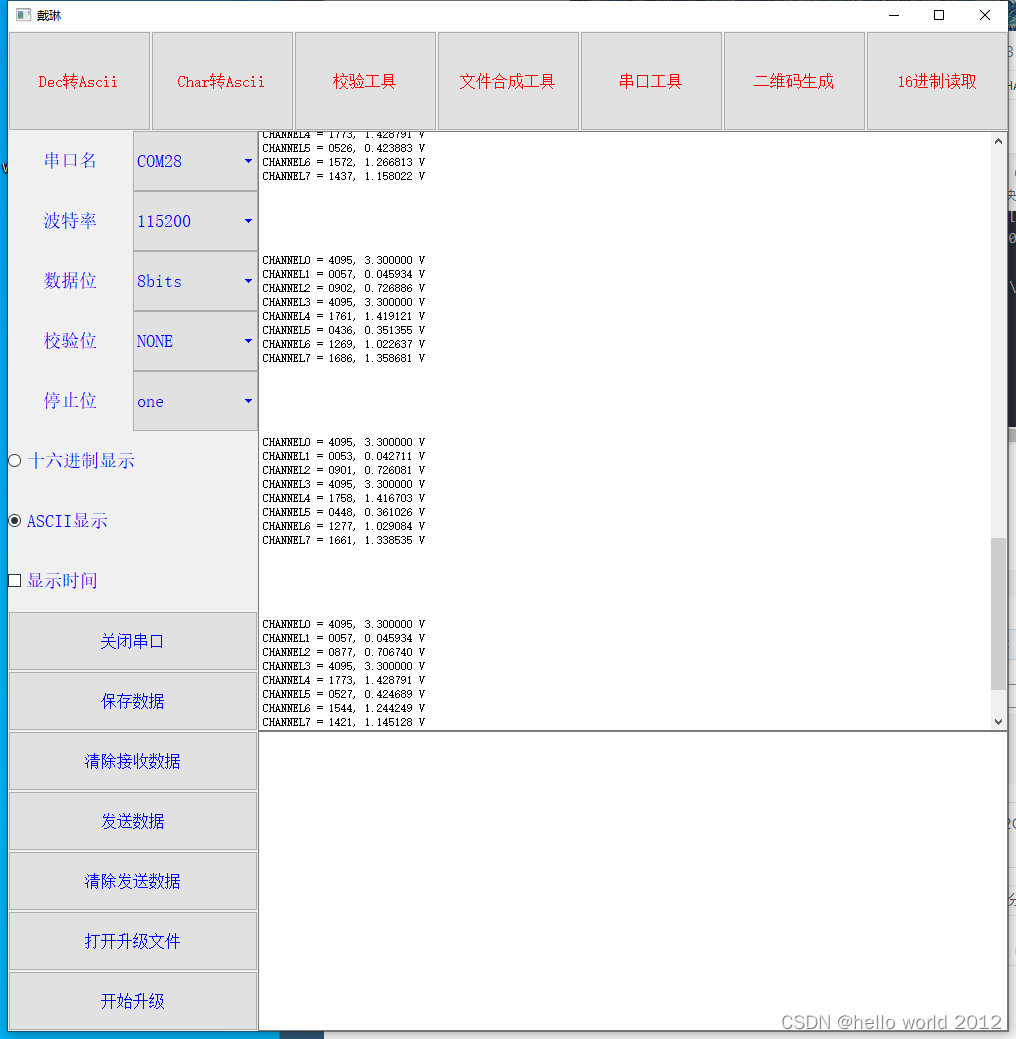
STM32CubeMX配置STM32G031多通道ADC + DMA采集(HAL库开发)
时钟配置HSI主频配置64M 勾选打开8个通道的ADC 使能连续转换模式 添加DMA DMA模式选择循环模式 使能DMA连续请求 采样时间配置160.5 转换次数为8 配置好8次转换的顺序 配置好串口,选择异步模式配置好需要的开发环境并获取代码 修改main.c 串口重定向 #include &…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

Linux入门(十五)安装java安装tomcat安装dotnet安装mysql
安装java yum install java-17-openjdk-devel查找安装地址 update-alternatives --config java设置环境变量 vi /etc/profile #在文档后面追加 JAVA_HOME"通过查找安装地址命令显示的路径" #注意一定要加$PATH不然路径就只剩下新加的路径了,系统很多命…...

OpenGL-什么是软OpenGL/软渲染/软光栅?
软OpenGL(Software OpenGL)或者软渲染指完全通过CPU模拟实现的OpenGL渲染方式(包括几何处理、光栅化、着色等),不依赖GPU硬件加速。这种模式通常性能较低,但兼容性极强,常用于不支持硬件加速…...
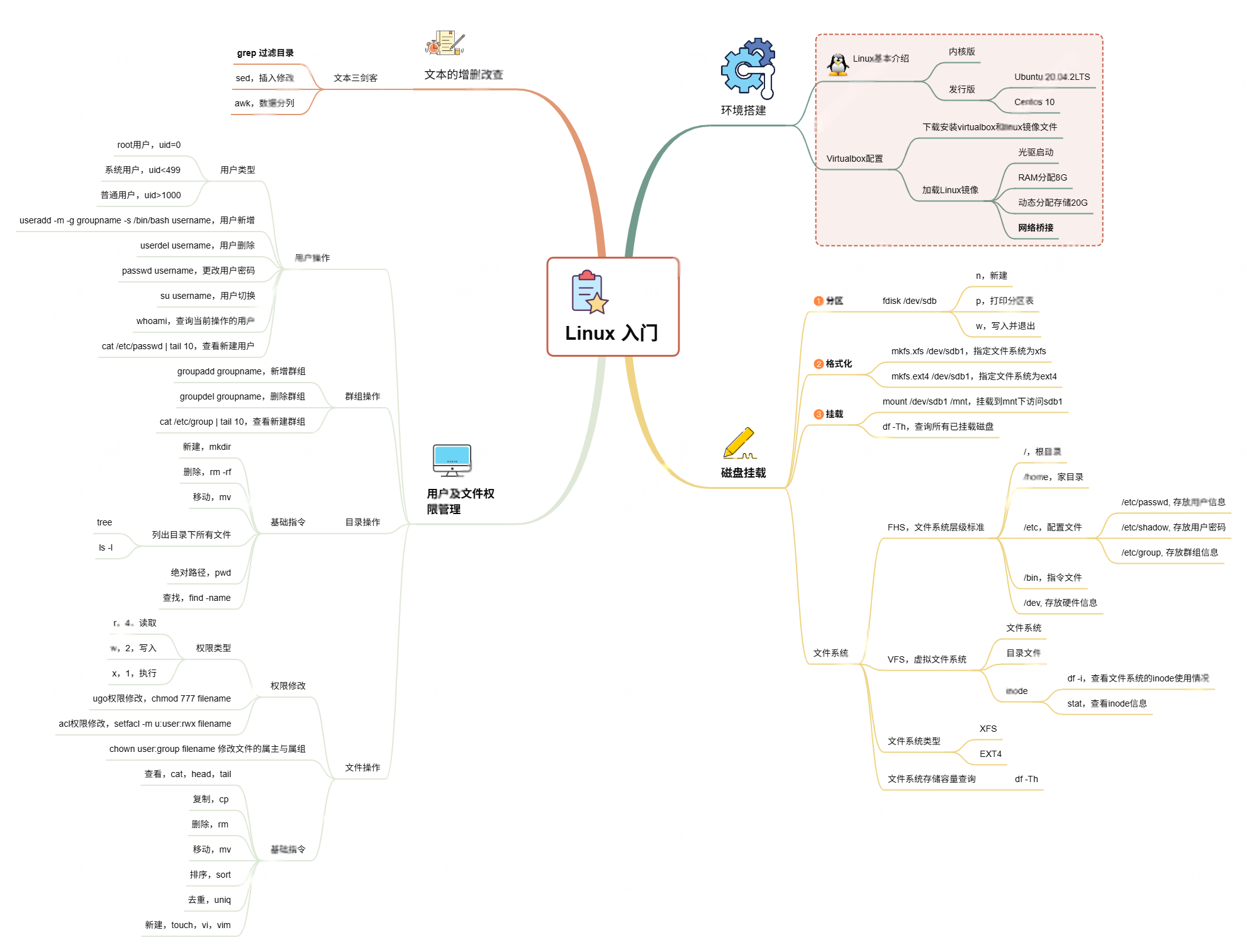
Linux入门课的思维导图
耗时两周,终于把慕课网上的Linux的基础入门课实操、总结完了! 第一次以Blog的形式做学习记录,过程很有意思,但也很耗时。 课程时长5h,涉及到很多专有名词,要去逐个查找,以前接触过的概念因为时…...

比较数据迁移后MySQL数据库和ClickHouse数据仓库中的表
设计一个MySQL数据库和Clickhouse数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
