【LeetCode 算法】Parallel Courses III 并行课程 III-拓扑
Parallel Courses III 并行课程 III
问题描述:
给你一个整数 n ,表示有 n 节课,课程编号从 1 到 n 。同时给你一个二维整数数组 relations ,其中 r e l a t i o n s [ j ] = [ p r e v C o u r s e j , n e x t C o u r s e j ] relations[j] = [prevCourse_j, nextCourse_j] relations[j]=[prevCoursej,nextCoursej] ,表示课程 p r e v C o u r s e j prevCourse_j prevCoursej 必须在课程 n e x t C o u r s e j nextCourse_j nextCoursej 之前 完成(先修课的关系)。同时给你一个下标从 0 开始的整数数组 time ,其中 t i m e [ i ] time[i] time[i] 表示完成第 ( i + 1 ) (i+1) (i+1) 门课程需要花费的 月份 数。
请你根据以下规则算出完成所有课程所需要的 最少 月份数:
如果一门课的所有先修课都已经完成,你可以在 任意 时间开始这门课程。
你可以 同时 上 任意门课程 。
请你返回完成所有课程所需要的 最少 月份数。
注意:测试数据保证一定可以完成所有课程(也就是先修课的关系构成一个有向无环图)。
1 < = n < = 5 ∗ 1 0 4 0 < = r e l a t i o n s . l e n g t h < = m i n ( n ∗ ( n − 1 ) / 2 , 5 ∗ 1 0 4 ) r e l a t i o n s [ j ] . l e n g t h = = 2 1 < = p r e v C o u r s e j , n e x t C o u r s e j < = n p r e v C o u r s e j ! = n e x t C o u r s e j 所有的先修课程对 [ p r e v C o u r s e j , n e x t C o u r s e j ] 都是互不相同的。 t i m e . l e n g t h = = n 1 < = t i m e [ i ] < = 1 0 4 先修课程图是一个有向无环图 1 <= n <= 5 * 10^4\\ 0 <= relations.length <= min(n * (n - 1) / 2, 5 * 10^4)\\ relations[j].length == 2\\ 1 <= prevCourse_j, nextCourse_j <= n\\ prevCourse_j != nextCourse_j\\ 所有的先修课程对 [prevCourse_j, nextCourse_j] 都是 互不相同 的。\\ time.length == n\\ 1 <= time[i] <= 10^4\\ 先修课程图是一个有向无环图 1<=n<=5∗1040<=relations.length<=min(n∗(n−1)/2,5∗104)relations[j].length==21<=prevCoursej,nextCoursej<=nprevCoursej!=nextCoursej所有的先修课程对[prevCoursej,nextCoursej]都是互不相同的。time.length==n1<=time[i]<=104先修课程图是一个有向无环图
分析
该问题的复杂性并不大,是最简单的拓扑问题。
就是必须要有一个固定的顺序来依次的访问,每个课程。问题中也提到不会存在环,而且是一个有向无环图。
同时可以同时学习多门课程,相比较之前的一个问题中,要求一个学期只能选k个课程,条件更加宽松。
所以按照拓扑排序的思路来处理,就是需要构建一个图,图无非就是邻接表或者是邻接矩阵。
但是由于问题的规模限制,邻接表是一个比较合适的选择。
然后进行拓扑排序,同时用 f [ i ] f[i] f[i] 记录到达课程i时的最晚时间,而目标是完成所有课程的时候,需要的最少时间,所以要用 a n s ans ans记录每个课程的最晚结束时间。
时间复杂度 O ( M + N ) O(M+N) O(M+N)
空间复杂度 O ( M + N ) O(M+N) O(M+N)
代码
拓扑
class Solution {public int minimumTime(int n, int[][] relations, int[] time) {int[] indeg = new int[n+1];List<Integer>[] g = new ArrayList[n+1];for(int i=1;i<=n;i++){g[i] = new ArrayList();}for(int[] re: relations){int from = re[0],to = re[1];indeg[to]++;g[from].add(to);} Queue<Integer> queue = new LinkedList();for(int i=1;i<=n;i++){if(indeg[i]>0) continue;queue.offer(i);}int[] f = new int[n+1];int ans =0;while(!queue.isEmpty()){int idx = queue.poll(); int end = f[idx]+ time[idx-1];ans = Math.max(ans,end);for(int nx: g[idx]){f[nx]= Math.max(f[nx],end);indeg[nx]--;if(indeg[nx]==0){queue.offer(nx);}}} return ans;}
}
时间复杂度 O ( M + N ) O(M+N) O(M+N)
空间复杂度 O ( M + N ) O(M+N) O(M+N)
Tag
Array
Graph
Topological Sort
相关文章:

【LeetCode 算法】Parallel Courses III 并行课程 III-拓扑
文章目录 Parallel Courses III 并行课程 III问题描述:分析代码拓扑 Tag Parallel Courses III 并行课程 III 问题描述: 给你一个整数 n ,表示有 n 节课,课程编号从 1 到 n 。同时给你一个二维整数数组 relations ,其…...

进行消息撤回功能的测试时,需要考虑哪些?
进行消息撤回功能的测试时,可以考虑以下测试点: 1. 功能可用性测试:确认消息撤回功能是否能够正常使用,并且在不同的场景下(例如单聊、群聊)是否表现一致。 2. 撤回时限测试:检查消息撤回的时…...
C语言动态内存管理(三)
目录 五、C/C程序的内存开辟1.图解2.关键点 六、柔性数组1.什么是柔性数组2.两种语法形式3.柔性数组的特点4.柔性数组的创建及使用在这个方案中柔性数组的柔性怎么体现出来的? 5.不用柔性数组,实现数组可大可小的思路6.对比 总结 五、C/C程序的内存开辟 1.图解 &a…...
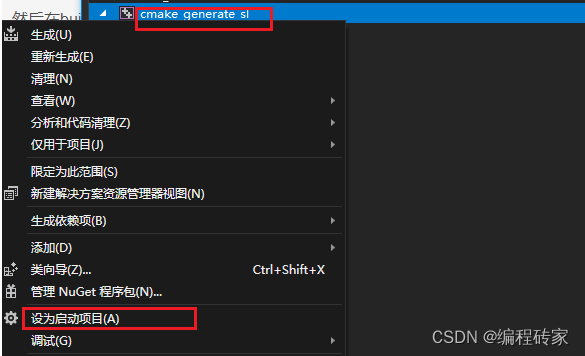
通过cmake工程生成visual studio解决方案
1、前言 visual studio是一个很强大的开发工具,这个工具主要是通过解决方案对我们的源码进行编译等操作。但是我们很多时候拿到的可能并不是一个直接的解决方案,可能是是一个cmake工程,那么这个时候我们就需要通过cmake工程生成解决方案&…...
STM32CubeMX配置STM32G031多通道ADC + DMA采集(HAL库开发)
时钟配置HSI主频配置64M 勾选打开8个通道的ADC 使能连续转换模式 添加DMA DMA模式选择循环模式 使能DMA连续请求 采样时间配置160.5 转换次数为8 配置好8次转换的顺序 配置好串口,选择异步模式配置好需要的开发环境并获取代码 修改main.c 串口重定向 #include &…...
Vue入门项目——WebApi
Vue入门——WebApi vue3项目搭建组合式API响应式APIreactive()ref() 生命周期钩子computed计算属性函数watch监听函数父子通信模板引用组合选项 vue3项目搭建 简单看下Vue3的优势吧 下载安装npm及node.js16.0以上版本(确保安装成功可用如下代码检查版本࿰…...

【电源专题】电量计参数RSOC/RM/FCC定义
在文章【电源芯片】电量计(Gauge)介绍中我们讲到电量计的功能就是监测电池、计量电量。 那么电量计其实也是有很多算法的,比如【电源专题】电量计估计电池荷电状态方法(开路电压法及库仑计法)的差别文章所说的开路电压法和库仑计法。当然还有如阻抗跟踪法、CEDV算法等。 …...

实际开发中,React应用常见问题【持续更新中】
实际开发中,React应用常见问题【持续更新中】 实际开发中,React应用常见问题【持续更新中】 一、路由相关 “react-router-dom”: “^6.14.2”, “react”: “^18.2.0”, 1、监听路由 import { useLocation } from react-router-domexport default func…...

HTML5前端开发工程师的岗位职责说明(合集)
HTML5前端开发工程师的岗位职责说明1 职责 1、根据产品设计文档和视觉文件,利用HTML5相关技术开发移动平台的web前端页面; 2、基于HTML5.0标准进行页面制作,编写可复用的用户界面组件; 3、持续的优化前端体验和页面响应速度,并保证兼容性和…...

Go编写服务监管程序
前言 程序的目的:一个基于Linux系统下的进程监控与管理工具,它能够监控指定的进程或服务的运行情况,并在发现它们不存在或出现异常时自动进行重启操作。这个程序就像一个可靠的看门狗,时刻守护着系统的稳定运行。 程序的本身是周期…...

API商品详情:详尽呈现产品信息的利器
API商品详情:详尽呈现产品信息的利器 随着电子商务的迅速发展,越来越多的企业和开发者开始关注和利用API来实现灵活、高效的商品展示和推广。而在这一领域中,API商品详情成为了无可替代的利器,为用户提供了极为详尽的产品信息。 …...

Cisco 路由器配置管理
大多数网络中断的最常见原因是错误的配置更改。对网络设备配置的每一次更改都伴随着造成网络中断、安全问题甚至性能下降的风险。计划外更改使网络容易受到意外中断的影响。 Network Configuration Manager 网络更改和配置管理 (NCCM)解决方案ÿ…...

java面试真题附参考答案【下册】
tips:下面简述题为java面试真题,阅读本文且感兴趣的,还有将要面试的小伙伴有条件的准备一下笔和纸,将之转述出来成为自己的知识,希望接下来的面试好运连连 上一册:java面试真题【上册】_CsDn.FF的博客-CSD…...

2023牛客多校第三场 B.Auspiciousness
传送门 前题提要:没得说,赛时根本没想到dp,赛后翻各大题解看了很久,终于懂了dp的做法,故准备写一篇题解. 首先,先定义一下我们的 d p dp dp方程,考虑将处于 [ 1 , n ] [1,n] [1,n]的数当做小数,将处于 [ n 1 , 2 ∗ n ] [n1,2*n] [n1,2∗n]的数当做大数.那么对于我们的摸牌结…...

Numpy—数组的分隔与转置
⛳数组的切分 split 分隔 numpy.split 函数沿特定 的轴将数组分割为子数组,格式如下: numpy.split(ary, indices_or_sections, axis)参数说明: arry:被分割的数组。indices_or_sections:如果是一个整数,就…...

PyTorch中级教程:深入理解自动求导和优化
在你已经掌握了如何使用PyTorch构建神经网络的基础上,接下来我们将深入探讨PyTorch的两个核心特性:自动求导(Autograd)和优化(Optimization)。这两个特性在深度学习模型的训练过程中起着至关重要的作用。 …...
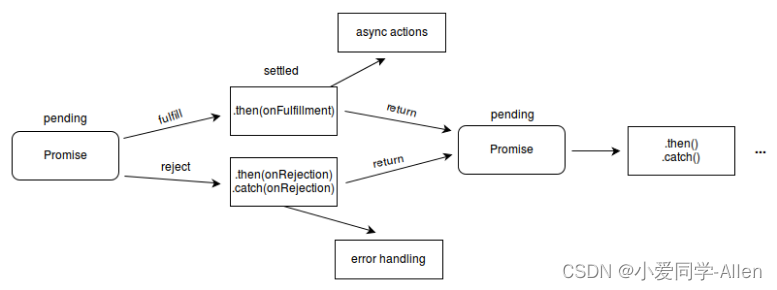
ES6基础知识六:你是怎么理解ES6中 Promise的?使用场景?
一、介绍 Promise,译为承诺,是异步编程的一种解决方案,比传统的解决方案(回调函数)更加合理和更加强大 在以往我们如果处理多层异步操作,我们往往会像下面那样编写我们的代码 doSomething(function(resu…...
函数,格式(CAST AS decimal))
数据库CAST()函数,格式(CAST AS decimal)
语法: CAST (expression AS data_type) 参数说明: expression:任何有效的SQServer表达式。 AS:用于分隔两个参数,在AS之前的是要处理的数据,在AS之后是要转换的数据类型。 data_type:目标系统…...

LRU 缓存结构
文章目录 LRU实现 LRU 优先去除最久没有访问到的数据。 实现 通过组合哈希表(Hash Table)和双向链表(Doubly Linked List)实现 LRU 缓存。并且以 O(1) 的时间复杂度执行 get 和 put 操作核心是对节点的新增、访问都会让节点移动…...
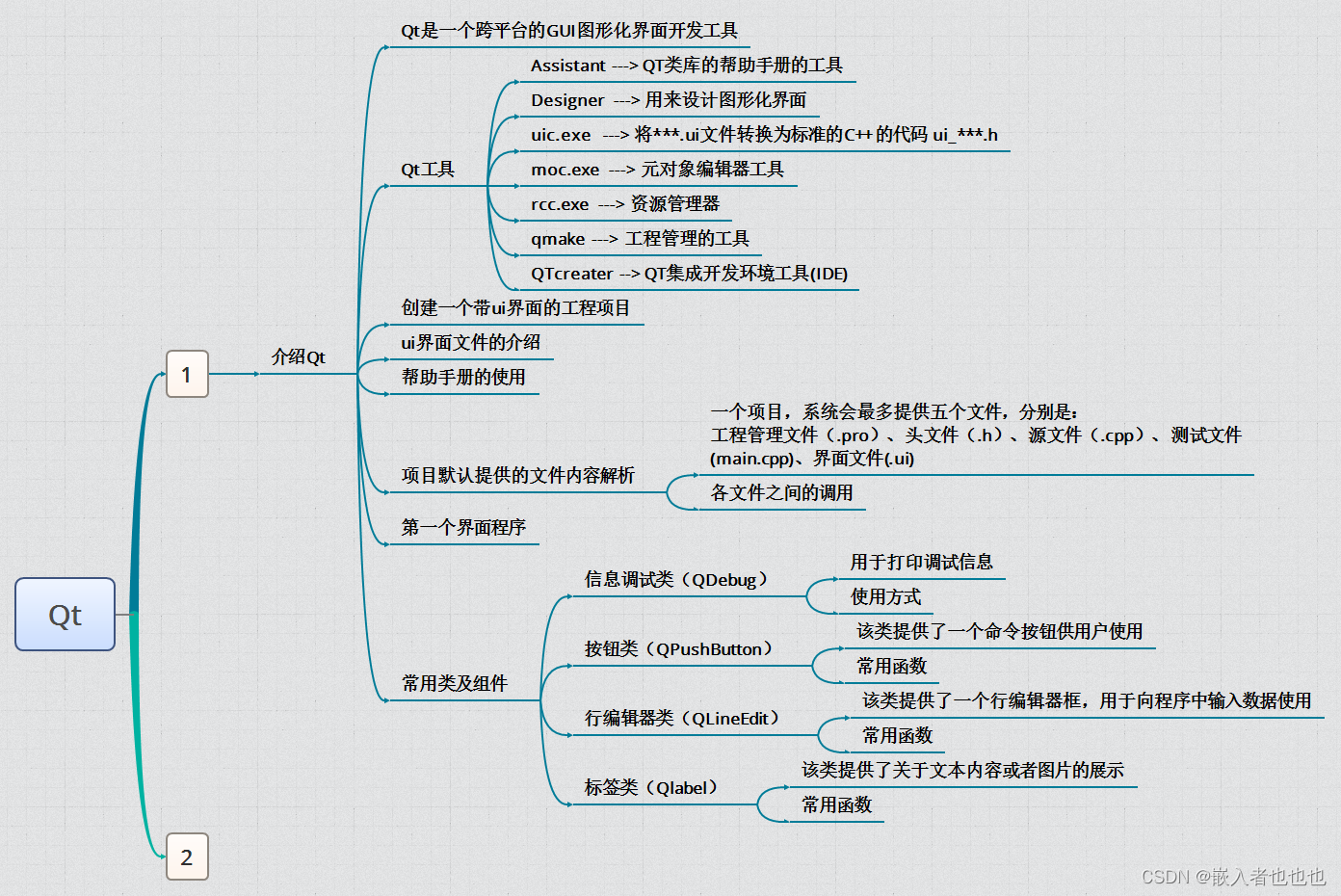
DAY1,Qt [ 手动实现登录框(信息调试类,按钮类,行编辑器类,标签类的使用)]
1.手动实现登录框; ---mychat.h---头文件 #ifndef MYCHAT_H #define MYCHAT_H#include <QWidget> #include <QDebug> //打印信息 #include <QIcon> //图标 #include <QPushButton> //按钮 #include <QLineEdit> //行编辑器类 #in…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
