2023牛客多校第三场 B.Auspiciousness
传送门
前题提要:没得说,赛时根本没想到dp,赛后翻各大题解看了很久,终于懂了dp的做法,故准备写一篇题解.
首先,先定义一下我们的 d p dp dp方程,考虑将处于 [ 1 , n ] [1,n] [1,n]的数当做小数,将处于 [ n + 1 , 2 ∗ n ] [n+1,2*n] [n+1,2∗n]的数当做大数.那么对于我们的摸牌结果来说,必然是小数的递增序列+大数的下降序列相交换的形式(例如n=5,[1,2,3,7,6])
那么我们可以得出一个 d p dp dp方程,我们设 d p [ i ] [ j ] [ 0 / 1 ] dp[i][j][0/1] dp[i][j][0/1]当前摸到的牌中有 i i i段是小数序列,有 j j j段是大数序列,并且最后一段是大数/小数序列(0代表小数,1代表大数)的方案数.
此时考虑递推,对于每一个 [ i , j ] [i,j] [i,j]的状态,都可以通过上一次摸牌转移过来:
d p [ i ] [ j ] [ 0 ] = ∑ k = 1 i d p [ i − k ] [ j ] [ 1 ] ∗ C [ n − ( i − k ) ] [ k ] dp[i][j][0]=\sum_{k=1}^{i}dp[i-k][j][1]*C[n-(i-k)][k] dp[i][j][0]=k=1∑idp[i−k][j][1]∗C[n−(i−k)][k]简单解释一下上述的递推式的意义.对于当前的状态,如果最后是小数序列,那么因为整个是大数与小数相交换的,所以上一次的状态必然是大数状态,并且此时我们从小数的堆中挑了 k k k个数加入到我们的手牌中,因为上一次状态小数的总个数是 n − ( i − k ) n-(i-k) n−(i−k),所以不难使用组合数得出上式.
类似的我们有:
d [ i ] [ j ] [ 1 ] = ∑ k = 1 j d p [ i ] [ j − k ] [ 0 ] ∗ C [ n − ( j − k ) ] [ k ] d[i][j][1]=\sum_{k=1}^{j}dp[i][j-k][0]*C[n-(j-k)][k] d[i][j][1]=k=1∑jdp[i][j−k][0]∗C[n−(j−k)][k]显然的,上面的递推式并没有完全解决我们的问题.因为我们的问题是总的摸牌数.上面求出的单单只是当前摸到某个状态的牌的方案数.那么对于每一次摸牌的结果,也就是每一个 d p [ i ] [ j ] [ 0 / 1 ] dp[i][j][0/1] dp[i][j][0/1]的状态,其实都是我们的答案.想象一下每一次状态其实我们都可以是一次技能的结束,也就是每一次状态我们都可能都止步于此.那么此时我们需要考虑的就是对于每一个状态我们停止的方案数.因为显然的,每一个状态我们有可能停止也有可能继续

考虑如上图的状态(分成三段),也就是 ( i + j − k − > i + j ) (i+j-k->i+j) (i+j−k−>i+j)产生的方案数.不妨假设我们摸的 k k k是小数序列(大数与之类似)
因为我们需要恰好在摸完 k k k之后停止,那么说明我们的 k k k并不是一个完全递增序列,也就是最后一张牌比前面那张小.那么此时我们只有 k − 1 k-1 k−1中方案.就比如摸到了 1 , 2 , 3 , 4 1,2,3,4 1,2,3,4,那么此时会停止的状态只有 1 , 2 , 4 , 3 ∣ 1 , 3 , 4 , 2 ∣ 2 , 3 , 4 , 1 1,2,4,3\;|\;1,3,4,2\;|\;2,3,4,1 1,2,4,3∣1,3,4,2∣2,3,4,1(注意我们除了最后一位需要保证递增,因为需要保证摸完k张牌).并且此时对于后面的所有剩下来的 2 n − i − j 2n-i-j 2n−i−j张没摸的牌来说,此时是可以随意摆放的(注意,我们是最终是所有的可能性的总和,所以即使牌没摸,但是不同摆放依旧算一种).所以此时的方案数乘上 ( 2 n − i − j ) ! (2n-i-j)! (2n−i−j)!.然后我们需要的是总的摸牌数,那么对于每一个状态,我们都乘上该状态摸到的牌数,也就是 i + j i+j i+j
所以此时的方案数就是(状态是 [ i , j , 0 ] [i,j,0] [i,j,0]): d p [ i − k ] [ j ] [ 1 ] ∗ c [ n − ( i − k ) ] [ k ] ∗ ( k − 1 ) ∗ f a c [ 2 ∗ n − ( i + j ) ] ∗ ( i + j ) dp[i-k][j][1]*c[n-(i-k)][k]*(k-1)*fac[2*n-(i+j)]*(i+j) dp[i−k][j][1]∗c[n−(i−k)][k]∗(k−1)∗fac[2∗n−(i+j)]∗(i+j)类似的,假如最后的序列是大数,那么方案数就是(状态是 [ i , j , 1 ] [i,j,1] [i,j,1]): d p [ i ] [ j − k ] [ 0 ] ∗ c [ n − ( j − k ) ] [ k ] ∗ ( k − 1 ) ∗ f a c [ 2 ∗ n − ( i + j ) ] ∗ ( i + j ) dp[i][j-k][0]*c[n-(j-k)][k]*(k-1)*fac[2*n-(i+j)]*(i+j) dp[i][j−k][0]∗c[n−(j−k)][k]∗(k−1)∗fac[2∗n−(i+j)]∗(i+j)
因为模数不确定,也就是不一定是素数,可能没有逆元,所以需要预处理组合数
至此,本题结束
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
inline void print(__int128 x){if(x<0) {putchar('-');x=-x;}if(x>9) print(x/10);putchar(x%10+'0');
}
#define maxn 1000000
#define int long long
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int c[610][610];int n,mod;int fac[maxn];
int dp[610][610][2];//i个小数,j个大数,k=0代表末尾小,1代表末尾大
void init() {for(int i=0;i<=2*n;i++) {for(int j=0;j<=2*n;j++) {dp[i][j][0]=dp[i][j][1]=0;}}c[0][0]=1;for(int i=1;i<=2*n;i++) {c[i][0]=1;for(int j=1;j<=i;j++){c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;}}fac[0]=1;for(int i=1;i<=2*n;i++) fac[i]=fac[i-1]*i%mod;
}
signed main() {int T=read();while(T--) {n=read();mod=read();init();int ans=0;dp[0][0][0]=dp[0][0][1]=1;for(int i=0;i<=n;i++) {for(int j=0;j<=n;j++) {for(int k=1;k<=i;k++) {dp[i][j][0]+=dp[i-k][j][1]*c[n-(i-k)][k]%mod;dp[i][j][0]%=mod;ans+=dp[i-k][j][1]*c[n-(i-k)][k]%mod*(k-1)%mod*fac[2*n-(i+j)]%mod*(i+j)%mod;ans%=mod;}for(int k=1;k<=j;k++) {dp[i][j][1]+=dp[i][j-k][0]*c[n-(j-k)][k]%mod;dp[i][j][1]%=mod;ans+=dp[i][j-k][0]*c[n-(j-k)][k]%mod*(k-1)%mod*fac[2*n-(i+j)]%mod*(i+j)%mod;ans%=mod;}}}ans+=(dp[n][n][0]+dp[n][n][1])%mod*2*n%mod;ans%=mod;cout<<ans<<endl;}return 0;
}
相关文章:

2023牛客多校第三场 B.Auspiciousness
传送门 前题提要:没得说,赛时根本没想到dp,赛后翻各大题解看了很久,终于懂了dp的做法,故准备写一篇题解. 首先,先定义一下我们的 d p dp dp方程,考虑将处于 [ 1 , n ] [1,n] [1,n]的数当做小数,将处于 [ n 1 , 2 ∗ n ] [n1,2*n] [n1,2∗n]的数当做大数.那么对于我们的摸牌结…...

Numpy—数组的分隔与转置
⛳数组的切分 split 分隔 numpy.split 函数沿特定 的轴将数组分割为子数组,格式如下: numpy.split(ary, indices_or_sections, axis)参数说明: arry:被分割的数组。indices_or_sections:如果是一个整数,就…...

PyTorch中级教程:深入理解自动求导和优化
在你已经掌握了如何使用PyTorch构建神经网络的基础上,接下来我们将深入探讨PyTorch的两个核心特性:自动求导(Autograd)和优化(Optimization)。这两个特性在深度学习模型的训练过程中起着至关重要的作用。 …...
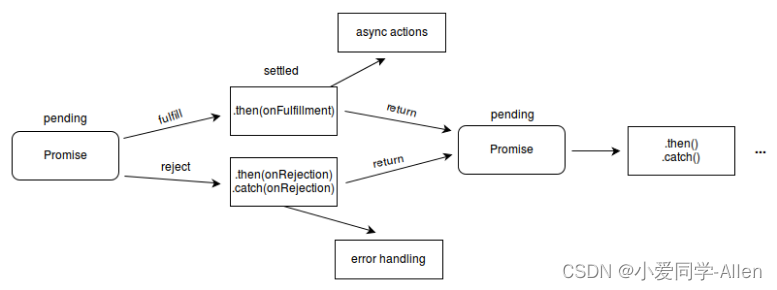
ES6基础知识六:你是怎么理解ES6中 Promise的?使用场景?
一、介绍 Promise,译为承诺,是异步编程的一种解决方案,比传统的解决方案(回调函数)更加合理和更加强大 在以往我们如果处理多层异步操作,我们往往会像下面那样编写我们的代码 doSomething(function(resu…...
函数,格式(CAST AS decimal))
数据库CAST()函数,格式(CAST AS decimal)
语法: CAST (expression AS data_type) 参数说明: expression:任何有效的SQServer表达式。 AS:用于分隔两个参数,在AS之前的是要处理的数据,在AS之后是要转换的数据类型。 data_type:目标系统…...

LRU 缓存结构
文章目录 LRU实现 LRU 优先去除最久没有访问到的数据。 实现 通过组合哈希表(Hash Table)和双向链表(Doubly Linked List)实现 LRU 缓存。并且以 O(1) 的时间复杂度执行 get 和 put 操作核心是对节点的新增、访问都会让节点移动…...
DAY1,Qt [ 手动实现登录框(信息调试类,按钮类,行编辑器类,标签类的使用)]
1.手动实现登录框; ---mychat.h---头文件 #ifndef MYCHAT_H #define MYCHAT_H#include <QWidget> #include <QDebug> //打印信息 #include <QIcon> //图标 #include <QPushButton> //按钮 #include <QLineEdit> //行编辑器类 #in…...

25.8 matlab里面的10中优化方法介绍—— 拉各朗日乘子法求最优化解(matlab程序)
1.简述 拉格朗日乘子法: 拉格朗日乘子法(Lagrange multipliers)是一种寻找多元函数在一组约束下的极值的方法。通过引入拉格朗日乘子,可将有 变量与 约束条件的最优化问题转化为具有变量的无约束优化问题求解 举个例子ÿ…...

2023年自然语言处理与信息检索国际会议(ECNLPIR 2023) | EI Compendex, Scopus双检索
会议简介 Brief Introduction 2023年自然语言处理与信息检索国际会议(ECNLPIR 2023) 会议时间:2023年9月22日-24日 召开地点:中国杭州 大会官网:ECNLPIR 2023-2023 Eurasian Conference on Natural Language Processing and Information Retr…...

Python - 嵌入式数据库Sqlite3的基本使用
SQLite是一种轻量级的嵌入式关系型数据库管理系统,而Python标准库中提供了与SQLite交互的模块,sqlite3。下面是一个Python 3中使用sqlite3模块的详细示例与解析。 import sqlite3 # 创建或连接数据库 conn sqlite3.connect(example.db) # 创建一个…...

VB制作网页自动填表
VB制作简单模拟器教程入门版 第一讲 如何用VB编程打开一个网页: 由于是为做模拟器做铺垫,所以就不介绍别的方法,只介绍一种最简单的用webbrowser控件实现(实际是其他的方法我还没有学会)。 下面我们就开始步入模…...

Kotlin 和 Java对比,具体代码分析
目录 一、语法比较二、案列分析 Kotlin 和 Java 都是广泛使用的编程语言,它们有一些共同点,例如都追求面向对象编程,但也有许多不同之处。下面是 Kotlin 和 Java 之间的一些比较: 一、语法比较 声明变量:Kotlin 使用 …...
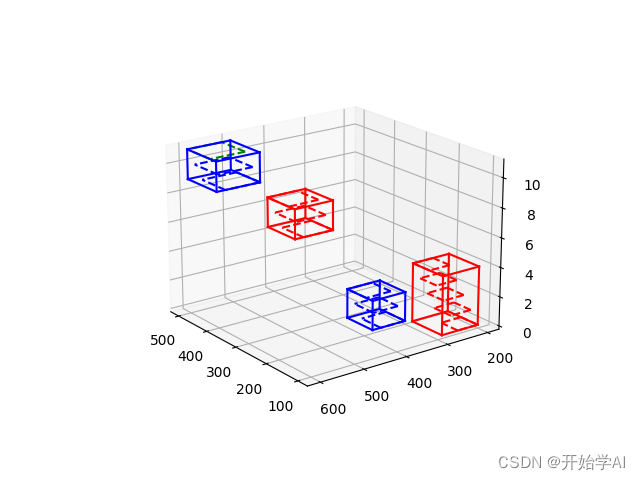
目标检测之3维合成
现在有一系列的图片,图片之间可以按照z轴方向进行排列。图片经过了目标检测,输出了一系列的检测框,现在的需求是将检测框按类别进行合成,以在3维上生成检测结果。 思路:将图片按照z轴方向排列,以z轴索引作…...

【playbook】Ansible的脚本----playbook剧本
Ansible的脚本----playbook剧本 1.playbook剧本组成2.playbook剧本实战演练2.1 实战演练一:给被管理主机安装Apache服务2.2 实战演练二:使用sudo命令将远程主机的普通用户提权为root用户2.3 实战演练三:when条件判断指定的IP地址2.4 实战演练…...

PySpark基本操作:如何查看源码
方法一: from pyspark.mllib.tree import GradientBoostedTrees import inspectsource_code inspect.getsource(GradientBoostedTrees) print(source_code) 方法二: GradientBoostedTrees — PySpark 3.4.1 documentation (apache.org) 在官网中&…...

HCIP——OSPF的防环机制
OSPF的防环机制 一、域间防环二、域内防环有向图转化1、有向图的画法2、示例: 三、SPF算法 OSPF将整个OSPF域划分为多个区域,区域内部通过拓扑信息计算路由,区域间传递路由信息,实现全网可达。OSPF防环机制主要是体现在域内防环和…...

安全基础 --- 正则表达式
正则表达式是表达文本模式的方法 正则表达式(Regular Expression),简称为正则或Regex,是一个用来描述、匹配和操作字符串的工具。 (1)限定字符 限定字符多用于重复匹配次数 常用限定字符: 语…...

【vue】vue面试高频问题之-$nextTick的作用和使用场景
nextTick的作用和使用场景 vue中的nextTick主要用于处理数据动态变化后,DOM还未及时更新的问题,用nextTick就可以获取数据更新后最新DOM的变化 api文档 Vue.nextTick( [callback, context] ) 参数: {Function} [callback]{Object} [context]…...

MySQL学习笔记之SQL语句执行过程查看
文章目录 参数使能查看最近一条SQL执行过程查看profiling打开开后,所有SQL语句执行耗时查看某一条SQL的执行过程指定要查看的性能选项查看所有性能选项 参数使能 以select语句为例,首先打开profile参数: mysql> set profiling 1; Query…...
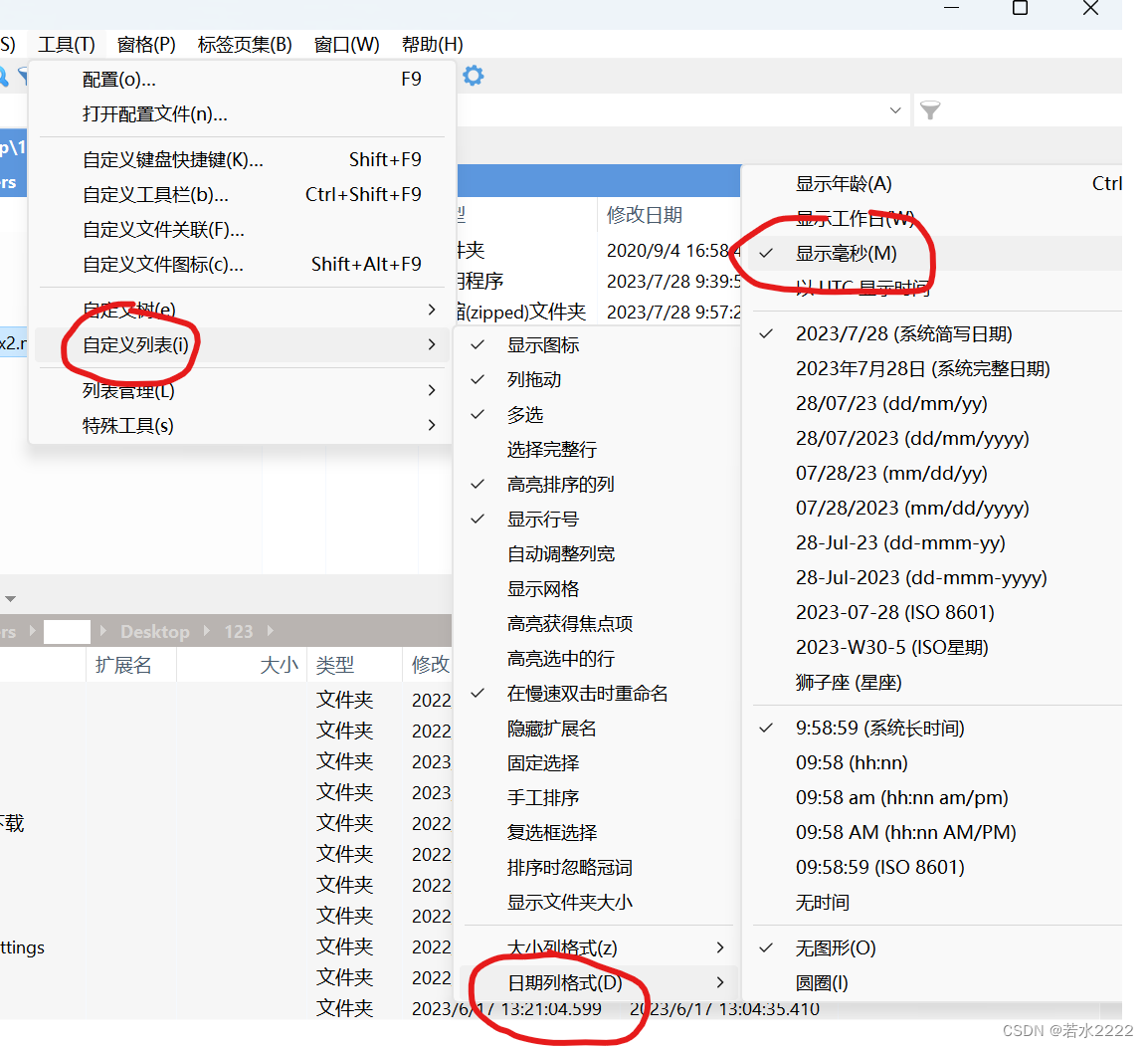
如何以毫秒精度,查看系统时间以及文件的创建时间
用 cmd 查看系统的时间: powershell -command "(Get-Date -UFormat %Y-%m-%d %H:%M:%S).toString() . ((Get-Date).millisecond)" 用 XYplorer 查看文件的精确创建时间(含30天试用): XYplorer - File Manager for …...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

codeforces C. Cool Partition
目录 题目简述: 思路: 总代码: https://codeforces.com/contest/2117/problem/C 题目简述: 给定一个整数数组,现要求你对数组进行分割,但需满足条件:前一个子数组中的值必须在后一个子数组中…...
